Central zero-triangles in rotationally symmetrical XOR-Triangles.
Michael Thomas De Vlieger, St. Louis, Missouri. 2020 0512.
Abstract:
We discuss and analyze rotationally symmetrical XOR-triangles (RSTs) that have central zero-triangles (CZTs), determining two key metrics (side length k, frame width j). Methods of quantification of zero triangles are outlined, and linear recurrences that generate RSTs with CZTs of a given frame width are given, acoompanied by linked charts, Mathematica code, and tables. This work builds on OEIS A334556 authored by Peter Kagey and originally posed at MathOverflow [1], posing several new sequences in the OEIS.
1. The XOR-triangle.
The exclusive-or or XOR has a simple truth table: if both binary inputs agree, the result is false, else true. In terms of bits, XOR yields 0 if its inputs are both {0, 0} or both {1, 1}, otherwise 1.
We produce an XOR-triangle T(n) given a number n, converted to binary b(n) to obtain ℓ = 1 + ⌊log2 n⌋ binary digits or bits. (More precisely, ℓ = A070939(n), as ℓ(0) = 1.) Taking adjacent pairs of bits as input, XOR converts them to a new, child bit to form a new number in iteration m = 1. We employ the output of iteration m as input for iteration (m + 1) until left with a single bit, since each iteration reduces the bit-length by 1 (i.e., bit-length = ℓ – m + 1). Therefore we end up with (ℓ − 1) iterations ℓ (i.e., 1 ≤ m < ℓ). The results from each iteration, taken together as bits, forms the XOR-triangle.
Example: For n = 11, we have b(11) = 10112. We apply the recursive function to 10112 and in each iteration we have 1011 ⇒ 110 ⇒ 01 ⇒ 1. Code 1.1 generates the bits in each iteration. Code 1.3 produces a diagram as seen in Figure 1.1.
We might arrange the bits thus:
1 0 1 1
1 1 0
0 1
1
thereby forming a triangle, hence, an XOR triangle. Figure 1.1 below shows a diagrammatic representation of T(11), a 4-bit number, using filled circles to represent 1s, and empty or hollow circles to represent 0s.
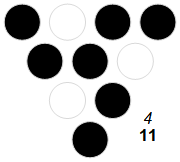
The diagrams aid in visually examining patterns in the XOR-triangles. Furthermore, the diagrams exhibit the symmetry that is the subject of this paper, beyond merely being aesthetically pleasant, directing our study.
Figure 1.2 diagrams XOR triangles T(n) for 1 ≤ n ≤ 96, replacing 1 or “on” bits as filled circles, and 0 or “off” bits as hollow (i.e., white-filled) circles. Among these, we note rotational symmetry in the darker diagrams for n = {1, 11, 39, 57, 83, 91, …}. (Click for a higher resolution small chart, and a large chart showing XOR triangles T(n) for n ≤ 1024).
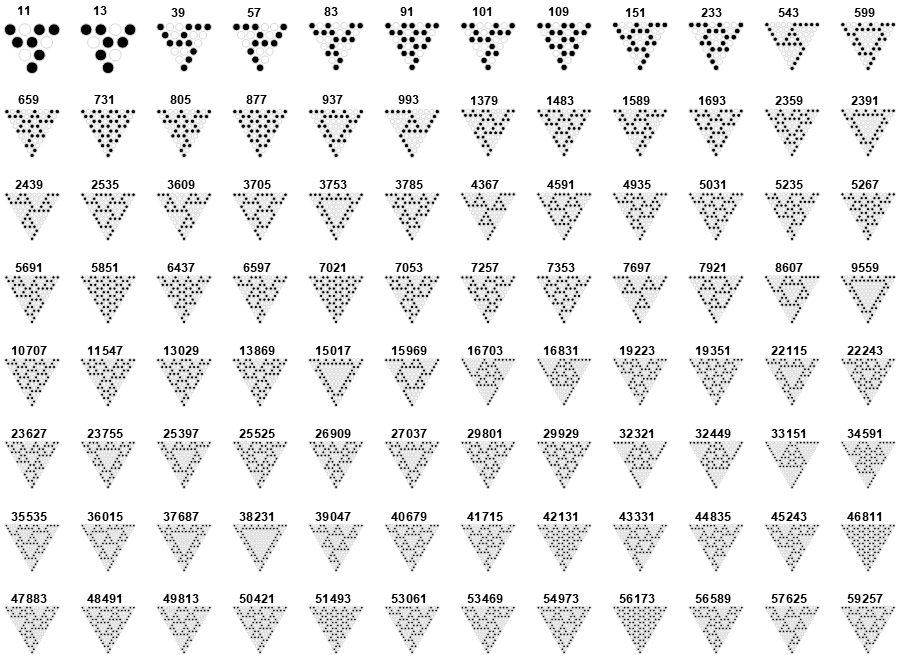
These numbers have an interesting layout as shown in Figure 1.3, in a table that arranges the natural numbers as {{1}, {2, 3}, {4, 5, 6, 7}, {8, 9, 10, 11, 12, 13, 14, 15}, {16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31}, …}.

From this layout we derive the sequence A334796: {2, 0, 0, 2, 0, 2, 4, 2, 0, 8, 4, 8, 16, 8, 16, 32, 0, 32, 64, 32, 64, 128, …}.
Relation of XOR-triangles with Sierpiński’s and Pascal’s Triangles.
The XOR-triangle is related to the Sierpiński Triangle, or, more precisely, Pascal’s Triangle (mod 2) [2][3]. It is less related to elementary cellular automaton rules that require three inputs to yield one output for an eightfold truth table, furnishing a pattern in a rectangular arrangement. Furthermore, the cellular automaton (usually) interprets negative space as input. Each cell in one iteration influences three subsequent output cells, whereas the XOR-triangle strictly requires 2 inputs to yield one output and does not take negative space into account. The elementary cellular automaton rules most closely related to the XOR-triangle are rules 30, 60, and 90.
We generate Pascal’s Triangle (mod 2) from a single 1-bit, allowing new bits to be created from a single input bit, whereas in the XOR-triangle, we require two bits for input. Hence, the lengths increment for each iteration in Pascal’s Triangle, making for an infinite fractal, having been generated from a single point, while in the XOR-triangle, subsequent iterations decrement till we end up with a single bit, a finite structure sensitive to the seed b(n).
Figure 1.4 below compares Pascal’s Triangle (mod 2), generated from a single 1-bit, carried out to include 26 − 1 generations, left, with an XOR-triangle T(1021310428437572697), generated by a 60-bit seed number (hexadecimal e2c6c6c6c6c6c59) at right. This seed produces a rotationally-symmetrical XOR-triangle (RST) that features a central zero triangle (CZT).
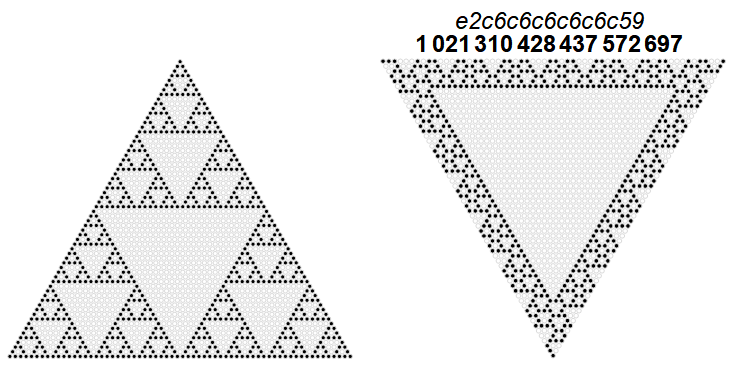
2. Rotationally symmetrical XOR-triangles (RSTs).
In the above chart, we can see that there are many odd n (i.e., binary palindromes, A006995 = {1, 3, 5, 7, 9, 15, 17, 21, 27, 31, 33, 45, 51, 63, 65, 73, 85, 93, 99, 107, 119, …}) that are translationally symmetrical, meaning that we can flip or reverse them horizontally and have an identical arrangement. As these are generated by palindromic bitstrings, we may dispense with the notion of XOR-triangles, and the question is not interesting. Rémy Sigrist posed A334918, which includes any XOR-triangle that features reflective symmetry across any angle (see this montage).
A more interesting question regards rotationally symmetrical XOR-triangles. These maintain the same appearance under rotation. We find that the only XOR-triangle that is both rotationally and translationally symmetrical is T(1).
We can test T(n) to determine if it is rotationally symmetrical by padding each iteration m so as to have a list of length ℓ = A070939(n). Example: given T(11) = 1011 ⇒ 110 ⇒ 01 ⇒ 1, instead of producing an equilateral arrangement, we render it as a left-justified “dog-ear” shape:
1 0 1 1
1 1 0
0 1
1
Then we fill out the rows with a value (like −1) to have length ℓ:
1 0 1 1
1 1 0 −1
0 1 −1 −1
1 −1 −1 −1
Once rotated, we extract the padding, then we can compare T '(n) with T(n); if identical, then we have a rotationally symmetrical XOR triangle.
Sequence A334556 (author Peter Kagey) lists numbers n whose binary expansion b(n) produces an XOR-triangle that is rotationally symmetrical (RST). In this sequence, we note the appearance of both a number n and its binary integer-reverse n′ = A030101(n). meaning that the bits of b(n) appear reversed in n′.
We can generate A334556 using Code 1.2.
Figure 2.1 shows terms 2 ≤ n ≤ 97 of A334556. Click for a higher resolution small chart, and a fuller chart of terms 2 ≤ n ≤ 1354

The binary weight of these figures includes the numbers {1, 7, 12, 16, 19, 21, 24, 30, 31, 36, 37, 39, 40, …}, i.e., numbers congruent to 0 or 1 (mod 3) exclusive of a perhaps-finite pair of lists 3k with k = {1, 2, 3, 5, 6, 9, 11, 17, 27, …}, and 3j + 1 with j = {1, 3, 4, 7, 8, 9, 11, 14, 15, 18, 19, 21, 23, 25, 27, 28, 39, 41, 43, 45, …} (though j and k may be a finite list).
3. Zero-triangles.
Let’s define the zero-triangle or ZT with side length k as a run of 0s in iteration m that emerge due to a run of (k + 1) 1s in a preceding iteration (m – 1). By definition of binary, each run of a given parity is delimited by a bit of reverse parity, therefore runs are bordered by opposite parity. Following from the definition of XOR, pair agreement produces a zero, a run of k 1s produces a run of (k – 1) zeros, therefore we see the emergence of “voids” or “bubbles” of zeros, necessarily tapering and triangular in arrangement, versus same of 1s. Since every child bit in the ensuing iteration is one from agreeing parents, we see a run of k zeros, obviously hemmed in by neighboring and delimiting 1s on either side, forming a solid border. The following iteration (m + 1) features a series of (k – 1) zeros, etc., until the end condition tapers the run of zeros to a single zero flanked by 1s. The iteration after this features adjacent 1s, then a single zero, thus the border of 1s is triangular, but without its vertices. Therefore we have a triangle of zeros bordered by a truncated border of 1s.
The XOR-triangles T(n) produce an assortment of zero-triangles delimited by single-bit-width borders of 1s. Indeed, the occasion of runs of 1s in any direction is temporary, since agreeing bits convert to zeros, and disagreement generates a 1-bit. A singleton 1-bit produces a lineage of 1-bits that perpetuates left or right, giving rise to pairs of 1-bits every other generation (since a pair of 1-bits produces a 0-bit in the intercalated generations) in the direction counter to propagation, maintaining a zero-triangle in the direction of travel until it encounters the border of the ZT. After encounter, the pair of 1-bits are “annihilated”, however, the 1-0 boundary emits a new 1-bit. Therefore, we observe a “lacy” texture of 1-bits that is never more than 1 bit “thick”.
What we are left with are zero-triangle “bubbles” wherein the shells of the bubbles are single-bit-thickness 1s. This pattern is well-known and is akin to the Sierpiński and Pascal triangles (mod 2) as mentioned in Section 1.
We can enumerate ZTs of side length k for T(n) in an irregular triangle S(n, k); this appears at OEIS A333624. (Generate via Code 3.1) The table below shows the first few rows, where we might encode row n using A067255 and thereby obtain a succinct compression:
Table begins: Read S(n, k) as A067255(r)
0; 1
1; 2
1; 2
0, 1; 3
2; 4
2; 4
0, 1; 3
0, 0, 1; 5
1, 1; 6
2, 1; 12
3; 8
2, 1; 12
3; 8
1, 1; 6
0, 0, 1; 5
0, 0, 0, 1; 7
1, 0, 1; 10
3, 1; 24
1, 2; 18
1, 2; 18
2, 0, 1; 20
OEIS A333625 applies the compression mentioned above, interpreting row r = S(r, k) for r in A334556 as row r in A067255. This admits the full dataset available at A334556, processed to produce a row of A333624, as a valid and easily decodable OEIS b-file for A333625.
4. Central zero-triangles (CZTs).
Certain RSTs give rise to a central “bubble” or “void” of zeros, essentially a zero-triangle framed by a rotationally-symmetrical pattern, j bits thick, on all three sides. We can regard RSTs with a central zero-triangle (CZT) as a doubly-special case of the XOR-triangle, a sort of symmetrically-hollow RST. The framing pattern’s bits, adjacent to the CZT are solidly one-bits when the bits are tangent to one of the zeros in the CZT as explained above, as the CZT is just a special case of a zero-triangle. Thus the CZT has side length k and frame width j.
For RSTs, j > 1, since a solid run of ℓ 1s would give rise to a solid run of (ℓ – 1) zeros in iteration m = 2, and every iteration thereafter consists of zeros. Therefore T(2(ℓ – 1) – 1) is not rotationally symmetrical except when ℓ = 1 and T(1) consists of a single 1 bit. Generally,
j = (ℓ – k)/3 = (1 + ⌊log2 n⌋ – k)/3.
Thus the largest possible central zero-triangle is ℓ – 6, or in terms of n, ⌊log2 n⌋ – 5.
Sequence A334769 lists those n that produce RSTs that have a central “bubble” or “void” of zeros. (Generate using Code 4.1) If a number n is in A334769, so is its binary integer-reverse n′ = A030101(n). The numbers n and n′ share the same values of j and k, and entries in A333624, as they are transformationally symmetrical.
Figure 4.1 shows the first 32 terms of A334769. (Click for an image of the smallest 144 terms, or an image of the terms of A334769 accentuated in black amid the terms of A334556 in gray.)
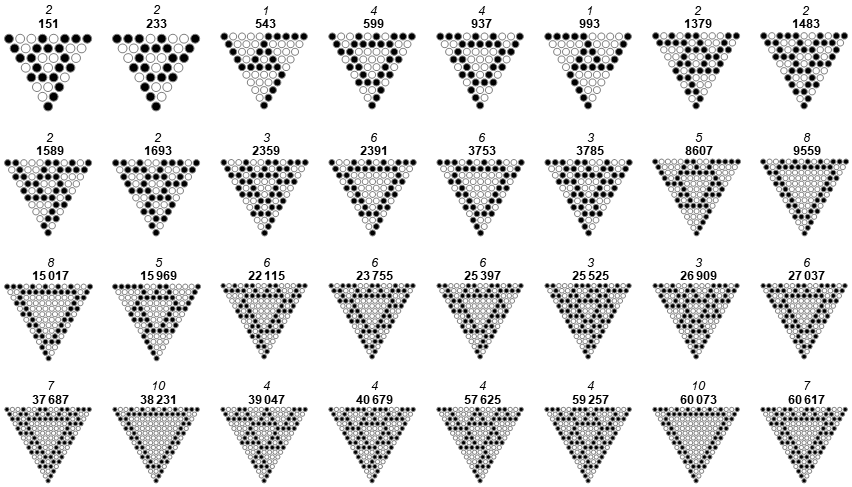
The binary weight of these figures includes the numbers {21, 24, 30, 36, 39, 45, 48, 57, 60, 63, 66, 69, 72, 75, 84, 87, 90, …}, multiples of 3. It is uncertain whether the density of multiples of 3 increases such that eventually, a binary weight with any multiple of 3 can be found in a rotationally symmetrical XOR-triangle that has a central zero triangle.
5. Key Aspects of CZTs of RSTs.
Sequence A334770 shows side length k for the corresponding RST in A334769 (see Code 5.1), while A334796 shows frame width j for same. (See Code 5.2.) Hence, in terms of sequences:
frame width j = A334796(i) = (A070939(A334769(i)) – A334770(i))/3,
with i the index common to both A334769 and A334770.
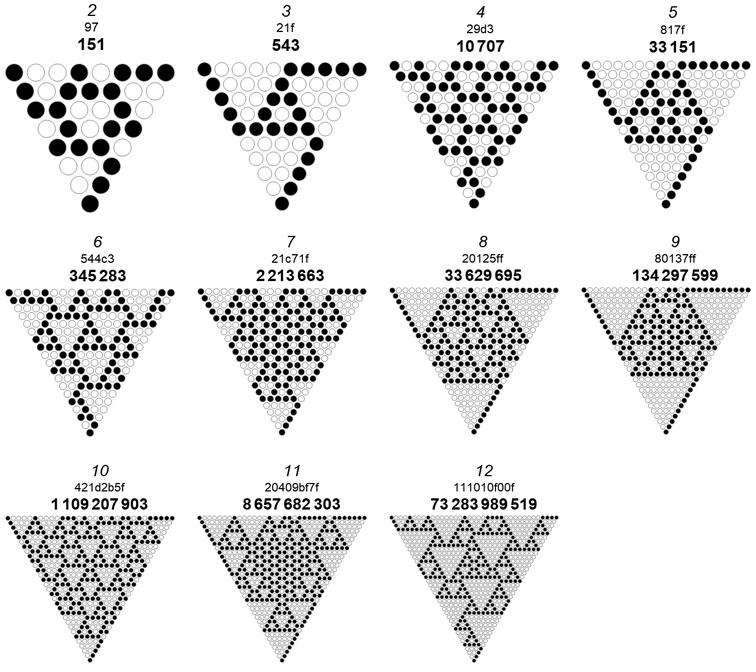
Smallest numbers n that produce RSTs with CZTs with frame width j.
We observe the smallest n with j = {2, 3, 4, 5, …} are {151, 543, 10707, 33151, 88401091, 60262180761} = OEIS A334836.
In the table below, j = frame width, i is the index of the value j in A334796, n generates T(n) with the frame width j, L = A070939(n), and k is the side length of the CZT in T(n), asterisked when n is the first instance of the value k in A334769. Again, we state n in hexadecimal to accentuate the pattern of bits.
j i n n_16 L k
------------------------------------------------
2 1 151 97 8 *2
3 3 543 21f 10 *1
4 17 10707 29d3 14 2
5 31 33151 817f 16 1
6 63 345283 544c3 19 1
7 163 2213663 21c71f 22 1
8 351 33629695 20125ff 26 2
9 607 134297599 80137ff 28 1
10 1407 1109207903 421d2b5f 31 1
11 2415 8657682303 20409bf7f 34 1
12 5471 73283989519 111010f00f 37 1
...
Figure 5.1 shows the smallest instances n of RSTs that generate CZTs with frame width j as noted in italic. (See a dozen smallest instances of 2 ≤ j ≤ 12):
Smallest numbers n that produce RSTs with CZTs of side length k.
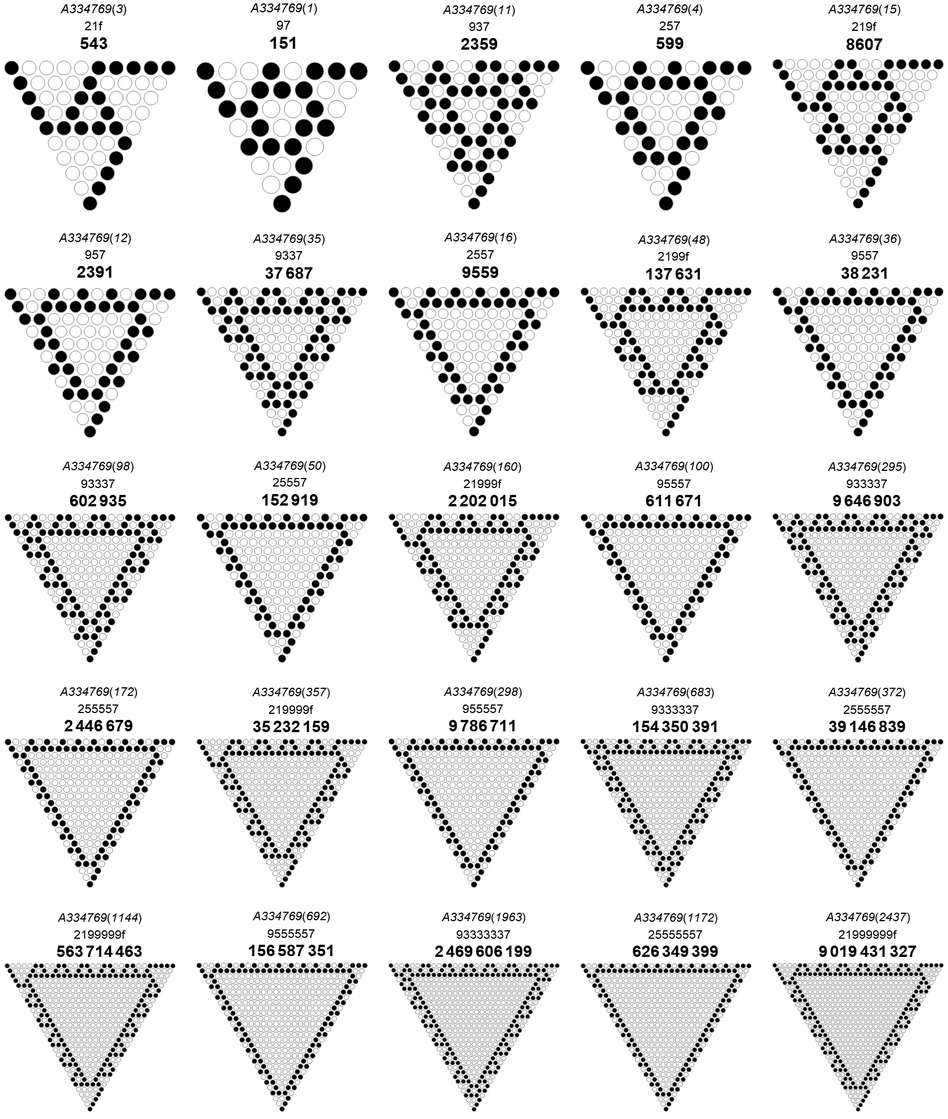
We define A334771 as a list of smallest n that produce an RST with CZT of side length k. (See Code 5.3.) This sequence begins: {543, 151, 2359, 599, 8607, 2391, 37687, 9559…}. The table below shows the smallest n that generate an RST with CZT of side length k, the index i of n in A334769, the index m of n in A334556, n itself and expanded hexadecimally, and the frame width j of the CZT of T(n).
k i m n n_16 j Run Length Recipe
----------------------------------------------------------------------
1 3 12 543 21f 3 145
2 1 10 151 97 2 12113
3 11 24 2359 937 3 1212213
4 4 13 599 257 2 1211113
5 15 48 8607 219f 3 14225
6 12 25 2391 957 2 12..3(11)..3
7 35 76 37687 9337 3 121..2(22)..13
8 16 49 9559 2557 2 12..4(11)..3
9 48 105 137631 2199f 3 14..2(22)..5
10 36 77 38231 9557 2 12..5(11)..3
11 98 203 602935 93337 3 121..3(22)..13
12 50 109 152919 25557 2 12..6(11)..3
13 160 305 2202015 21999f 3 14..3(22)..5
14 100 205 611671 95557 2 12..7(11)..3
15 295 504 9646903 933337 3 121..4(22)..13
16 172 317 2446679 255557 2 12..8(11)..3
17 357 878 35232159 219999f 3 14..4(22)..5
18 298 509 9786711 955557 2 12..9(11)..3
19 683 1332 154350391 9333337 3 121..5(22)..13
20 372 893 39146839 2555557 2 12..10(11)..3
21 1144 2049 563714463 2199999f 3 14..5(22)..5
22 692 1341 156587351 9555557 2 12..11(11)..3
23 1963 3636 2469606199 93333337 3 121..6(22)..13
24 1172 2109 626349399 25555557 2 12..11(11)..3
25 2437 4174 9019431327 21999999f 3 14..6(22)..5
26 1972 3645 2505397591 95555557 2 12..13(11)..3
27 4555 7348 39513699127 933333337 3 121..7(22)..13
28 2580 4413 10021590359 255555557 2 12..13(11)..3
29 7672 - 144310901151 219999999f 3 14..7(22)..5
30 4628 7485 40086361431 955555557 2 12..15(11)..3
31 - - (632219185975 9333333337 3) 121..8(22)..13
32 7860 - 160345445719 2555555557 2 12..16(11)..3
...
We observe that the following hexadecimal pattern seems to hold, indicating an underlying algebraic generator. To produce a term in A334771, we cycle through the hexadecimal {“21_f”, “9_7”, “93_7”, “25_7”}, inserting at the underscore ⌊k/4⌋ copies of the following for k (mod 4): for even residue: “5”, for residue 1: “9”, and for residue 3: “3”. Therefore we would expect the following terms to occur after A334771(32) = 160345445719: 2308974418335, 641381782871, 10115506975543, 2565527131479.
In looking at the problem of these XOR triangles, we might be led to conclude, as Stephen Wolfram had regarding cellular automaton rule 30, that it is “extremely hard to rigorously prove things about [them]”[4], and at any rate the author may not be as ably equipped to do so as others might prove. This said, we might look to construction to determine something about this sequence.
In examining the infix modules (see Section 6), we note recipe (11) is the only available recipe for frame width j = 2, and (22) the only recipe for j = 3. We also observe that prefix-suffix 12..3 is the sole facilitator for (11), with a total run length of 6 (even), and an odd number of run lengths that, coupled with any number of copies of (11), guarantees the necessary odd total number of run lengths in to furnish an RST. Minimizing frame width j also minimizes binary integer length ℓ. Therefore, for even k, the smallest seed n is of the pattern 12..k/2 × (11)..3, i.e., in the linear recurrence (5, −4) beginning with {151, 599}. Corollary to this is the fact that RSTs with odd binary integer length ℓ have frame width j > 2.
Thus the frame width j = 3 for odd k. For frame width j = 3, the only infix module is recipe (22), with total bit length of 4. There are three lower binary weight prefix-suffix combinations 14..5, 11112..32, 113..2112, 1212..213. Of these the lightest are 14..5 with total bit length 10, and 1212..213 with total bit length 12. The first prefix-suffix combination, when containing any number of modules (22) (including none), furnishes the smallest solutions of seed n for j ≡ 1 (mod 4), but cannot furnish seed n for j ≡ 3 (mod 4). The recipe 1212..213 is the smallest solution for seed n for j ≡ 3 (mod 4). Therefore, the smallest solutions for seed n and j ≡ 1 (mod 4) are in linear recurrence (17, −16) {543, 8607}, and for j ≡ 4 (mod 4) are in linear recurrence (17, −16) {2359, 37687}. There are no other available solutions for these frame widths, and we might extend the sequence indefinitely.
Therefore we see that A334771 is a linear recurrence with kernel {0, 0, 0, 17, 0, 0, 0, −16}, beginning with {543, 151, 2359, 599, 8607, 2391, 37687, 9559}. (See Code 5.4)
Figure 5.2 shows the smallest instances n of RSTs that generate CZTs with side length k = 1..16, from left to right, top to bottom. The italics designate the index of n in A334769, while the bold represents n itself. (see an expanded table featuring k = 1..64 ):
The following abbreviated table summarizes facts about rotationally symmetrical XOR-triangles with central zero-triangles. The first column (i) is the index in A334769 (the sequence of RSTs with central-zero triangles), while RST refers to the index in A334556 (the sequence of RSTs). The number n, expanded in base 2 as b(n), generates the XOR-triangle T(n) with the properties of frame width j and side length k, and with the number of zero-triangles shown at right with side-lengths according to the number of their position in the list. Asterisks denote the first occurence of the value in the corresponding sequence. (Click for a full list of 10000 RSTs that have CZTs):
i RST n j k A333624 row n
1 10 151 *2 *2 3, 4
2 11 233 2 2 3, 4
3 12 543 *3 *1 1, 0, 0, 3
4 13 599 2 *4 6, 3, 0, 1
5 18 937 2 4 6, 3, 0, 1
6 19 993 3 1 1, 0, 0, 3
7 20 1379 3 2 9, 1, 3
8 21 1483 3 2 6, 7
9 22 1589 3 2 9, 1, 3
10 23 1693 3 2 6, 7
11 24 2359 3 *3 9, 6, 1
12 25 2391 2 *6 9, 3, 0, 0, 0, 1
13 30 3753 2 6 9, 3, 0, 0, 0, 1
14 31 3785 3 3 9, 6, 1
15 48 8607 3 *5 3, 3, 0, 3, 1
16 49 9559 2 *8 12, 3, 0, 0, 0, 0, 0, 1
...
Example: the third rotationally symmetrical XOR-triangle (RST) that has a central zero-triangle (CZT) is T(543), which is also the 12th term in the sequence of all RSTs. T(543) has a CZT of side length k = 1 and frame width j = 3. T(543) has 1 zero-triangle of side length 1 (i.e., the CZT), and 3 of side length 4. Further, T(543) is generated by the smallest n with frame length j = 3 and also CZT edge length k = 1.
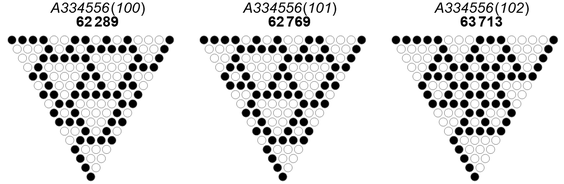
We cannot use A333624 as a "signature" for a given RST. Firstly, the number n and its binary integer reversal n′ = A030101(n) have the same number of zero-triangles of a given side length k as a consequence of translational symmetry. Further, the same quantity of ZTs of the same side length k may arise outside of translational symmetry, e.g., terms 100, 101, and 102 of A334556, i.e., n = {62289, 62769, 63713} shown in Figure 5.3. These have 10 ZTs with k = 1, and 3 each of ZTs with 2 ≤ k ≤ 4, thus share the same terms in A333624, i.e., {10, 3, 3, 3}:
Numbers n that produce RSTs with zero-triangles with recordsetting side length k.
The numbers that set records for ZTs with the largest side length k appear below and in OEIS A335077. In the table, i is the index of the record, CZT is the index of n in A334769, RST the index of n in A334556, n along with its hexadecimal expansion that brings out the pattern of bits in n, and GZT is the greatest zero triangle side length, k = A334770(CZT), j = A334796(CZT):
i CZT RST n n_16 GZT k j Run Length Recipe
------------------------------------------------------------------------------
1 0 1 1 1 0 0 0 1
2 0 2 11 b 1 0 0 112
3 0 4 39 27 2 0 0 123
4 3 12 543 21f 4 1 3 145
5 12 25 2391 957 6 6 2 121111113
6 16 49 9559 2557 8 8 2 12.. 4(11)..3
7 36 77 38231 9557 10 10 2 12.. 5(11)..3
8 50 109 152919 25557 12 12 2 12.. 6(11)..3
9 100 205 611671 95557 14 14 2 12.. 7(11)..3
10 172 317 2446679 255557 16 16 2 12.. 8(11)..3
11 298 509 9786711 955557 18 18 2 12.. 9(11)..3
12 372 893 39146839 2555557 20 20 2 12..10(11)..3
13 692 1341 156587351 9555557 22 22 2 12..11(11)..3
14 1172 2109 626349399 25555557 24 24 2 12..12(11)..3
15 1972 3645 2505397591 95555557 26 26 2 12..13(11)..3
16 2580 4413 10021590359 255555557 28 28 2 12..14(11)..3
17 4628 7485 40086361431 955555557 30 30 2 12..15(11)..3
...
This sequence contains n that produce T(m) with a recordsetting side length K of its largest zero-triangle. For 1 < i < 3, T(A355077(i)) only has eccentric zero triangles. T(A355077(4)) has a singleton zero at center, thus a central zero triangle (CZT) of k = 1. For i > 4, all T(A335077(i)) have CZTs.
The number 543 = A281482(4); we observe that A281482(2x) produces RSTs, and only for 0 ≤ i ≤ 2 do we have eccentric zero triangles larger than any possible CZT. For A281482(2³) = 131583, the side length of its eccentric zero triangles prove much smaller than the largest possible CZT.
Since this sequence wants to maximize the side length K of the largest triangle, we see that the largest triangle possible is the CZT. We note frame width j ≥ 2, since j = 1 requires a run of (k + 1) ones delimited by at least 1 zero; such a width implies that these zeros occur at the beginning and end of b(n). However, beginning binary notation with a leading zero is not permitted. Therefore, if it is possible, we will only see T(n) with j > 1.
The numbers that produce recordsetting n are the smaller of the binary reverse of n, therefore binary weight favors the least significant digits. Thus we see a 1 followed by a number of zeros in a "prefix" A that, along with a suffix C, must have the same number of bits. For RSTs with a CZT, we have only one way to produce a solid run of (k + 1) zeros, that is, by dithering bits, which necessitates paired 0 and 1, therefore, we have even k for i > 4.
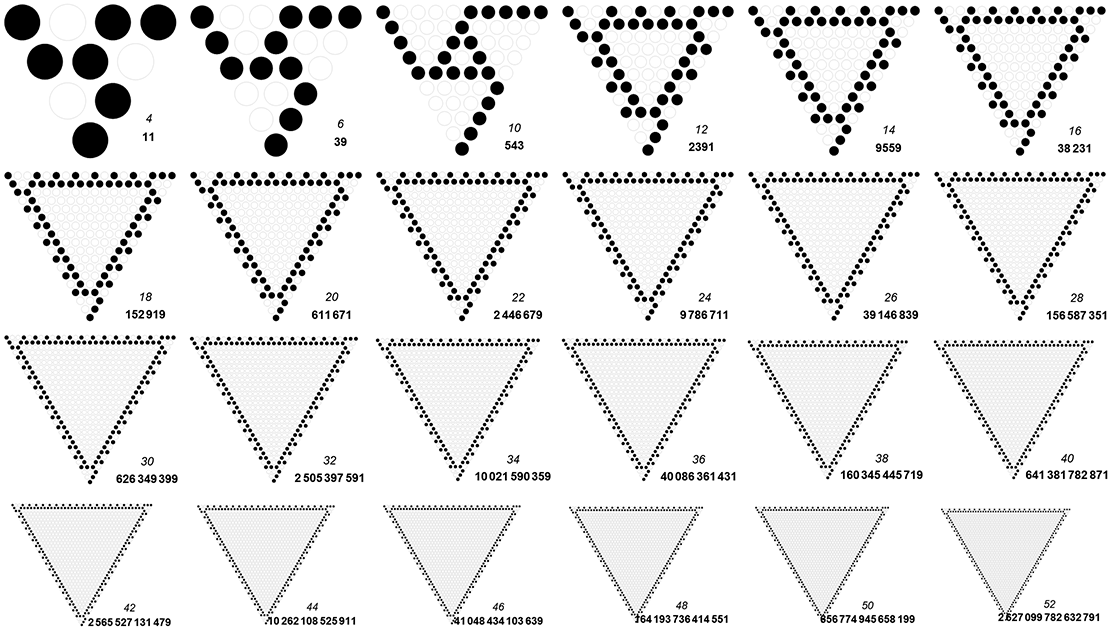
A run-length formula for A335077(i) with i > 4 is 12..x(11)..3, meaning that we have 1 one, 2 zeros, any number x of paired 1-0 bits, and a run of 3 ones. Aside from the reversal of this pattern, which puts a greater binary weight in the most significant 3 bits, there is no other way to construct a smaller (or any) CZT with frame size j = 2. The smallest terms of such a sequence are the even terms of A334771, i.e., {(39), 151, 599, 2391, 9559, …}, with parenthetic 39 such as it is the zero-case of the pattern, i.e., run length recipe 123 without the dither frame. This equates to linear recurrence kernel (5, -4) starting with {39, 151}. We see that the CZTs produced for the first terms prove smaller than those produced by A281482(2x), but given the geometric sparsity of terms in that sequence, we find that there are no smaller n that generate a larger zero triangle in an RST than for the terms in the linear recurrence..
Therefore the sequence includes {1, 11, 39, 543}, then terms in the linear recurrence (5, −4) starting from {2391, 9559}.
Figure 5.6 diagrams these (excepting the first term), along with RSTs generated by the linear recurrence:
6. Definitions for n that produce RSTs with CZTs.
We note certain patterns among the figures T(n) for n in A334771. Figure 6.1:

Examination of the seed bitstrings b(n) that produce RSTs with a CZT.
Let A be the “prefix”, C the “infix”, and B the “suffix” of a pattern of ℓ bits in the binary representation b(n) for n in A334771. The infix may be composed of modules, especially for j = 2 or 3. Let w denote the bit-length of the infix module m. We note the following as regards rotationally symmetrical XOR-triangles:
1.) Prefixes A begin and suffixes B end with a 1-bit.
2.) Bit-lengths of A and B are identical.
3.) A central zero-triangle of side length k necessitates w | k, therefore the number of infix modules is k/w. If the infix does not appear to have modules, it may possess some degree of transformational symmetry. There is no necessity to maintain modularity with chirality preserved or with multiple modules: any pattern in b(n) that can give rise to a run of (k + 1) ones at iteration (j − 1) can be found.
The prefix must have binary weight less than that of the suffix, generally, the binary weight (i.e., the presence of 1-bits) favors the least significant places for the first instances of a given value of j or k.
For a frame with width j = 2, at least one method of producing the 2-frame involves a prefix A = 100…, suffix B = …111, with infix module …10…. Assembling parts AB → n = 39, AMB → n = 151, AMMB → n = 599, etc. This implies a linear recurrence (5, –4) starting from 39 and 151: {39, 151, 599, 2391, 9559, 38231, …}, i.e., coefficients of (39 – 44x)/(1 – 5x + 4x²). The binary reverse of these numbers belong to the same recurrence instead starting with (57, 233): {57, 233, 937, 3753, 15017, 60073, …}, g.f., (57 – 52x)/(1 – 5x + 4x²). The first term of these recurrences do not have a CZT, but all others do. For j = 3, there are at least two sources of j = 3.
Since the XOR function that generates the XOR-triangle “tapers” such that the resulting output decrements in binary integer length, we find that the infix must have binary integer length (j + k). However, some of the input that produces the solid run of 1s may derive from a portion of the prefix and suffix. Therefore it might not be necessary that the infix length is divisible into modules.
Run Length Recipes of b(n).
We might construct n using a “recipe” of run lengths, so long as they are odd in number. We construe the first run length to pertain to 1, then alternate between 0 and 1 as we proceed, so that odd-indexed run lengths pertain to 1 and even-indexed to 0 (cf. OEIS A101211, A318927). This way we can concoct a bitstring seed b(n) and produce T(n). The run length recipe method R(n) is usually more succinct than b(n). For example, we might express b(40679) = 10011110111001112 instead as R(40679) = {1,2,4,1,3,2,3}.
Using R(n), we may determine the prefix, infix module, and suffix of a given seed n that produces an RST with a CZT. For instance, we find that coefficients n of the series (39 - 44x)/(1 - 5x + 4x²) and their binary-integer-reversals generate RSTs with a CZT (terms in A334769) such that frame width j = 2. We might instead write a run length recipe “12..11..3”, prefix, infix module, and suffix, reversal of all as “3..11..21” also producing terms in A334769. The terms {39, 151, 599, 2391, 9559, 38231, …} become {“123”, “321”, “12113”, “31121”, “1211113”, “3111121”, …}.
Through observation we have the following linear recurrences that generate some solutions with a given value of j:
j LR Lower Upper
-----------------------------------------------------
2 (5, –4) {39, 151} {57, 223}
3 (17, –16) {543, 8607} {993, 15969}
{1379, 22115} {1589, 25397}
{1483, 23755} {1693, 27037}
{2359, 37687} {3785, 60617}
4 (17, –16) {25525, 408501} {22243, 356067}
{39047, 624775} {57625, 921881}
{40679, 650983} {59257, 948089}
{171475, 2743763} {208613, 3337957}
{356067, 5697251} {408501, 6536117}
Figure 6.2 shows XOR-triangles for the smallest 6 terms of the above linear recurrences, the “lower” relation at left, the “upper” at right, plotted in book-matched fashion. The last row is the smallest relation that pertains to j = 5. Written in hexadecimal, the numbers in the last row are {574b4a3, 574b4b4a3, 574b4b4b4a3, …} and their integer reversals. (See a full table that examines the hexadecimal patterns in A334796.)

In an attempt to further ascertain metrics and reasons for the production of the triangles, we repeat the table with the lower and upper first terms in hexadecimal, but also examine run lengths:
j LR Lower Upper Recipe of Lower (reverse for Upper)
-------------------------------------------------------------------------------------------
2 (5, –4) {27, 97} {39, df} 12..(11)..3
3 (17, –16) {21f, 219f} {3e1, 3e61} 14..(22)..5
{563, 5663} {635, 6335} 11112..(22)..32
{5cb, 5ccb} {69d, 699d} 113..(22)..2112
{937, 9337} {ec9, ecc9} 1212..(22)..213
4 (17, –16) {63b5, 63bb5} {56e3, 56ee3} 233..(13)..121111
{9887, 98887} {e119, e1119} 1223..(13)..143
{9ee7, 9eee7} {e779, e7779} 1241..(31)..323
{29dd3, 29ddd3} {32ee5, 32eee5} 111231..(31)..31122
{56ee3, 56eee3} {63bb5, 63bbb5} 11112131..(31)..332
There appear to be more generators for j = 5. Among the sequence of the smallest n that produces a given CZT with a given value of j, only the first three seem to appear for j ≤ 28. It appears that module bit-length w is 2 for j = 2, 4 for both j = 2 and 3, and 8 for both j = 5 and 6 (more investigation is needed). Because of this, it seems useful to express n in hexadecimal to examine the patterns in the frames. (This shall be a subject for an exhaustive study forthcoming.)
We can write a program that roots through all the RSTs that produce CZTs (i.e., all n in A334769) to determine the recipe for a family of n. The program is not perfect, but reproduces the recipes observed in the tables above.
j Least n Recipe
--------------------------
2 39 12..(11)..3
3 543 14..(22)..5
1379 11112..(22)..32
1483 113..(22)..2112
2359 1212..(22)..213
4 22243 111121..(31)..332
39047 1223..(13)..143
40679 1241..(31)..323
171475 111231..(31)..31122
356067 11112131..(31)..332
5 33151 16..(112112)..117
34591 143..(44)..35
35535 131111..(112112)..224
36015 1322..(112112)..11114
131583 18..(44)..9
150839 121221..(121121)..12213
165299 1114..(112112)..1121222
182651 1122121..(211211)..11412
357539 1111311..(211211)..211132
359459 11115..(44)..4132
382603 1131112..(112112)..113112
384523 11314..(44)..5112
599479 1212121..(121121)..121213
607191 121114.(44).41113
630279 1222..(44)..463
653415 126..(44)..4223
1121807 1313..(44)..454
1175791 135..(44)..4314
1268295 1221112..(112112)..112133
1291431 123121..(121121)..1211123
1337715 1113211..(211211)..211322
1345427 111214..(44)..42122
1453371 1123112..(112112)..112312
1491931 112124..(44)..41212
2197407 1424..(44)..425
2444119 12111112..(112112)..112111113
2737107 111234..(44)..41122
2952987 112114..(44)..43212
4271423 151211..(211211)..21126
4302271 15211..(211211)..211216
4919063 121124..(44)..43113
4949911 121134..(44)..42113
8851231 1434..(44)..435
46754171 112212..(112112)..11412
8621515263 1844..(44)..449
The list of recipes is not guaranteed to have exhausted the possibilities, though it seems that there is a limit as to which infix modules would maintain a sustained run of 1s at iteration m = (j − 1). For j = 2, only (11) is possible, and only (22) seems to sustain j = 3. Counting reversals only once, j = 4 seems to be produced by (13), but j = 5 is produced by both (44) and (112112).
j Recipe Binary
----------------------------------
2 (11) 10
3 (22) 1100
4 (13) 1000 / 1110
5 (44) 11110000
(112112) 10110100
6 (1115) 10100000 / 11111010
(1232) 10011100 / 11000110
7 (1133) etc.
(1214)
(111122)
(26)
8 (111113)
(111212)
(1124)
(1223)
(17)
(35)
We note that the sum of these run lengths, S ≥ n.
Figure 6.3 demonstrates the above-mentioned infix modules without prefix and suffix:
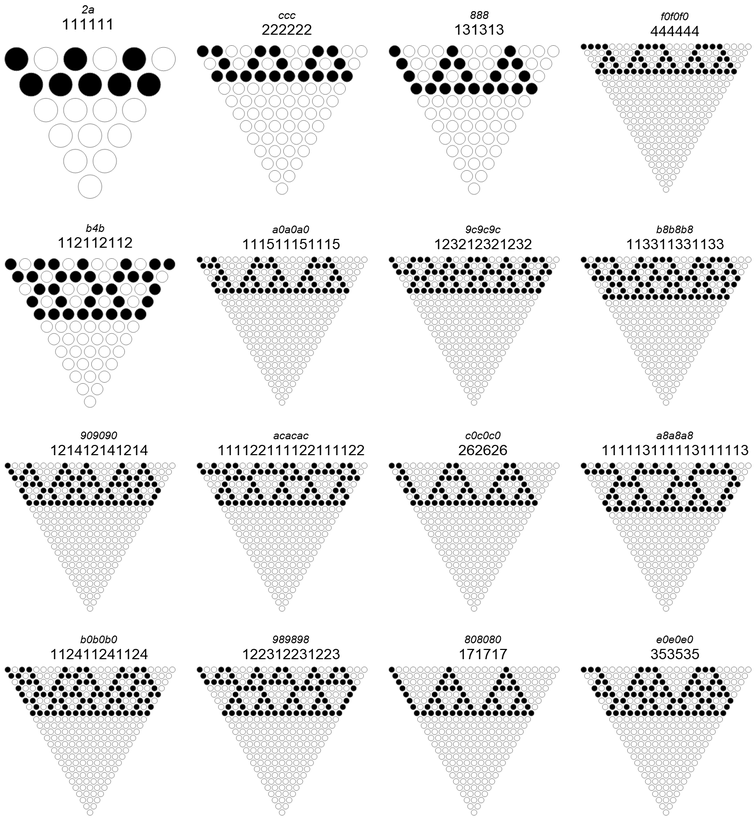
Let’s take a look at the structure of a recipe for j = 5, (112112):
1 . 1 1 . 1 . . 1 . 1 1 . 1 . . ⇒ (112112)
1 1 . 1 1 1 . 1 1 1 . 1 1 1 . ⇒ (31)
. 1 1 . . 1 1 . . 1 1 . . 1 ⇒ (22)
1 . 1 . 1 . 1 . 1 . 1 . 1 ⇒ (11)
1 1 1 1 1 1 1 1 1 1 1 1 ⇒ _
We note that at each iteration m (starting from m = 0 at top) we have a recipe progression (112112) → (31) → (22) → (11) → _ that sustains j − m.
Examining the other infix module (44) pertaining to j = 5:
1 1 1 1 . . . . 1 1 1 1 . . . . ⇒ (44)
. . . 1 . . . 1 . . . 1 . . . ⇒ (13)
. . 1 1 . . 1 1 . . 1 1 . . ⇒ (22)
. 1 . 1 . 1 . 1 . 1 . 1 . ⇒ (11)
1 1 1 1 1 1 1 1 1 1 1 1 ⇒ _
This is an alternate progression (44) → (13) → (22) → (11) → _ for j = 5.
We find that we might ascertain that the recipes for 2 < j < 5 are complete, and that with further study, we might complete the possible solutions for other values.
7. A tree of infix module recipe progressions.
We note that the recipe (13) is transitive: it applies to either parity, while (112112) reverses parity as the submodule has an odd number of run lengths. This may lead us to conflate (13) and (31). When we write recipes for full triangles, it is acceptable to conflate the reversals, since parity is preserved in the order of appearance of the infix module. When considered outside of a triangle, we see that parity is indeed important. Therefore we write the run length that pertains to 1 first by convention here
The two most-recent diagrams give us the idea that we might work “up” (or reverse-iterate) from a solid bar of 1s and generate all possible arrangements of bits in previous iterations.
There is uncertainty in reversal of the XOR function. We know that the XOR function outputs 0 given agreement: this means, working from a single 0 backward, we either have two 1s or two 0s. The other possible output of the XOR function results in disagreement, therefore we either have input {0, 1} or {1, 0}. Therefore, in reversing the function we are presented with alternatives.
Let us set the solid bar of 1s at j = 1. Further, let us count term terms i in row j, thus we have T(i, j). Reverse iteration of the XOR function might be regarded as using the terms T(i − 1, j− 1) as maintenance or reversal of parity of T(i − 1, j) to furnish T(i, j). In other words, if T(i − 1, j − 1) = 0, T(i − 1, j) = T(i, j), else T(i − 1, j) + 1 (mod 2) = T(i, j). Simply,
T(i, j) = T(i − 1, j) + T(i − 1, j − 1) (mod 2).
and we might begin using 1 or 0 to begin row j. Looking at row (j − 1), we take 0 to connote maintenance of parity and 1 as change of parity. Thus, when we have an odd-indexed run (pertaining to 1s) we have alternation of parity (dithering), and when we have an even-indexed run, we have maintenance of parity in the present row.
Thus we have dither (11) at j = 2. From this, we know that there are two alternatives, dither starting with 1, and dither starting with 0, which are both the same dither, and there can only be dither above a solid bar of 1s.
. 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 → _
For j = 3, we have a 2-dither, that is, the alternation of run length 2 of zeros, and run length 2 of ones, i.e., (22). Again, this could start with a 0 or a 1, but constitute merely horizontal translations of the same pattern.
. . 1 1 . . 1 1 . . 1 1 . . → (22)
. 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 → _
There arise 2 and only 2 ways to construct j = 4, one that produces (13), writing the run length that generates a run of 1s first:
. . . 1 . . . 1 . . . 1 . . . → (13)
. . 1 1 . . 1 1 . . 1 1 . . → (22)
. 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 → _
the other produces (31), writing that run length first which produces a run of ones, thus (31) = 11102:
1 1 1 . 1 1 1 . 1 1 1 . 1 1 1 → (31)
. . 1 1 . . 1 1 . . 1 1 . . → (22)
. 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 → _
The two methods of producing j = 4 give rise each to the following: (13) → (44) pertaining to j = 5, and is transitive:
1 1 1 1 . . . . 1 1 1 1 . . . . → (44)
. . . 1 . . . 1 . . . 1 . . . → (13)
. . 1 1 . . 1 1 . . 1 1 . . → (22)
. 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 → _
We see (31) gives rise to internally transitive (112112):
1 . 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
. 1 1 . . 1 1 . . 1 1 . . 1 → (22)
1 . 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 1 → _
Therefore there are only 2 methods for j = 5.
Frame width j = 6 has the following:
. 1 . 1 1 1 1 1 . 1 . 1 1 1 1 1 → (5111)
1 1 1 . . . . 1 1 1 1 . . . . → (44)
. . 1 . . . 1 . . . 1 . . . → (13)
. 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
1 . 1 . . . . . 1 . 1 . . . . . → (1115)
1 1 1 . . . . 1 1 1 1 . . . . → (44)
. . 1 . . . 1 . . . 1 . . . → (13)
. 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
. . 1 . . 1 1 1 . . 1 . . 1 1 1 → (1232)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
1 1 . 1 1 . . . 1 1 . 1 1 . . . → (2321)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
Thus 4 distinct patterns for j = 6: (1115), (5111), (1232), (2321).
For j = 7 we have 8 distinct patterns:
1 . 1 1 . . 1 . 1 . 1 1 . . 1 . 1 . 1 → (111122)
1 1 . 1 . 1 1 1 1 1 . 1 . 1 1 1 1 1 → (5111)
. 1 1 1 1 . . . . 1 1 1 1 . . . . → (44)
1 . . . 1 . . . 1 . . . 1 . . . → (13)
1 . . 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 1 → _
. 1 . . 1 1 . 1 . 1 . . 1 1 . 1 . 1 . → (221111)
1 1 . 1 . 1 1 1 1 1 . 1 . 1 1 1 1 1 → (5111)
. 1 1 1 1 . . . . 1 1 1 1 . . . . → (44)
1 . . . 1 . . . 1 . . . 1 . . . → (13)
1 . . 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 1 → _
1 . . 1 1 1 1 1 1 . . 1 1 1 1 1 1 → (62)
1 . 1 . . . . . 1 . 1 . . . . . → (1115)
1 1 1 . . . . 1 1 1 1 . . . . → (44)
. . 1 . . . 1 . . . 1 . . . → (13)
. 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
. 1 1 . . . . . . 1 1 . . . . . . → (26)
1 . 1 . . . . . 1 . 1 . . . . . → (1115)
1 1 1 . . . . 1 1 1 1 . . . . → (44)
. . 1 . . . 1 . . . 1 . . . → (13)
. 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
1 1 1 . . . 1 . 1 1 1 . . . 1 . 1 → (1133)
. . 1 . . 1 1 1 . . 1 . . 1 1 1 → (1232)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
. . . 1 1 1 . 1 . . . 1 1 1 . 1 . → (3311)
. . 1 . . 1 1 1 . . 1 . . 1 1 1 → (1232)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
. 1 . . 1 . . . . 1 . . 1 . . . . → (1214)
1 1 . 1 1 . . . 1 1 . 1 1 . . . → (2321)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
1 . 1 1 . 1 1 1 1 . 1 1 . 1 1 1 1 → (4121)
1 1 . 1 1 . . . 1 1 . 1 1 . . . → (2321)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
For j = 8, we have:
1 . . 1 . . . 1 1 . . 1 . . . 1 1 . . 1 → (1223)
1 . 1 1 . . 1 . 1 . 1 1 . . 1 . 1 . 1 → (111122)
1 1 . 1 . 1 1 1 1 1 . 1 . 1 1 1 1 1 → (5111)
. 1 1 1 1 . . . . 1 1 1 1 . . . . → (44)
1 . . . 1 . . . 1 . . . 1 . . . → (13)
1 . . 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 1 → _
. 1 1 . 1 1 1 . . 1 1 . 1 1 1 . . 1 1 . → (3221)
1 . 1 1 . . 1 . 1 . 1 1 . . 1 . 1 . 1 → (111122)
1 1 . 1 . 1 1 1 1 1 . 1 . 1 1 1 1 1 → (5111)
. 1 1 1 1 . . . . 1 1 1 1 . . . . → (44)
1 . . . 1 . . . 1 . . . 1 . . . → (13)
1 . . 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 1 → _
1 1 . . . 1 . . 1 1 . . . 1 . . 1 1 . . → (1223)
. 1 . . 1 1 . 1 . 1 . . 1 1 . 1 . 1 . → (221111)
1 1 . 1 . 1 1 1 1 1 . 1 . 1 1 1 1 1 → (5111)
. 1 1 1 1 . . . . 1 1 1 1 . . . . → (44)
1 . . . 1 . . . 1 . . . 1 . . . → (13)
1 . . 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 1 → _
. . 1 1 1 . 1 1 . . 1 1 1 . 1 1 . . 1 1 → (3211)
. 1 . . 1 1 . 1 . 1 . . 1 1 . 1 . 1 . → (221111)
1 1 . 1 . 1 1 1 1 1 . 1 . 1 1 1 1 1 → (5111)
. 1 1 1 1 . . . . 1 1 1 1 . . . . → (44)
1 . . . 1 . . . 1 . . . 1 . . . → (13)
1 . . 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 1 1 → _
1 . . . 1 . 1 . 1 . . . 1 . 1 . 1 . → (111113)
1 . . 1 1 1 1 1 1 . . 1 1 1 1 1 1 → (62)
1 . 1 . . . . . 1 . 1 . . . . . → (1115)
1 1 1 . . . . 1 1 1 1 . . . . → (44)
. . 1 . . . 1 . . . 1 . . . → (13)
. 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
. 1 1 1 . 1 . 1 . 1 1 1 . 1 . 1 . 1 → (311111)
1 . . 1 1 1 1 1 1 . . 1 1 1 1 1 1 → (62)
1 . 1 . . . . . 1 . 1 . . . . . → (1115)
1 1 1 . . . . 1 1 1 1 . . . . → (44)
. . 1 . . . 1 . . . 1 . . . → (13)
. 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
1 1 . 1 1 1 1 1 1 1 . 1 1 1 1 1 1 1 → (71)
. 1 1 . . . . . . 1 1 . . . . . . → (26)
1 . 1 . . . . . 1 . 1 . . . . . → (1115)
1 1 1 . . . . 1 1 1 1 . . . . → (44)
. . 1 . . . 1 . . . 1 . . . → (13)
. 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
. . 1 . . . . . . . 1 . . . . . . . → (17)
. 1 1 . . . . . . 1 1 . . . . . . → (26)
1 . 1 . . . . . 1 . 1 . . . . . → (1115)
1 1 1 . . . . 1 1 1 1 . . . . → (44)
. . 1 . . . 1 . . . 1 . . . → (13)
. 1 1 . . 1 1 . . 1 1 . . → (22)
1 . 1 . 1 . 1 . 1 . 1 . → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
1 . 1 . . . . 1 1 . 1 . . . . 1 1 . → (1124)
1 1 1 . . . 1 . 1 1 1 . . . 1 . 1 → (1133)
. . 1 . . 1 1 1 . . 1 . . 1 1 1 → (1232)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
. 1 . 1 1 1 1 . . 1 . 1 1 1 1 . . 1 → (4211)
1 1 1 . . . 1 . 1 1 1 . . . 1 . 1 → (1133)
. . 1 . . 1 1 1 . . 1 . . 1 1 1 → (1232)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
1 1 1 1 . 1 . . 1 1 1 1 . 1 . . 1 1 → (4211)
. . . 1 1 1 . 1 . . . 1 1 1 . 1 . → (3311)
. . 1 . . 1 1 1 . . 1 . . 1 1 1 → (1232)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
. . . . 1 . 1 1 . . . . 1 . 1 1 . . → (1124)
. . . 1 1 1 . 1 . . . 1 1 1 . 1 . → (3311)
. . 1 . . 1 1 1 . . 1 . . 1 1 1 → (1232)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
1 1 . . . 1 1 1 1 1 . . . 1 1 1 1 1 → (53)
. 1 . . 1 . . . . 1 . . 1 . . . . → (1214)
1 1 . 1 1 . . . 1 1 . 1 1 . . . → (2321)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
. . 1 1 1 . . . . . 1 1 1 . . . . . → (35)
. 1 . . 1 . . . . 1 . . 1 . . . . → (1214)
1 1 . 1 1 . . . 1 1 . 1 1 . . . → (2321)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
1 . . 1 . . 1 . 1 . . 1 . . 1 . 1 . → (111212)
1 . 1 1 . 1 1 1 1 . 1 1 . 1 1 1 1 → (4121)
1 1 . 1 1 . . . 1 1 . 1 1 . . . → (2321)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
. 1 1 . 1 1 . 1 . 1 1 . 1 1 . 1 . 1 → (212111)
1 . 1 1 . 1 1 1 1 . 1 1 . 1 1 1 1 → (4121)
1 1 . 1 1 . . . 1 1 . 1 1 . . . → (2321)
. 1 1 . 1 . . 1 . 1 1 . 1 . . → (112112)
1 . 1 1 1 . 1 1 1 . 1 1 1 . → (31)
1 1 . . 1 1 . . 1 1 . . 1 → (22)
. 1 . 1 . 1 . 1 . 1 . 1 → (11)
1 1 1 1 1 1 1 1 1 1 1 → _
Now that we have rigorously constructed all possible chains 2 < j < 10, (originating from j = 1) we can summarize them:
(0)→(11)→(22)→(13)→(44)→(5111)→(111122)→(1223)→(134134)→(11211145)
(0)→(11)→(22)→(13)→(44)→(5111)→(111122)→(1223)→(134134)→(54111211)
(0)→(11)→(22)→(13)→(44)→(5111)→(111122)→(3221)→(1121311213)→(11212432)
(0)→(11)→(22)→(13)→(44)→(5111)→(111122)→(3221)→(1121311213)→(23421211)
(0)→(11)→(22)→(13)→(44)→(5111)→(221111)→(1223)→(134134)→(11211145)
(0)→(11)→(22)→(13)→(44)→(5111)→(221111)→(1223)→(134134)→(54111211)
(0)→(11)→(22)→(13)→(44)→(5111)→(221111)→(3221)→(1121311213)→(11212432)
(0)→(11)→(22)→(13)→(44)→(5111)→(221111)→(3221)→(1121311213)→(23421211)
(0)→(11)→(22)→(13)→(44)→(1115)→(62)→(111113)→(224224)→(11131513)
(0)→(11)→(22)→(13)→(44)→(1115)→(62)→(111113)→(224224)→(31513111)
(0)→(11)→(22)→(13)→(44)→(1115)→(62)→(311111)→(1122211222)→(12313213)
(0)→(11)→(22)→(13)→(44)→(1115)→(62)→(311111)→(1122211222)→(31231321)
(0)→(11)→(22)→(13)→(44)→(1115)→(26)→(71)→(11111121111112)→(12223222)
(0)→(11)→(22)→(13)→(44)→(1115)→(26)→(71)→(11111121111112)→(22232221)
(0)→(11)→(22)→(13)→(44)→(1115)→(26)→(17)→(88)→(11111119)
(0)→(11)→(22)→(13)→(44)→(1115)→(26)→(17)→(88)→(91111111)
(0)→(11)→(22)→(31)→(112112)→(1232)→(1133)→(1124)→(125125)→(11112163)
(0)→(11)→(22)→(31)→(112112)→(1232)→(1133)→(1124)→(125125)→(36121111)
(0)→(11)→(22)→(31)→(112112)→(1232)→(1133)→(4211)→(1112311123)→(11221423)
(0)→(11)→(22)→(31)→(112112)→(1232)→(1133)→(4211)→(1112311123)→(32412211)
(0)→(11)→(22)→(31)→(112112)→(1232)→(3311)→(4211)→(1112311123)→(11221423)
(0)→(11)→(22)→(31)→(112112)→(1232)→(3311)→(4211)→(1112311123)→(32412211)
(0)→(11)→(22)→(31)→(112112)→(1232)→(3311)→(1124)→(125125)→(11112163)
(0)→(11)→(22)→(31)→(112112)→(1232)→(3311)→(1124)→(125125)→(36121111)
(0)→(11)→(22)→(31)→(112112)→(2321)→(1214)→(53)→(1111411114)→(11122522)
(0)→(11)→(22)→(31)→(112112)→(2321)→(1214)→(53)→(1111411114)→(22522111)
(0)→(11)→(22)→(31)→(112112)→(2321)→(1214)→(35)→(116116)→(11111272)
(0)→(11)→(22)→(31)→(112112)→(2321)→(1214)→(35)→(116116)→(27211111)
(0)→(11)→(22)→(31)→(112112)→(2321)→(4121)→(111212)→(233233)→(11311414)
(0)→(11)→(22)→(31)→(112112)→(2321)→(4121)→(111212)→(233233)→(41411311)
(0)→(11)→(22)→(31)→(112112)→(2321)→(4121)→(212111)→(1212212122)→(12121333)
(0)→(11)→(22)→(31)→(112112)→(2321)→(4121)→(212111)→(1212212122)→(33312121)
Figure 6.4 shows the resultant tree where level j = 1 at left and j = 10 at right, with {1, 1, 1, 2, 2, 4, 8, 12, 12, 24, …} nodes in each level.
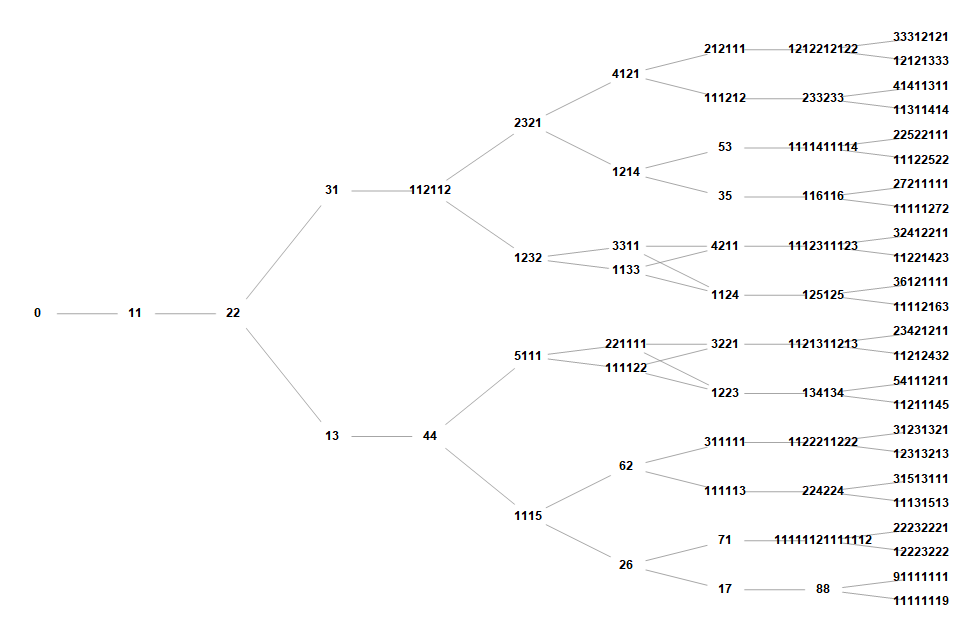
Therefore we may classify RSTs with CZTs in terms of their lineage in the tree. There seems to be many prefix-suffix combinations that might be considered copacetic with certain infix modules such that there are null infixes at the head of all the families.
8. Grain Size of ZTs in RSTs.
Let’s define “grain size” as an aggregate side length k for all zero-triangles in an RST, in other words, all zero-triangles, including the CZT, are of side length k. Because the matrix of k-ZTs may encounter the edge of the triangle, we accept the artifacts of clipping that results in a ZT with a smaller edge length at the edge of the XOR-triangle. In the case of k = 1, we can produce a "pure" grain size of 1, a matrix or field of 1-ZTs. For larger k, we cannot avoid clipping ZTs at the edge of the XOR-triangle, yet we end up with a rotationally symmetrical XOR-triangle.
Figure 8.1 shows examples of grain size 1, 2, and 3 from left to right. The rightmost triangle represents the “best we can do” regarding grain size 3 for RSTs with CZTs, since a CZT of k = 3 placed at center necessitates a 0 at the first and last bits of the seed n (which is not permitted):
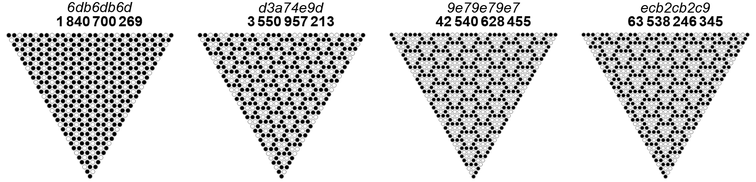
We might regard the exercise as an attempt to fit zero-triangles of size k with a blunted (hexagonal) border 1 bit thick of 1s that are permitted to “meld” so that we never have a thicker border and such that we admit no other ZTs of any other size. We must also keep in mind that “up-turned” triangles are impossible to produce with the XOR function, thus cannot be admitted in the “design problem”.
The arrangement of ZTs of k = 1 is generated by a dithered run length pattern {2, 1, 2, 1, …} where the 2s apply to 1-bits, and the 1s to zeros, starting with a singleton 1, ending with a pair of 1s for the lower and vice versa for the upper arrangement. The zeros in T(n) for n in this sequence occur in a hexagonal arrangement, neatly surrounded by 1s (as is the case of all ZTs).
OEIS A334930 lists numbers that produce grain size 1 RSTs, none of which have CZTs.
Figure 8.2 demonstrates that we can use a generating function (1 + 11x + 4x² − 8x³)/(1 − 9x² + 8x4) to generate RSTs that have singleton zeros in a hexagonal matrix of 1-bits:

For grain size 2, we find we cannot place two ZTs in a horizontal line with one another to maintain the grain size, but we can stagger them vertically by an iteration. This gives rise to an irregular infix run length sequence {1,1,2,3}, making for a border that introduces ZTs of side length 1, thus, an impure rendition of grain size 2. Because of this we cannot find “pure” grain size 2 in any RST. We might regard the sort of RSTs produced here as “clipped” versions of a pattern with grain size 2, where the edge conditions are merely interrupted, however, this is an aesthetic viewpoint that stands aside the notion of all ZTs having k = 2.
Figure 8.3 demonstrates an “impure” grain size 2 in RSTs with CZTs, generated by OEIS A334931 = {151, 233, 1483, 1693, 10707, 13029, 644007, 941241, 317049751, 490370281, 3111314891, 3550957213, 22455577043, 27325461221, …}.
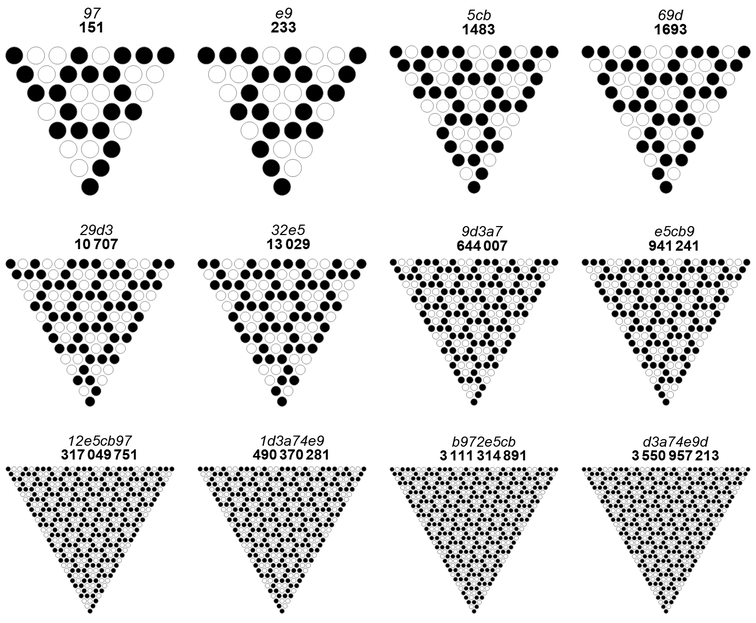
We note that grain size 2 solutions in the above figure represent instances of RSTs with CZTs of frame width and side length (j, 2). The lower form of these trianges has recipe 12113, 1132112, 111231122, 12311231123, 1211321132113, … .
Looking at grain size 2 as a design problem, suppose we were to meld the 1 bits that delimit the run of 2 zeros. This would produce a solid run of 1s in the preceding iteration, therefore, the arrangement is impossible. We could butt the same 1s so as to make for a run length of 2 as we observe in the case of grain size 1. Here, we introduce a singleton 1 in the preceding generation so as to perhaps give rise to the run lengths {1, 1, 3, 1, 3, 1, 3} → n = 6007, {2, 1, 3, 1, 3, 1, 3} → n = 14199, or {3, 1, 3, 1, 3, 1, 3} → n = 30583. Examining these seeds (see Figure 6.6 below) shows that though we might produce a series of 2-ZTs in a horizontal arrangement, we find a singleton 1 nestled between, setting up a dither pattern for m = 2. Since every bit pair in that iteration disagrees, we end up with a solid run of 1s, followed by zeros. The XOR-triangles for these recipes are not rotationally symmetrical. The only way to arrange 2-ZTs is by staggering them as they appear in Figure 8.4.
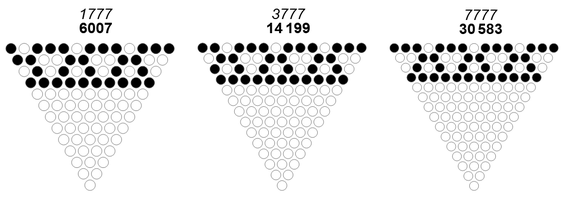
We note that the above pattern in Figure 6.8, by rows, has recipe chain (0) → (11) → (22) → (31), the very same sequence that supports frame width j = 4 in RSTs with a CZT, only missing the prefix and suffix that would make for a rotationally symmetrical T(n). This implies, given a sufficiently long bitstring, that we might identify infix modules that sustain a given frame width without requiring observation of RSTs with CZTs.
Grain size 3 requires staggering ZTs in an interlocking way, generated by run lengths {1, 2}, then {4, 2, 4, 2, …}, then a final 3 (with 4 pertaining to 1s). This renders a CZT impossible, since the prefix forces ZTs off axis from vertex to midpoint (regarding the figure as a triangle). Furthermore, we find that ZTs with k = 2 appear along the edges, thus, Figure 8.5 demonstrates an impure grain size 3, generated by numbers in OEIS A334932:
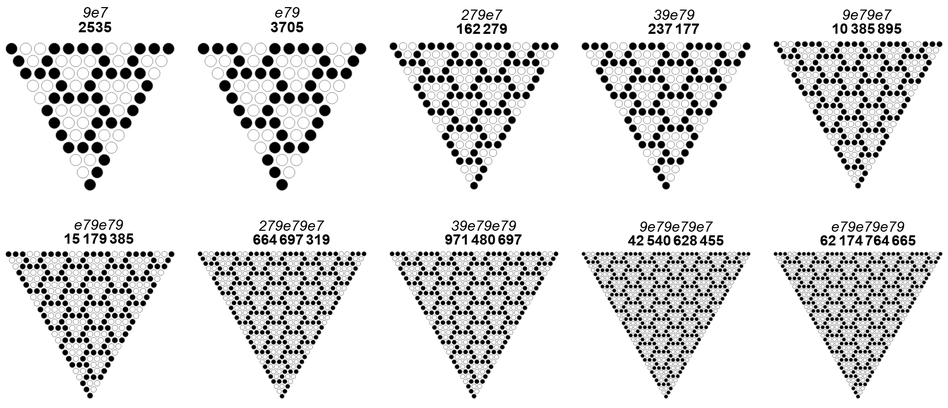
Once again, looking at grain size 3 as a design problem, we find that this is the only arrangement of 3-ZTs that seems to work. We might try run lengths {…, 4, 1, 4, 1, …} to end up with singleton zeros nestled between 3-ZTs and XOR-triangles that are not rotationally symmetrical.
In order to produce an RST of an impure grain size 3 with a central zero-triangle, we must accept more irregularity as seen in Figure 8.1.
Grain size 4 and above would seem to be impossible to construct, looking at it from the standpoint of a design problem, though this is not a proof. Figure 8.6 shows RSTs for n < 325218466199 that have S(n,4) maximum in A333624, i.e., {543, 993, 2439, 3609, 4367, 7697, 156039, 230937, 9986439, 14779929}. Only the first two have CZTs.
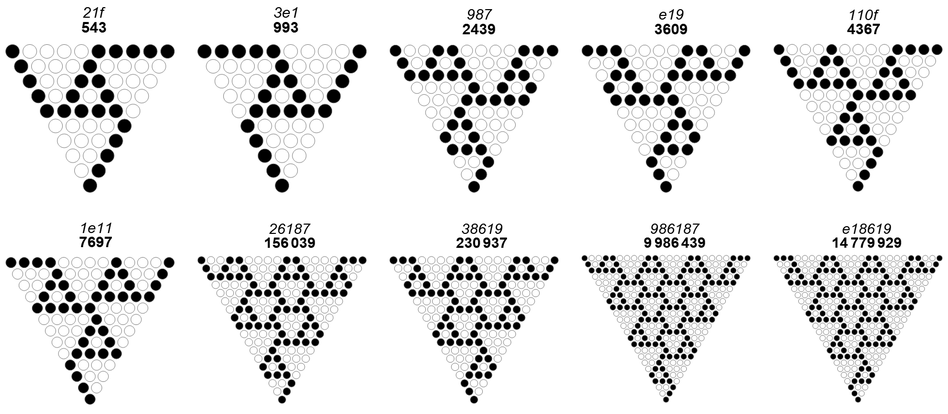
From the last 4 triangles, we observe that run length {…, 4, 2, 4, 2, …} (4 pertaining to 0) breaks down into a field of grain size 3.
No RSTs with CZTs or without could be found with a dominating population of zero-triangles of k > 4, in the list of 10000 terms of A334556 or A334769. However, we can produce a {4, 1} sort of grain, shown in Figure 8.7:
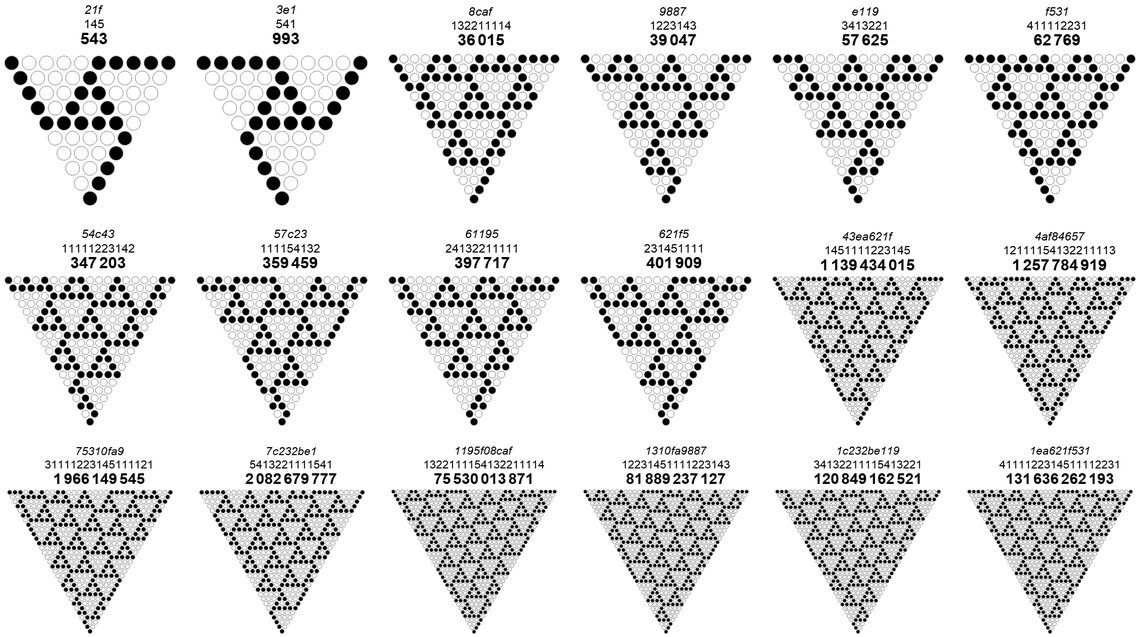
Figure 8.8 shows a {5, 1} grain:
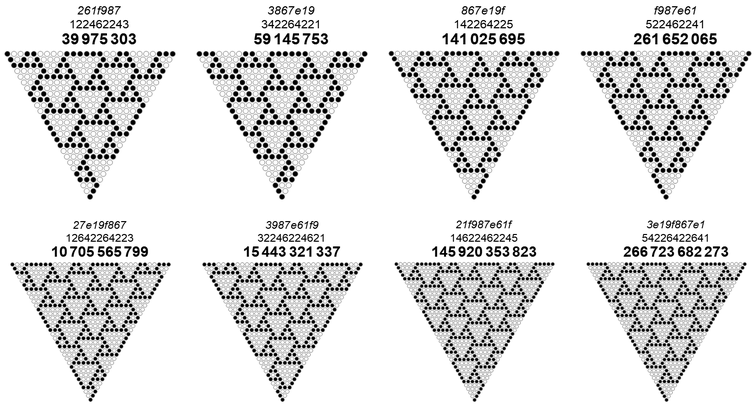
At the point of introducing more complex grain formulations, we might decide that we could go on to produce a multitude of such formulations, admitting other side lengths, ad infinitum. We could undertake to decode their run length recipes and generate sequences that produce these compound grain patterns. Such patterns, clipped only at the edges of the XOR-triangle, appear pleasant to human eyes for their symmetry and regularity, but are perhaps not of general interest.
Rotationally symmetrical XOR-triangles with a “full spectrum” of zero-triangle edge lengths.
In contrast to the notion of a uniform grain size of zero-triangles, we can produce RSTs that have ZTs with edge lengths 1 ≤ k ≤ K. Figure 8.7 shows the smallest n that generate an RST with a full spectrum of ZTs for 1 ≤ K ≤ 7:
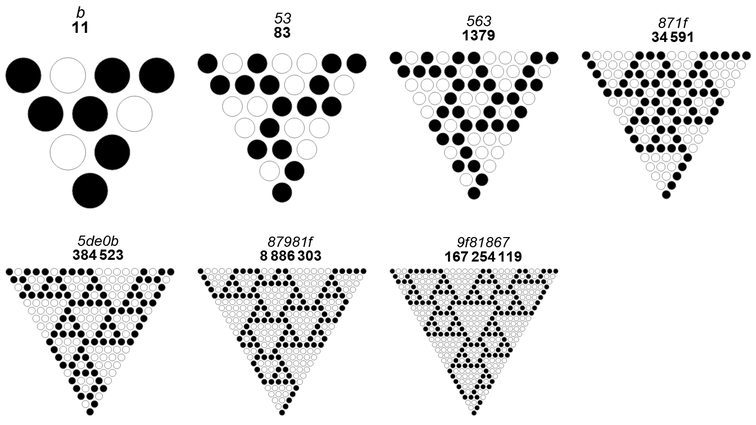
We may note that only K = {3, 4, 5, 7} have CZTs. The smallest n that generate an RST with CZT and a full spectrum of ZTs for 2 ≤ K ≤ 8 appears in Figure 8.8 below:
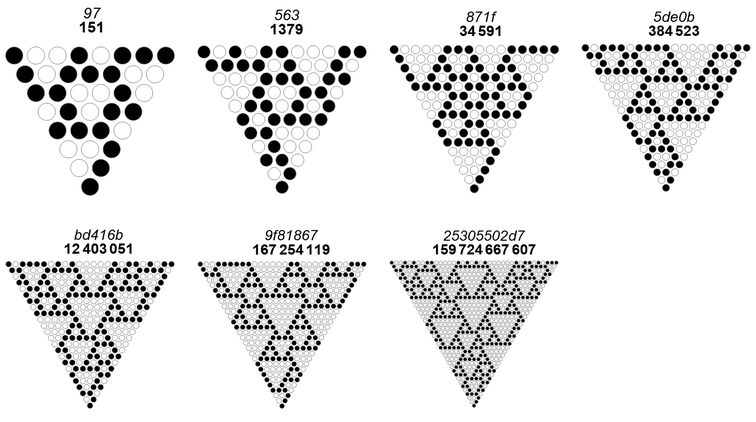
Note that finding an instance of K = 1 for n in A334769 is not possible, since it is tantamount to finding T(n) with grain size 1. We know that grain size one is characterized by a field or matrix of singleton zeros in a hexagonal arrangement that is kept off axis, therefore never generates a central singleton zero. For numbers in A334930 (n that produces RSTs with grain size 1), we have ℓ (mod 3) ≡ 1, always placing a 1-bit at center. Therefore we see K = 1 for RSTs, but when we place the constraint of requiring a center zero-triangle, we cannot satisfy. A334769 and A334930 do not intersect.
It does not seem that we could write a formula to determine the smallest n that exhibits zero triangles in a full range of edge lengths 1…K for the constrained or unconstrained cases, and it is not known whether 159724667607 is the smallest n that has a full spectrum of ZTs for K = 8.
Admission of a number of leading zeros to b(n).
Rémy Sigrist posed sequence A335061, an irregular triangle U(m, i) that pads the left side of b(n) so as to have m bits and allow leading zeros in an XOR-triangle. This sequence issues many aesthetically pleasing arrangements, including the dozen shown below in Figure 9.1 (see an expanded view of 486 such triangles pertaining to n > 0 in rows 3 ≤ m ≤ 20.
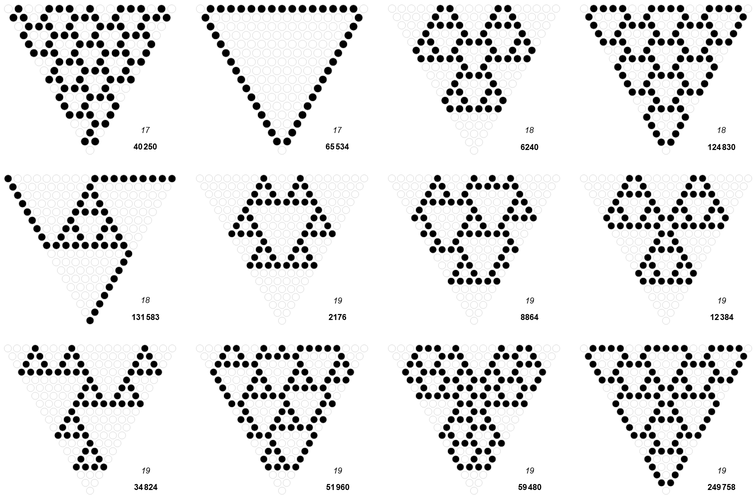
Here we see many familiar arrangements; including grain size 2 for (n, m) = (40250,17), grain size 3 for (124830, 18), and grain (4, 1) for (51960,19). There can be quite large blank areas so as to lend an apparent hexagonal symmetry. We note that frame width j = 1 is possible as at (65534, 17), and indeed any (2x − 2, x + 1). We can indeed have no frame at all, frame width j = 0, meaning a full XOR-triangle of zeros, starting with n = 0 for any value of m. The examination of these shapes is beyond the scope of this work.
The phenomenon of central zero-triangles of XOR-triangles continues to promise much exploration.
Acknowledgements:
Thanks to Peter Kagey for posing sequence A334556, which served as the springboard for these investigations, along with personal correspondence. Thanks as well to Antti Karttunen who in a 7 May correspondence suggested the similarity between XOR-triangles and the Sierpiński and Pascal’s triangles.
Special thanks to Rémy Sigrist, who had corrected the original dataset for A334769 and provided 10,000 terms as well as additional code. Through his help, the author was able to correct the data in this paper.
Code 1.1: A function that generates the bits of an XOR triangle:
xortri[n_] :=
Block[{m, w}, m = IntegerLength[n, 2];
MapIndexed[PadRight[#, m, -1] &,
Set[w, NestList[Map[BitXor @@ # &, Partition[#, 2, 1]] &,
IntegerDigits[n, 2], m - 1]]] /. -1 -> Nothing]
Select[Range[10^4],
Block[{n = #, m, w},
m = IntegerLength[n, 2];
(Reverse /@ Transpose[#] /. -1 -> Nothing) == w &@
MapIndexed[PadRight[#, m, -1] &,
Set[w, NestList[Map[BitXor @@ # &, Partition[#, 2, 1]] &,
IntegerDigits[n, 2], m - 1]]]] &]
Code 1.3: Produce a diagram of T(543):
Block[{n = 543, k = Sqrt[3]/2., t, m, size = 24},
t = NestWhileList[Map[BitXor @@ # &, Partition[#, 2, 1]] &, IntegerDigits[n, 2], Length@ # > 1 &]; m = IntegerLength[n, 2];
Show[Graphics[
Join[{EdgeForm[Directive[Thin, LightGray]]},
Apply[Join,
MapIndexed[
Function[{w, y},
MapIndexed[{If[(Reverse /@
Transpose[MapIndexed[PadRight[#, m, -1] &, t]] /. -1 -> Nothing) == t,
If[#1 == 1, Black, White], Hue[1, 0, 1 - #1/3]],
Disk[2.5 {First[#2] + (y - 1)/2, -k y}]} &, w]] @@ {#1, First[#2]} &, t]],
If[m >= 30,
{Text[Style[n, Bold, FontSize -> size], {5 m/4., 1 m/12.}],
Text[Style[m, Italic, FontSize -> size], {5 m/4., 1 m/4.}]},
{Text[Style[n, Bold, FontSize -> size], {(17 + 2 Boole[n < 512]) m/8., -17 m/8.}],
Text[Style[m, Italic, FontSize -> size], {(17 + 2 Boole[n < 512]) m/8., -15 m/8.}]}]]],
ImageSize -> Large]]
Code 3.1: Generate S(n,k) = A333624:
Array[Function[w, If[Length@ # == 0, {0},
ReplacePart[ConstantArray[0, Max@ #[[All, 1]]],
Map[#1 -> #2 & @@ # &, #]]] /. -Infinity -> 0 &@
Tally@ Flatten@ Array[If[# == 1,
Map[If[First@ # == 1, Nothing, Length@ #] &, Split@ w[[#]] ],
Map[If[First@ # == -1, Length@ #, Nothing] &,
Split[w[[#]] - Most@ w[[# - 1]] ] ]] &, Length@ w]]@
NestWhileList[Map[BitXor @@ # &, Partition[#, 2, 1]] &,
IntegerDigits[#, 2], Length@ # > 1 &] &, 39] // Flatten
Code 4.1: Generate a list of RSTs that have CZTs (i.e., A334769):
Block[{f, s = Rest[Import["https://oeis.org/A334556/b334556.txt", "Data"][[All, -1]] ]},
f[n_] := NestWhileList[Map[BitXor @@ # &, Partition[#, 2, 1]] &,
IntegerDigits[n, 2], Length@ # > 1 &];
Array[Block[{n = s[[#]]}, If[# == 0, Nothing, n] &@
FirstCase[MapIndexed[
If[2 #2 > #3 + 1, Nothing, #1[[#2 ;; -#2]]] & @@ {#1, First[#2], Length@ #1} &,
f[n][[1 ;; Ceiling[IntegerLength[#, 2]/(2 Sqrt[3])] + 3]] ],
r_List /; FreeQ[r, 1] :> Length@ r] /. k_ /; MissingQ@ k -> 0] &, 144, 2] ]
Code 5.1: Generate a list of side lengths k of RSTs that have CZTs (i.e., A334770):
Block[{f, s = Rest[Import["https://oeis.org/A334556/b334556.txt", "Data"][[All, -1]] ]},
f[n_] := NestWhileList[Map[BitXor @@ # &, Partition[#, 2, 1]] &,
IntegerDigits[n, 2], Length@ # > 1 &];
Array[Block[{n = s[[#]]}, If[# == 0, Nothing, #] &@
FirstCase[
MapIndexed[
If[2 #2 > #3 + 1, Nothing, #1[[#2 ;; -#2]]] & @@ {#1, First[#2], Length@ #1} &,
f[n][[1 ;; Ceiling[IntegerLength[#, 2]/(2 Sqrt[3])] + 3]] ],
r_List /; FreeQ[r, 1] :> Length@ r] /. k_ /; MissingQ@ k -> 0] &,
Length@ s - 1, 2] ] ]
Code 5.2: Generate a list of frame widths j of RSTs that have CZTs (i.e., A334796):
Block[{f, s = Rest[Import["https://oeis.org/A334556/b334556.txt", "Data"][[All, -1]] ]},
f[n_] := NestWhileList[Map[BitXor @@ # &, Partition[#, 2, 1]] &,
IntegerDigits[n, 2], Length@ # > 1 &];
Array[Block[{n = s[[#]]},
If[# == 0, Nothing, (1 + Floor@ Log2[n] - #)/3] &@
FirstCase[
MapIndexed[If[2 #2 > #3 + 1, Nothing, #1[[#2 ;; -#2]]] & @@ {#1, First[#2], Length@ #1} &,
f[n][[1 ;; Ceiling[IntegerLength[#, 2]/(2 Sqrt[3])] + 3]] ],
r_List /; FreeQ[r, 1] :> Length@ r] /. k_ /; MissingQ@ k -> 0] &, Length@ s - 1, 2] ]
Code 5.3: Generate a list of the smallest n that generate RSTs with CZTs of a given side length k (i.e., A334771):
Block[{f, s = Rest[Import["https://oeis.org/A334556/b334556.txt", "Data"][[All, -1]] ], t, u},
f[n_] := NestWhileList[Map[BitXor @@ # &, Partition[#, 2, 1]] &,
IntegerDigits[n, 2], Length@ # > 1 &];
Set[{t, u}, Transpose@ Array[Block[{n = s[[#]]}, If[# == 0, Nothing, {n, #}] &@
FirstCase[MapIndexed[
If[2 #2 > #3 + 1, Nothing, #1[[#2 ;; -#2]]] & @@ {#1, First[#2], Length@ #1} &,
f[n][[1 ;; Ceiling[IntegerLength[#, 2]/(2 Sqrt[3])] + 3]] ],
r_List /; FreeQ[r, 1] :> Length@ r] /. k_ /; MissingQ@ k -> 0] &, Length@ s - 1, 2]];
Array[If[! IntegerQ@ #, 0, t[[#]] ] &@ FirstPosition[u, #][[1]] &, Max@ u] ]
Code 5.4: Efficiently generate a list of the smallest n that generate RSTs with CZTs of a given side length k (i.e., A334771):
LinearRecurrence[{0, 0, 0, 17, 0, 0, 0, -16},
{543, 151, 2359, 599, 8607, 2391, 37687, 9559}, 10^4]
Code 6.1: Generate A334930, a list n that generate RSTs with ZTs of grain size 1:
CoefficientList[Series[(1 + 11 x + 4 x^2 - 8 x^3)/(1 - 9 x^2 + 8 x^4), {x, 0, 36}], x]
Code 6.2: Generate A334931, a list n that generate RSTs with ZTs of grain size 2 (accepting edge artifacts):
Array[FromDigits[Flatten@ MapIndexed[
ConstantArray[#2, #1] & @@ {#1, Mod[First[#2], 2]} &,
If[EvenQ@ #1, Reverse@ #2, #2]], 2] & @@
{#1, Which[#2 == 1,
PadRight[{1, 2}, 12 Ceiling[#1/8] - 7, {3, 2, 1, 1}], #2 == 2,
PadRight[{1, 1}, 12 Ceiling[#1/8] - 6, {1, 1, 3, 2}]~Join~{2}, #2 == 3,
PadRight[{1, 1}, 12 Ceiling[#1/8] - 4, {3, 1, 1, 2}]~Join~{2},
True, PadRight[{}, 12 Ceiling[#1/8] - 1, {1, 2, 3, 1}]]} & @@
{#, Ceiling[Mod[#, 8]/2]} &, 24]
Code 6.3: Generate A334932, a list n that generate RSTs with ZTs of grain size 3 (accepting edge artifacts):
Array[FromDigits[Flatten@ MapIndexed[
ConstantArray[#2, #1] & @@ {#1, Mod[First[#2], 2]} &,
If[EvenQ@ #1, Reverse@ #2, #2]], 2] & @@
{#, Join[{1, 2}, PadRight[{}, Ceiling[#, 2], {4, 2}], {3}]} &, 24]
Concerns sequences:
A030101: Binary integer reversal of n: reverse the bits of n to create n′.
A070939: a(0) = 0; a(n) = 1 − ⌊log2 n⌋: binary integer length of n.
A101211:
R(n,k) is the k-th run length found in the binary expansion b(n).
A318927: Concatenation of terms in row n of A101211.
A333624: Irregular triangle S(n,k) enumerating the number of zero-triangles with side-length k in T(n).
A333625: Interpret row m = S(m,k) for m in A334556 as row m in A067255.
A334556: Numbers whose binary expansion generates rotationally symmetric XOR-triangles (RSTs).
A334596: Number of values m in A334556 with binary length A070939(m) = n.
A334769: Numbers whose binary expansion generates RSTs with central zero-triangles (CZT).
A334770: a(n) = side length k of CZTs in the RSTs of A334769(n).
A334771: Smallest numbers m that generate a CZT of side length n in an RST.
A334796: a(n) = frame width j of CZTs in the RSTs of A334769(n).
A334836: Smallest numbers m that generate a CZT of frame width n in an RST.
A334896: Interpret row m = S(m,k) for m in A334769 as row m in A067255.
A334930:
RSTs that have singleton zeros in a hexagonal matrix.
A334931:
RSTs that have an impure grain size 2.
A334932:
RSTs that have an impure grain size 3.
A335061: Irregular triangle U(m, i) of RSTs that admit a number of leading zeros to b(n) so as to furnish an m-bit seed.
A335077:
RSTs for n that set records for the side length k of zero-triangles (not necessarily central).
References.
[1] “DSM” MathOverflow user, Number triangle, 2 May 2020.
[2] Larry Riddle, Binary Description of the Sierpinski Gasket, Classic Iterated Function Systems, Agnes Scott College, 1998-2020.
[3] Wolfram Mathworld (Eric W. Weisstein), Sierpiński Sieve.
[4] Stephen Wolfram, Oh My Gosh, It’s Covered in Rule 30s!, Writings, 2017.
Document Revision Record.
2020 0508 1200 Created.
2020 0512 1530 Publication.
2020 0513 1645 Refined examination of linear recurrences.
2020 0514 1200 Update, add hexadecimal notation that facilitates perception of bit-patterns.
2020 0515 0830 Add Karttunen's 0507 correspondence, connection with Sierpiński and Pascal.
2020 0515 1730 Corrections based on Rémy Sigrist's dataset.
2020 0516 1600 Grain size observations.
2020 0517 2115 Run length recipes, infix module tree.
2020 0518 1700 Expanded run length recipe section, corrected tree.
2020 0521 1800 Enlarged and verified tree.
2020 0522 1700 Added reference to MathOverflow, A335077.
2020 0524 2200 Added observations related to A335061.