Constitutive Functions Glossary

Home Glossary

The constitutive arithmetic functions

Let k and n be nonzero positive integers, and let primes p | n and q be a nondivisor of n, thus coprime to n. We recognize the Fundamental Theorem of Arithmetic (the unique factorization theorem) and the standard form of prime decomposition of a number [1, 2, 3].

In this work, the term “constitutive arithmetic relationship” refers to one of three mutually exclusive states (apart from the number 1) of k with respect to n. These are n-regular, n-semicoprime, or n-coprime, with the number 1 both regular and coprime to n. The relationships are constitutive because they depend on the constituent prime factors of both numbers.

Links to sections:

1. Three classes
2. Infinite classes
3. Counting functions
4. Applications to number bases
5. Coinage of the term
6. References

Three possible relationships

(Back to top ↑)

There are only three possible constitutive arithmetic relationships between k and n. We recognize that primes must either divide an integer or are coprime to the number if not a divisor [4]. Therefore we have evidence of two possible states, one of which, the coprime state, is one wherein gcd(n, k) = 1, that is, k and n have no prime factor in common [5, 6]. We know that the product of coprime numbers is also coprime [7]. It follows that the product of two numbers that each have no prime factors q indeed remains without any q as a factor. Therefore we can produce three cases that apply to composite numbers:

pp,         pq,           qq.

The first case we call n-regular [8]. An n-regular number r divides some perfect power n^ε with ε ≥ 0. It is clear that the divisor is a special case of n-regular number such that d | n^ε with 0 ≤ ε ≤ 1. The number d = 1 divides all n since 1 | n⁰. Therefore, p is regular to n since it divides n. In this work we call nondivisor n-regular numbers “semidivisors” of n. A semidivisor r | n^ε with ε > 1. In this work, we refer to ε as the richness of n-regular r.

The second case is necessarily composite since it is the product of at least one prime p | n and at least one nondivisor prime q. In this work, we refer to this case as the n-semicoprime s. An n-semicoprime number k is nonregular and noncoprime to n; in this work therefore, we say that n-semicoprime s is neutral to n. We call n-semicoprime s such that s < n a “semitotative” of n, in line with the n-coprime t < n being referred to as totatives. We can express n-semicoprime numbers s as a product of a regular factor and a coprime factor.

s = r × t

Finally, we have the third n-coprime case t. An n-coprime number k has no prime factor in common with n. Like n-regular numbers, n-coprime numbers can be prime or composite.

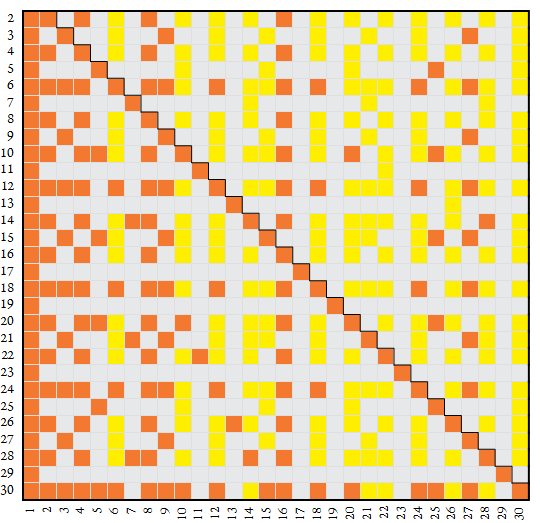
The map below shows constitutive relationships between number base n appearing on the vertical axis and digit k appears on the horizontal. The n-regular k appear in orange (■), n-semicoprime k appear in yellow (■), and n-coprime k > 1 appear in light gray (■). The number k = 1 is both regular and coprime, but in the map 1 is shown in orange.

Infinite classes pertaining to the squarefree root of n

(Back to top ↑)

For n > 1, the number of n-regular r is infinite. There are a finite number of distinct prime divisors p | n [10, A001221], yet we can produce n-regular numbers r with no p at all (since 1 is the empty product), or any number of p with multiplicity. We can produce the n-regular n as a tensor product R of the prime power ranges p^m , with m ≥ 0; all such products k are unique and therefore we can sort them. Thus, the cardinality of R is aleph-0. For n = 1, the only n-regular number r = 1 since 1 is the empty product; all primes are coprime to 1.

For all n, the number of n-coprime t is infinite. All primes q > n are coprime to n and there may be some primes q < n also coprime to n. Since the number of primes is infinite with cardinality aleph-0 and all nondivisor primes q are coprime to n, almost all primes are coprime to n. We can also produce n-coprime numbers t with no q at all (since 1 is the empty product), or any number of q with multiplicity. Here we see that 1 is both regular and coprime to n. Thus, the cardinality of T is aleph-0. For n = 1, all k are n-coprime since 1 is the empty product; all primes are coprime to 1.

For n > 1, the number of n-semicoprime s is infinite. So long as we have at least one p and at least one q as factors, we may select or repeat any p or q as additional factors to get an n-semicoprime product s. Again is S sortable since all the possible products are unique, thus S has cardinality aleph-0. For n = 1, there are no 1-semicoprime numbers.

Numbers that have arithmetic relationship to the squarefree kernel rad(n) have the same relationship to any number with the same set of distinct prime factors of rad(n). In other words, each of the constitutive classes pertains to the distinct prime divisors p of n regardless of their multiplicity. Because of this, R, S, and T pertain to the squarefree kernel of n. For instance, the set of numbers {1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, …} [10, A003586] are regular to 6, but also to 12, 18, 24, 36, 48, 72, etc.; any of the numbers in the set are regular to any multiple of 6. The Hamming numbers {1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, …} [10, A051037] are regular in any n that has all of {2, 3, 5} as distinct prime divisors.

Constitutive counting functions

(Back to top ↑)

We can create counting functions by applying a bound to k related to n and assessing how many k are regular, semicoprime, or coprime.

The Euler totient function is most inherent and well-known [10: A000010]. We might also refer to the function as the totative counting function, as it is the number of k < n coprime to n. Such numbers are called totatives or reduced residues t of n. Given the standard prime power decomposition of n:

φ(n) = n × Π (1 − 1/p)                                                          
= n ×(1 − 1/p₁) ×(1 − 1/p₂) × … × (1 − 1/p_i) [11]

We note that φ(n)/n = Π (1 − 1/p), the totient ratio, is only dependent on the distinct prime divisors p | n but not their multiplicities ε. The totient ratio is shared among numbers n that have the same squarefree kernel. For example, φ(6)/6 = φ(12)/12 = 1/3, in other words, one third of the numbers 1 ≤ k ≤ n are coprime to n. Likewise, φ(10)/10 = φ(20)/20 = 2/5, φ(2)/2 = φ(4)/4 = φ(8)/8 = φ(16)/16 = 1/2. The chart below illustrates the totient ratio for squarefree n. The vertical axis represents the totient ratio φ(m)/m, 0 at bottom and 1 at top, while the horizontal represents the number of distinct prime divisors of squarefree m. On the chart, we can find the totient ratio for any n by finding the point representing φ(m)/m, where m is the squarefree kernel of n. [10: A307540]. The higher the totient ratio φ(n)/n, the greater the chance that an arbitrary nonzero positive integer k is coprime to n.

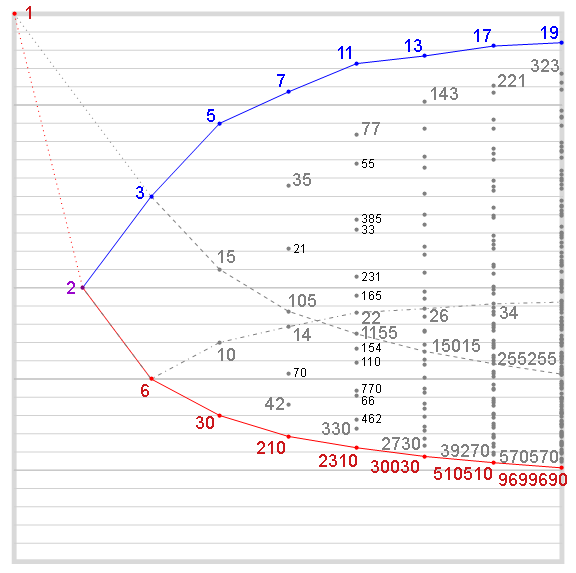
The reduced residue system (RRS) of n contains all the totatives t of n. For example, RRS(10) = {1, 3, 7, 9}. Given the RRS, we can determine all n-coprime numbers using congruency. A number k is coprime to n if k mod n ≡t. Any number k = ±1 (mod n) is coprime to n since 2 is the smallest prime [12]. Since the RRS is indicative of n-coprime numbers by congruence, the application of n as a bound for an n-coprime counting function makes sense.

The divisor counting function τ(n) is similarly inherent and well-known [10: A000005]. No divisor d can exceed n, thus the number of divisors is finite and a bound at n makes sense regarding this special case of n-regular r. Given the standard form prime power decomposition of n:

τ(n) = Π (ε + 1)                                            
= (ε₁ + 1) × (ε₂ + 1) × … × (ε_i + 1)

The regular counting function RCF(n) is less-well known [10: A010846] and not as easy to compute. (See this page for detail on the function and efficient computation.) The bounding of the function τ(n) to include d ≤ n is natural, since divisors cannot exceed n. It is less natural perhaps to consider the regular numbers r ≤ n, since there are an infinite number of semidivisors larger than n. There are some interesting properties of RCF(n) that perhaps underscore a purpose for the bound. Primes n = p and perfect prime powers n = p^ε do not have semidivisors r < n. Numbers 1 ≤ k ≤ p must either divide or be coprime to p in the first case, and all regular 1 ≤ k ≤ p^ε, are divisors in the second case as they are themselves perfect prime powers p^m with 0 ≤ m ≤ ε. Of course, n itself is n-regular, and as stated, divisors, a special case of n-regular number, may not exceed n. For this reason, people have determined a motivation to create a counting function for regulars r ≤ n.

We might derive a semidivisor counting function ξ_d(n) that counts nondivisor regulars r < n:

ξ_d(n) = RCF(n) – τ(n),
   = ξ(n) − ξ_t(n)

or in terms of the OEIS:

A243822(n) = A010846(n) − A000005(n),
                    = A045763(n) − A243823(n)

The bound at n does not seem as useful as regards semidivisors but for the fact that divisors, the other class of n-regular numbers, is indeed effectively bounded at n. The range 1 ≤ ξ_d ≤ n does have some interesting properties. (See this page for details.)

Given the Euler totient function and the regular counting function, we can determine the semicoprime counting function, which we instead call the semitotative counting function ξ_t(n) [10: A243823].

ξ_t(n) = n − (RCF(n) + φ(n) − 1),
   = ξ(n) − ξ_d(n)               

or in terms of the OEIS [10]:

A243823(n) = n − (A010846(n) + A000010(n) − 1),
                  = A045763(n) − A243822(n)

The bound at n seems least useful as regards n-semicoprime s but for the fact that the bound makes at least some sense for the other two constitutive classes. The range 1 ≤ s ≤ n does have some interesting properties. (See this page for details.)

We can combine the semidivisor and semitotative counting functions to produce a “neutral counting function” that counts numbers 1 ≤ k ≤ n that are not counted by neither the divisor counting nor the Euler totient function. Indeed this is [10: A045763], which is fairly easy to calculate:

ξ(n) = n − (τ(n) + φ(n) − 1)
= ξ_d(n) + ξ_t(n)      

or in terms of the OEIS:

A045763(n) = n − (A000005(n) + A000010(n) − 1)      
= A243822(n) + A243823(n)

The range 1 ≤ ξ ≤ n does have some interesting properties. (See this page for details.)

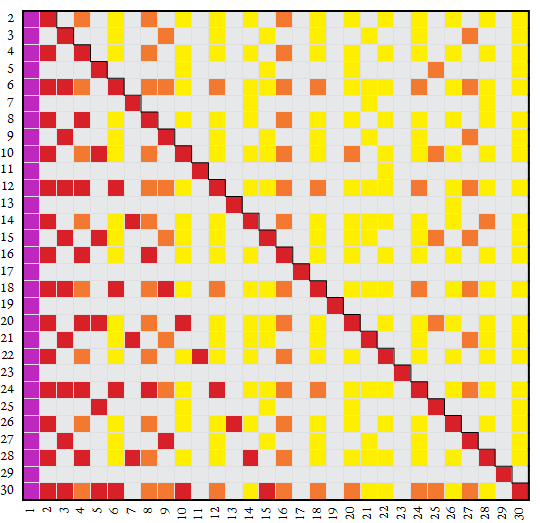
Since the counting functions break the constitutive classes into easily constructible subcomponents, we can thus produce the following map. The map below shows number base n appearing on the vertical axis and number k on the horizontal. Divisors d > 1 appear in red (■) and nondivisor n-regular k (semidivisors) appear in orange (■), n-semicoprime k appear in yellow (■), and n-coprime k > 1 appear in light gray (■). The number k = 1 is both regular and coprime and appears in purple (■).

Applications of constitutive arithmetic functions in base n

(Back to top ↑)

Aside from arithmetic itself, the constitutive relationships govern the behavior of the expansion of fractions and certain divisibility tests, [13, 14]

An n-regular r | n^ε as denominator of fraction m/r, with m an integer, enjoys a terminating base-n expansion that has ε digits after the radix point. Examples: in decimal, 2 | 10, and 1/2 = .5; in base 12, 16 | 12² and one sixteenth is written “.09”. The base-n regular divisibility test involves examining the last ε digits D of an arbitrary nonzero positive integer x to determine if D appears among n^ε/r combinations. Examples: in decimal, we know that 125 is divisible by 5 since the last digit is one of 2 combinations, {0, 5}. In tetradecimal (base 14), we know that “c37” is divisible by “37”, since it ends in one of 4 combinations {“00”, “37”, “70”, “a7”} (decimally we are saying 7⁴ is divisible by 7²).

An n-coprime t as denominator of fraction m/t, with m an integer, suffers a purely recurrent expansion in base n.

However, if t | (n − 1), the period of the expansion is 1 (it is an omega factor), or if t | (n + 1), the period is 2 (here called an alpha factor).

For instance, in decimal, 3 | (10 − 1) and 1/3 = .333…[15]. In octal, 3 | (8 + 1) so 1/3 = “.494949…”. In duodecimal, 5 divides neither 11 nor 13, and we observe 1/5 = “.24972497…” If t | (t − 1), we may use the digit sum (omega) divisibility test. If we add all the digits of a number x together and the sum is clearly a multiple of t, x is divisible by t as well. In decimal this is familiar as the Rule of 3 and 9. In base 16, the same rule applies instead to 3, 5, and 15.

If t | (n + 1), we may use the alternating sum (alpha) divisibility test. Decimally the alpha test pertains to 11, where it is rather rarely used. We know, for example, that decimal 14762 is divisible by 11 since (1 + 7 + 2) − (4 + 6) = 10 − 10 = 0; 0 is a multiple of 11. (14762 = 11⁴ + 11².) [16] The alpha test would be perhaps more useful in octal and tetradecimal (base 14) where it pertains to 3. There are further tests for certain n-coprime numbers t, but most such numbers do not have an easy and intuitive test.

The ease of use and particular behavior of the omega and alpha numbers and their factors are important enough to merit their general recognition across all number bases n. Note that the number 2 in odd bases is a factor of both omega (n − 1) and alpha (n + 1), but we may use the briefer and more efficient omega tests to determine evenness or parity. We might thus necessitate adding them to the general map, where they additionally show in pale blue (■) and pale green (■), with 2 in an odd base in lavender (■). Therefore the simpler maps in this work show these particular entities. Examination of the map perhaps can lend a cursory understanding about a particular number base regarding the smallest and most useful numbers.

An n-semicoprime s = r × t (where r | n^ε) as denominator of fraction m/t, with m an integer, has a mixed recurrent expansion in base n. This expansion starts right of the radix point with ε nonrepeating digits followed by a recurrent set of digits whose period derives from that of t. We may combine certain divisibility tests that pertain to r and t to devise a compound test for s. An example is the decimal test for 6 = 2 × 3.

The constitutive classifications are helpful in understanding the aggregate behavior of number bases n as regards human application as a tool.

Provenance of the term “constitutive”

(Back to top ↑)

The term “constitutive” is used in this work on account of the pre-eminent governance of the behavior of multiple basic applications of base n, including its arithmetic. The term was selected in order to best describe the arithmetic functions as a group, that they pertain to the constituent distinct prime divisors of a number n. It avoids the re-use of terms like “cardinal”, “general”, etc. that have many meanings in mathematics. The term was coined 7 February 2019. Prior to this date, in earlier manifestations of this work, specifically the October 2012 glossary, the term “cardinal” was used.

References

(Back to top ↑)

References are provided primarily to book sources to amplify research and your web searches in addition to the links to internet sources provided in the glossary. See the site reference list for general book sources and ISBNs. The books are generally deeper and handier to those interested in the subject, complete with exercises for broader understanding of the concepts herein and throughout this work.

[1] Hardy & Wright 2008, Chapter I, “The Series of Primes”, Section 1.3, “Prime numbers”, page 3, specifically: “Theorem 2. (The fundamental theorem of arithmetic) The standard form of n is unique; apart from rearrangement of factors, n can be expressed as a product of primes in one way only”, and the proof at Chapter II, “The Series of Primes”, Sections 2.10, “Proof of the fundamental theorem of arithmetic”, and 2.11, “Another proof of the fundamental theorem of arithmetic”, pages 25−26.

[2] Dudley 1969, Section 2, “Unique factorization”, page 18, specifically: “From the unique factorization theorem it follows that each positive integer can be written in exactly one way in the form n = p₁^e1 × p₂^e2 × … × p_k^ek where e_i ≥ 1, i = {1, 2, … k}, each p_i is a prime, and p_i ≠ p_j for i ≠ i. We called this representation the prime-power decomposition of n, and whenever we write n = p₁^e1 × p₂^e2 × … × p_k^ek it will be understood, unless specified otherwise, that all the exponents are positive and the primes are distinct”.

[3] Dudley 1969, Section 2, “Unique factorization”, page 10, specifically: “A prime is an integer that is greater than 1 and has no positive divisors other than 1 and itself”.

[4] Ore 1948, Chapter 4, “Prime Numbers”, page 50, specifically: “Lemma 4-1. A prime p is either relatively prime to a number or divides it” and ensuing proof.

[5] Hardy & Wright 2008, Chapter V, “Congruences and Residues”, Section 5.1, “Highest common divisor and least common multiple”, page 58, specifically: “If (a, b) = 1, a and b are said to be prime to one another or coprime. The numbers a, b, c, …, k are said to be coprime if every two of them are coprime. To say this is to say much more than to say that (a, b, c, …, k) = 1, which means merely that there is no number but 1 which divides all of a, b, c, …, k. We shall sometimes say ‘a and b have no common factor’ when we mean that they have no common factor greater than 1, i.e. that they are coprime.”

[6] Jones & Jones 2005, Chapter 1, “Divisibility”, Section 1.1, “Divisors”, page 10, specifically: “Definition: Two integers a and b are coprime (or relatively prime) if gcd(a, b) = 1 … More generally, a set of integers a₁, a₂, … are coprime if gcd(a₁, a₂, …) = 1, and they are mutually coprime if gcd(ai, aj) = 1 whenever i ≠ j. If they are mutually coprime then they are coprime (since gcd(a₁, a₂, …) | gcd(a₁, a₂)), but the converse is false.”

[7] LeVeque 1962, Chapter 2, “The Euclidean Algorithm and Its Consequences”, Section 2−2, “The Euclidean algorithm and greatest common divisor”, page 24, specifically: “(e) if a given integer is relatively prime to each of several others, it is relatively prime to their product.” and the ensuing example.

[8] Ore 1948, Chapter 13, “Theory of Decimal Expansions”, page 316, specifically: “In general, let us say that a number is regular with respect to some base number b when it can be expanded in the corresponding number system with a finite number of negative powers of b. … one concludes that the regular numbers are the fractions r = p/q, where q contains no other prime factors other than those that divide b.”

[9] Hardy & Wright 2008, Chapter IX, “The Representation of Numbers by Decimals”, Section 9.3, “Representation of numbers in other scales”, pages 144−145, specifically, Theorem 136. *

[10] Sloane, Neil, The On-Line Encyclopedia of Integer Sequences, Retrieved June 2019.

[11] Jones & Jones 2005, Chapter 5, “Euler’s Function”, Section 5.2, “Euler’s function”, 85-89.

[12] LeVeque 1962, Chapter 1, “Foundation”, Section 1−3, “Proofs by Induction”, pages 11−12, specifically: “For every positive integer n, n and n + 1 have no common factor greater than 1” and the ensuing proof.

[13]Marc Renault, Stupid Divisibility Tricks, (See PDF), Math Horizons (2006). Retrieved in June 2019.

[14]Maths Is Fun, Divisibility Rules. Retrieved in June 2019.

[15] Hardy & Wright 2008, Chapter IX, “The Representation of Numbers by Decimals”, Section 9.6, “Tests for divisibility”, page 147, specifically: “Next 10ν ≡ 1 (mod 9) for every ν, and therefore A₁.10^s + A₂.10^{(s − 1)} + … + A_s.10 + A_{(s + 1)} ≡ A₁ + A₂ + … + A_{(s + 1)} (mod 9). A fortiori this is true mod 3. Hence we obtain the well-known rule ‘a number is divisible by 9 (or by 3) if and only if the sum of its digits is divisible by 9 (or by 3)’.”

[16]Hardy & Wright 2008, Chapter IX, “The Representation of Numbers by Decimals”, Section 9.6, “Tests for divisibility”, page 147, specifically: “Since 10 ≡ −1 (mod 11), we have 10^2r ≡ 1, 10^2r + 1 ≡ −1 (mod 11), so that A₁.10^s + A₂.10^{(s − 1)} + … + A_s.10 + A_{(s + 1)} ≡A_{(s + 1)}− A_s + A_{(s − 1)} … (mod 11). A number is divisible by 11 if and only if the difference between the sums of its digits of odd and even ranks is divisible by 11.”

* Note: there is an error in Theorem 136 regarding the number of digits in a terminating fraction: the counterexample is the base-16 representation of 1/8 = .4 hexadecimally: a single terminating digit. By the Theorem as published, one is led to think that, any expansion of n-regular fractions x/r for r | n^ε with ε > 0 will terminate after something other than ε digits. Suppose n = 16, r = 8, and x = 1. Then, since 8 = 2³ and max(3) = 3, we would have 3 digits after the radix point, which is clearly contradicted by hexadecimal 1/8 = .4. We recognize that the number of digits a terminating fraction 1/k has in base n is the richness ε of n-regular k.

(Back to top ↑)

This page last modified Friday 28 June 2019.
Copyright © 2019 Michael De Vlieger