On sequences beginning with 1 and the first ℓ odd primes and thereafter pairwise coprime between the (ℓ−1) most recent terms.
A085229 is a sequence by Reinhard Zumkeller (2003 0622), while A352849 is by Michael De Vlieger and A352950 is by David Sycamore.
This page written by Michael Thomas De Vlieger, St. Louis, Missouri, 2022 0424.
Abstract.
We examine the effect of recursive coprimality with the previous ℓ terms on parity of k and divisibility of k by 3. We introduce a conjecture regarding a sequence Sℓ and products involving all primes p ≤ ℓ.
Introduction.
Consider a sequence S starting with 1 and the first ℓ odd primes, and consider that, in order to obtain the next term k, we would require k to be the smallest missing number that is pairwise-coprime to the last ℓ terms. The effect of selecting odd primes is that we force prime p = 2 out of its expected order among primes in the sequence S. Does such a sequence generate a permutation of natural numbers? Is there any cyclical behavior in the sequence?
A085229: Case ℓ = 1.
The simplest case of these sequences is Zumkeller’s A085229. Let A = A085229, with A(1) = 1, thereafter, A(n) = least k ∈ ℕ ∧ k ∉ A pairwise-coprime to n and A(n−1).
This is a lexically earliest sequence (LES) of recursive mappings of function f(m) → k, starting with seed {1} ∪ Prime(2…2+ℓ−1) : ℓ = 1, where m = lcm(A(n−1…n−ℓ)) = A(n−1). The function f as Zumkeller defined is as follows:
f(m) → k : k ∈ ℕ ∧ k ∉ A(1…n−1) ∧ k ⊥ n ∧ k ⊥ A(n−1) ∧
(K ∈ ℕ ∧ K ∉ A(1…n−1) ∧ K ⊥ n ∧ K ⊥ A(n−1)) ∧ K > k.
We simplify the definition using m and seed terms {1, 3}:
f(m) → k : k ∈ ℕ ∧ k ∉ A(1…n−1) ∧ k ⊥ m ∧
(K ∈ ℕ ∧ K ∉ A(1…n−1) ∧ K ⊥ m ∧ K > k.
The sequence begins as follows (See Code 1 and Figure 1):
1, 3, 2, 5, 4, 7, 6, 11, 8, 9, 10, 13, 12, 17, 14, 15, 16, 19, 18, 23, 20, 21, 22, 25, 24, 29, 26, 27, 28, 31, 30, 37, 32, 33, 34, 35, 36, 41, 38, 39, 40, 43, 42, 47, 44, 45, 46, 49, 48, 53, 50, 51, 52, 55, 54, 59, 56, 57, 58, 61, 60, 67, 62, 63, 64, ...
Since A is LES, we see the following axioms:
Lexical Axiom: A(n) = k : k ∈ ℕ ∧ k ∉ A(1…n−1).
Earliest Axiom:
If K > k and K also satisfies the other axioms, A(n) = k.
Coprimality Axiom: A(n) = k ⊥ m : m = A(n−1)
Consider a characteristic of all lexically earliest sequences. That is, the range of A(n) = k is divided into 3 intervals:
1. The saturated zone k < u. Here, k ∈ A(1…n−1), hence there is no need to consider such k.
2. The open zone k > r. Here, k ∉ A(1…n−1) by definition of record r. Therefore, iff we arrived at k through a greedy algorithm, i.e., satisfying all the other axioms and approaching from below, then A(n) = k.
3. The mixed zone u ≤ k < r. If we arrived at m through a greedy algorithm, we have to test whether k ∈ A(1…n−1). If false, A(n) = k. We may include r in this zone, though we know if k = r, then k ∈ A(1…n−1) and is banned from a second entry into A.
Theorem A1: 2 | A(2k+1) for k > 0.
Proof A1: consequence of the lexically earliest and coprimality axioms. Even numbers appear in order as a consequence of the latter axiom and since numbers are either even or odd. ∎
Corollary A1.1: the only fixed point is A(1) = 1.
Theorem A2: Generally, if prime p | A(n) then p ⊥ A(n±1).
Proof A2:
Consequence of coprimality axiom. ∎
For p = 2, 2 | A(2k+1) for k > 0 since 2 is the smallest prime. For odd p it is not necessarily true that given p | A(n) ⇒ p | A(n+2) ∨ p | A(n−2), since there may be M < m such that (A(n−1), M) = 1, q | M for prime q < p, and is not in A(1…n−1).
For these reasons, if we also set A(2) = 3, then we need not also check (n, A(n)) = 1, since it isn’t possible. If we do not check (n, A(n)) = 1 and set A(2) = 3, 2 would follow 1 since 1 is coprime to all numbers.
Theorem A3: 3 | A(3k+1) for k > 1.
Proof A3: For even k, 6 | A(3k+1), i.e., 6 | A(n) : n mod 6 ≡ 1, and it is easy to see that since even numbers appear in order in the sequence, these even multiples of 3 are also in order. Because 3 | A(n) : n mod 6 ≡ 1, we cannot have 3 | A(n) for n ≡ 0 ∨ n ≡ 2 (mod 6). Furthermore, we know that 2 | A(n) for n ≡ 3 ∨ n ≡ 5 (mod 6). So 3 | A(n) odd : n mod 6 ≡ 4, that is, 3 | A(3k+1) for k > 1. ∎
Corollary A3.1: 6 | A(6k+1) = 6k.
Theorem A4: Odd primes q set records.
Proof A4: q ⊥ A(n−1) as a consequence of lexically earliest axiom that rules out equality, and by the definition of prime. 2 is displaced on account of the axiom that bans equality between n and A(n). Therefore, whereupon q is the smallest unused odd number, it enters the sequence. ∎
A consequence of Theorems 1 and 3 is that 2δ and 3ε : ε > 1 do not set records, since their adjacency is governed by A(n−1). The powers of other primes do set records since coprimality does not depend on multiplicity.
The smallest composite record is A(24) = 25. Smallest record m with ω(m) > 1 is A(54) = 55. Powers of 2 and 3 are absent from records for n ≤ 2²⁰.
These theorems show that divisibility by 2 is strictly governed by the coprimality and lexically earliest axioms, while divisibility by 3 is less strictly governed yet confined to antipodes (mod 6).
A352849: Case ℓ = 2.
Now we turn to the intermediate case A352849, which is the same as A085229 but setting ℓ = 2. We expect this sequence to share properties with Zumkeller’s A084937, which starts with {1, 2}.
Let B = A352849, with B(1) = 1, thereafter, B(n) = least k ∈ ℕ ∧ k ∉ B pairwise-coprime to n, B(n−1), and B(n−2).
This is also a lexically earliest sequence (LES) of recursive mappings of function f(m) → k, starting with seed {1} ∪ Prime(2…2+ℓ−1) = {1, 3, 5} : ℓ = 2, where m = lcm(A(n−1…n−ℓ)). The function f is defined below:
f(m) → k : k ∈ ℕ ∧ k ∉ B(1…n−1) ∧ k ⊥ m ∧
(K ∈ ℕ ∧ K ∉ B(1…n−1) ∧ K ⊥ m ∧ K > k.
The sequence begins as follows (See Code 2 and Figure 2):
1, 3, 5, 2, 7, 9, 4, 11, 13, 6, 17, 19, 8, 15, 23, 14, 25, 27, 16, 29, 21, 10, 31, 33, 20, 37, 39, 22, 35, 41, 12, 43, 47, 18, 49, 53, 24, 55, 59, 26, 45, 61, 28, 51, 65, 32, 57, 67, 34, 63, 71, 38, 69, 73, 40, 77, 79, 30, 83, 89, 36, 85, 91, 44, 75, 97, 46, 81, ...
Set the smallest missing number u : u ∈ ℕ ∧ u ∉ B(1…n−1).
Since B is LES, we see the following axioms:
Lexical Axiom: B(n) = k : k ∈ ℕ ∧ k ∉ B(1…n−1).
Earliest Axiom:
If K > k and K also satisfies the other axioms, B(n) = k.
Coprimality Axiom: B(n) = k ⊥ m : m = lcm(B(n−2, n−1)), that is, k belongs to the reduced residue system (RRS) of m.
Theorem B1: Equality is banned in B.
Proof B1: Induction on the lexically earliest axioms. ∎
Theorem B2: 2 | A(3j+1) for j > 0.
Proof B2: The seed terms are odd, therefore u₃ = 2 ⇒ B(4) = 2. Now 2 | m for B(5…6), and none of these terms may be even per coprimality axiom. We introduce odd terms in B, yet u remains even, so whereupon m is no longer even, an even u enters the sequence. Through induction and because numbers are either even or odd, 2 | B(n) : n > 1 ∧ n mod 3 ≡ 1 for n > 1, i.e., 2 | B(3j+1) for j > 0. ∎
Corollary B2.2: There is a smallest missing odd v ∈ ℕ ∧ k ∉ B(1…n−1).
Corollary B2.3: B(3k) and B(3k−1) are odd.
Corollary B2.4: If odd prime q | B(n), then q ⊥ B(n±r) for 1 ≤ r ≤ 2, consequence of axioms.
Theorem B3: Even numbers are not in order.
Proof B3: Let p < q be odd primes. Since we have 2 consecutive odd predecessor terms, Theorem B1 and the coprimality axiom delay 2ps : (p, m) > 1 in favor of 2qs : (q, m) = 1. ∎
Compare this to Theorem A3, where it is plain that even numbers are in order in A.
Theorem B4: Let q be an odd prime. q | B(n) ⇒ q ⊥ B(n±r) : 1 ≤ r ≤ 2, but q may or may not divide B(n±3).
Proof B4: We see q | B(n) ⇒ q ⊥ B(n±r) : 1 ≤ r ≤ 2 for the same reason 2 | B(n) ⇒ 2 ⊥ B(n±r) : 1 ≤ r ≤ 2. However, since we may rewrite q | B(n) as B(n) mod q ≡ 0 and since generally N mod q ∈ {0…q−1}, we have a degree of freedom for q that is not available for 2. Furthermore, since 2 | u and q > 2, if there is an even u : q ⊥ u (or, say u < w : p|u ∧ q|w), though q ⊥ m, on account of lexically earliest axioms, we have k = u instead of q | k. ∎
Compare this to the situation regarding q = 3 vis-à-vis Theorem A3, that harbors odd multiples of 3 in the antipodes between occurrences of even k in A.
Theorem B5: Let q be an odd prime. In a certain interval a ≤ n ≤ b, we either have 2q | B(n) or q | B(n), but not both.
Proof B5: Since 2 | B(3j+i) is confined to i = 1 and since q | B(3j+i) may only again appear for j ≥ 4, we have 2q | B(3j+1) or q | B(3j+i) with i ≠ 1. For q = 3, this is especially relevant, since 6 | B(3j+1) determines the appearance of even or odd numbers divisible by 3 in the sequence. ∎
Corollary B5.1: 6 | B(3j+1) ⇒ 3 ∤ B(3j+i) : 2 ≤ i ≤ 3 and vice versa.
3 | B(3k+j₃) with j₃ moving through all residues mod 3, favoring 1 and 2. We have 6 | B(3k+1) iff 3 | B(3k+1), and this is episodic. When we have 6 | B(3k+1) for certain k, then we cannot have 3 | B(3k+1) odd, and vice versa. When all 6 | u are consumed, then 2 | B(3k+1) indivisible by 3, and 3 | B(3k+j₃) with j₃ ≠ 1. The smallest missing odd number v is generally divisible by 3; once odd m indivisible by 3 appears in the sequence, j₃ moves to 2 (mod 3). The reason why j₃ does not prefer j₃ = 0 is because 3 | v has been exhausted; v is divisible by some larger q, therefore j₃ moves to 1 again so as to admit a number of delayed 6 | u.
Open question B6: What would limit j to freeze such that the sequence B takes in nontrine even numbers or odd trine numbers? Is it always true that the sequence B exhibits cycles wherein 6 | k enter, then odd 3 | k enter? (We say a number is trine iff 3 | k otherwise k is nontrine.)
It is very likely that A352849 is a permutation of ℕ, as Zumkeller “empirically” suggests at A084937.
A352950: Case ℓ = 3.
Let C = A352950, with C(1) = 1, thereafter, C(n) = least k ∈ ℕ ∧ k ∉ C pairwise-coprime to n, C(n−1), C(n−2), and C(n−3).
This is an LES of recursive mappings of function f(m) → k, starting with seed {1} ∪ Prime(2…2+ℓ−1) = {1, 3, 5, 7} : ℓ = 3, where m = lcm(A(n−1…n−ℓ)). The function f is defined below:
f(m) → k : k ∈ ℕ ∧ k ∉ C(1…n−1) ∧ k ⊥ m ∧
(K ∈ ℕ ∧ K ∉ C(1…n−1) ∧ K ⊥ m ∧ K > k.
The sequence begins as follows (See Code 3 and Figure 3):
1, 3, 5, 7, 2, 9, 11, 13, 4, 15, 17, 19, 8, 21, 23, 25, 16, 27, 29, 31, 10, 33, 37, 41, 14, 39, 43, 47, 20, 49, 51, 53, 22, 35, 57, 59, 26, 55, 61, 63, 32, 65, 67, 69, 28, 71, 73, 45, 34, 77, 79, 75, 38, 83, 89, 81, 40, 91, 97, 87, 44, 85, 101, 93, 46, 95, 103, ...
Set the smallest missing number u : u ∈ ℕ ∧ u ∉ C(1…n−1).
Since C is LES, we see the following axioms:
Lexical Axiom: C(n) = k : k ∈ ℕ ∧ k ∉ C(1…n−1).
Earliest Axiom:
If K > k and K also satisfies the other axioms, C(n) = k.
Coprimality Axiom: C(n) = k ⊥ m : m = lcm(C(n−3…n−1)), that is, k belongs to the reduced residue system (RRS) of m.
The following theorems relate to the analogous theorems for A352849.
Theorem C1: Equality is banned in C.
Proof C1: Induction on the lexically earliest axioms.
Theorem C2: 2 | C(n) : n > 1 ∧ n mod 4 ≡ 1.
Proof C2: The seed terms are odd, therefore u₄ = 2 ⇒ C(5) = 2. Now 2|m for C(6…8), and none of these terms may be even per coprimality axiom. We introduce odd terms in C, yet u remains even, so whereupon m is no longer even, an even u enters C. Through induction and because numbers are either even or odd, 2 | C(n) : n > 1 ∧ n mod 4 ≡ 1.
Corollary C2.2: There is a smallest missing odd v ∈ ℕ ∧ k ∉ C(1…n−1).
Corollary C2.3: 2 ∤ C(n–r) : 1 ≤ r ≤ 3 → 2 | C(n) ∧ 2 ∤ C(n+r).
Theorem C3: Let q be an odd prime. q | C(n) ⇒ q ⊥ C(n±r) : 1 ≤ r ≤ 3, but q may or may not divide C(n±4).
Proof C3: We see q | C(n) ⇒ q ⊥ C(n±r) : 1 ≤ r ≤ 3 for the same reason 2 | C(n) ⇒ 2 ⊥ C(n±r) : 1 ≤ r ≤ 3. However, since we may rewrite q | C(n) as C(n) mod q ≡ 0 and since generally N mod q ∈ {0…q−1}, we have a degree of freedom for q that is not available for 2. Furthermore, since 2 | u and q > 2, if there is an even u : q ⊥ u (or, say u < w : p|u ∧ q|w), though q ⊥ m, on account of the lexical axiom we have k = u instead of q | k.
Corollary C3.1: if q | C(n), then q | C(n+4+r), r ≥ 0 via definition of coprime, on the occasion of even m.
Corollary C3.2: all primes p are in C and appear in order outside of p = 2. The exception is a consequence of the seeds being the 3 smallest odd primes.
In sequence C, contrasting the apparent situation in B and certainly in A, we seem to have a problem admitting 6 | k.
We see m₂₂₉ ⊥ 6 → C(229) = u = 6. In fact, C(n) = k = 6s : 229 ≤ n ≤ 337 ∧ n mod 4 ≡ 1. For n < 229, we had seen C(i+j) = 3s migrate from j=2 to 3 at i = 8, and from j=3 to j=0 at i = 10, and from j=0 to j=1 at i = 57, back to j=2 at i = 85. Whereupon we have n = 4(57)+1 = 229, we have m₂₂₉ ⊥ 6 for the first time in C, ushering in u = 6. So long as C(n) = 6s for n = 4i+1, u : 6|u enters C. The regime of C(i+j) = 3s : j = 1 ends at C(341) = 170.
Thereafter we seem to have 2 | C(4i+1) and 3 | C(4i+2). Terms in C divisible by prime q > 3 do not seem to be similarly regulated.
Therefore it seems we have 3 regimes in C:
Regime A includes C(1…228) and has 2 trajectories in A:
A1. Trajectory α is odd, includes C(4i+j) for j ∈ {0, 2, 3}.
A2. Trajectory β is even, includes C(4i+1).
Regime B includes C(229…340) and has 2 trajectories in C:
B1. Trajectory α is odd, includes C(4i+j) for j ∈ {0, 2, 3}.
B2. Trajectory β is divisible by 6, includes C(4i+1).
The regime is fomented by 3|C(n) wandering from n = 4i+j : j≠1 to n = 4i+j : j=1. It ends when once again, 3|A(4i+j) : j≠1 and apparently remaining there.
Regime C includes C(341...) and has 3 trajectories in C:
C1. Trajectory α is odd, includes C(4i+j) for j ∈ {0, 3}.
C2. Trajectory γ is odd and divisible by 3, includes C(4i+2).
C3. Trajectory β is even and indivisible by 3), includes C(4i+1)
In sequence B, these regimes appear to be cyclical (see Figure 2).
Proposition C4: If odd prime q | C(n), then (q, C(n±r)) = 1 for 1 ≤ r ≤ 3, consequence of axioms. This is not to say that q | C(n+4), since there may be a smaller missing number m that satisfies the coprimality axiom.
For this reason, we see 3 | A(4k+j) : j = 2 and n < 8, but j slips such that for n = 229, 2 | C(4k+1) and 3 | C(4k+1) and we may admit numbers divisible by 6 in the sequence. This window is open until C(341) = 170 instead of a number divisible by 6. When C(342) = 351, 3 | C(4k+j) with j = 2 again, and we do not see terms divisible by 6 in the sequence. Thereafter, 2 | C(4k+1) and 3 | C(4k+2).
Primes q > 3 divide C(4k+j) with variable j; their products are not restricted from entry.
Theorem C5: Let q be an odd prime. In a certain interval a ≤ n ≤ b, we either have 2q | C(n) or q | C(n), but not both.
Proof C5: Since 2 | C(4i+j) is confined to j = 1 and since q | C(4i+j) may only again appear for j ≥ 4, we have 2q | C(4i+1) or q | C(4i+j) with j ≠ 1. For q = 3, this is especially relevant, since 6 | C(4i+1) determines the appearance of even or odd numbers divisible by 3 in the sequence.
Open question C6.1: does j take another value for q = 3 and k ≥ 85? If not, then this sequence is not a permutation of natural numbers. If so, then perhaps this sequence has episodes of drawing in terms with the factor 6. In sequence B it seems apparent that the situation is cyclical, whereas in this sequence it is not. Why is that so?
Conjecture C6.2: For n > 341, 3 | C(n) such that n mod 4 = 2.
Observe that for n < 229, C(n) is never divisible by 6. The reason for this is that 2 | C(4i+j) with j = 1 and 3 | C(4i+j) for j ≠ 2. However, m = lcm(A(225…227)) = 2 × 5 × 7 × 11 × 31, denies 315 and 345 from entry in favor of prime C(228)=347. This triggers the admission of 28 consecutive instances of 6 | C(4i+1). 3 primes precede C(341)=170, ending the phase of 6 | C(4i+1). When the sequence was drawing in terms divisible by 6, it had cleared all the even terms divisible by 3 that had not entered the sequence at the expense of detaining odd terms divisible by 3. This created a large reservoir of terms t in A016945 that prove to be the smallest odd numbers not in the sequence. Therefore, we see that for n > 341, we have 2 | C(4i+1) and 3 | C(4i+2). We would require a sustained series of m divisible by several smallest primes q > 3 so as to force a nontrine product P < t to wrest 3 | C(4i+j) from j = 2, but this would only budge it to 3 | C(4i+3). Therefore it is probably an effect of primes p < 4 that p is confined to j, and that the sequence matures at n = 341.
Sequences Sℓ: Cases ℓ > 3.
Suppose we generate sequences Sℓ : ℓ > 3. These are manifestations of Sℓ(1) = 1 followed by Sℓ(n) = prime(n) : 2 ≤ n ≤ ℓ, and for n > ℓ, Sℓ(n) = least k ∈ ℕ ∧ k ∉ Sℓ that is pairwise-coprime to each of Sℓ(n−ℓ…n−1).
Do we see products of all the primes p ≤ ℓ? We are interested in such because of the special relationship 6 = ∏ p : p ≤ ℓ has with Sℓ : ℓ ≤ 3. Certainly, we might see, for example, 2 × 5 or 3 × 5 in Sℓ : ℓ < 5, or 2 × 5 or 3 × 5, 2 × 7, 3 × 7, or 5 × 7 in Sℓ : ℓ < 7. However we expect not to see products of 2, 3, and 5 in Sℓ : ℓ ≥ 5, etc. Code 4 generates charts shown in Figures 4 through 7.
Let's write some general axioms:
General Lexical Axiom: Sℓ(n) = k : k ∈ ℕ ∧ k ∉ Sℓ(1…n−1).
General Earliest Axiom:
If K > k and K also satisfies the other axioms, Sℓ(n) = k.
General Coprimality Axiom: Sℓ(n) = k ⊥ m : m = lcm(Sℓ(n−(ℓ−1), n−1)), that is, k belongs to the reduced residue system (RRS) of m.
We may add that there is a smallest missing number u ∉ Sℓ ∧u ∈ ℕ.
Theorem G1: Equality is banned in Sℓ.
Proof G1: Induction on the lexically earliest axioms. ∎
Theorem G2: 2 | Sℓ((ℓ+1)k + j₂).
Proof G2: Consequence of the lexically earliest and coprimality axioms. Even numbers appear in order as a consequence of the latter axiom and since numbers are either even or odd. Cf. Theorems A1, B2, and C2. ∎
Corollary G2.1: Since 2 divides every other n as n increases, yet appears such that 2 | Sℓ((ℓ+1)k + j₂), u is always even.
Corollary G2.2: There is a smallest missing odd v ∈ ℕ ∧ k ∉ Sℓ(1…n−1).
Corollary G2.3: 2 ∤ Sℓ(n–r) : 1 ≤ r ≤ ℓ → 2 | Sℓ(n) ∧ 2 ∤ Sℓ(n+r).
Theorem G3: Let q be an odd prime. q | Sℓ(n) ⇒ q ⊥ Sℓ(n±r) : 1 ≤ r ≤ ℓ, but q may or may not divide C(n±(ℓ+1)).
Proof G3: We see q | Sℓ(n) ⇒ q ⊥ Sℓ(n±r) : 1 ≤ r ≤ ℓ for the same reason 2 | Sℓ(n) ⇒ 2 ⊥ Sℓ(n±r) : 1 ≤ r ≤ ℓ. However, since we may rewrite q | Sℓ(n) as Sℓ(n) mod q ≡ 0 and since generally N mod q ∈ {0…q−1}, we have a degree of freedom for q that is not available for 2. Furthermore, since 2 | u and q > 2, if there is an even u : q ⊥ u (or, say u < w : p|u ∧ q|w), though q ⊥ m, on account of the lexical axiom we have k = u instead of q | k.
Corollary G3.1: if q | Sℓ(n), then q | Sℓ(n+ℓ+r+1), r ≥ 0 via definition of coprime, on the occasion of even m.
Corollary G3.2: all primes p are in Sℓ and appear in order outside of p = 2. The exception is a consequence of the seeds being the ℓ smallest odd primes.
Proposition G4: Is it true that prime p ≤ ℓ divides Sℓ((ℓ+1)k+jp) for a fixed residue jp (mod (ℓ+1))? This expectation is a generalization of Theorem G2 to primes p ≤ ℓ.
Can we show that we could see further m : 6 | m in A352950 = S₃?
Recap ℓ = 1.
For ℓ = 1, S₁ = A085229 has S₁(2k+1) = 2k : k > 0 and S₁(3k+1) = 3k : k > 1, ∴ S₁(6k+1) = 6k (Theorems A2, A3). The sequence is proved to be a permutation of ℕ. See Figure 1.
Recap ℓ = 2.
For ℓ = 2, S₂ = A352849 has 2 | S₂(3k+1) by Theorem G2. See Figure 2.
3 | S₂(3k+j₃) with j₃ moving through all residues mod (ℓ+1) = 3, favoring 1 and 2. (See Corollary B5.1.) We have 6 | S₂(3k+1) iff 3 | S₂(3k+1), and this is episodic. When we have 6 | S₂(3k+1) for certain k, then we cannot have 3 | S₂(3k+1) odd, and vice versa. When all 6 | u are consumed, then 2 | S₂(3k+1) indivisible by 3, and 3 | S₂(3k+j₃) with j₃ ≠ 1. The smallest missing odd number v is generally divisible by 3; once m ⊥ 6 appears in S₂, j₃ moves to 2 (mod 3). The reason why j₃ does not prefer j₃ = 0 is because 3 | v has been exhausted; v is divisible by some larger q, therefore j₃ moves to 1 again so as to admit a number of delayed 6 | u.
For p > 3, we have p | S₂(3k+jp) for j moving through all residues mod (ℓ+1) = 3, and not for all k.
It is very likely that S₂ is a permutation of ℕ, as Zumkeller “empirically” suggests at A084937.
Recap ℓ = 3.
For ℓ = 3, S₃ = A352950 has 2 | S₃(4k+1) via Theorem G2. See Figure 3.
3 | S₃(4k+j₃) with j₃ beginning at 2 (mod 4). Eventually, we have 3 | S₃(4k+1) for k = 57, i.e., S₃(229) = 6. We see 6 | S₃(4k+1) for 57 ≤ k ≤ 84. Once we have S₃(341) = 170, j₃ moves to 2 (mod 4), where it seems to stay. This seems to be perpetually sustained by 3 | v for n = 4k+2 : n > 341. The fact that 3 odd numbers enter S₃ for each even as n increases seems to undergird the conjecture that this sequence is not a permutation, and that u = 174 remains the smallest missing number as n approaches infinity.
For p > 3, we have p | S₃(4k+jp) for j moving through all residues mod (ℓ+1) = 4, and not for all k.
Case ℓ = 4.
For ℓ = 4, S₄ has 2 | S₄(5k+1) via Theorem G2. See Figure 4.
3 | S₄(5k+j₃) with j₃ = 2 for 0 ≤ k ≤ 18 and j₃ = 3 for k > 18.
5 | S₄(5k+j₅) with j₅ moving through all residues (mod 5) but reluctant to have j₅ = 0 for reasons similar to ℓ = 2 and p = 3.
For p > 5, we have p | S₄(5k+jp) for j moving through all residues mod (ℓ+1) = 5, and not for all k.
In this sequence, it seems m = 6s never appears since j₃ ≠ 1 for all k.
Case ℓ = 5.
For ℓ = 5, S₅ has 2 | S₅(6k+1) via Theorem G2. See Figure 5.
3 | S₅(6k+2), therefore m = 6s never appears. This implies that no odd v : p | v ∧ p > 3 are delayed. Is this so?
5 | S₅(6k+j₅) with j₅ moving through all residues (mod 6), favoring j₅ = 3. S₅(37) = 10, S₅(20) = 15.
For p > 5, we have p | S₅(6k+jp) for j moving through all residues mod (ℓ+1) = 6, and not for all k.
Case ℓ = 6.
For ℓ = 6, S₆ has 2 | S₆(7k+1) via Theorem G2. See Figure 6.
3 | S₆(7k+2), therefore m = 6s never appears. This implies that no odd v : p | v ∧ p > 3 are delayed. Is this so?
5 | S₆(7k+j₅) with j₅ moving through all residues (mod 7), settling on j₅ = 3 for k ≥ 130. S₆(589) = 10, S₆(23) = 15, S₆(737) = 45. Even and trine multiples of 5 have a finite appearance in S₆.
For p > 5, we have p | S₆(7k+jp) for j moving through all residues mod (ℓ+1) = 7, and not for all k.
Case ℓ = 7.
For ℓ = 7, S₇ has 2 | S₇(8k+1) via Theorem G2. See Figure 7.
3 | S₇(8k+2), therefore m = 6s never appears. This implies that no odd v : p | v ∧ p > 3 are delayed. Is this so?
5 | S₇(8k+j₅) with j₅ moving through {3, 4, 6} (mod 8), settling on j₅ = 7 for k ≥ 5. Consequently, multiples of any combination of at least two of the primes {2, 3, 5} do not appear in S₇.
7 | S₇(8k+j₇) with j₇ moving through all residues (mod 8), largely avoiding {4, 5, 6} and preferring j₇ = 3. S₇(113) = 14, S₇(18) = 21, S₇(121) = 28, S₇(38) = 35, etc. Does j₇ settle on a residue (mod 8)? If so, then further multiples of smaller primes and 7 may not enter unless j₇ = jp for prime p < 7.
For p > 7, we have p | S₇(8k+jp) for j moving through all residues mod (ℓ+1) = 8, and not for all k.
Case ℓ = 8.
For ℓ = 8, S₈ has 2 | S₈(9k+1) via Theorem G2.
3 | S₈(9k+2), therefore m = 6s never appears. This implies that no odd v : p | v ∧ p > 3 are delayed. Is this so?
5 | S₈(9k+j₅) with j₅ slipping from 3 to 4 (mod 9), settling on j₅ = 5 for k ≥ 15. Consequently, multiples of any combination of at least two of the primes {2, 3, 5} do not appear in S₈.
7 | S₈(9k+j₇) with j₇ moving through all residues (mod 9) but 0, preferring j₇ = 3 and to a lesser degree 6 and 5. S₈(55) = 14, S₈(20) = 21, S₈(595) = 28, S₈(40) = 35, etc. Does j₇ settle on a residue (mod 9)? If so, then further multiples of smaller primes and 7 may not enter unless j₇ = jp for prime p < 7.
For p > 7, we have p | S₈(9k+jp) for j moving through all residues mod (ℓ+1) = 9, and not for all k.
Case ℓ = 9.
For ℓ = 9, S₉ has 2 | S₉(10k+1) via Theorem G2.
3 | S₉(10k+2), therefore m = 6s never appears. This implies that no odd v : p | v ∧ p > 3 are delayed. Is this so?
5 | S₉(10k+j₅) with j₅ slipping from 3 to settle on j₅ = 4 for k ≥ 5. Consequently, multiples of any combination of at least two of the primes {2, 3, 5} do not appear in S₉.
7 | S₉(10k+j₇) with j₇ taking {4, 9, 2} (mod 10) for k ≤ 3, then j₇ = 3 for 4 ≤ k ≤ 110, then j₇ = 4 for 111 ≤ k ≤ 127. For k > 127, j₇ = 5. Therefore we have S₉(32) = 21, but no other products of prime p < 7 and 7 in S₉.
For p > 7, we have p | S₉(10k+jp) for j moving through all residues mod (ℓ+1) = 10, and not for all k.
Case ℓ = 10.
For ℓ = 10, S₁₀ has 2 | S₁₀(11k+1) via Theorem G2.
3 | S₁₀(11k+2), therefore m = 6s never appears. This implies that no odd v : p | v ∧ p > 3 are delayed. Is this so?
5 | S₁₀(11k+j₅) with j₅ slipping from 3 to settle on j₅ = 4 for k ≥ 7. Consequently, multiples of any combination of at least two of the primes {2, 3, 5} do not appear in S₁₀.
7 | S₁₀(11k+j₇) with j₇ taking {4, 8, 10, 1, 2} (mod 11) for k ≤ 5, j₇ = 3 for 6 ≤ k ≤ 10, j₇ = 4 for k = 11. For k > 11, j₇ = 5. Therefore we have S₁₀(45) = 14, S₁₀(57) = 21, and S₁₀(69) = 35, but j₅ ≠ j₇ for k > 6. Thus, no other products of prime p < 7 and 7 in S₁₀.
For p > 7, we have p | S₁₀(11k+jp) for j moving through all residues mod (ℓ+1) = 11, and not for all k.
Case ℓ = 11.
For ℓ = 11, S₁₁ has 2 | S₁₁(12k+1) via Theorem G2.
3 | S₁₁(12k+2), therefore m = 6s never appears. This implies that no odd v : p | v ∧ p > 3 are delayed. Is this so?
5 | S₁₁(12k+3), consequently, multiples of any combination of at least two of the primes {2, 3, 5} do not appear in S₁₁.
7 | S₁₁(12k+j₇) with j₇ taking {4, 7, 8, 1, 2, 3} (mod 12) for k ≤ 6. For k > 6, j₇ = 4. Therefore we have S₁₁(49) = 14, S₁₁(62) = 21, and S₁₁(75) = 35. No other products of prime p < 7 and 7 in S₁₀.
11 | S₁₁(12k+j₁₁) with j₁₁ taking nonzero residues (mod 12) but preferring 5. Does j₁₁ = 0 occur?
For p > 11, we have p | S₁₁(12k+jp) for j moving through all residues mod (ℓ+1) = 12, and not for all k.
Case ℓ = 12.
For ℓ = 12, S₁₂ has 2 | S₁₂(13k+1) via Theorem G2.
3 | S₁₂(13k+2), therefore m = 6s never appears. This implies that no odd v : p | v ∧ p > 3 are delayed. Is this so?
5 | S₁₂(13k+3), with j₅ slipping from 3 to settle on j₅ = 4 for k ≥ 11.
7 | S₁₂(13k+j₇) with j₇ taking {4, 6, 6} (mod 13) for k ≤ 3. j₇ = 11 for 4 ≤ k ≤ 7. For k > 7, j₇ = 12. Consequently, multiples of any combination of at least two of the primes {2, 3, 5, 7} do not appear in S₁₂.
11 | S₁₁(13k+j₁₁) with j₁₁ shifting through residues (mod 13).
For p > 11, we have p | S₁₁(13k+jp) for j moving through all residues mod (ℓ+1) = 12, and not for all k.
Therefore, we have shown that Proposition G4 is false, i.e., that prime p ≤ ℓ divides Sℓ((ℓ+1)k+jp) for a fixed residue jp (mod (ℓ+1)). The counterexample regards p = 5 for ℓ > 5, except ℓ = 11. We should also expect p = 7 to settle on a residue for ℓ > 7, and have not seen such settling for ℓ ≤ 12.
The question of slippage of j₃ in S₃ =A352950 from 2 eventually to realign with j₂ = 1 so as to admit further multiples of 6 in S₃ (and similar considerations) remains open. The case of j₃ = 2 for k > 84 in S₃ = A352950 is tantamount to 3 | v at n = 4k + 2 : k > 84. This seems to be closed to any movement of j₃, meaning that indeed, all smallest unused odd numbers are divisible by 3 for n > 341.
Conclusion.
The lexically earliest axioms and mandatory coprimality of current term k with ℓ previous terms yields similar theorems across sequences Sℓ. It is easy to see that Sℓ((ℓ+1)i+1) = 2(i+1) for ℓ=1. For ℓ=1, 3 | Sℓ(3i+1) for i > 0, but for ℓ=2, we may either have 6 | k or 3 | k. Generally, Sℓ((ℓ+1)k + j₂) and the smallest missing number u are even. We acknowledge a smallest missing odd number v ∈ ℕ ∧ k ∉ Sℓ(1…n−1). Prime q | Sℓ(n) implies q coprime to Sℓ(n±r) : 1 ≤ r ≤ ℓ and q | Sℓ(n+ℓ+r+1), r ≥ 0. All primes p are in Sℓ and appear in order outside of p = 2. We showed counterexamples to the proposition (G4) that prime p ≤ ℓ divides Sℓ((ℓ+1)k+jp) for a fixed residue jp (mod (ℓ+1)).
Some open questions:
Do we see multiples of 6 greater than 168 in A352950? It doesn’t seem likely. Is the same true for multiples of 10 in case ℓ = 4? Is it true that intervals of 6 | m alternate with 3 | m odd in A352849 ad infinitum? Are primes p = prime(j), 1 ≤ j ≤ 3 confined to j (mod 12) in case ℓ = 11? What is the reason why Proposition G4 fails, and why does it seem to hold in the case of p = 5 and ℓ = 11? Why is it that it seems prime(j) | Sℓ((ℓ+1)k+j) for j = 2 and ℓ > 4? If it really is that 3 < ℓ, then why is something similar not true for prime(j) > 3?
This concludes our examination.
Appendix.
Figure 1: Log-log scatterplot of A(n), n = 1..2⁸, highlighting prime A(n) in green, 6 | A(n) in amber. Nontrine even numbers are shown in red and odd trine numbers in blue.
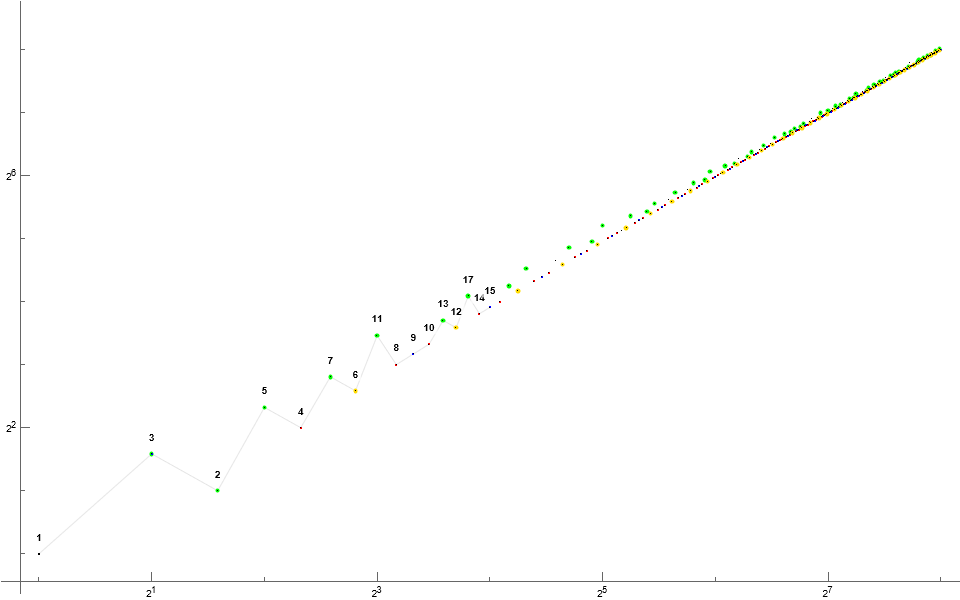
Figure 2: Log-log scatterplot of B(n), n = 1..2¹², highlighting prime B(n) in green, 6 | B(n) in amber. Nontrine even numbers are shown in red and odd trine numbers in blue.
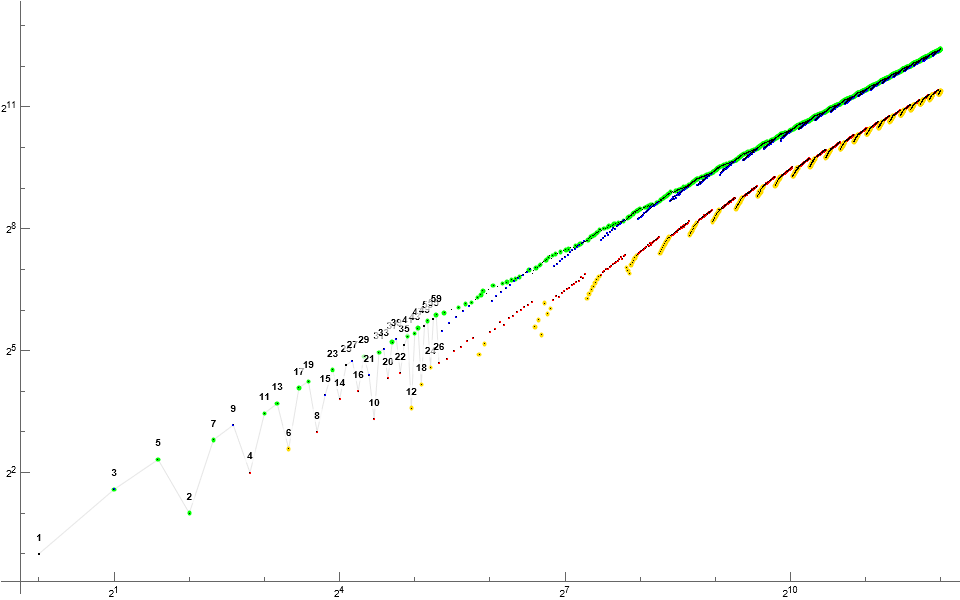
Figure 3: Log-log scatterplot of C(n), n = 1..2¹⁰, highlighting prime C(n) in green, 6 | C(n) in amber. Nontrine even numbers are shown in red and odd trine numbers in blue.
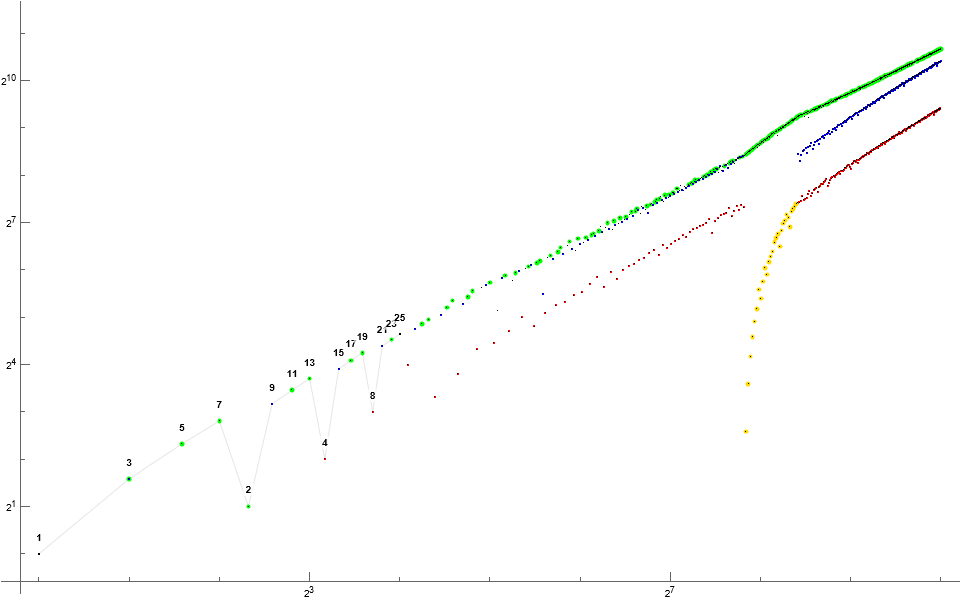
Figure 4: Log-log scatterplot of Sℓ(n) : ℓ = 4 ∧ n = 1..2¹⁰, highlighting prime m = S₄(n) in green, 6 | m in amber. Nontrine even numbers m are shown in red and odd trine numbers m in blue. We note that there appear to be no m divisible by 6 in the sequence, and that we also find that even multiples of 5 enter late. The first number not divisible by 6 missing from the sequence is 590.
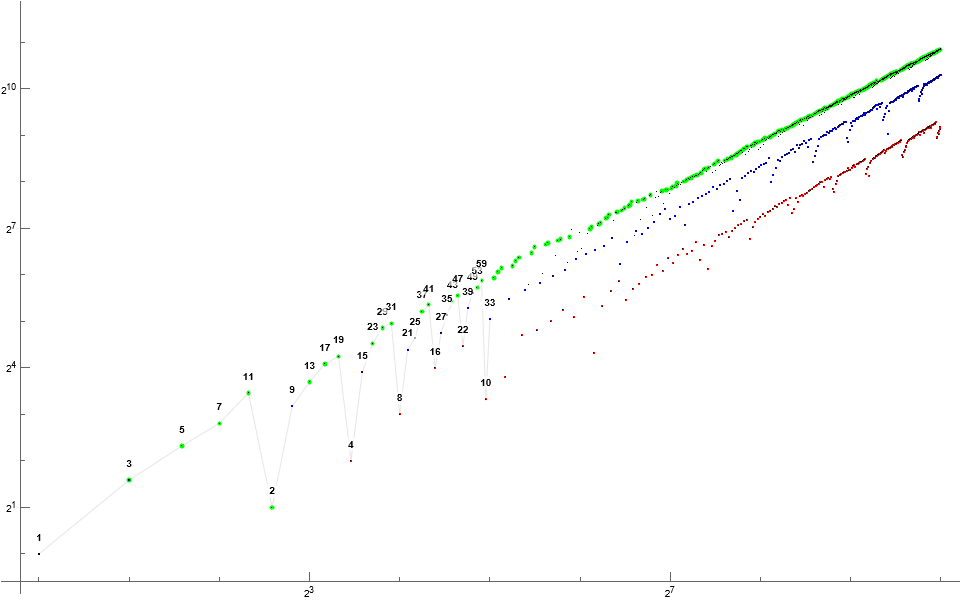
Figure 5: Log-log scatterplot of Sℓ(n) : ℓ = 5 ∧ n = 1..2¹⁰, highlighting prime m = S₅(n) in green, 6 | m in amber. Nontrine even numbers m are shown in red and odd trine numbers m in blue. We note that there appear to be no m divisible by 6 in the sequence, and that we also find that even multiples of 5 enter late. The low-hanging terms at right are multiples of 5.
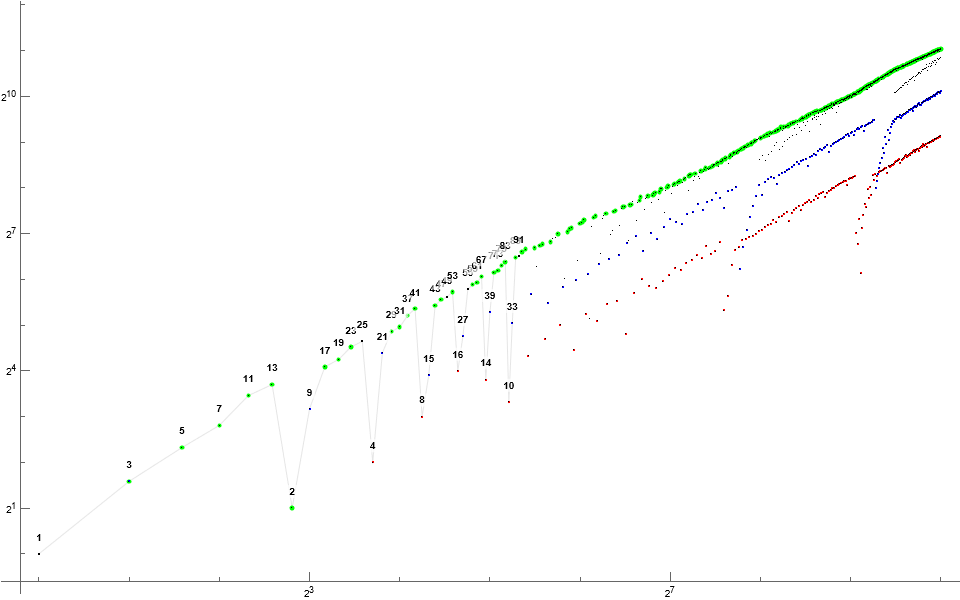
Figure 6: Log-log scatterplot of Sℓ(n) : ℓ = 6 ∧ n = 1..2¹⁰, highlighting prime m = S₆(n) in green, 6 | m in amber. Nontrine even numbers m are shown in red and odd trine numbers m in blue. We note that there appear to be no m divisible by 6 in the sequence, and that we also find that even multiples of 5 enter late. The lowest-hanging even term at right is m = 14.
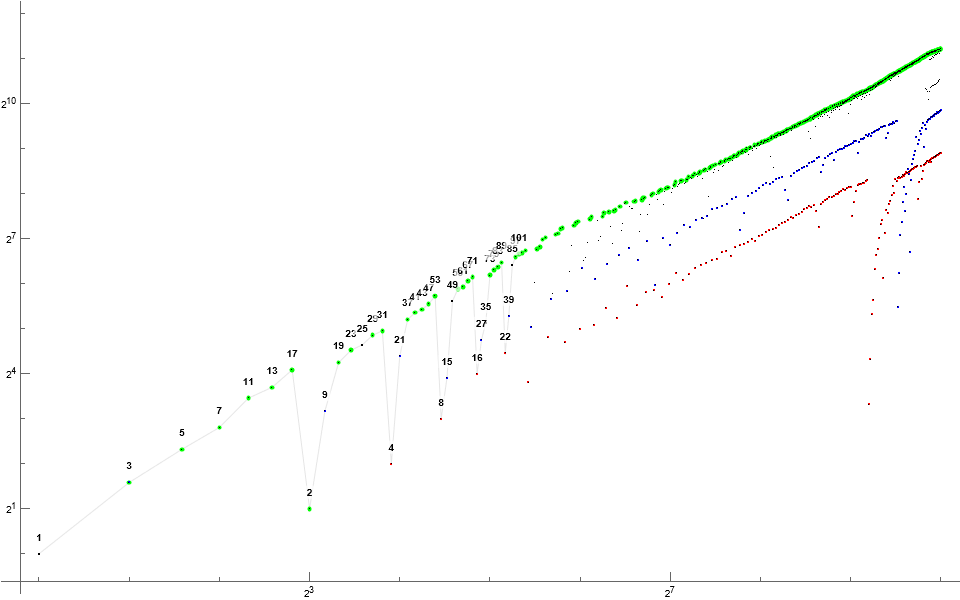
Figure 7: Log-log scatterplot of Sℓ(n) : ℓ = 7 ∧ n = 1..2¹⁰, highlighting prime m = S₇(n) in green, 6 | m in amber. Nontrine even numbers m are shown in red and odd trine numbers m in blue. We note that there appear to be no m divisible by 6 or 10 in the sequence, and that we also find that even multiples of 7 enter late. The lowest-hanging even term at right is m = 14.
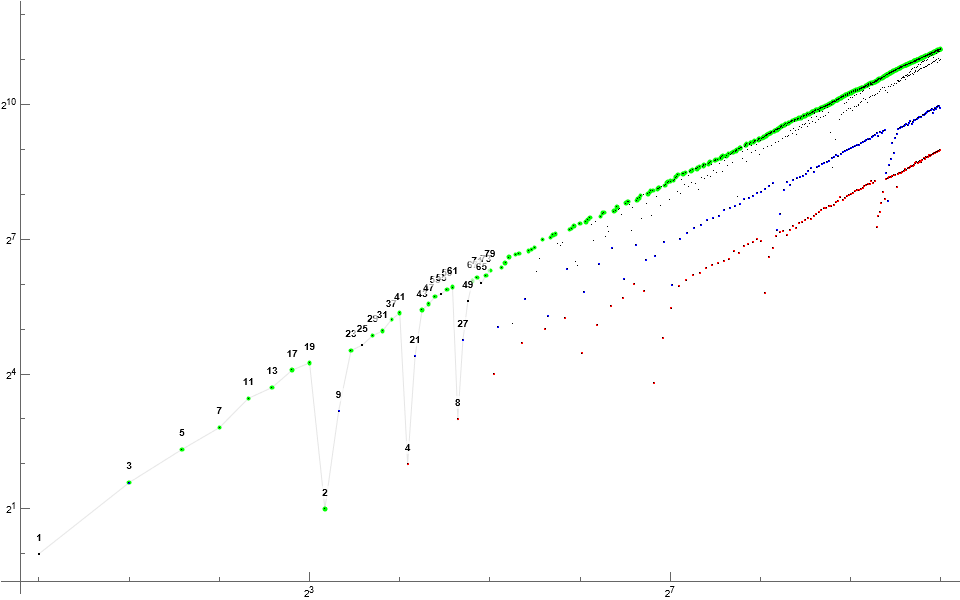
References:
Code 1: Generate over a million terms of A in about a minute:
a085229 = Block[{nn = 2^20, ll = 1, a, c, k, m, u = 1},
c[_] = 0;
MapIndexed[Set[{a[First[#2]], c[#1]}, {#1, First[#2]}] &,
{1}~Join~Prime[Range[2, 1 + ll]]]; While[c[u] > 0, u++];
Monitor[Do[k = u; m = LCM @@ Array[a[i - #] &, ll];
While[Nand[c[k] == 0, CoprimeQ[m, k]], k++];
Set[{a[i], c[k]}, {k, i}];
If[a[i] == u, While[c[u] > 0, u++]], {i, ll + 2, nn}], i];
Array[a, nn]];
a352849 = Block[{nn = 2^12, a, c, k, m, u = 1},
c[_] = 0;
MapIndexed[Set[{a[First[#2]], c[#1]}, {#1, First[#2]}] &, {1, 3, 5}];
While[c[u] > 0, u++];
Monitor[Do[k = u; m = LCM @@ Array[a[i - #] &, 2];
While[Nand[c[k] == 0, CoprimeQ[m, k]], k++];
Set[{a[i], c[k]}, {k, i}];
If[a[i] == u, While[c[u] > 0, u++]], {i, 4, nn}], i];
Array[a, nn]]
a352950 = Block[{nn = 2^12, a, c, k, m, u = 1},
c[_] = 0;
MapIndexed[Set[{a[First[#2]], c[#1]}, {#1, First[#2]}] &, {1, 3, 5, 7}];
While[c[u] > 0, u++];
Monitor[Do[k = u; m = LCM @@ Array[a[i - #] &, 3];
While[Nand[c[k] == 0, CoprimeQ[m, k]], k++];
Set[{a[i], c[k]}, {k, i}];
If[a[i] == u, While[c[u] > 0, u++]], {i, 5, nn}], i]; Array[a, nn]]
Code 4: Generate Sℓ by setting ℓ = ll and nn = number of terms desired:
Block[{nn = 2^10, kk = 2^5, a, c, k, ll = 7, m, p, r, s, t, u = 1, Gold = Hue[1/7]},
MapIndexed[Set[{a[First[#2]], c[#1]}, {#1, First[#2]}] &, {1}~Join~Prime[Range[2, 1 + ll]]];
While[c[u] > 0, u++];
Monitor[Do[k = u; m = LCM @@ Array[a[i - #] &, ll];
While[Nand[c[k] == 0, CoprimeQ[m, k]], k++];
Set[{a[i], c[k]}, {k, i}];
If[a[i] == u, While[c[u] > 0, u++]], {i, ll + 2, nn}], i];
a = Array[a, nn];
r = Array[If[Mod[#, 6] == 0, #] &@a[[#]] &, nn];
s = Array[If[Mod[#, 3] == 0, #] &@a[[#]] &, nn];
t = Array[If[Mod[#, 2] == 0, #] &@a[[#]] &, nn];
p = Array[If[PrimeQ[#], #] &@a[[#]] &, nn];
ListPlot[{a[[1 ;; kk]], a[[1 ;; kk]], t, p, s, r, a,
Array[Labeled[#, #, Top, LabelStyle -> {Bold, Black}] &@a[[#]] &, kk]},
ImageSize -> 960, Joined -> {True}~Join~ConstantArray[False, 7],
ScalingFunctions -> {"Log2", "Log2"},
PlotStyle -> {
Directive[Gray, Thin],
Directive[Black, PointSize[Small]],
Directive[Red, PointSize[Small]],
Directive[Green, PointSize[Medium]],
Directive[Blue, PointSize[Small]],
Directive[Gold, PointSize[Medium]],
Directive[Black, PointSize[Tiny]],
Transparent, Transparent, Transparent}] ]
Concerns sequences:
A084937: S(1)=1, S(2)=2; S(n) = least k ∈ ℕ ∧ k ∉ S pairwise-coprime S(n−1) and S(n−2).
A085229: S(1)=1; S(n) = least k ∈ ℕ ∧ k ∉ S pairwise-coprime to n and S(n−1).
A352849: S(1)=1, S(2)=3, S(3)=5; S(n) = least k ∈ ℕ ∧ k ∉ S pairwise-coprime to S(n−1) and S(n−2).
A352950: S(1)=1, S(2)=3, S(3)=5, S(4)=7; S(n) = least k ∈ ℕ ∧ k ∉ S pairwise-coprime S(n−1), S(n−2), and S(n−3).
Document Revision Record.
2022 0424 0930 Draft.
2022 0426 1300 Study of 4 ≤ ℓ ≤ 12.
2022 0426 1530 Final.