Recursive prime counting function sequences.
OEIS A114897, a sequence of Leroy Quet.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0930.
Introduction.
Let a(1) = 1. a(n+1) = card(a(k)), 1 ≤ k ≤ n, such that a(k) + n is prime, where card(m) = c(m) is the number of qualified m in the multiset.
The sequence a begins:
1, 1, 2, 1, 3, 1, 4, 1, 1, 2, 7, 2, 7, 1, 1, 4, 11, 3, 9, 2, 4, 4, 11, 0, 2, 4, 4, 11, 11, 6, 14, 2, 5, 7, 6, 8, 16, 10, 4, 15, 13, 9, 13, 10, 5, 9, 14, 5, 9, 9, 11, 10, 17, 6, 9, 11, 13, 19, 20, 11, 22, 8, 17, 14, 13, 14, 20, 13, 13, 22, 23, 9, 20, 8, 12, 16, 11, 13, 21, 13, 13, 16, 14, 12, 16, 15, 16, 24, 28, 15, 24, 15, 25, 26, 26, 19, 33, 21, 25, 25, 29, 17, 26, 17, 14, 21, 20, 16, 15, 11, 10, 20, 18, 13, 18, 12, 19, 17, 24, 13, 21, ...
a(2) = 1 since n + a(1) = 1 + 1 = 2 is prime.
a(3) = 2 since n + a(1..2) = 2 + {1,1} = {2,2}, both are prime.
a(4) = 1 since 3 + {1,1,2} = {4,4,5}, only 1 is prime.
a(5) = 3 since 4 + {1,1,2,1} = {5,5,6,5}, and there are 3 primes in the list, etc.
We find computationally, recognizing a(n) << n as n increases, that though we might add n to each m in a(1..n) so as to count primes, we might circumvent such by means of registers c(m) and set Dn of distinct m in a(1..n); if we find n + m prime, then we sum all the qualified c(m) and arrive at a(n+1). Therefore we might rewrite the definition as:
a(1) = 1; a(n+1) = Sum_{m ∈Dn, m + n prime} c(m).
This sequence can be generated efficiently by Code 1, which is faster than the Mathematica code that appears at OEIS A114897. We have generated 219 terms that we call herein the “dataset”.
Figure 1 is a labeled scatterplot of a(n) for 1 ≤ n ≤ 128. Records r appear in red and probable local minima s in blue. Terms highlighted in green represent the first appearance of the least gap u in a.
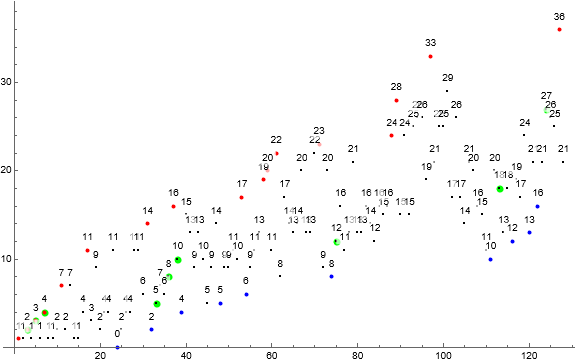
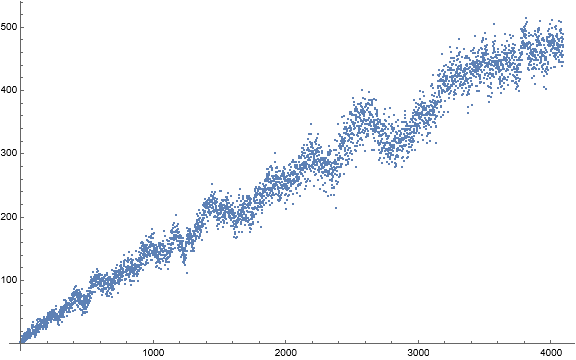
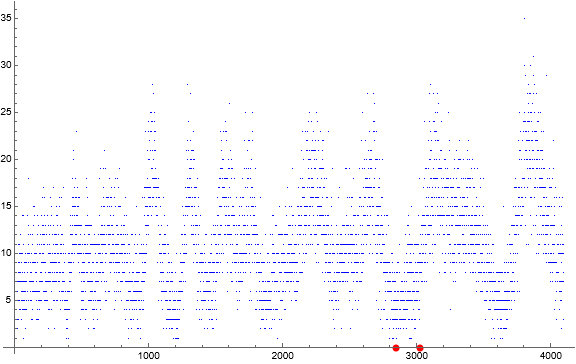
Figure 2 is a scatterplot of a(n) for 1 ≤ n ≤ 4096. Click here for a large scatterplot of a(n) for 1 ≤ n ≤ 524288.
Records r are easy to find:
1, 2, 3, 4, 7, 11, 14, 16, 17, 19, 20, 22, 23, 24, 28, 33, 36, 38, 42, 44, 47, 48, 49, 50, 52, 53, 54, 59, 68, 69, 71, 72, 76, 78, 79, 85, 89, 90, 96, 100, 104, 113, 118, 119, 123, 124, 129, 130, 140, 144, 145, 150, 151, 159, 160, 170, 173, 180, 187, 190, ...
Their indices i are:
1, 3, 5, 7, 11, 17, 31, 37, 53, 58, 59, 61, 71, 88, 89, 97, 127, 139, 178, 208, 214, 226, 227, 238, 244, 256, 268, 269, 334, 337, 373, 382, 389, 394, 401, 406, 418, 419, 530, 536, 538, 554, 584, 724, 731, 760, 761, 782, 785, 820, 878, 908, 911, 914, 920, 950, 992, 998, 1151, 1160, ...
Through reversal of the dataset we arrive at a sequence s of probable local minima:
0, 2, 4, 5, 6, 8, 10, 12, 13, 16, 18, 22, 23, 25, 28, 34, 42, 43, 45, 47, 48, 49, 60, 64, 66, 71, 73, 79, 92, 98, 111, 145, 151, 161, 163, 166, 168, 176, 180, 183, 205, 212, 214, 252, 254, 262, 264, 267, 278, 279, 288, 292, 295, 301, 302, 306, 316, 357, 358, 360, ...
These are found at a(j) for j in:
24, 32, 39, 48, 54, 74, 111, 116, 120, 122, 140, 175, 195, 201, 291, 315, 333, 357, 465, 477, 490, 507, 512, 517, 525, 537, 693, 742, 837, 889, 1257, 1309, 1312, 1318, 1369, 1626, 1637, 1737, 1744, 1816, 1826, 2008, 2380, 2392, 2396, 2406, 2416, 2446, 2828, 2884, 2896, 2916, 2926, 2928, 2937, 2979, 3136, 3138, 3172, 3189, ...
We would like to ascertain a lower bound for a such that we might validate local minima. Consider the function w(n) = π(r + n) − π(n) − [¬ isprime(n)], where r is the latest record in a(1..n) and brackets are Iverson. This function increases and decreases, therefore doesn’t serve as a proper lower bound, but it does render an idea of the number of distinct primes we could have between n and (r + n) inclusive, and we expect such a figure to be high. A better function measured during generation would be to count the number q(p) of primes p = (n+m) in n + Dn. There seems to be little error between the functions w and q, with the former the larger. We find that due to the multiplicity of m represented by c(m), the actual a(n) is much larger than w(n) or q(n) as n increases beyond a few dozen terms.
Sequence w begins as follows:
0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 2, 2, 2, 3, 2, 3, 2, 3, 3, 3, 2, 2, 2, 3, 3, 3, 2, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 3, 3, 4, 4, 3, 3, 3, 3, 4, 4, 3, 4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 4, 4, 3, 4, 4, 4, 4, 5, 4, 5, 5, 5, 4, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 6, 6, 5, 6, 6, 7, 6, 6, 5, 5, 5, 5, 4, 4, 4, 5, 5, 6, 6, 6, ...
Sequence q begins as follows:
0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 2, 1, 1, 2, 3, 1, 2, 1, 3, 1, 3, 0, 1, 1, 2, 2, 3, 2, 3, 2, 2, 2, 3, 2, 4, 4, 3, 4, 3, 3, 3, 4, 3, 4, 4, 3, 3, 2, 3, 4, 4, 4, 4, 3, 5, 5, 5, 5, 5, 4, 4, 5, 5, 4, 5, 5, 4, 5, 5, 3, 4, 4, 4, 4, 3, 4, 5, 4, 5, 5, 5, 4, 5, 4, 6, 6, 6, 6, 6, 5, 6, 6, 6, 5, 6, 6, 6, 6, 5, 6, 6, 6, 5, 5, 6, 5, 5, 4, 4, 5, 4, 5, 4, 4, 5, 4, 5, 4, 5, ...
Figure 3 is a scatterplot of a(n) for 1 ≤ n ≤ 256 using the same color scheme as Figure 1, but adding w(n) in gold and q(n) in magenta.
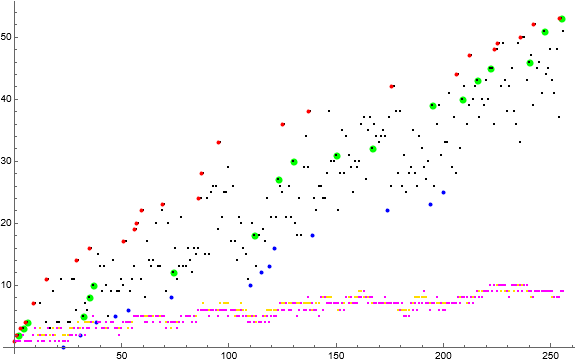
We consider the function u(n), which notes the least m not found in a(1..n).
0, 8, 10, 12, 18, 27, 30, 31, 32, 39, 40, 43, 45, 46, 51, 53, 54, 55, 56, 60, 62, 63, 65, 66, 77, 80, 83, 87, 88, 91, 94, 98, 109, 116, 125, 135, 136, 137, 143, 153, 158, 162, 164, 175, 181, 184, 193, 195, 196, 235, 242, 246, 248, 254, 273, 283, 285, 288, 294, 374, 376, 381, 389, 392, 402, 471, 474, 475, 481, 491, 502, 503, 505, 512, 518, 527, 532, 533, 544, 545, 547, 553, 567, 573, 580, 585, 590, 602, 617, 624, 633, 672, 673, 679, 684, 685, 717, 734, 736, 747, 756, 761, 780, 786, 793, 794, 803, 819, 822, 869, 873, 883, 897, 905, 916, 930, 934, 954, 1003, 1009, 1015, 1016, 1024, 1026, 1027, 1038, 1054, 1057, 1059, 1077, 1081, 1090, 1094, 1101, 1102, 1111, 1115, 1143, 1158, 1164, 1167, 1182, 1188, 1207, 1213, 1334, 1337, 1357, 1378, 1394, 1409, 1418, 1430, 1439, 1447, 1468, 1469, 1475, 1480, 1488, 1501, 1503, 1557, 1607, 1631, 1652, 1678, 1685, 1690, 1703, 1711, 1720, 1721, 1752, 1778, 1830, 1832, 1845, 1850, 1862, 1872, 1886, 1920, 1960, 2113, 2132, 2148, 2152, 2155, 2171, 2178, 2231, 2232, 2244, 2275, 2277, 2280, 2332, 2350, 2356, 2361, 2385, 2386, 2394, 2406, 2413, 2496, 2509, 2565, 2584, 2605, 2699, 2701, 2725, 2745, 2795, 2796, 2830, 2844
Though a(1) = 1 and we see 8 copies of 1 overall within the first 15 terms of the sequence, 0 does not appear until a(24), and there seems to be only one in the sequence.
At the start of the function there are often multiple copies of m in a(1..n), however it is not guaranteed that a covers the nonnegative integers. There appears to be a sort of lower bound to the function such that there is a finite number c(m) of terms m in a.
If there is indeed a lower bound, then we find that 2844, 3020, and 13595 are missing from a, given the dataset whose maximum m = 40228 and number of distinct terms is 39942, hence, finding the first gap in a has little value.
Given the dataset, we may tabulate the number m, the cardinality c(m) of m in a, and the first and last index i and j, respectively, of m in a.
Table 1.
m c(m) i j
-----------------
0 1 24 24
1 8 1 15
2 6 3 32
3 2 5 18
4 7 7 39
5 3 33 48
6 3 30 54
7 3 11 34
8 3 36 74
9 7 19 72
10 4 38 111
11 9 17 110
12 3 75 116
...
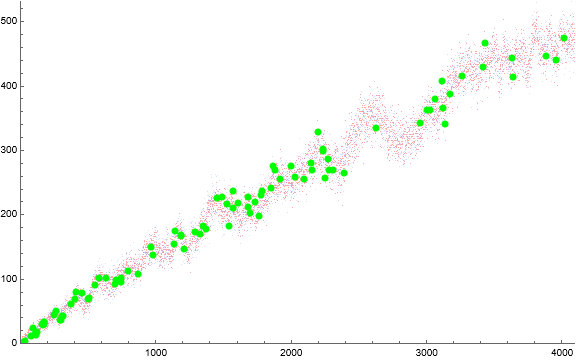
We see that c(2844) = 0, and i and j are undefined for m = 2844. Assuming there is a lower limit, we might plot the first indices and cardinalities of m, i.e., i(m) and c(m), respectively. These are portrayed in Figures 3 and 4 respectively, considering the size of the dataset that exhibited further “missing” terms around m = 30000.
Figure 4 is a scatterplot of i(m) for 1 ≤ m ≤ 4096, accentuating i(2844) = i(3020) = 0 in red, which we define as representing absence from a.
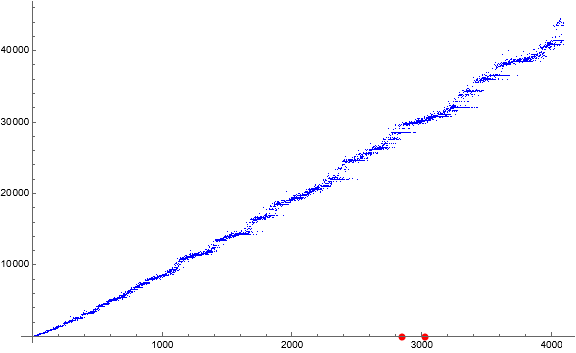
Figure 5 is a scatterplot of c(m) for 1 ≤ m ≤ 4096, accentuating c(2844) = c(3020) = 0.
OEIS A114897 is identical to A123541 if the first 3 terms of each (as presented, ignoring offsets) are eliminated. At least 2 other sequences appear to apply the same algorithm to different seeds or with different offsets. We have A108839 which features n incremented from that of A114897. The first missing m in that sequence is 1203.
Figure 6 is a labeled scatterplot of A108839(n) for 1 ≤ n ≤ 128, compare to Figure 1. Records r appear in red and probable local minima s in blue. Terms highlighted in green represent the first appearance of the least gap u in a.
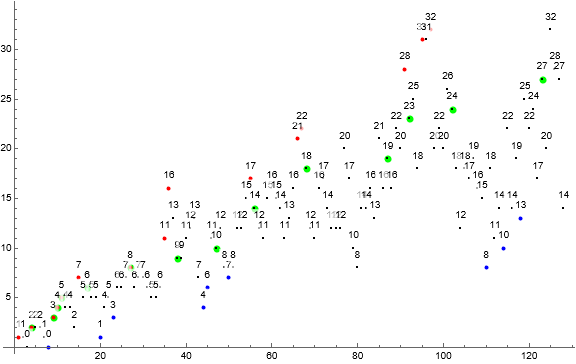
Figure 7 is a scatterplot of A108839(n) for 1 ≤ n ≤ 256 using the same color scheme as Figure 6, but adding w(n) in gold and q(n) in magenta. Compare with Figure 3 that pertains to A114897.
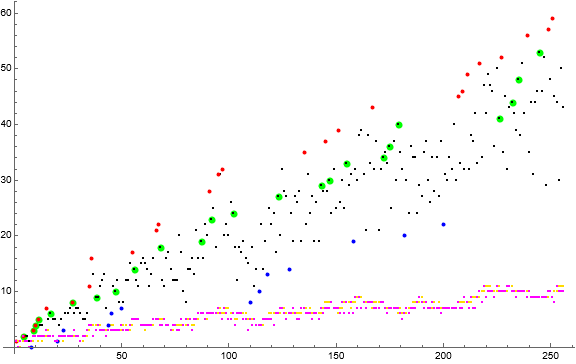
Figure 8 overlays the scatterplot of A114897(n) in pink with A108839(n) in light blue, 1 ≤ n ≤ 212; occasions where A114897(n) = A108839(n) are shown in green.
It is our observation that A108839, A114897-9, and A123541 share common traits. Is there a way to find a lower limit such that we can ascertain local minima?
We can demonstrate by construction that A108839, A114897, and A123541 do not cover the nonnegative integers, provided we can find a good lower bound.
This concludes our examination.
Appendix:
Block[{c, r = {1}, k},
c[1] = 1;
{1}~Join~Reap[
Do[Set[k, Total@ Map[c[#] &, Select[r, PrimeQ[# + i] &]]];
If[IntegerQ[c[k]], c[k]++, Set[c[k], 1]; AppendTo[r, k];
Sow[k], {i, 2^10}]
][[-1, 1]] ]
Concerns OEIS sequences:
A090405: a(n) = π(n + 2) − π(n).
A108839: a(1) = 1. a(n+1) = card(a(k)), 1 ≤ k ≤ n+1, such that a(k) + n is prime
A114897: a(1) = 1. a(n+1) = card(a(k)), 1 ≤ k ≤ n, such that a(k) + n is prime.
A123541: a(0) = 2; for n > 0, a(n) = number of earlier terms which when added to n give a prime.
Document Revision Record.
2021 0930 2045: Final.