OEIS A137417
A sequence by Ctibor O. Zizka, 2008 0416
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0804
Some variants explored attribute to David J. Sycamore of Mevagissey, England, UK .
Introduction.
Let the sequence s = OEIS A137417 be a “limiting sequence” (in the parlance of Zizka) that begins as the sequence A27 of positive integers s(n) = n for all n ≥ 1. We iterate a function f(i): s(i) + s( j) → s( j) at step i with j = i + s(i), thereby possibly altering the term s(n) one or more times. Because s(n) is in positive integers, step i casts change at s( j) for j > i, hence we may take the terms s(1..i) as “crystallized” or immutable by subsequent steps. As a consequence, step i imparts change at s( j) for some j ≫ i as i increases.
The sequence s(n) begins:
1, 3, 3, 4, 8, 9, 7, 12, 9, 10, 11, 12, 21, 21, 24, 16, 17, 27, 19, 42, 21, 33, 23, 36, 25, 26, 27, 28, 29, 30, 31, 48, 33, 72, 56, 36, 37, 57, 63, 40, 41, 63, 43, 44, 72, 69, 47, 48, 49, 75, 51, 78, 53, 81, 88, 84, 57, 87, 59, 126, 61, 135, 63, 64, 65, 99, ...
Code 1 generates 224 = 16777216 terms in less than 90 s.
Figure 1.1 is a scatterplot of s(n) for 1 ≤ n ≤ 26. Terms s(n) = n appear in black. Terms annotated in blue have been changed once, and in orange twice.
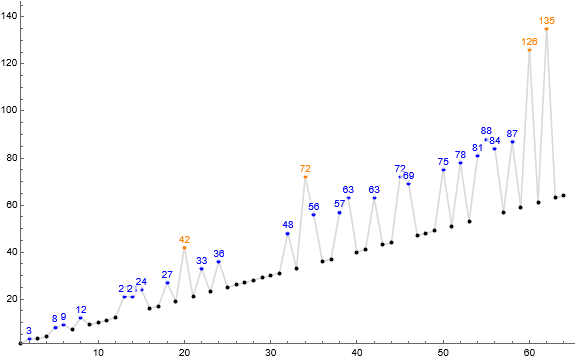
Figure 1.2 is a scatterplot of s(n) for 1 ≤ n ≤ 218. Terms s(n) = n are plotted in black. Terms that have been changed once appear in blue, twice in gold, and three times in red. The streams of terms that have been altered at least once loosely register the configuration of the scatterplot on account of the function f(i).
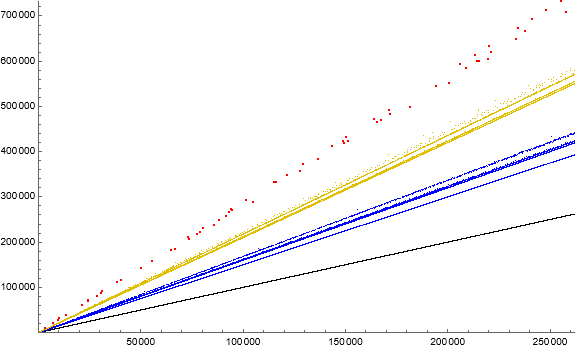
There are several features of this sequence that merit exploration. These include the number of edits c( j) imposed on term s( j), the behavior of a sidecar sequence j(i) = i + s(i) as i increases, and the cardinality k(m) of terms m in s. We might also consider the trajectory of a given term s(n) as i increases such that no edit can occur on s(n).
Editing s( j).
Step 1 has s(1) + s(j) → s(j) where s(j) = s(1 + s(1)) = s(1+1) = s(2). Therefore we change s(2) = 2 to s(2) = 2+1 = 3. Furthermore, s(1) is assured not to change: we can say that s(1) is the first stable value in s, and also see that s(2) cannot change any further.
Step 2 has j = s(2) + 2 = 3+2 = 5. Hence, s(2) + s(5) = 3+5 = 8 → s(5). The stable terms in s are the first 3, i.e., {1, 3, 3}.
Step 3 has j = s(3) + 3 = 3+3 = 6. Hence s(3) + s(6) = 3+6 = 9 → s(6). The stable terms in s are the first 4, i.e., {1, 3, 3, 4}.
Number of edits.
Zizka [1] writes about change applied to s(20); in the quote we have changed the designation of the sequence s to match this paper:
“In step 4 the term at position 4 + s(4) = 8 is changed to 8 + s(4) = 12; in step 8 the term at position 8 + s(8) = 20 is changed to 20 + s(8) = 32; in step 10 the term at position 10 + s(10) = 20 is changed to s(20) + s(10) = 32 + 10 = 42.”
Hence, step i = 8: 32 → s(20), then step i = 10: 42 → s(20). We may say then that j = 20 has trajectory {20, 32, 42} and the cardinality of change to s(20), c(20) = 2, as s(20) has changed twice.
Zizka observed that j = 20 is the least j with c( j) = 2. Klaus Brockhaus identified c(3498) = 3 and is the least j with c( j) = 3. Rémy Sigrist found c(1024914) = 4, the least j with c( j) = 4.
Immutability of s( j).
It is clear that s(20) cannot change in steps i > 19, however s(20) is immutable well before step 19, since m = 1 appears only once in the sequence at s(1). Clearly s(n) ≥ n, and since f(i): s(i) + s( j) → s( j), there is some displacement d ≥ 1 such that s( j) is immutable at step (i − d).
Table 2.1 concerns the smallest j such that s( j) has c( j) = k edits:
k j values of s(j)
--------------------------------------
0 1 {1}
1 2 {2, 3}
2 20 {20, 32, 42}
3 3498 {3498, 5917, 8293, 10042}
4 1024914
...
The scatterplot in Figure 1 suggests that s(p) is prone to immutability. Indeed, given 218 terms of s, the prime indices p such that s(p) receives 1 change include {2, 5, 13, 197, 337, 9533, 56519}. Only s(2) = 3 and s(56519) = 91951 are prime.
Given the same terms, we find that 2k for odd k change once. In fact, regarding p in the list of primes that receive change, it seems that pk changes once for odd k, and that for even k, pk is immutable. Furthermore there seems to be a pattern in s(2k) = 2(k−1) × 3. This seems to generalize to s(pk) = p(k−1) × s(p).
Additionally, it seems that s(qk) for prime q not listed above is immutable for any k ≥ 0.
Cardinality k(m) of m in s.
Table 2.1 shows the least m such that m appears k times in s, at s(n) given 224 terms in s
k m n
--------------------------------------
0 2
1 1 {1}
2 3 {2, 3}
3 21 {13, 14, 21}
4 231 {106, 143, 154, 231}
5 9471 {4346, 5819, 5863, 6314, 9471}
6
558789 {249249, 256414, 343321, 345917, 372526, 558789}
...
(Work in progress.)
Appendix:
Block[{s, nn = 2^12},
s = Range[Max[3, IntegerLength[nn]] nn];
Do[s[[i + s[[i]]]] = s[[i + s[[i]]]] + s[[i]], {i, nn}];
s[[1 ;; nn]] ]
This code can produce 224 terms in 82.1875 s on a machine with Intel Xeon E-2286M CPU @ 2.4 GHz and 32 GB RAM.
Concerns OEIS sequences:
A000027: The positive integers: a(n) = n for all n ≥ 1.
A137417: Limiting sequence: s(n) = n → at step i, s(i+s(i)) = s(i+s(i)) + s(i).
Document Revision Record.
2021 0804 2215 Created.