OEIS A333238
by Michael Thomas De Vlieger, St. Louis, Missouri. 2020 0328.
Abstract:
Consider the prime partition λ ⊢ n (a multiset of primes p whose sum is the positive integer n). Row n of OEIS A333238 lists the distinct least primes p of all prime partitions λ of n. This sequence derives from thoughts and correspondence with David James Sycamore. Herein we analyze some of the properties of this sequence, as well as related sequences. The analysis focuses on those n for which row n of A333238 lists primes with indices 1 … k, i.e., all the k smallest primes. We note that this range of primes produces a primorial P(k) = A002110(k), and that since the primes are distinct, we can create a compact notation A333259(n) of row n of A333238 that expresses the primes as 1s in the (k − 1)-th place of a binary number, converted to decimal. This work relates observations of primes p(k) and their relation to n.
Let us consider the prime partition of n, an integer partition λ wherein all parts are prime. For instance, [3 + 2] is a prime partition of the sum 5; for n = 5, [5] is also a prime partition. For 6, we have two prime partitions [3 + 3] and [2 + 2 + 2]. We note that there are no prime partitions for n ≤ 1. The number of partitions of n is shown by A000041(n), while the number of prime partitions of n is shown by A000607(n). We note that for all n > 0, A607(n) < A41(n).
We offer two methods (codes 1.1, 1.2) to generate the prime partitions of n = 12, in order to furnish the following example:
(Example 1.1): [7, 5], [7, 3, 2], [5, 5, 2], [5, 3, 2, 2], [3, 3, 3, 3], [3, 3, 2, 2, 2], [2, 2, 2, 2, 2, 2]
We may concern ourselves with lists of the least and of the greatest primes p among the prime partitions λ of n. Certainly for sufficiently large n, the occasion arises wherein we have multiple instances of primes p ≤ n, thus, we take the union of all the least and all the greatest primes to arrive at a list of the distinct primes p in either category. In Example 1.1, a list of least primes would include {5, 2, 2, 2, 3, 2, 2} and greatest {7, 7, 5, 5, 3, 3, 2}. Taking the distinct least primes we have {2, 3, 5}, while the distinct greatest primes leaves us with {2, 3, 5, 7}.
Distinct Least Primes of Prime Partitions of n
We define the sequence A333238 as an irregular triangle such that row n is a list of the distinct least primes p among the prime partitions λ of n. The least primes among the prime partitions of 5 are 2 and 5, cf. the 2 prime partitions of 5: [5] and [3, 2], thus row 5 lists {2, 5}. The least primes among the prime partitions of 6 are 2 and 3, cf. the two prime partitions of 6, [3, 3], and [2, 2, 2], thus row 6 lists {2, 3}. Row 7 contains {2, 7} because there are 3 prime partitions of 7: [7], [5, 2], [3, 2, 2]. Note that 2 is the smallest part of the latter two partitions, thus only 2 and 7 are distinct.
We can produce a table that plots prime p in row n at π(p) place (in colored boxes), with interposing primes q missing from row n shown in unhighlighed italics as a place holder:
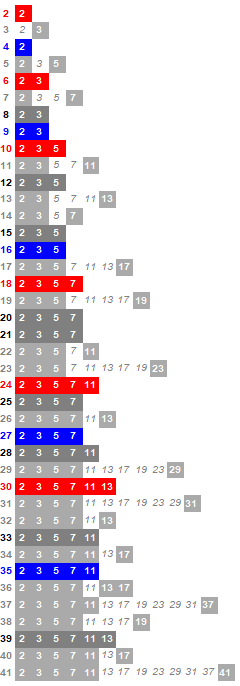
Figure 1.1
(View an extended chart of rows 2 ≤ n ≤ 240 at this link).
In Figure 1.1, we pick out those rows wherein we have a set of the smallest prime indices 1…k, whose product is a primorial P(k) = A002110(k). For the sake of concision and simplicity we shall refer to these rows as “primorials”. The smallest row n with P(k) is shown in red, with n appearing in A330507. The largest row n with P(k) is shown in blue, n appearing in A333417. Those rows n in a darker gray have interposing primorials P(k), neither the smallest n nor the largest.
Given Alois Heinz’s extended data at A333259, we can identify assured values for 1 ≤ k ≤ 450. Among these, we first encounter values 0 ≤ v ≤ 11 at {90, 146, 1, 2, 3, 4, 24, 28, 79, 241, 47, 205, …}. There are k that do not appear at all in A330507 and A333417 (i.e., k such that v = 0); these include {90, 151, 349, 352, 444, …} (per Alois Heinz), and k that appear only once (i.e., k such that v = 1), including {146, 216, 234, 236, 253, 261, 269, 288, 291, 318, 330, 357, 359, 360, 362, 373, 399, 410, 414, 432, 437, 438, 440, 442, …}. In extended data, we find k = 146 appearing at n = 2541, thus, we color row n = 2541 green, containing a solid set of primes with indices 1 ≤ i ≤ 146, and indeed at rows n in {2541, 4047, 4445, 4469, 4823, 5041, 5203, 5663, 5735, 6351, 6687, 7271, 7317, 7339, 7355, 7679, 8277, 8505, 8591, 9063, 9211, 9273, 9295, 9369, 9989, …}. We define an irregular triangle T where row k contains all indices n in A333238 for which we have prime indices 1 ≤ i ≤ k; we have data at A333259 sufficient to guarantee 450 rows. (Dataset appears here, with index offset 0; the indices are unlabeled.)
Since we are dealing with distinct primes p, and such are either included or not, we have a binary relation. We can thus write either 0 or 1 in the i-th position, where i = π(p). For example, in row n = 11 of A333238, we have {2, 3, 11}, which respectively have indices {1, 2, 5}, therefore we write 1 in the first, second, and fifth positions, zero in all others less than the largest index k to obtain {1, 1, 0, 0, 1}. We might reverse the order to obtain a binary number 10011, which is 19 decimally. Therefore, we write a second and more compact sequence A333259 encoding the primes in A333238 thus. (See code 1.3.) In this way, we can store a compact annotation of the primes in row n of A333238, as Alois Heinz had done in the 10,000 term data file at A333259. Let x = n and y = π(p). In this way we can produce a larger map showing 2 ≤ n ≤ 240 (here rotated counterclockwise for easy visibility):
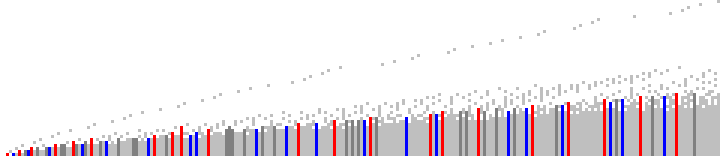
Figure 1.2
(
Take a look at an extended chart here but in the style of Figure 1.1.)
Some observations:
For prime p, we have the prime partition [p], therefore p appears as the greatest prime in row n of A333238, in Figure 1.1 the rightmost boxed prime, or in Figure 1.2, the “highest” pixel.
The plot (x, y) of the primes in row n, with y = n and x = π(p) has an interesting appearance (Figure 1.2 is such, rotated counterclockwise for convenience here).
We use a color code to color the plot at Figure 1.2 to show even n in red, odd n in blue, in Figure 1.3 below:

Figure 1.3
Now we show only even 2 ≤ n ≤ 480, and understandably the chart is red:

Figure 1.4
And odd 2 ≤ n ≤ 480 for an all-blue chart:

Figure 1.5
We note that all primes p > 2 are odd; this is the reason for “high flying” pixels in blue, representing prime p = n, above the mass of primes shown for odd n in Figure 1.5. In other words, we plot (p, p) = 1 for all prime n = p.
We note a “fringe” area in Figure 1.4, with a less-pronounced area in Figure 1.5, at which we have gaps amid certain primes, and below which we have a solid run of primes p in row n of A333238. As a consequence, it seems the “primorials” pertain only to a few even n: {0, 2, 4, 6, 8, 10, 12, 16, 18, 20, 24, 28, 30, 44, 60, 76}, with k in {0, 1, 2, 3, 4, 5, 6, 10}. The primorial P(1) = 2 is found only at even n, i.e., for n = 2 and n = 4. Conversely, primorials k > 10, when they appear in A333238, pertain to odd n. It would seem the “fringe” zone of primes for even n would guarantee that the sequences n = {0, 2, …, 60, 76} and k = {0, 1, 2, 3, 4, 5, 6, 10} are finite.
We can demarcate zones in the even (red) and odd (blue) plots in the following way.
For even: use a records transform (see code 1.4.) for the largest index k in n (topmost pixel in each column n of Figure 1.4), while using the run length of 1s in the binary notation of A333259(n) (see code 1.5.) to find the demarcation between the solid run of primes and the “fringe” primes. For odd, we ignore the “high flying” (p, p) primes then do same (see code 1.6, 1.5).
This is a chart of even n, showing the “fringe” primes in pink and the solid block as red, with dark red showing primorial n:
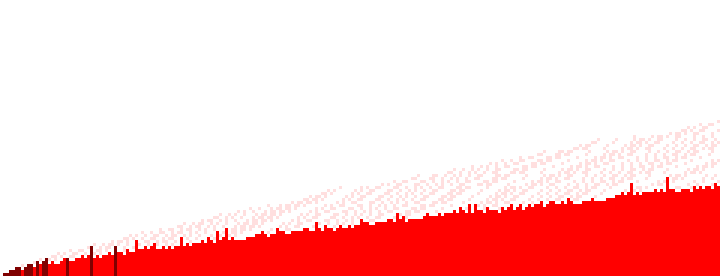
Figure 1.6
As regards indices registered vertically, we have the heights bounded by code 1.4, {1, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6, …}, and the solid-fringe demarcation bounded by the even terms generated by code 1.5 at indices {0, 1, 1, 2, 2, 3, 3, 2, 3, 4, 4, …}.
This is a chart of odd n, showing the “fringe” primes in light blue, the solid block as blue, with dark blue showing primorial n:
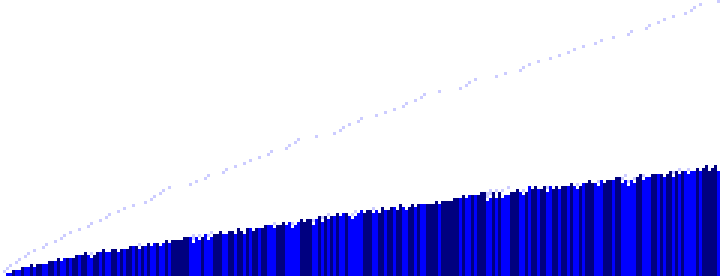
Figure 1.7
As regards indices registered vertically, we have the heights bounded by code 1.6, {0, 0, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, …}, and the solid-fringe demarcation bounded by the odd terms generated by code 1.5 at indices {0, 0, 1, 1, 2, 2, 2, 3, 3, 3, 4, 3, 4, …}. We see that these two sequences are more closely matched than they are for Figure 1.6.
Though interesting, the solid-fringe demarcation may not be helping us render a true relation. For this, we might examine a plot of (n, p) rather than (n, π(p)):

Figure 1.8.
From Figure 1.8 we see a pattern, at least among the even (red) fringe primes that seems to rationalize their appearance.
Labeling the primes p at (x, y) not as p but as x − y (and here rotating clockwise 90° to the original orientation in Figure 1.1) we can make a few remarks.
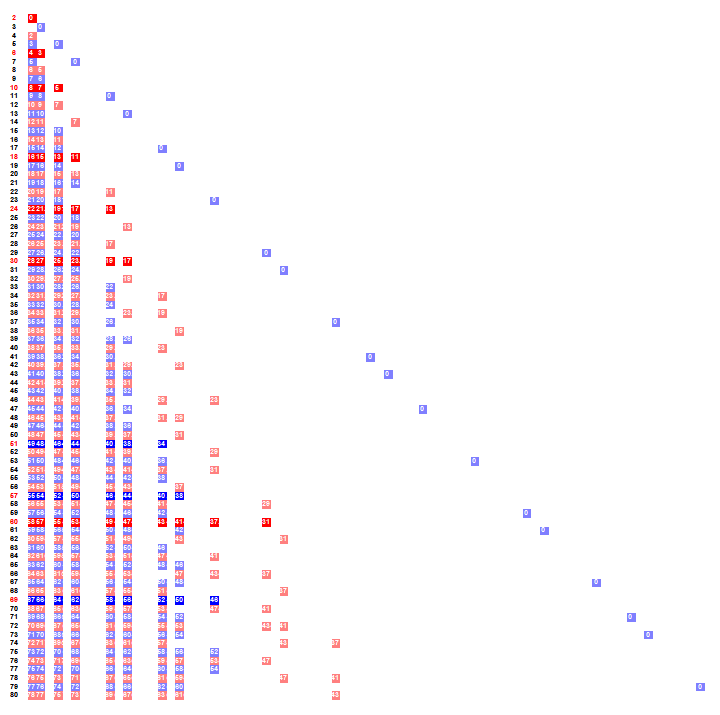
Figure 1.9
1. If x = y is prime p and (x − y) = 0, p appears in row x of A333238.
2. For x even, we have all prime (x − y) ≥ tx such that y is prime and t = ½. Example: for x = 32, we have {2, 3, 5, 7, 13};
32 − 3 = 29, 32 − 13 = 19. Note this does not explain the nonprime differences' appearance in row x even of A333238.
We do not have 11, since 32 − 11 = 21 is composite, however we have not identified the mechanism that admits 2, 5, 7 but not 11.
Clearly composite (x − y) ≥ ux with u > t also appear.
3. For x odd, we have all prime (x − y) ≥ tx with t = 2/3, once again there are composite (x − y) ≥ ux with u > t that also show.
The appearance of composite (x − y) remain unexplained. The plot below, continuing with the format of Figure 1.8, accentuates the “unexplained” terms:

Figure 1.10
We can also create a sequence u(n) = {0, 0, 0, 0, 0, 0, 1, 0, 1, 2, 1, 3, 3, 2, 1, 6, …} akin to A333259 for these unexplained terms. (Dataset for u(n) with 0 ≤ n ≤ 10000 here). Here is a plot of the largest even (red) and odd (blue) terms:
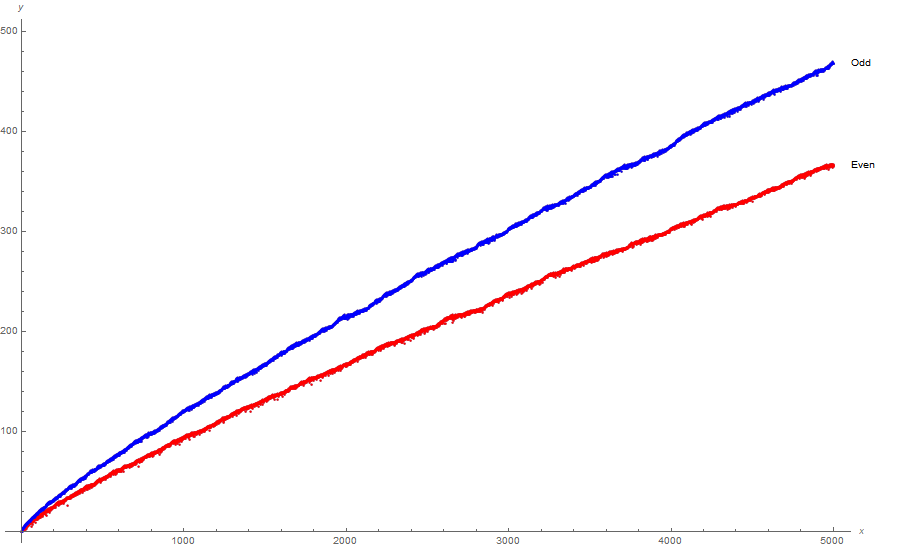
Figure 1.11
Distinct Greatest Primes of Prime Partitions of n
It would seem that the greatest primes p of the prime partitions λ of n are more easily explained. We return to Example 1.1, a list of least primes would include the greatest primes {7, 7, 5, 5, 3, 3, 2}, with the distinct greatest primes {2, 3, 5, 7}. We store these values in sequence g(n).

Figure 2.1
It is clear that for n odd, 2 is not a largest prime of the prime partitions of n, since we cannot compose n from a list of 2s. It is also clear that for n prime, we have the partition [n]. Further, for composite n = p + 1, p does not appear since 2 is the smallest prime. Here is an extended chart, produced by converting the indices of primes in row n of g(n) to a binary number:
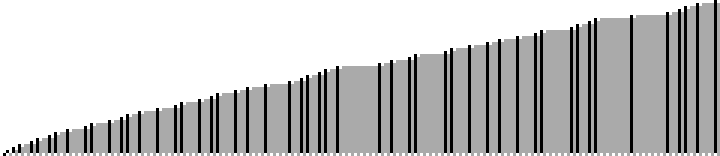
Figure 2.2
In this sequence, too, we might find primorials which appear for even n, identifying a first and last appearance, including singleton appearances. All primorials appear in a strictly increasing order in g(n).
Code 1.1: In Wolfram language we can find the prime partitions of n using the following code example pertaining to n = 12:
Select[IntegerPartitions[12], AllTrue[#, PrimeQ] &]
Code 1.2: The above intuitive approach proves less efficient than the following syntactically longer method:
primePartitions[m_] := Block[{s = {Prime@ PrimePi@ m}},
KeySort@ Merge[#, Identity] &@ Join[{0 -> {}, 1 -> {}}, Reap[Do[
If[# <= m,
Sow[# -> s]; AppendTo[s, Last@ s],
If[Last@ s == 2,
s = DeleteCases[s, 2];
If[Length@ s == 0,
Break[],
s = MapAt[Prime[PrimePi[#] - 1] &, s, -1] ],
s = MapAt[Prime[PrimePi[#] - 1] &, s, -1]
]] &@ Total[s], {i, Infinity}]][[-1, -1]] ]
]
Code 1.3: A333259: Let k be an index of the primes p listed in row n of A333238. Sum of 2(k − 1):
Block[{a, m = 59, s},
a = ConstantArray[{}, m];
s = {Prime@ PrimePi@ m};
Do[
If[# <= m,
If[FreeQ[a[[#]], Last@ s],
a = ReplacePart[a, # -> Append[a[[#]], Last@ s] ],
Nothing]; AppendTo[s, Last@ s],
If[Last@ s == 2,
s = DeleteCases[s, 2];
If[Length@ s == 0,
Break[],
s = MapAt[Prime[PrimePi[#] - 1] &, s, -1]],
s = MapAt[Prime[PrimePi[#] - 1] &, s, -1]]] &@ Total[s], {i, Infinity}];
{0, 0}~Join~Map[Total[2^(-1 + PrimePi@ #)] &, Rest[Union /@ a]]]
Code 1.4: Records transform A333259(n) for even n:
FoldList[Max, 1 + Rest@ Map[Floor@ Log2@ # &, a333259[[1 ;; 240 ;; 2]] ] ]
Code 1.5: Run lengths of 1s in the binary rendition of A333259:
Map[LengthWhile[Reverse@ IntegerDigits[#, 2], # == 1 &] &, a333259[[1 ;; 240]]]
Code 1.6: Records transform for b(n) = A333259(n) for odd n, with A333259(p) − 2(π(p) − 1) for n = prime p.
FoldList[Max, #] &@ Join[{0, 0}, Rest@
MapIndexed[1 + Floor@ Log2@ If[PrimeQ@ #2, #1 - 2^(PrimePi[#2] - 1), #1] & @@
{#1, 2 First[#2] + 1} &, a333259[[4 ;; 240 ;; 2]] ] ]
Code 1.7: Indices of “unexplained” primes in row n of A333238:
Block[{s = a333259[[1 ;; 120]]},
Table[MapIndexed[
Function[{k, j}, k (j) Boole[CompositeQ[i - Prime@ j]] /. 0 -> Nothing] @@
{#1, First[#2]} &, Reverse@ IntegerDigits[s[[i + 1]], 2] ] /. {} -> {0},
{i, 0, Length@ s - 1}]]
Code 2.1: The largest distinct prime parts p among the prime partitions λ of n include p(π(2 − [2 | n]))…p(π(n) − [isprime(n − 1)]) for n ≠ 3; for n = 3, the only distinct largest prime p = 3.
Array[Prime@ Range[2 - Boole[EvenQ@ #], PrimePi@ # - Boole[And[PrimeQ[# - 1], # != 3]]] &, 1200]
Concerns sequences:
A000041: Number of partitions of n.
A000607: Number of partitions of n into prime parts.
A002110: a(k) is the product of the smallest primes with indices 1 … k, i.e., the primorial P(k).
A330507: a(k) is the smallest positive integer n with the range 1 … k smallest primes in row n of A333238.
A333238: Irregular triangle with row n lists the distinct least primes p of the prime partitions λ of n.
A333259: Let k be an index of the primes p listed in row n of A333238. Sum of 2(k − 1).
A333337: Irregular triangle with row n lists the rows in A333238 that contain primes with indices 1…n.
A333417: a(k) is the largest positive integer n with the range 1 … k smallest primes in row n of A333238.
A333624
: Irregular triangle with row n lists the distinct greatest primes p of the prime partitions λ of n.
A333625: Let k be an index of the primes p listed in row n of A333624. Sum of 2(k − 1).
Document Revision Record.
2020 0327 1430 Created.