OEIS A334468
by Michael Thomas De Vlieger, St. Louis, Missouri. 2020 0501, modified 0505.
Introduction:
Consider OEIS A217287, length ℓ of a chain of consecutive integers starting with n, where each new integer in the chain has a prime factor q which no previous member in the chain has. In other words, starting from n, we consider the length ℓ wherein we encounter ensuing numbers n + 1, n + 2, …, n + ℓ − 1 whose prime decomposition introduces novel distinct primes q to a set of distinct prime divisors p of all such numbers encountered hitherto.
For example, we start with n = 1, which has no prime divisors (empty product). For n = 2, we introduce the factor 2. For n = 3, we introduce 3; these two are both prime; when we introduce a prime, we introduce a new prime factor q, thus, the chain lengthens. When we reach a perfect prime power, like n = 4 = 2², the chain terminates. Thus, ℓ(1) = 3.
Since n = 4 serves as the very same obstruction starting from n = 2, ℓ(2) = 2.
Beginning with n = 3, the number 4 introduces the factor 2 and does not obstruct, admtting access to 5, with 6 serving as the obstruction, thus ℓ(3) = 3, etc.
We can generate A217287 using Code 1.3, via encoding n as A087207(n) through Code 1.1, with a second but less efficient method Code 1.2.
Figure 1 below plots (n, ℓ(n)).

Tony Noe observed the following:
1. ℓ(n) ≥ 2.
2.
If n < 2 is prime or a prime power, ℓ(n) ≥ 3.
3.
For any n > 1, k > 1, ℓ(nk − n) ≤ n.
Neil Sloane added that ℓ(n) = least k > 0 such that n + k is k-smooth, i.e., that has no prime divisor q > k.
We observe additionally that ℓ(2k − 2) = 2, since 2k − 2 is even, and the distinct prime divisor of 2k is 2, which does not contribute new primes to the set of distinct prime factors of the chain that starts with 2k − 2. Therefore we have minima at {2, 6, 14, 30, 62, 126, 254, 510, …}, i.e., terms in A000918.
Maxima are {3, 4, 5, 8, 9, 11, 14, 18, 19, 20, 22, 25, 30, 32, …} in A217288, their indices {1, 4, 7, 16, 36, 79, 106, 222, 456, 460, 650, 1046, 1090, 2110, 2205, 2302, 3455, …} in A217289. We can compute the former via Code 1.4, the latter by Code 1.5.
We also note in Figure 1 the jumping of ℓ(n) to a number only for the function to decrement strictly to a point and pop again.
Let's look at numbers m in the chains starting from n as set out by A217287. These m are listed in row n of the irregular triangle T(n, k) at A217438. We note that T(n, 1) = n and row n has length ℓ(n).
Triangle begins:
1 2 3
2 3
3 4 5
4 5 6 7
5 6 7
6 7
7 8 9 10 11
8 9 10 11
9 10 11
10 11 12 13 14
11 12 13 14 15
12 13 14 15
13 14 15
14 15
15 16 17
...
We note the zig-zag or stair step pattern toward the upper right of the line (n, n).
Figure 2 below justifies the plot in Figure 1, placing ℓ(n) “on” pixels starting from pixel (n, n) to produce a raster. In other words, we plot numbers m in rows n of irregular triangle A217438 in black, with all other pixels left blank:

In the image we see the “obstructions” that appear as vertical borders of “on” pixels to the left, the first white pixel of the field to the right. This is the sequence s = {4, 6, 8, 12, 15, 16, 18, 24, 27, 30, 32, 36, 40, 45, …}. We see similar vertical “breakthroughs” where beginning from n allows a row of “on” pixels to stream past a previous barrier. These appear as horizontal borders of field above “on” pixels. The sequence of these is t = {3, 4, 7, 10, 11, 15, 16, 22, 25, 26, 31, 34, 36, …}. We note that s contains no prime number, since primes always admit a novel prime to the common set. The sequence t does admit primes, and seems sensitive instead to a number recently dropped. Perhaps t ought to instead be t – 1, since that is the number recently dropped by incrementing of n.
Figure 3 screens back the plot of A217438 in light gray, showing columns in s adjacent to terms in A217438 in red:

We propose a sequence s(n) = A334468(n) = primitive terms that are smallest numbers m = n + ℓ(i) that are ℓ(i)-smooth. In other words, if m is the last number in row n of A217438, s(n) lists in order any m + 1. Thus, s(n) constitutes a sequence of the “obstructions” mentioned in the examples above. The red pixels occur at (A334468(n), y). This sequence is generated by Code 1.6. All terms in this sequence are composite, since prime q always admits a novel prime (i.e., q) to the chain described above and at A217287.
Figure 4 again screens back the plot of Figure 2 in light gray, accentuating rows in t that are not adjacent to terms T(n − 1, k) in red, retaining the red-highlighted pixels of Figure 3 instead in yellow for comparison:

A second sequence t(n) = A334469(n) addresses the horizontal rows that include blue pixels at (x, A334469(n)). The sequence A334469(n) then is simply the indices of first differences d ≥ 0 of ℓ(n) (see Code 1.8). We may generate this sequence via Code 1.7 or Code 1.9.
Using Code 1.3 to generate over 222 terms of ℓ(i) (4323295 to be exact), we can produce 36960 terms of s(n). Taking first differences of s(n) to obtain u(n) = {4, 2, 2, 4, 3, 1, 2, 6, 3, 3, 2, 4, 4, 5, 3, 6, 6, …}. Define v(n) as maxima of u(n):
4, 6, 9, 12, 14, 16, 20, 24, 36, 42, 48, 51, 52, 55, 72, 75, 82, 84, 85, 86, 89, 92, 94, 104, 115, 117, 120, 133, 142, 144, 158, 162, 180, 195, 198, 204, ...
Define w(n) as least indices of the maxima of u(n):
1, 8, 25, 30, 54, 102, 166, 187, 287, 791, 1264, 1580, 2126, 2174, 2502, 4049, 6102, 6738, 9370, 9739, 10136, 10446, 10466, 10844, 12985, 20968, 24310, 27115, 31322, 36448, 42743, 45714, 56259, 60960, 107999, 108395, ...
Examining the prime decomposition of terms m in s(n), we note that all are composites with relatively small prime factors p. We define π(gpf(s(n))) as the sequence A333518(n) of indices of the greatest prime factors of s(n). The following table shows the smallest term s(j) with greatest prime factor p(i), i.e., A333518(j). Here, we define r(i) as the numbers s(j).
i p(i) j ω Ω r(i)
-----------------------------------
1 2 1 1 2 4
2 3 2 2 2 6
3 5 5 2 2 15
4 7 18 2 3 63
5 11 59 3 4 308
6 13 49 3 4 234
7 17 68 3 3 374
8 19 84 2 3 475
9 23 292 3 5 2392
10 29 401 2 4 3625
11 31 518 3 3 4991
12 37 791 4 4 8547
13 41 614 3 5 6232
14 43 615 3 3 6235
15 47 1153 3 5 13912
16 53 1221 4 4 14946
17 59 2654 3 6 39825
18 61 1220 3 4 14945
19 67 2646 3 6 39664
20 71 4965 4 4 87685
21 73 5499 2 3 99937
22 79 4931 4 6 86900
23 83 5879 4 4 108647
24 89 6994 5 5 135102
25 97 10109 4 6 214758
26 101 10444 4 5 223412
27 103 12322 4 5 274804
28 107 13343 4 5 304094
29 109 14088 3 3 325583
30 113 11256 3 9 245888
31 127 19523 4 6 488696
32 131 23472 5 6 614652
33 137 27295 5 6 741444
34 139 22588 4 6 586024
35 149 32147 4 4 908751
36 151 40572 4 6 1213436
37 157 41323 4 8 1240928
38 163 48489 4 5 1515085
39 167 43924 4 4 1340843
40 173 68859 4 6 2331175
41 179 77441 5 5 2692518
42 181 70471 4 6 2398250
43 191 61084 5 6 2016196
44 193 94726 4 6 3449875
45 197 75033 4 6 2589368
46 199 94725 4 6 3449864
47 211 75034 4 7 2589392
...
Figure 5 is a logarithmic plot of r(n).
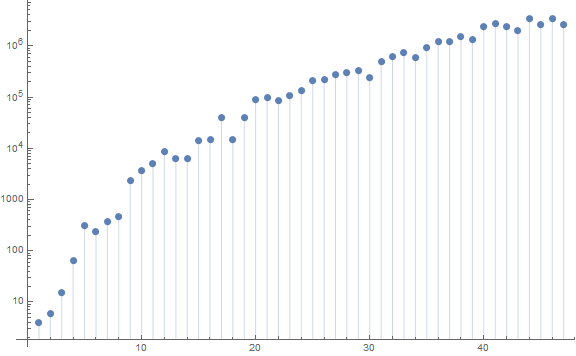
First positions of ω(m) = i distinct prime divisors of m in s generally seems to correspond with primorial P(i) for 2 ≤ i ≤ 7, but notably not i = 5, 2310 is not found in A334468(n) for 1 ≤ n ≤ 113891. Instead, the smallest m with ω(m) = 5 is 2730 = 2 × 3 × 5 × 7 × 13:
1 1 4
2 2 6
3 10 30
4 45 210
5 324 2730
6 2134 30030
7 20224 510510
...
First positions of Ω(m) = i prime divisors with multiplicity of m in s corresponds with powers 2i:
Ω i s(i)
---------------------
2 1 4
3 3 8
4 6 16
5 11 32
6 19 64
7 32 128
8 53 256
9 91 512
10 156 1024
11 260 2048
12 439 4096
13 767 8192
14 1315 16384
15 2286 32768
16 3958 65536
17 6824 131072
18 11855 262144
19 20666 524288
20 36084 1048576
21 63108 2097152
22 111111 4194304
...
A similar study of the prime decomposition of terms in A334469 doesn't seem to prove as interesting.
Appendix.
Code 1.1: Binary encoding b(n) = A087207(n). This sums the mappings 2(π(p) − 1) across primes p | n:
Array[If[# == 1, 0,
Total[2^(PrimePi /@ FactorInteger[#][[All, 1]] - 1)]] &, 120]
Code 1.2: Binary encoding b(n) = A087207(n). This approach concatenates the bits [p | n] (Iverson brackets) for primes p | n to arrive at a binary number that we convert to decimal:
Block[{nn = 120, r}, r = Prime@ Range[PrimePi@ nn, 1, -1];
Table[FromDigits[#, 2] &@ Map[Boole[Mod[n, #] == 0] &, r], {n, nn}]]
Code 1.3: Generate ℓ(n) = A217287(n):
Block[{nn = 2^8, r},
r = Array[
If[# == 1, 0,
Total[2^(PrimePi /@ FactorInteger[#][[All, 1]] - 1)]] &, nn];
Array[Block[{k = # + 1, s = r[[#]]},
While[UnsameQ[s, Set[s, BitOr[s, r[[k]] ] ] ], k++]; k - #] &,
nn - Ceiling@ Sqrt@ nn] ]
Code 1.4: Records transform of ℓ(n) = A217288(n):
Block[{nn = 2^16, r, t},
r = Array[
If[# == 1, 0,
Total[2^(PrimePi /@ FactorInteger[#][[All, 1]] - 1)]] &, nn];
t = Array[Block[{k = # + 1, s = r[[#]]},
While[UnsameQ[s, Set[s, BitOr[s, r[[k]] ] ] ], k++]; k - #] &,
nn - Ceiling@ Sqrt@ nn]
Map[FirstPosition[t, #][[1]] &, Union@ FoldList[Max, t] ] ]
Code 1.5: Indices of records in ℓ(n) = A217289(n):
Block[{nn = 2^8, r},
r = Array[
If[# == 1, 0,
Total[2^(PrimePi /@ FactorInteger[#][[All, 1]] - 1)]] &, nn];
Array[Block[{k = # + 1, s = r[[#]]},
While[UnsameQ[s, Set[s, BitOr[s, r[[k]] ] ] ], k++]; k - #] &,
nn - Ceiling@ Sqrt@ nn] ]
Code 1.6: Generate A334468(n):
Block[{nn = 2^8, r},
r = Array[
If[# == 1, 0,
Total[2^(PrimePi /@ FactorInteger[#][[All, 1]] - 1)]] &, nn];
Union@ Array[Block[{k = # + 1, s = r[[#]]},
While[UnsameQ[s, Set[s, BitOr[s, r[[k]] ] ] ], k++]; k] &,
nn - Ceiling@ Sqrt@ nn] ]
Code 1.7: Generate A334469(n):
Block[{nn = 2^8, r},
r = Array[
If[# == 1, 0,
Total[2^(PrimePi /@ FactorInteger[#][[All, 1]] - 1)]] &, nn];
1 + Accumulate@ Tally[#][[All, -1]] &@
Array[Block[{k = # + 1, s = r[[#]]},
While[UnsameQ[s, Set[s, BitOr[s, r[[k]] ] ] ], k++]; k] &,
nn - Ceiling@ Sqrt@ nn] ]
Code 1.8: First differences of A217287(n):
Block[{nn = 2^8, r},
r = Array[
If[# == 1, 0,
Total[2^(PrimePi /@ FactorInteger[#][[All, 1]] - 1)]] &, nn];
Prepend[Differences[#], #[[1]] ] &@
Array[Block[{k = # + 1, s = r[[#]]},
While[UnsameQ[s, Set[s, BitOr[s, r[[k]] ] ] ], k++]; k - #] &,
nn - Ceiling@ Sqrt@ nn] ]
Code 1.9: Generate A334469(n):
Block[{nn = 2^8, r},
r = Array[
If[# == 1, 0,
Total[2^(PrimePi /@ FactorInteger[#][[All, 1]] - 1)]] &, nn];
Position[Prepend[Differences[#], #[[1]] ], _?(# >= 0 &)][[All, 1]] &@
Array[Block[{k = # + 1, s = r[[#]]},
While[UnsameQ[s, Set[s, BitOr[s, r[[k]] ] ] ], k++]; k - #] &,
nn - Ceiling@ Sqrt@ nn] ]
Concerns sequences:
A000918: 2n − 2, indices of minima (i.e., positions of 2) in A217287.
A087207: A binary representation of the primes that divide a number, shown in decimal.
A217287: Length of chains of numbers starting with n whose prime divisors divide at least one of the previous numbers in the range.
A217288: Maxima of A217287.
A217289: Indices of maxima of A217287.
A217438: Irregular triangle T(n, k) where row n lists numbers m in the chains described by A217287.
A334468: Primitive terms that are smallest numbers m = n + k that are k-smooth for k in A217287.
A334469: Indices of first differences d of A217287(n) such that d ≥ 0.
A333518: Indices of greatest prime factors of A334468(n).
Document Revision Record.
2020 0501 2200 Created.
2020 0502 1245 Added reference to A217438.
2020 0503 0930 Added gpf and first differences of A334468, maxima of the latter, the least indices of their maxima.
2020 0503 1300 Extended A217287 dataset to over 222 terms, and those of dependent sequences.
2020 0504 1630 Analysis of prime decomposition of m in A334468, A334469.
2020 0505 1430 Add A333518.