On the Schuster Sequences.
by Michael Thomas De Vlieger, St. Louis, Missouri. 2020 0701.
Abstract:
This work concerns a trio of integer sequence drafts of late June 2020 by Matt Schuster.
We define a sequence of pairs of primes S = {p, q} such that p + q ≡ 0 (mod b). We begin using the least prime not in the sequence, setting p = nextprime(d), and we select q as the smallest prime distinct from p not already in the sequence such that p + q ≡ 0 (mod b). In the case of the Schuster sequences, set b = 10 and let p, q be primes that exceed the greatest prime divisor d of 10 (i.e., 5). Therefore, the primes {2, 3, 5} are precluded from the sequence.
We study some aspects of its curious plot, which exhibits long runs of the same sign (mod 10).
Definition.
The sequence S begins: (see Code 1.1.)
{{7, 13}, {11, 19}, {17, 23}, {29, 31}, {37, 43}, {41, 59}, ...}.
From this sequence Schuster derives three integer sequences: T contains the first primes p in each pair, while U contains the last primes q in each pair. Therefore we have T as follows (see Code 1.1.):
{7, 11, 17, 29, 37, 41, 47, 61, 67, 71, 83, 101, 103, 113, 131, 137, 149, 157, 167, 179, 191, 197, 211, 227, 239, 251, 257, 271, 277, 281, ...}
The sequence U begins (see Code 1.1.):
{13, 19, 23, 31, 43, 59, 53, 79, 73, 89, 97, 109, 107, 127, 139, 163, 151, 173, 193, 181, 199, 223, 229, 233, 241, 269, 263, 349, 283, 359, ...}
Finally, we have sequence V, where V(n) = | (q − p) |. (see Code 1.2.) This sequence begins:
{6, 8, 6, 2, 6, 18, 6, 18, 6, 18, 14, 8, 4, 14, 8, 26, 2, 16, 26, 2, 8, 26, 18, 6, 2, 18, 6, 78, 6, 78, ...}
Schuster had concluded that the plot of V is visually interesting, assigning a “look” keyword to it upon submittal.*
Figure 1.1: plot of 104 terms of V.
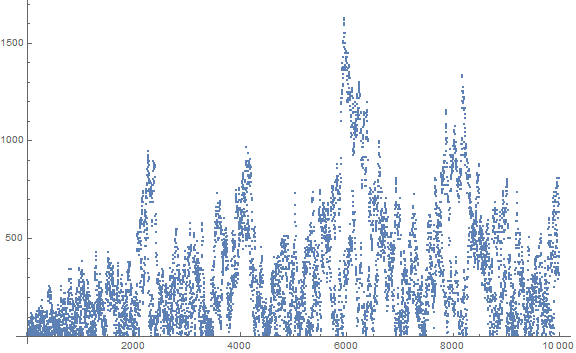
Figure 1.2: plot of 105 terms of V.
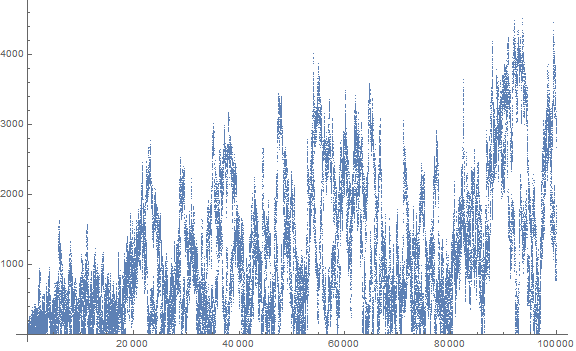
The plot has the aggregate appearance of “fire” or perhaps wood grain. The appearance subtends across scale.
Alternative Settings.
It is true that the bases of the Schuster sequences could be altered. For instance we might choose b = 6 or 14 and obtain different versions of S. For instance, for b = 6, we have S6 = {{5, 7}, {11, 13}, {17, 19}, {23, 31}, {29, 37}, {41, 43}, …}, while for b = 14, we have S14 = {{11, 17}, {13, 29}, {19, 23}, {31, 53}, {37, 47}, {41, 43}, …}. There is also no reason to select from primes p > d; we might select the least nondivisor prime, thus, for b = 10 or 14, 3, and derive a version of S. With b = 10 and starting with p = 3 (avoiding 2 and 5), we get {{3, 7}, {11, 19}, {13, 17}, {23, 37}, {29, 31}, {41, 59}, {43, 47}, …}.
Furthermore we might entertain what we could construe as the “simplest” version of S, that is, with b = 3 and beginning with p = 5: {{5, 7}, {11, 13}, {17, 19}, {23, 31}, {29, 37}, {41, 43}, …}, which is the same as S6 above. We note that a sequence S2 with b = 2, we obtain a sequence of paired consecutive odd primes {{3, 5}, {7, 11}, {13, 17}, …}, and as a consequence of all primes p > 2 being odd, the sequence of difference V2 is the infinite sequence of zeroes, i.e., OEIS A4.
Each of these alternatives (aside from S3 = S6) has a distinct and interesting plot. Generally, those of S3 (S6) are “tighter” than that of S10, while S14 appears comparable but distinct from S10. Examining S sequences for the primorials P(k) = OEIS A2110(k), there are interesting patterns as k increases that perhaps merit separate examination.
We acknowledge that any of these sequences might merit similar attention and perhaps yield similar conclusions.
For the purposes of this work, we set aside the consideration of alternatives and focus on S as Schuster had originally conceived, based on b = 10 and starting with p = 7 to continue only with greater primes.
Basic Aspects of Congruence.
Recall that the definition of the Schuster sequences include the module b = 10, beginning with prime p = 7. Schuster's rationale did not seem to have the reason to avoid the occasion of starting, say, with prime divisors of b, i.e., p = 2 or 5 and then not finding a prime q such that (p + q) ≡ 0 (mod 10). However, beginning with p > d, we have avoided the occasion with the collateral damage of also discarding p = 3.
Let us examine the properties of the Schuster sequences as residues (mod 10). It is clear that, as we are restricted to necessarily odd primes greater than 5, the residues with which we are dealing are those in the reduced residue system (RRS) of 10, i.e., {1, 3, 7, 9}, which, in terms of additive symmetry, boil down to {±1, ±3} (mod 10).
The residues of T, U, and V (mod 10) enjoy bijection:
T U V
----------
+1 -1 -2
+3 -3 +4
-3 +3 -4
-1 +1 +2
The consequences of this include the fact that V contains even numbers m ≢ 0 (mod 10). Another consequence merits coverage after the following images.
Figure 3.1 assigns same colors to the plot of V(n) for 1 ≤ n ≤ 360. The color of each point V(n) is determined by T(n) (mod 10). Red represents T(n) congruent to +1, orange +3, while light blue represents −3, violet −1, (mod 10).
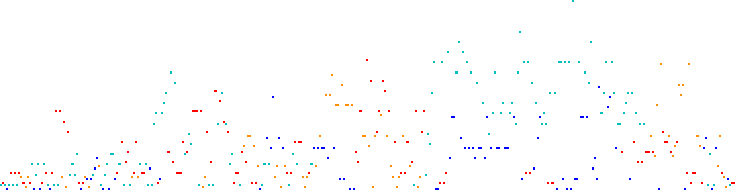
In Figure 3.1, we observe the effects of the bijection of residues; the color code for the residue in T appears in rows corresponding as noted to V(n) (mod 10), which is another consequence of the bijection. We can plot Figure 3.1 using Code 3.1.
Run Lengths of Polarity
Figure 4.1 assigns color to the plot of V(n) for 1 ≤ n ≤ 104. The color of each point V(n) is determined by T(n) (mod 10). Red represents T(n) congruent to +1, orange +3, while light blue represents −3, violet −1, (mod 10). (Click here for an enlarged plot of 105. See Code 4.1)
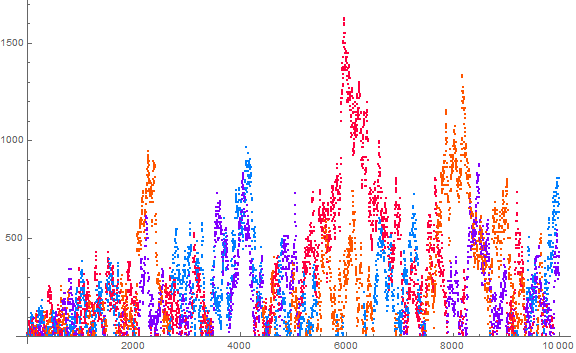
The image so plotted belies the fact that there are large runs of the same polarity of residue r (mod 10) in T (and in inverse, in U).
Let us derive a sequence of residues R (mod 10) from T (knowing that the residues of U are the inverse of R):
S: {7, 11, 17, 29, 37, 41, 47, 61, 67, 71, 83, 101, 103, 113, 131, 137, 149, 157, 167, 179, ...}
becomes
R: {-3, 1, -3, -1, -3, 1, -3, 1, -3, 1, 3, 1, 3, 3, 1, -3, -1, -3, -3, -1, ...}
Furthermore, we may take partial sums of R to obtain W:
W: {-3, -2, -5, -6, -9, -8, -11, -10, -13, -12, -9, -8, -5, -2, -1, -4, -5, -8, -11, -12, ...}
We can compute these using Code 4.2.
Figure 4.2 is a plot of R(n) with 1 ≤ n ≤ 10000:
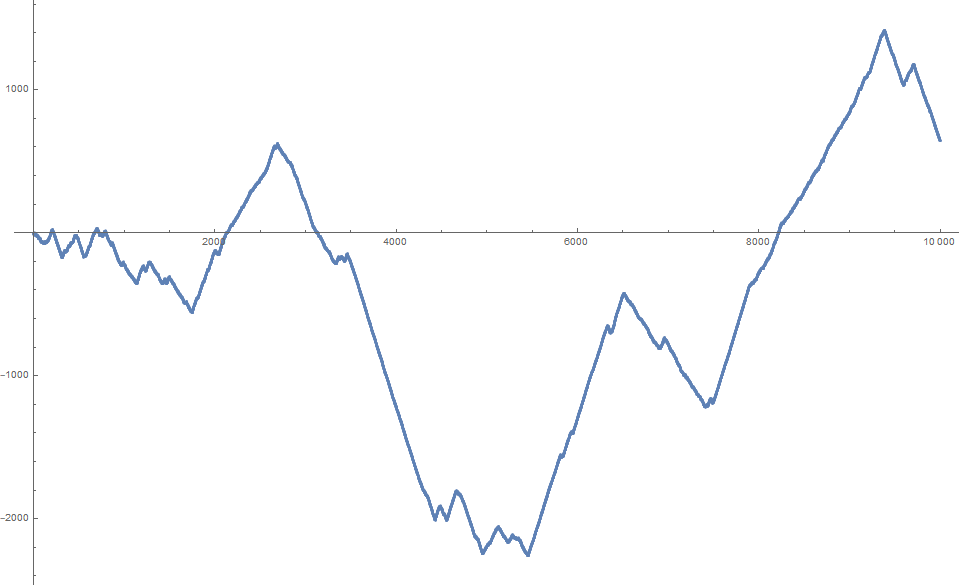
Figure 4.3 is a plot of R(n) with 1 ≤ n ≤ 106:
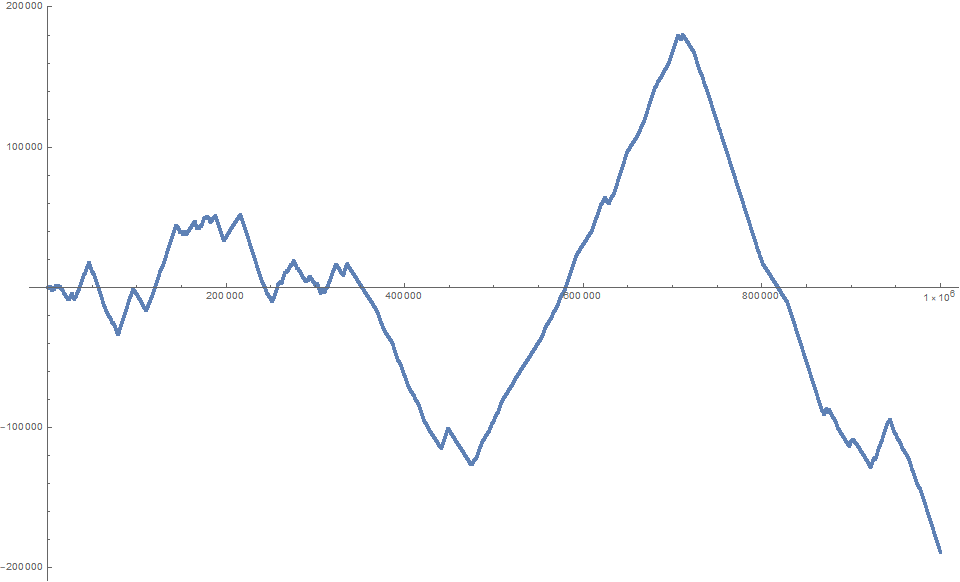
The run lengths R' of the signs in R illustrate the predominance of warm colors (indicating positive) and cool colors (negative) in Figure 4.1. The odd indexed terms pertain to negative and even positive polarity in W:
{1, 1, 3, 1, 1, 1, 1, 6, 5, 1, 1, 1, 2, 1, 1, 1, 1, 5, 4, 1, 1, 2, 1, 1, 4, 1, 8, 1, 1, 1, 1, 2, 1, 4, 1, 2, 6, 1, 4, 1, 1, ...}
We might analyze R' using a records transform. The records are:
{1, 3, 6, 8, 9, 28, 38, 48, 58, 61, 73, 781, 782, 1315, 1795, 2844, 3507, 4764, 5564, 6289, 6344, 8020, 19684, 42548, ...}
The indices of records are:
{1, 3, 8, 27, 64, 94, 101, 710, 722, 752, 1038, 1371, 9146, 10347, 12704, 12766, 14645, 14851, 19090, 19152, 27764, 28960, 58111, 241211, ...}
The run lengths W' of the signs in W illustrate the predominance of warm colors (indicating positive) and cool colors (negative) in Figure 4.1. The odd indexed terms pertain to negative and even positive polarity in W:
{192, 31, 450, 48, 1, 57, 21, 1328, 1, 1, 2, 1, 1, 7, 1, 990, 1, 1, 5082, 2354, 459, 1, 1950, 549, 1, 2, 1, 1, 1253, 1, 21281, 1, 20801, 1, 63643, 1, 123103, 1, 13641, 1, 46263, 1, 9759, 1, 39077, 1, 1, 228028, 1, 237633, ...}
Code 1.1: Generate 30 pairs of {p, q} of sequence S as described above.:
S = Block[{b = 10, d}, d = NextPrime@FactorInteger[b][[-1, 1]];
Nest[Append[#,
Block[{p = NextPrime[#[[-1, 1]]], q = d},
While[! FreeQ[#, p], p = NextPrime[p]];
While[Nand[FreeQ[#, q], Mod[p + q, b] == 0],
q = NextPrime[q]]; {p, q}]] &, {{d,
Block[{p = d}, While[Mod[d + p, b] != 0, p = NextPrime[p]]; p]}}, 30] ]
If we want T or U, we may employ part notation to extract it. For instance, storing above in variable S, we set T = S[[All, 1]] and U = S[[All, -1]], respectively.
Code 1.2: Generate 30 terms of sequence V(n) = | (T(n) − U(n)) |:
V = Map[Abs[Subtract @@ #] &, S]
Code 3.1: Code that generates all of above and plots V(n) with 1 ≤ n ≤ 360, color code according to R(n):
Block[{nn = 360, b = 10, d, m, R, S, T, V},
d = NextPrime@ FactorInteger[b][[-1, 1]];
S = Nest[Append[#,
Block[{p = NextPrime[#[[-1, 1]]], q = d},
While[! FreeQ[#, p], p = NextPrime[p]];
While[Nand[FreeQ[#, q], Mod[p + q, b] == 0],
q = NextPrime[q]]; {p, q}]] &, {{d,
Block[{p = d}, While[Mod[d + p, b] != 0, p = NextPrime[p]]; p]}}, nn];
T = S[[All, 1]];
V = Map[Abs[Subtract @@ #] &, S];
m = Max[V]/2;
R = Map[Mod[#, 10] &, T] /. {7 -> -3, 9 -> -1};
Magnify[#, 3] &@
ImageRotate@ Image@ MapIndexed[
ReplacePart[
ConstantArray[{1., 1., 1.}, m],
#1/2 -> Switch[R[[#2]],
1, {1., 0., 0.},
3, {1., .5625, 0.},
-3, {0., .75, .75},
-1, {0., 0., 1.}]] & @@ {#1, First[#2]} &, V] ]
Code 4.1: Code that generates all the sequences and plots V(n) with 1 ≤ n ≤ 1000, with color according to R(n):
Block[{nn = 10^3, b = 10, d, R, S, T, V},
d = NextPrime@ FactorInteger[b][[-1, 1]];
S = Nest[Append[#,
Block[{p = NextPrime[#[[-1, 1]]], q = d},
While[! FreeQ[#, p], p = NextPrime[p]];
While[Nand[FreeQ[#, q], Mod[p + q, b] == 0],
q = NextPrime[q]]; {p, q}]] &, {{d,
Block[{p = d}, While[Mod[d + p, b] != 0, p = NextPrime[p]]; p]}}, nn];
T = S[[All, 1]];
V = Map[Abs[Subtract @@ #] &, S];
R = Map[Mod[#, 10] &, T] /. {7 -> -3, 9 -> -1};
ListPlot[
Array[Style[V[[#]],
Switch[R[[#]], 1, Hue[1/12.], 3, Hue[11/24.], -3,
Hue[13/24.], -1, Hue[0]]] &, Length@ S],
PlotStyle -> PointSize[Small], ImageSize -> Large]
]
Code 4.2: Generate 30 terms of R and W from T:
R = = Map[Mod[#, 10] &, T] /. {7 -> -3, 9 -> -1};
W = a335805s = Accumulate@ R;
Concerns sequences:
T (Former A335805): Prime p in sequence S described above.
U (Former A335806): Prime q in sequence S described above.
V (Former A335807): | (q − p) | as described above.
* Dr. Neil Sloane recognized and supported the keyword “look” in personal correspondence, when the sequence V was slated to be A335807.
Document Revision Record.
2020 0701 1404 Created.
2020 0702 1630 Added code, links.
2020 0703 1900 Typos corrected.
2020 0820 1430 Modified to reflect alterations in the OEIS database.