OEIS A337099
A sequence by David Sycamore, this page written by Michael Thomas De Vlieger, St. Louis, Missouri, 2020 0826.
Abstract.
We examine a simple self-referential sequence that generates novel primes taken from the decimal digit sums of the immediate previous term, beginning with the first term 2. The examination regards the nature of features observed in the plot of this sequence, as well as computational approaches.
Contents:
Introduction.
Generation of a(n).
Computation.
Computation Alternatives and Optimization.
Analysis of a(n).
The Appearance of the Plot of a(n).
Conjectures.
Alternatives.
Appendix.
Introduction.
The sequence a(n) = A337099(n) starts with a(1) = 2, then, using s = decimal digit sum of a(n − 1), if s composite or if s already in the sequence, we append to the digits of prefix s a suffix t, that is, a term of A045572 possibly with a number of infixed zeros, so as to form the least prime p beginning with the digits of s not already in the sequence.
Generation of a(n).
There are two routes by which a prime p enters a(n):
1. Prefix s enters a(n) as s is prime and a(n) is free of s, i.e., s is a novel prime p.
2.
The concatenation of the digits of s and those of t (here noted s<>t) enters a(n) as the least prime not already in a(n) whose decimal expansion begins with the digits of s.
There are two ways that s<>t enters a(n):
1.
via composite s;
2.
via prime s where s already occurs in a(n) for m < n.
In both cases
there always shall be a suffix t that consists of digits of A045572(k), possibly left-padded with zeros so as to have j decimal digits, since all primes q outside of 2 and 5 appear in A045572.
Observe that, if s is not a novel prime p, then we append at least one decimal digit (comprising the suffix t). Therefore, single-digit primes p, i.e., 2, 5, or 7, may enter a(n) if and only p is the sum of digits of the preceding term a(n − 1). Because of this, we expect these numbers to appear in the sequence rather early.
The number 3 will not appear in a(n) since no single-digit prime may appear unless it is the sum of digits of the previous term, a prime, and the sum of digits of a prime written in decimal, outside of 3, does not occur. Therefore, the question of all primes appearing in a(n) must take into account the absence of 3.
What we are after in the case of either composite s or prime s already in a(n), is the formation of a novel prime p beginning with the digits of s through the addition of at least one digit in suffix t. This implies that t is not a number in standard notation, that is, t may feature one or more leading zeros.
Relevance of A045572 to A337099.
We look to A045572(k), integer k > 0, to furnish a series of its decimal digits (at times, preceded as necessary by a number of zeros), producing a suffix t so as to spell out a novel prime number p = s<>t in a(n). We know that, with regard to base b = 10, primes q such that gcd(q, 10) = 1 (i.e., nondivisor primes q necessarily coprime to 10) may only belong to certain residues r (mod 10). These are the reduced residues r, one of {1, 3, 7, 9} (mod 10). Any decimal digit may appear in higher ranks, with the highest rank precluding 0. Since at least 1 decimal digit of highest rank is furnished via s, we need not concern ourselves with ensuring t does not have leading zeros, in fact, it is at times essential that leading zeros are taken into consideration.
We might approach the suffix using two variables j = 1 and k = 1. The variable j governs the number of suffix digits, and advances when log10 k/4, while at same time k is reset to 1. Therefore the suffix t is A045572(k) padded left with zeros so as to have j digits.
We may compute A045572(k) (Formula 1):
A045572(k) = ½(5k + (3k + 2 mod 4) − 4).
Conversely we may find any term m in a(n) that is neither 2 nor 5 in A045572 via index k (Formula 2):
k = 4Q + (r + 1)/2 – [r > 5]
where Q is the quotient and r the remainder of m/10, and brackets are Iverson, the enclosed statement yielding 1 if true and 0 if false. In other words, Q = ⌊m/10⌋ and r = m mod 10. We might instead define Iverson [r > 5] as 1 – ((r mod 5) mod 2), if we dislike Iverson brackets.
Examples.
a(2) = 23 since the digit sum of a(1) is 2. Though 2 is prime, a(1) = 2, therefore we try appending the digits of A045572(1) = 1, but 21 is not prime; we try appending the digits of A045572(2) = 3; indeed 23 is prime thus, a(2) = 23.
a(3) = 5 since the digit sum of a(2) is 5, and 5 is prime and not in the sequence.
a(10) = 149 since the digit sum of a(9) = 95 is composite 14; we thus attempt to find the smallest single-digit term of A045572 that when concatenated with 14 produces a prime not in the sequence; this is A045572(4) = 9. Therefore a(10) = 149.
a(11) = 1409 since the digit sum of a(10) is again 14; having not found a prime for A045572(k) with k < 4, we thus attempt to find the smallest double-digit term of A045572 that when concatenated with 14 produces a prime not in the sequence; this is 0 prepended to A045572(4) = 9. Therefore a(10) = 1409.
We note that a(1) and a(3) are not found in A045572, but a(2) = A045572(10), a(10) = A045572(60), and a(11) = A045572(504) using Formula 2.
Computation.
The Twin Iterator Approach.
We compute the digit sum of a(n − 1) and store it in s; if s is a novel prime p, a(n) = p.
If s is composite or not a novel prime p, then we use the decimal digits of s as a prefix, i.e., the initial or highest-rank digits of the prime to be stored in a(n). We initialize two increment variables j = k = 1, the former governing the number of decimal digits in a suffix t and the latter the index of A045572(k) which furnishes nonzero digits so as to construct the least prime p not already in the sequence, via concatenation of the digits of s and those of t. Therefore both the primality test on s<>t and a determination of the presence of s<>t in a(n) is required to be satisfied, the least nature of the prime is guaranteed by induction on k and j in a special way.
We note that we start with j = k = 1, and that A045572(1) = 1. We test s<>1 to determine if this constructs a decimal prime number not in the sequence and if not, we increment k. Thus we move on to A045572(2) = 3, etc. We note that in A045572, there are 4 terms with 1 decimal digit, {1, 3, 7, 9}, then 40 with less than or equal to 2 digits {(0)1, (0)3, (0)7, (0)9, 11, 13, 17, …, 97, 99}, and 400 with less than or equal to 3 digits {(00)1, (00)3, (00)7, (00)9, (0)11, …, 997, 999}. This is quite simple to explain, therefore we use the pair of increment variables (j, k) in tandem. Upon an invalid s<>t, we set j = j + [j == log10 k/4] and k = k × [j < log10 k/4] + 1. Thus, for j = 1, k may advance to 4, but the next increment mst bring j to 2 and reset k to 1. For j = 2, k may advance to 40, then continue to j = 3 (resetting k = 1) and k as high as 400, etc. This way we prepend a sufficient number of zeros ahead of the digits of A045572(k) so as to compose a suffix t that when concatenated behind s yields the least novel prime p. (See Code 1.)
Computation Alternatives and Optimization.
Simple Incrementation.
We might have also simply used k as an increment on its own, without modification using A045572 and running to 10 j − 1. This would start with t = 1, but if s<>1 fails, would needlessly test s<>2 (forming an even number). It would be nearly as efficient to increment k = 1 by 2 and avoid even numbers. The method described above regarding A045572 is slightly more efficient than this approach.
Prefix Setting Memoization.
We might reduce time associated with generation of the sequence if we were able to store the last (j, k) for a given s already in the sequence. This way, instead of running primality and element testing on s<>t for all initial (j, k), we could pick up where we left off. For instance, we see that for a(10) = 149 = 14<>9, with (j, k) = (1, 4), we could have picked up these iterators when we re-encounter s = 14 for a(10). Instead of re-running (j, k) = (1, 1), appending 1 and finding 141 composite (again), then (j, k) = (1, 2) and appending 2 to find 143 composite (again), etc., we could merely increment k and pick up where we left off. Unfortunately, this would expand memory and lookup-time requirements, which might conspire to render the program too burdensome on memory and processor time for the optimization to be successful.
Term Annotation Method.
Another method is to put up the sequence in two parts, s(n) and t(n), where s(n) contains the prefixes, and t(n) the reversed suffixes (so as to preserve leading zeros). Let rev(x) be the function that reverses the decimal digits of integer x. Instead of searching for absence of s, we would determine the index i of the last occasion of s, then look up rev(t(i)), apply j = ⌊1 + log10 rev(t(i))⌋ and k = 4Q + (r + 1)/2 – [r > 5] to rev(t(i)) and initialize (j = j + [j == log10 k/4], k = k × [j < log10 k/4] + 1). This advances (j, k) to the next coordinate such that we pick up where we left off. Unfortunately, these gymnastics complicate the ordinary generation in the early stages of the sequence and necessitate the storage of additional data for each term such that it might only come in handy as n is large.
We have programmed an algorithm (see Code 2) that notes the term, s, and (j, k) so as to reduce generation time in a middle phase of generation, despite the fact we will suffer lookup delays as the record increases in length. Using the twin iterator approach (Code 1), it took about an hour to generate 10000 terms, but this was reduced to only 5 using this middle-phase generator. Code 2 required 5:20 hours to generate 100000 terms.
Indexed Last Successful Twin Iterator Method.
A third approach (see Code 3) involves storing prefix s as an index, and the last successful iterator pair (j, k) to reduce lookup time. Given 100,000 terms of a(n), there are only 37 prefixes s:
2, 4, 5, 7, 8,
10, 11, 13, 14, 16, 17, 19,
20, 22, 23, 25, 26, 28, 29,
31, 32, 34, 35, 37, 38,
40, 41, 43, 44, 46, 47, 49,
50, 52, 53, 55, 56
This approach generates 1000 terms in .28 s and 10000 terms in 21.34 s. Code 3 generates 100,000 terms in 3278 s. Pre-iteration of (j, k) complicates and delays execution; it is more efficient (as regards Wolfram language and this particular code) to allow the first suffix to fail for repeated prefixes. Code 3 is most effective even for dozens or hundreds of terms. The generation of 100,000 terms in under an hour perhaps puts a quarter million in striking distance (using Mathematica).
Suffix Preprocess and Lookup Approach.
A fourth approach involves generation and storage of u = A045572, then simply looking up the terms using a simple iterator k and dispensing with j, in place of concocting A045572(k) and padding left so as to have j digits. (See Code 4.1, requires Code 4.2) A simple lookup operation would replace the management of induction on (j, k) and the custom computation and recomputation of A045572(k). The values required may be reversed, i.e.,
1, 3, 7, 9
10, 30, 70, 90, 11, 31, 71, ..., 99;
100, 300, 700, 900, 110, 310, 710, ..., 999;
...
so as to “grab and go” rather than produce the terms during generation. (See Code 4.2) The associated lookup times and memory requirements come into play in any delays associated with this approach. However in this method, we merely iterate to the k-th term and find the suffix t in reverse. Relevant to this thoughtline, the greatest value of k in the generation of a(n) to 100,000 terms is 40000 at n = 93351, which would have instead been k = 44444 according to this method. Therefore the lookup table u would need to be nearly as large as the desired number of terms in order to suffice.
This approach should still be used in combination with prefix-iterator memoization so as to reduce testing time. A variant of this method stores the digits of the suffix to reduce reversal steps.
Oddly this method seems to require more time to generate a thousand terms than Code 3.
Circumventing the Self-Referential Nature of a(n).
Since a(n) is self-referential, the principal barrier to generating a large dataset is the need to constantly check a(n) for n large for the presence of s or s<>t. Reducing the searches via memoization prove helpful. It may prove helpful to first determine primality then, given a prime s or s<>t, we proceed to check if free. It remains necessary indeed to check if free since, very infrequently, p enters the sequence via concatenation fairly early.
A way to perhaps alleviate the burdensome non-membership test is to create a sort of annotation file.
Note that, for 10i ≤ p < 10(i + 1), dividing the interval into sub-intervals as to initial decimal digits d, for those prefixes s (which may be one or more digits) such that s is indivisible by 3, we find that the sub-intervals fill from least to greatest prime. There are limited lone primes produced early, but most primes in a(n) occur in a contiguous block. For instance, for n ≤10000, writing prime indices, we might delimit run lengths rather than list primes. Here, however we will list run lengths as starting and ending primes with a dash between them:
1, 3-59, 71-89, 101-113, 131-149, 163, 179, 191-139, 251-269, 281-293, 281-293, 311-317, 347-359, 373-389, 401-479, 491-599, 701-887, 1009-1193, 1301-1499, 1601-1789, 1901-2099, 2203-2399, 2503-2699, 2801-2999, etc.
This list is more compact. If we list primes that begin a run of ins and outs, noting the parity of the index, we can succinctly determine whether prime p is in a(n) without searching, say, hundreds of thousands of terms. When we enter a new p into a(n), we check the next and previous prime to p to see if we add it to an existing range, or break an even run (i.e., a run of not-ins) into two ranges. This annotation is relatively complex, but it would seem to be preferable to searching a long list of jumbled primes for membership, thereby speeding up the program. This has not yet been put into effect.
Let’s try to disentangle a(n) from its self-referential nature, at least partly alleviating the need to pour through a large list of values to find the next value.
We note some of the properties that will be explained later regarding the plot of a(n), most significantly, the “striation”, that is, the escalation of the primes p of the form that starts with the digits of prefix s (which is not divisible by 3) and a suffix t that consists of A045572(k) padded left by zeros so as to have j digits. Suppose s = 14. The striation associated with s = 14 is the infinite sequence {149, 1409, 1423, 1427, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 14009, 14011, …}. Therefore it is a sort of NextPrime operation sensitive to the fact that, if we generate a prime that does not have the first two decimal digits “1, 4”, we need to run NextPrime not on, say, 149, but 1400, or 14000 vs. 1499.
How do we know the trajectory of the striation associated with a given primitive s can proceed unobstructed? This is a paramount question; if it isn’t true, generation of the sequence without a full-sequence novelty test is not possible.
Indeed, certain primes appear early via a novel prefix (sum of digits). For instance, through composite first digits, we get 23 and 53 quite early. We have a(2) = 23 ← 2, but through a digit sum of 23, a(133) = 233 ← 1787; after the first ten thousand terms, s = 23 has appeared more than 900 times, more often than any other prefix. For a(4) = 53 ← 5, the prefix s = 53 first appears at a(75712) = 5303 ← 2978999. In both these cases, the prefix 23 derives itself from the prefix 2, which later generates prefix 29 as well. We know that the smallest prime q that sums to p is in A054750, but generally so as to simplify, we observe the largest decimal digit is 9, thus, division of s by 9 can serve as a starting point for how far we need to go in taking into account suffixes. It is reasonable to assume we might only need to consider single- and double-digit prefixes. Thus, we consider prefixes A001651 = {2, 4, 5, 7, 8, 10, 11, 13, 14, …} and need to take into account when a suffix like 23 arises from the striation associated with 2.
Outside of the generation of prime s2 through concatenation s1<>t for a prime s1 with fewer digits, nothing would seem to obstruct the striation associated with s2 outside of the (repeat) appearance of s2 itself, Therefore, it seems we may write a program in a completely different and non-self-referential way. When we have prefix s, we simply look up the last prime p generated by s and use a modified NextPrime function f(p) to produce the next term. This ought to vastly speed generation of the sequence even for relatively small n.
In having pursued this computation avenue, we find that we can generate 100,000 terms in .23 s and a million in 23. The problem is that we do indeed experience conflict between the prefixes s, according to their provenance according to digits. For instance, the suffixes 20, 22, 23, 25, 26, 28, and 29 are subsets of s = 2. Therefore the program must be modified to seek the smallest term that exceeds the greatest value stored in s. Thus far the algorithms have yet to be adjusted to incorporate this subroutine.
In having adjusted algorithms, we find that we might generate a(n) for 1 ≤ n ≤ 6185 error-free, but we have a conflict thereafter. This algorithm sums a(6185) = 100003 → s = 4, where the register s(4) = 433. However, s(40) has already been set to 4003 (a(5638) = 4003 ← 194989), thus it decides 4007 is the next term rather than the correct 439. Hitherto the assumption was that the program would reliably select the appropriate novel prime if it could create a larger prime than in all the related registers, i.e., those that were initial-digit parents or children of s. For s = 4, these would include {40, 41, 43, 44, 46, 47, 49} and {400, 401, 403, …, 497, 499}, etc., but since we had surmised we’d only need to calculate 2-decimal-digit prefixes, we merely consider the first range. The trouble is that s(40) = 4007 cannot truly interfere with s(4) = 433, since, according to its lexical interpretation, s(4) has already progressed beyond the former; the appropriate move would be to nextprime(433) → 439. Therefore a simple greater-than test is insufficient; we would need to account for the prefix of the number under consideration.
The application of so many constraints in this endeavor complicates the algorithm, slowing it. It may be more efficient, once corrected, to generate n > 105, and yet might be the only practical way to generate a million terms of a(n).
Analysis of a(n).
We might examine the first emergence of primes p and prefixes s in a(n).
Table 1 lists the prefix s, the number of instances of s, the first position m of s, value of a(m), and progenitor a(m − 1):
s pop m a(m) a(m-1)
----------------------------------
2 4 1 2 Given
4 11 15 41 211
5 33 3 5 23
7 109 28 7 43
8 146 5 83 53
10 331 13 101 1423
11 610 6 11 83
13 1045 40 13 823
14 1301 10 149 59
16 2202 25 163 1429
17 2919 18 17 89
19 4121 65 19 829
20 4519 86 2003 839
22 5910 119 223 1759
23 6799 133 233 1787
25 7690 159 251 1789
26 7695 258 263 1979
28 8014 303 281 1999
29 8101 553 293 19289
31 7589 722 31 17599
32 6905 912 3203 17789
34 5702 966 347 19699
35 5257 1138 353 19889
37 3822 2832 37 191899
38 3108 2901 383 191999
40 2014 5522 4001 194899
41 1646 7655 4111 196799
43 985 10601 4327 286999
44 658 10713 443 198899
46 338 12095 461 199999
47 237 30954 479 2919899
49 102 46369 491 2939899
50 53 46448 50021 2939999
52 13 68528 5209 2969899
53 11 75712 5303 2978999
55 1 92403 5501 2998999
56 1 93352 5623 2999999
...
We observe that the prefix s = 23 appears most often, 906 times, with n ≥ 10000, but for n ≥ 100,000, s = 29 has the maximum population of 8101.
Table 2 shows general data for a(n), 1 ≤ n ≤ 120. We note that m is the index of a(n) in A045572, that, since 2 and 5 do not appear in A045572, a(1) and a(3) is not found there:
n a(n) s < > t j k m
------------------------------
1 2 2 . . .
2 23 2.....3 1 2 10
3 5 5 . . .
4 53 5.....3 1 2 22
5 83 8.....3 1 2 34
6 11 11 . . 5
7 29 2.....9 1 4 12
8 113 11....3 1 2 46
9 59 5.....9 1 4 24
10 149 14....9 1 4 60
11 1409 14...09 2 4 564
12 1423 14...23 2 10 570
13 101 10....1 1 1 41
14 211 2....11 1 5 85
15 41 4.....1 1 1 17
16 503 5....03 2 2 202
17 89 8.....9 1 4 36
18 17 17 . . 7
19 809 8....09 2 4 324
20 173 17....3 1 2 70
21 1103 11...03 2 2 442
22 509 5....09 2 4 204
23 1427 14...27 2 11 571
24 1429 14...29 2 12 572
25 163 16....3 1 2 66
26 103 10....3 1 2 42
27 43 4.....3 1 2 18
28 7 7 . . 3
29 71 7.....1 1 1 29
30 811 8....11 1 5 325
31 107 10....7 1 3 43
32 821 8....21 1 9 329
33 1109 11...09 2 4 444
34 1117 11...17 1 7 447
35 109 10....9 1 4 44
36 1009 10...09 2 4 404
37 1013 10...13 1 6 406
38 521 5....21 1 9 209
39 823 8....23 2 10 330
40 13 13 . . 6
41 47 4.....7 1 3 19
42 1123 11...23 2 10 450
43 73 7.....3 1 2 30
44 1019 10...19 1 8 408
45 1129 11...29 2 12 452
46 131 13....1 1 1 53
47 523 5....23 2 10 210
48 1021 10...21 1 9 409
49 401 4....01 2 1 161
50 541 5....41 2 17 217
51 1031 10...31 2 13 413
52 547 5....47 2 19 219
53 167 16....7 1 3 67
54 1433 14...33 2 14 574
55 1151 11...51 2 21 461
56 827 8....27 2 11 331
57 179 17....9 1 4 72
58 1709 17...09 2 4 684
59 1721 17...21 1 9 689
60 1153 11...53 2 22 462
61 1033 10...33 2 14 414
62 79 7 9 1 4 32
63 1601 16...01 2 1 641
64 829 8....29 2 12 332
65 19 19 . . 8
66 1039 10...39 2 16 416
67 137 13....7 1 3 55
68 1163 11...63 2 26 466
69 1171 11...71 2 29 469
70 1049 10...49 2 20 420
71 1439 14...39 2 16 576
72 1723 17...23 2 10 690
73 139 13....9 1 4 56
74 1301 13...01 2 1 521
75 557 5....57 2 23 223
76 1733 17...33 2 14 694
77 1447 14...47 2 19 579
78 1607 16...07 2 3 643
79 1451 14...51 2 21 581
80 1181 11...81 2 33 473
81 1187 11...87 2 35 475
82 1741 17...41 2 17 697
83 1303 13...03 2 2 522
84 701 7....01 2 1 281
85 839 8....39 2 16 336
86 2003 20...03 2 2 802
87 563 5....63 2 26 226
88 1453 14...53 2 22 582
89 1307 13...07 2 3 523
90 1193 11...93 2 38 478
91 1459 14...59 2 24 584
92 191 19....1 1 1 77
93 11003 11..003 3 2 4402
94 569 5....69 2 28 228
95 2011 20...11 1 5 805
96 409 4....09 2 4 164
97 1319 13...19 1 8 528
98 1471 14...71 2 29 589
99 1321 13...21 1 9 529
100 709 7....09 2 4 284
101 1609 16...09 2 4 644
102 1613 16...13 1 6 646
103 11027 11..027 3 11 4411
104 11047 11..047 3 19 4419
105 1327 13...27 2 11 531
106 1361 13...61 2 25 545
107 11057 11..057 3 23 4423
108 1481 14...81 2 33 593
109 1483 14...83 2 34 594
110 1619 16...19 1 8 648
111 1747 17...47 2 19 699
112 193 19....3 1 2 78
113 1367 13...67 2 27 547
114 1753 17...53 2 22 702
115 1621 16...21 1 9 649
116 1051 10...51 2 21 421
117 719 7....19 1 8 288
118 1759 17...59 2 24 704
119 223 22....3 1 2 90
120 727 7....27 2 11 291
The Effect of Divisibility by 3 on a(n).
Furthermore we observe a pattern in s. Let the term “trine” refer to a number m that is congruent to 0 (mod 3), i.e., 3 | m, and “nontrine” a number that is congruent to 1 or 2 (mod 3), thus indivisible by 3; we define 0 as “trine”. We find that s such that s ≡ 0 (mod 3) (outside of 3 itself) does not occur, since the sum of decimal digits of prime q is never divisible by 3 (outside of 3 itself). This is because a trine sum of digits of q indicates divisibility of q by 3, contradicting the notion of prime q outside of 3 itself. This is well-attested in the Rules of 3 and 9 (decimal divisibility tests). This impacts the appearance of terms in a(n) that have initial digit combinations that would form a number s such that 3 | s. These terms are delayed in their appearance in the sequence because we need a digit sum s of a(n – 1) sufficiently large enough to produce the trine prefix s. This implies that for certain small s, we require very many terms of a(n) to see them, as s increases.
We note that primes that begin with 3-, 6-, or 9- are quite delayed in their appearance in a(n), and that 3 is not in a(n). For example, a(722) = 31, with progenitor 17599; a(2832) = 37 ← 191899. In order for prime 61 to appear, we must have progenitor whose digit sum is 61. These terms remain to appear in a(n) for n ≤ 100,000.
Table 3 shows the first position m of prime pi , along with progenitor a(m − 1), given the first 100,000 terms of a(n). We know 3 does not occur so we place a dash (−) in the third and fourth columns. We have yet to see primes 61, 67, and 97, etc., primes whose initial digit is indivisible by 3:
i p_i m a(m-1)
---------------------
1 2 1 .
2 3 - -
3 5 3 23
4 7 28 43
5 11 6 83
6 13 40 823
7 17 18 89
8 19 65 829
9 23 2 2
10 29 7 11
11 31 722 17599
12 37 2832 191899
13 41 15 211
14 43 27 103
15 47 41 13
16 53 4 5
17 59 9 113
18 61 . .
19 67 . .
20 71 29 7
21 73 43 1123
22 79 62 1033
23 83 5 53
24 89 17 503
25 97 . .
26 101 13 1423
27 103 26 163
28 107 31 811
29 109 35 1117
30 113 8 29
...
The Appearance of the Plot of a(n).
Figure 1: The plot of a(n) for 1 ≤ n ≤ 1000 features “clouds” associated with the first appearance of D-digit numbers in the sequence. The sequence D(n) lists the index of the first appearance of a d-digit number in a(n): {1, 2, 8, 11, 93, 1163, 10000, …}. These are respectively {2, 23, 113, 1409, 11003, 170003, 2300003, …}.
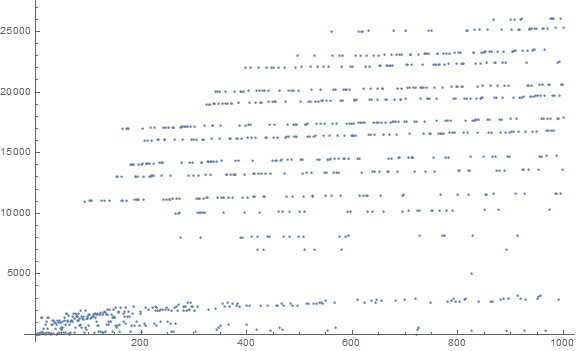
Striations.
The horizontal bands or “striations” are associated with the re-emergence of prefix s with a new suffix t that produces a strictly increasing new prime p = s<>t that is generally the next prime that begins with the digits of s. For instance, the rough row of points that begins at about y = 11000 (precisely, (x, y) = (n, a(n)) = (93, 11003)) pertains to the prefix s = 11. This striation begins with 11, then moves to 3 digits with 113, then to four with {1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193}, and finally, prominently in Figure 1, but parenthetically, beyond to n = 2194, a(n) = 11987:
{11003, 11027, 11047, 11057, 11059, 11069, 11071, 11083, 11087, 11093, 11113, 11117, 11119, 11131, 11149, 11159, 11161, 11171, 11173, 11177, 11197, 11213, 11239, 11243, 11251, 11257, 11261, 11273, 11279, 11287, 11299, 11311, 11317, 11321, 11329, 11351, 11353, 11369, 11383, 11393, 11399, 11411, 11423, 11437, 11443, 11447, 11467, 11471, 11483, 11489, 11491, 11497, 11503, 11519, 11527, 11549, 11551, 11579, 11587, 11593, 11597, 11617, 11621, 11633, (11657, 11677, 11681, 11689, 11699, 11701, 11717, 11719, 11731, 11743, 11777, 11779, 11783, 11789, 11801, 11807, 11813, 11821, 11827, 11831, 11833, 11839, 11863, 11867, 11887, 11897, 11903, 11909, 11923, 11927, 11933, 11939, 11941, 11953, 11959, 11969, 11971, 11981, 11987)}
These striations persist in a roughly linear fashion, gradually increasing as the digit which follows those of s in p proceeds from 0 to 9, after which point, the striation terminates, resuming in a level roughly an order of decimal magnitude higher. The more often the prefix s arises (certainly via the digit sum of the last term) the faster the striation exhausts itself. We see that the striation, and thus the cloud structure, roughly arranges itself according to n, but it needs not heed the decimal logarithm of n.
Ultimately we will see terms with 6 digits beginning with 110017, and 7 digits with 1100009, etc. This implies a clustering in the shape of a cloud, at a level gauged by the integer length of a(n), therefore an ever higher series of such clouds.
The striations appear to be paired since these pertain to prefixes s that are not divisible by 3.
Clouds via multiple-digit s.
Therefore, we observe clouds of striations generally gauged (but not strictly so) to the decimal logarithm of n.
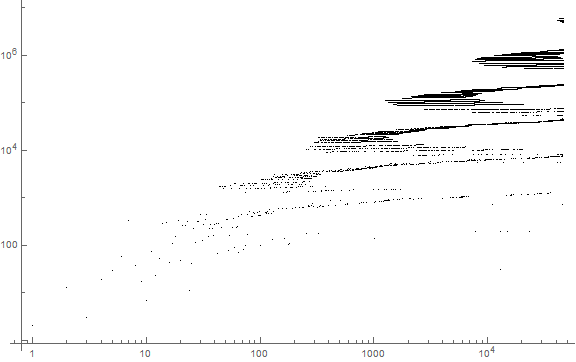
Figure 2: A log plot or a(n) for 1 ≤ n ≤ 10000:
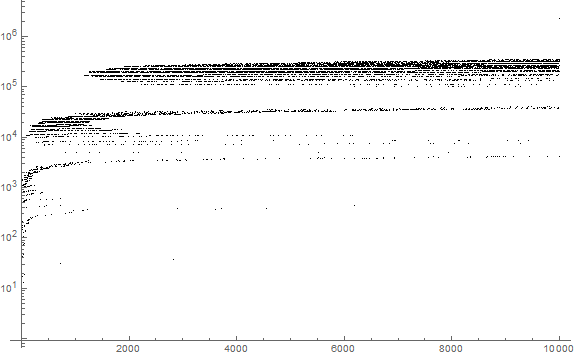
Figure 3: We colorize Figure 2 according to the first decimal digit of a(n) using a spectrum such that the digits 3, 6, and 9 correspond respectively with the primaries red, green, and blue. Furthermore, we accentuate the primaries at full saturation, yet the other digits appear at ¼ saturation.
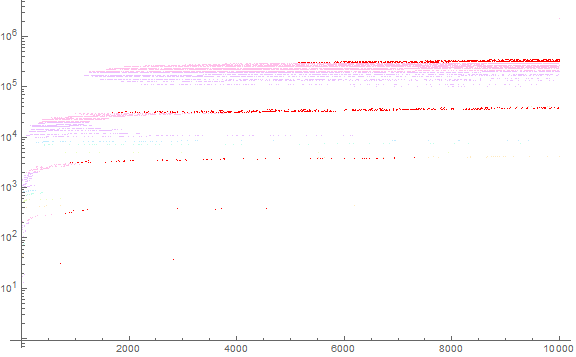
Thus, though s such that 3 | s does not occur, we see the clouds ever higher gradually edging into the “decimal forbidden digits” of 3, later certainly 6 and 9, because the digit sums s begin to enter the thirties, sixties, nineties, etc.
Table 4: We note that numbers that begin with 3 appear, but those that start with 6 or 9 have not (yet) appeared. Indeed, the first appearance of digits for 1 ≤ n ≤ 100,000:
D n a(n)
--------------
1 6 11
2 1 2
3 722 31
4 15 41
5 3 5
6 . .
7 28 7
8 5 83
9 . .
Figures that start with 6 or 9 have not appeared, since the prime digit sum s = 6 or s = 9 is impossible; we have to wait till we have a prime digit sum 61 for the former, and 91 for the latter. Having generated 100,000 terms of a(n), we estimate that 6 will appear within the range 100,000 ≤ n ≤ 200,000.
Figure 4 is a log-log plot of 100,000 terms of a(n) showing the cloud pattern continuing:
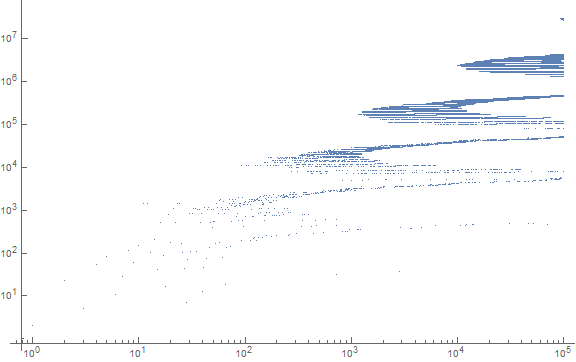
Table 5 shows the first position n of d-digit a(n), along with progenitor. We separate s from t with ".", though the number is not a decimal.
n a(n) a(n-1)
--------------------------
1 2 Given
2 2.3 2
8 11.3 29
11 14.09 149
93 11.003 191
1163 17.0003 29033
10000 23.00003 313637
93359 29.000039 3280961
...
Collapsing Clouds according to Most Significant Digit.
Let sequence d(n) = a(n)/10^⌊log10 a(n)⌋, that is, a(n) reduced to 1 ≤ d(n) < 10. Figure 5 plots d(n) with 1 ≤ n ≤ 1000, coloring points with 1 decimal digit blue, 2 cyan, 3 green, 4 gold, 5 red, etc. We see that the “clouds” indeed do fit into one another somewhat, not without limited intermingling.
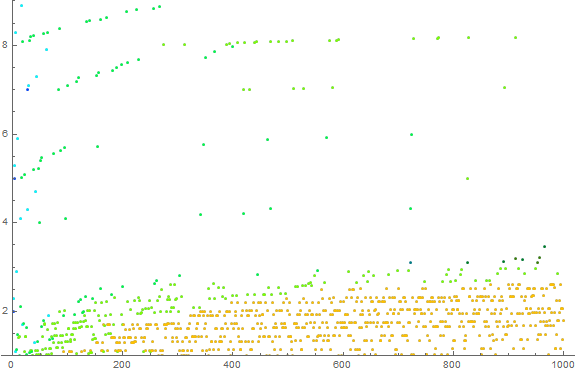
Table 6: We accentuate the only numbers that begin with digit 3 in a darkened color at right. These points pertain to the following:
n a(n) a(n − 1)
----------------------
722 31 17599
825 31...1 19489
892 31...3 16699
912 32..03 17789
926 31...7 19597
952 31..09 19687
957 32..09 19697
966 34...7 19699
These points belie the fact that such numbers result from the entry of a prime digit sum s (i.e., 31 = 1+7+5+9+9), then the occasion of the same prime already in the sequence necessitating concatenation with the smallest single-digit (in this case) term of A045572, until the single-digit possibilities are exhausted, then double-digit instances, etc. For a(912) = 3203, we see the composite digit sum s (32 = 1+9+4+8+9) with the necessary concatenation with t. Indeed this proves to be the source of the horizontal striations in the plots. We note that numbers beginning with “33” are missing as expected. These shall not show until there are preceding terms a(n − 1) whose digit sum s = 330.
Figure 6 is an extended plot of Figure 5 in the range 1 ≤ n ≤ 10000, based on Sycamore noting that higher clouds appear to fit within those pertaining to terms in a(n) with one fewer digit:

Again, we accentuate the terms in a(n) that begin with trine digits (here, solely 3). Remember that color in a reverse spectral order relates to increasing decimal integer length; we observe the striations continue across the boundaries of the “clouds”.
“High Flyers” via single-digit s.
Outside of the bulk of the “clouds”, we observe the occasion of high first-digit terms generated primarily early and scarcely, which we shall term “high flyers” for the sake of ease of reference in this work. Table 7 below shows such terms with 1 ≤ n ≤ 1000, generated on account of digit sums s = 5, 8, or 9:
n a(n) a(n - 1)
--------------------
3 5 23
4 5....3 5
5 8....3 53
9 5....9 113
16 5...03 41
17 8....9 503
19 8...09 17
22 5...09 1103
28 7 43
29 7....1 7
30 8...11 71
32 8...21 107
38 5...21 1013
39 8...23 521
43 7....3 1123
47 5...23 131
50 5...41 401
52 5...47 1031
56 8...27 1151
62 7....9 1033
64 8...29 1601
75 5...57 1301
84 7...01 1303
85 8...39 701
87 5...63 2003
94 5...69 11003
100 7...09 1321
117 7...19 1051
120 7...27 223
134 8...53 233
139 8...57 1061
152 7...33 2203
154 5...71 13001
156 7...39 13003
160 8...59 251
171 8...63 2213
182 7...43 14011
188 7...51 11113
197 7...57 11131
207 8...77 16001
209 7...61 2221
225 8...81 13103
229 7...69 2311
256 8...83 13121
266 8...87 10007
274 8..009 11213
312 8..011 10061
346 5...77 20021
350 7...73 20023
366 7...87 11311
389 8..017 20051
393 8..039 11321
399 7...97 22003
409 8..053 22013
420 7..001 421
421 8..059 7001
431 7..013 20113
439 8..069 22031
443 8..081 20123
462 5...87 10103
469 8..087 431
482 8..089 10133
498 8..093 23003
508 8..101 11411
510 7..019 10141
529 7..027 23011
569 5...93 20201
576 8..111 23021
580 7..039 22111
588 8..117 20231
592 8..123 10151
725 5...99 10211
728 8..147 10223
771 8..161 20411
774 8..167 23201
826 5..003 311
827 8..171 5003
893 7..043 313
913 8..179 3203
We see that eventually, j-digit suffixes t become exhausted in combination with the prefix s, then we turn to (j + 1)-digit suffixes, increasing the potential a(n) by an approximate order of decimal magnitude.
Nature of the Shape of the Clouds.
The clouds have a shape similar to a lunette or the well-known “swoosh” logo oriented so its smaller cusp is at bottom and the tail at top, slightly rising. We have noted in Table 1 the frequencies of prefixes s, that as n increases, the most frequent prefix s also increases (Table 8):
i s pop
3 17 103
4 23 906
5 29 8101
With a greater frequency comes a more intensive iteration of (j, k), making for a larger term, hence we see the most frequent prefixes responsible for the lunette shape. The lower cusp is shorter because these prefixes have generated over several clouds, while the cloud is only beginning to make headway among the larger prefixes s, making for a tail. The lower cusp tapers, since subsequent clouds can produce ever finer mantissas (according to logarithm base 10) via s = 10 concatenated with (j, k) with increasing j and low k. This said, we see prefix 10 infrequently and ever less frequently.
Figure 7 is diagrammatic, based on the premise of Figures 5 and 6, and accentuates the exponentially scaled clouds that are nested and in a lunette shape, where warmer colors are clouds of a higher number of decimal digits. The points are the high-flying primes that begin with digits 4, 5, 7, or 8. (the digit 9 is not shown for concision, since no term begins with 9 and will not appear for some time.)
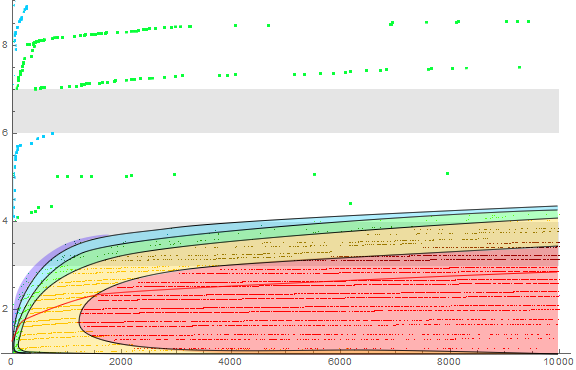
Furthermore it appears that the top surface of the clouds makes headway as n increases, so that eventually we shall see terms beginning with 4 and 5 more commonly as s increases over 39, and that there doesn't seem to be a barrier to the entry of the clouds into terms that begin with 6 or 9, though it may require a great number of terms to support their appearance. We have observed the invasion of numbers beginning with digit 3. Per A054750, we see that the smallest prime that generates a digit sum of 61 is 898999, but we observe values beginning with 8 relatively rarely. See Table 5 for the smallest d-digit terms in a(n).
The apparent rising horizontal striations are the entries of numbers associated with the few prefixes s. In this chart, there are only 27; since s cannot be divisible by 3, we see a void or gap. This notion leads us to consider circumventing the self-referential nature of a(n) as a way of rapidly calculating its terms.
“Digit Saturation.”
What happens when there are enough terms to fill the entire range of first-digits conveyed by Figure 6 and 7? It would seem that we would require more terms than we could reasonably generate. However, if we set the number base from b = 10 to b = 6 or b = 3, we would perhaps achieve a similar end.
Before we change bases, we would need to be conscious of the fact that nondivisor primes p only occur at the reduced residues mod b. Therefore, all primes p outside 2 and 5 for b = 10 are congruent to {1, 3, 7, 9} (mod 10), i.e., written in decimal, they end in one of those φ(b) = φ(10) = 4 digits, hence the relevance of A045572 to the case b = 10. For b = 6 (i.e., senary), there are only φ(6) = 2 possible end digits that harbor primes p outside 2 and 3, and those are 1 and 5. For b = 3 (i.e., ternary), there are only φ(3) = 2 possible end digits that harbor primes p ≠ 3, and those are 1 and 2. We see that the ternary case leaves us no “unforbidden” digits, since ternary numbers written conventionally (i.e., without leading zeros) must start with either 1 or 2.
Thus we define a6(n) analogously to a(n), except that the base we use is b = 6. We might start with any prime, but in this case we simply start with the first prime, as we had with b = 10. These are the decimal values of the first terms:
2, 13, 3, 19, 29, 59, 331, 37, 17, 7, 73, 23, 53, 293, 307, 43, 109, 149, 337, 47, 257, 263, 311, ...
but more usefully in terms of summing digits, we write them in senary (base 6):
2, 21, 3, 31, 45, 135, 1311, 101, 25, 11, 201, 35, 125, 1205, 1231, 111, 301, 405, 1321, ...
Figure 8 is a plot of a6(n) for 1 ≤ n ≤ 66 (i.e., 46656) in the character of Figures 6 and 7, exhibiting striations associated with prefixes that form clouds in a similar lunette shape. Since this image exhibits two-senary-digit prefixes s, we see that there are 6² = 36 combinations of the first two senary digits (less s such that 5 | s), therefore the striations for b = 6 appear grouped in fours. We see the smallest integer lengths exhibiting greater coarseness, and as the senary order of magnitude e increases, the striations seem to straighten out. We see where a striation jumps to the next order of magnitude, we reset the vertical position closest to s × 6e. These things are found in finer grain in the decimal plot, but are beautifully clarified here.
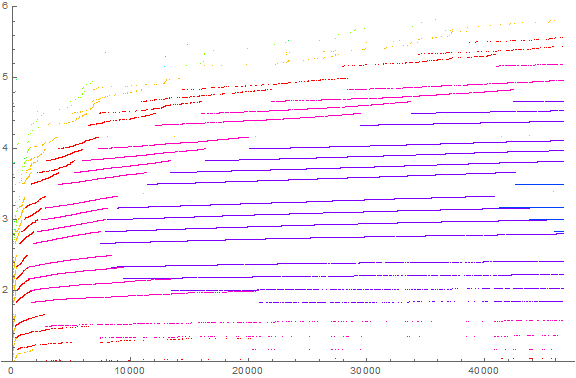
Figure 8 lends us a clue as to what we would see once the digit range is saturated. Indeed, the “digit range” has already been saturated once we have s > b. Indeed we are seeing a filling of the range b ≤ s < b² rather than 1 ≤ s < b.
Examining Figure 7, we see at left and most prominently at upper left, the “high-flyer” terms associated with single digit s, and we see these continue into the range wherein we see two-digit s come into play (i.e., the clouds).
Therefore we can expect the plot to intercalate triple-digit s horizontally and incorporating the longer-standing striations, and quadruple-digit s intercalated similarly, as n increases sufficiently. When three-digit s emerges with sufficiently large n, we should see such plotted between the lines of s = “10” (of any base) and s = “11” (of any base), i.e., s = “101” (written in any base). Therefore, if it were possible to include more terms in Figure 8, or, graphically, to “pan” or “page” right, we would see a group of four striations fitting between each of the striations (but two paired side by side in the “blank” area) in Figure 8. For a(n) (decimal), we would see two pairs of striations fitted between each two-digit-space, making for a very dense plot.
We define a3(n) analogously to a(n), except that the base we use is b = 3. We might start with any prime, but in this case we simply start with the first prime, as we had with b = 10. These are the decimal values of the first terms:
2, 13, 3, 7, 37, 223, 79, 2851, 1297, 5, 229, 2857, 1303, 2887, 11, 1381, 16921, 8209, 16927, 1549, ...
but more usefully in terms of summing digits, we write them in ternary (base 3):
2, 111, 10, 21, 1101, 22021, 2221, 10220121, 1210001, 12, 22111, 10220211, ...
Figure 9 is a plot of a3(n) for 1 ≤ n ≤ 310 (i.e., 59049) in the character of Figures 6 and 7. Due to the small nature of the number 3 and its perfect powers, the plot doesn’t seem very similar to that of a6(n) or a(n) (decimal). The striations do not seem to form clouds nor do they seem paired as they are in decimal, or in a group of 4 as in senary. The lunette shape appears to be absent, except that we do see a very shallow lunette whose center (associated with the highest-population prefix s) transitions so swiftly “upward” that subsequent lunettes appear to be cleaved in half.
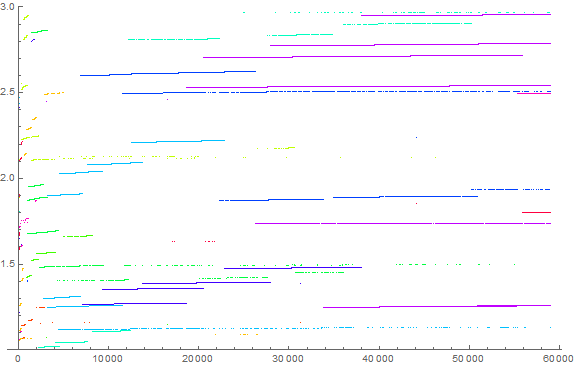
The thing to note about Figure 9 is that we have saturated one, two, and are working on 3 digit prefixes. Hence we might regard “(digit) saturation” merely as the transition between one-, two-, three-, or m-digit s expressed in base b.
Therefore, the 2-digit saturation of the decimal plot will be achieved when we see the first triple-digit prefix (i.e., digit sum) s, perhaps at around n = 1010. As n increases, the plot will begin to fill in starting from the bottom as three-digit prefixes emerge.
Thus, we can summarize all the major aspects of the plot of a(n).
1. The digit sums s = a(n − 1) such that q | (b − 1) does not divide s dare the font of the “striations”. These striations represent a subsequence of primes p (apart from p | b) whose base-b expansions begin with the digits d of s.
2. The striations beginning with s represent chains of primes that can be generated by a modified recursive nextprime(s × be) function that, whereupon the next prime would fail to begin with the digits d of s, would reset to nextprime(s × b(e + 1)). The chains with single digit s are generally suppressed by chains whose multiple digits d begin with the single digit s. The apparent length of the striations is governed by the frequency with which the sum s appears in a(n) for n across a given magnitude. Once all k-digit terms in the chain of s are exhausted, the striation “pops” to the next order of magnitude, seeming to form part of a cloud.
3. The striations seem to form “clouds”, especially given a sufficient number of D-digit s; their pairing or grouping pertains to the arrangement of reduced residues (mod b) since nondivisor primes p expressed in base-b may only end in digits belonging to those residues (mod b).
4. The “saturation” of the plot gives rise to an even denser series of clouds wherein the striations occur in a tighter formation related to the dendritic reduction according to the number of digits in s.
5. “Forbidden” D-digit prefixes s do not serve as a barrier to (D + 1)-digit s that begin with that forbidden digit, therefore the plot of the first digits of s will be filled.
Conjectures.
It seems assured (without rigor) that eventually we will have all primes p ≠ 3 in A337099, on account of the prime digit sums s of immediately preceding terms eventually entering the sequence. It is key to observe the smallest sums (on account of the digit sums of smaller numbers early in the sequence not fully covering), but in the production of many combinations of decimal digits as the sequence accumulates many terms, we should have all p in A337099 via attrition. Indeed some of these sums enter “early” via the concatenation function s <> t. These will be primes that begin with nontrine digits (1, 2, 4, 5, 7, 8). It seems, with 10000 terms of a(n), we are beyond the point where it might be that we wouldn’t fully cover the primes, say, 5 through 37. At this point it seems assured we will have 61 et al. “eventually”, i.e., given enough terms.
Alternatives.
Alternate Bases 3 and 6.
We have examined ab(n), that is, a base b analog to a(n), considering the sums of base-b digits, using base-b arithmetic, when we examined “digit saturation”. The behavior of these base-b (b ≠ 10) sequences is similar to that of a(n) (i.e., the decimal variety originally considered). We had . Setting these alternatives
If a(1) is set to 3 instead of the least prime 2, we might be able to construe the sequence as a permutation of the primes, if the above conjecture proves true. Instead of reusing a(n), we deem this sequence b(n). The other properties of the sequence (a cloud structure in the plot, computational approaches, etc.) are expected to be largely the same. b(n) begins:
3, 31, 41, 5, 53, 83, 11, 2, 23, 59, 149, 1409, 1423, 101, 29, 113, 503, 89, 17, 809, 173, 1103, 509, 1427, 1429, 163, 103, 43, 7, 71, 811, 107, 821, 1109, 1117, 109, 1009, 1013, 521, 823, 13, 47, 1123, 73, 1019, 1129, 131, 523, 1021, 401, 541, 1031, ...
We observe the production of all four single-decimal-digit primes and overall, similar behavior to a(n). It may be interesting to compare the emergence of primes p in a(n) and in b(n). This paper may be extended to examine b(n) and compare it to a(n).
Table 1b lists the prefix s, the number of instances of s, the first position of s and associated value, and progenitor in both sequences:
s pop m a(m) a(n-1) s pop n b(n) b(n-1)
2 4 1 2 Given 2 3 8 2 11
4 11 15 41 211 4 10 3 41 31
5 33 3 5 23 5 33 4 5 41
7 109 28 7 43 7 109 29 7 43
8 146 5 83 53 8 146 6 83 53
10 331 13 101 1423 10 331 14 101 1423
11 610 6 11 83 11 610 7 11 83
13 1045 40 13 823 13 1045 41 13 823
14 1301 10 149 59 14 1301 11 149 59
16 2202 25 163 1429 16 2202 26 163 1429
17 2919 18 17 89 17 2918 19 17 89
19 4121 65 19 829 19 4121 66 19 829
20 4519 86 2003 839 20 4519 87 2003 839
22 5910 119 223 1759 22 5910 120 223 1759
23 6799 133 233 1787 23 6799 134 233 1787
25 7690 159 251 1789 25 7691 160 251 1789
26 7695 258 263 1979 26 7695 259 263 1979
28 8014 303 281 1999 28 8014 304 281 1999
29 8101 553 293 19289 29 8101 554 293 19289
31 7589 722 31 17599 31 7588 723 311 17599
32 6905 912 3203 17789 32 6905 910 3203 17789
34 5702 966 347 19699 34 5703 964 347 19699
35 5257 1138 353 19889 35 5257 1132 353 19889
37 3822 2832 37 191899 37 3822 2820 37 191899
38 3108 2901 383 191999 38 3108 2901 383 191999
40 2014 5522 4001 194899 40 2014 5521 4001 194899
41 1646 7655 4111 196799 41 1646 7658 4111 196799
43 985 10601 4327 286999 43 985 10601 439 286999
44 658 10713 443 198899 44 658 10694 443 198899
46 338 12095 461 199999 46 338 12104 461 199999
47 237 30954 479 2919899 47 237 30951 479 2919899
49 102 46369 491 2939899 49 102 46379 491 2939899
50 53 46448 50021 2939999 50 53 46453 50021 2939999
52 13 68528 5209 2969899 52 13 68522 5209 2969899
53 11 75712 5303 2978999 53 11 75711 5303 2978999
55 1 92403 5501 2998999 55 1 92403 5501 2998999
56 1 93352 5623 2999999 56 1 93352 5623 2999999
This table demonstrates the similarity of the sequences at least as far as populations of s and their progenitors are concerned. Compare to Table 1.
Table 3b shows the first position m of prime pi , along with progenitor a(m − 1), given the first 100,000 terms of a(n). We know 3 does not occur in a(n), so we place a dash (−) in the third and fourth columns. We compare these to the first position n of prime pi , along with progenitor b(n − 1), given the first 100,000 terms of b(n).
i p_i m a(m) a(m-1) n b(n) b(n-1)
-----------------------------------------------------
1 2 1 2 Given 8 2 11
2 3 . . . 1 3 Given
3 5 3 5 23 4 5 41
4 7 28 7 43 29 7 43
5 11 6 11 83 7 11 83
6 13 40 13 823 41 13 823
7 17 18 17 89 19 17 89
8 19 65 19 829 66 19 829
9 23 2 23 2 9 23 2
10 29 7 29 11 15 29 101
11 31 722 31 17599 2 31 3
12 37 2832 37 191899 2820 37 191899
13 41 15 41 211 3 41 31
14 43 27 43 103 28 43 103
15 47 41 47 13 42 47 13
16 53 4 53 5 5 53 5
17 59 9 59 113 10 59 23
18 61 . . . . . .
19 67 . . . . . .
20 71 29 71 7 30 71 7
21 73 43 73 1123 44 73 1123
22 79 62 79 1033 63 79 1033
23 83 5 83 53 6 83 53
24 89 17 89 503 18 89 503
25 97 . . . . . .
26 101 13 101 1423 14 101 1423
27 103 26 103 163 27 103 163
28 107 31 107 811 32 107 811
29 109 35 109 1117 36 109 1117
30 113 8 113 29 16 113 29
Note that the progenitors of pi are generally the same in both sequences. This may lead us to consider that there may be a way to surmise how these numbers might be efficiently predicted. We know that the list of prefixes s remains small, threading through the one- and two-digit numbers. Therefore it may serve us to identify the smallest prime that exceeds, say, s × (10 s/9 − 1). This may give us a useful reference for the progenitor of 61 in either sequence. Compare to Table 3.
Table 4b: Comparison of first position m of a(m) beginning with digit d, and n of b(n) beginning with same, for sequences with 100,000 terms each:
d m a(m) n b(n)
-----------------------
1 6 11 7 11
2 1 2 8 2
3 722 31 1 3
4 15 41 3 41
5 3 5 4 5
6 . . . .
7 28 7 29 7
8 5 83 6 83
9 . . . .
Compare this to Table 4.
Digital Root vs. Digital Sum.
Let R(n) signify the decimal digital root of n. (Here we concern ourselves only with decimal or base b = 10.) A digital root is simply the number resulting from repeatedly adding the digits of a number again and again till we arrive at a single digit. Thus, for the number 1048576, the sum of digits is 31; the sum of the digits of 31 is 4. So 4 is the digital root of 1048576.
This sequence r(n) has a clearer and less-contested set of lineages or striations, that is, in the case of r(n), the single-digit prefix s.
The digit-sum version a(n) admits multiple decimal digit s, for instance, the prime 4999 → 31 = s, but the digital-root version r(n) requires 4999 → 31 → 4 = s, noting that any further iteration of the latter still results in the fixed point 4.
We know that we cannot have s = R(n) such that 3 | s for the same reason as a(n), namely that decimal numbers m whose sum-of-digits is divisible by 3 are likewise themselves divisible by 3. Thus, we will never see s = 3, 6, or 9, except in the explicit case where R(n) = prime p = 3. We are left then with only 6 possible values of s: 1, 2, 4, 5, 7, or 8. Generalizing to any base b, s is forbidden from any multiple kd such that 1 < d | (b − 1). Therefore, hexadecimally (i.e., for b = 16), we may only have 8 possible values of s; 1, 2, 4, 7, 8, 11, 13, 14.
Therefore, given the constriction of all the action that makes for a(n) to just 6 lineages in the case of r(n), there is much less intercalation of striations apropos to 10e and those to 10(e + 1). These exhaust themselves much more quickly and are more “connected” with the decimal magnitude m of n, i.e., m = log10 n. There are only so many D-digit decimal prime numbers p that begin with 1, 2, 4, 5, 7, or 8. Once we are out of them, the function pops to the next order of magnitude, beginning with the smallest prime greater than d × 10(e + 1).
We then have a plot (Figure 10 below) of a scaling up of six lineages, only seemingly paired, pertaining to r(n) = 1, 2, 4, 5, 7, or 8. The graph is pretty different; it is a simplification of the behavior of a(n), wherein we have six fairly linear striations to a “cloud”.
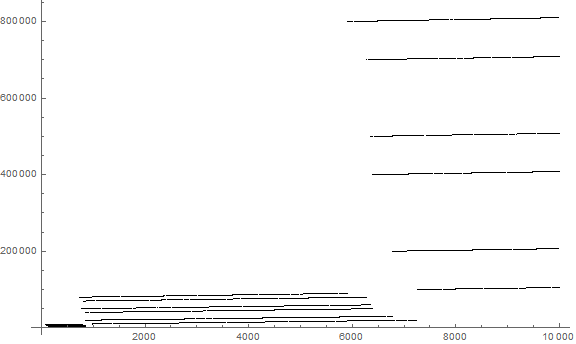
Figure 11 is a log-log plot of r(n):
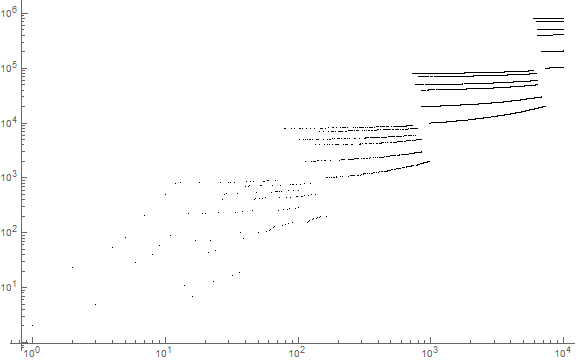
The “clouds” grow ever more distinctly resolved and the lineages with less intercalated delay as the magnitude increases. Like that of a(n), the plot of r(n) doesn’t paint the striations such that they are consecutively constructed line by line, but instead, skips between and among them, even between magnitudes, based on the reserve of d-initial digit primes that occur in the interval. We see the advent of large d primes (i.e., those beginning with 8) for a given magnitude precede those of small d primes (i.e., those beginning with 1). A question: would there be a case where the large-d primes of a given magnitude exhaust before the small-d primes? If so, this would seem possible only for very large n at a threshold that lies perhaps given several dozen or a hundred orders of decimal magnitude.
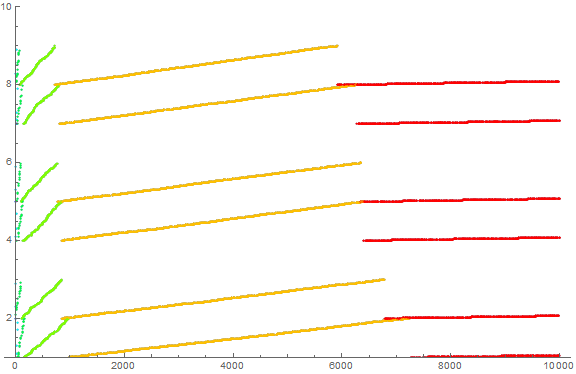
We can align the lineages attributable to s, which in the case of r(n), is rendered very simple in comparison to a(n). Thus, we plot r(n)/ ⌈log10 r(n)⌉ in order to organize the chart in terms of their initial single-digit s. This plot (Figure 12 below) clarifies the modus operanda of the function, showing that indeed there are 6 lineages that exhaust themselves before “graduating” to the next magnitude M. In the plot, we color-code according to M, so that r(n) plotted red has 5, gold 4, green 3, cyan 2, and dark blue 1 decimal digit:
Perhaps more clear is a plot where the x axis (i.e., the index n) is plotted as to log n. This plot (Figure 13 below) allows the smaller n to scale and exhibit the effect of the magnitude of the index on the value of r(n):
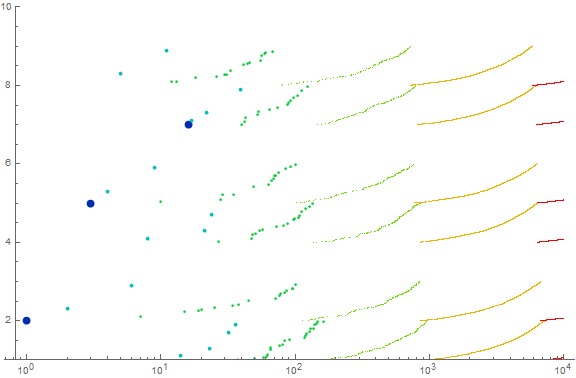
In Figure 13, we see the lineages growing ever fuller and purer, the curves (an artifact of the log-index plot) becoming more “complete” and closer to a pure curve as n increases.
We have allowed the number of decimal digits to govern both the color and size of the points shown in Figure 13. Therefore we can easily pick out the first several dozen terms {2, 23, 5, 53, 83, 29, 211, 41, 59, 503, 89, 809, 811, 11, 223, 7, 71, 821, 227, 229, 43, 73, 13, 47, 233, 823, 401, 509, 521, 827, …}. We note the delayed start of the lineage of 7, something in common r(n) suffers in common with a(n).
Indigo large dots represent single-digit terms 2, 5, and 7 (we are missing 3, since it begins with a forbidden digit). Cyan medium dots represent double-digit terms 23, 53, 83, 29, 41, 59, etc. Dark green small dots represent three-digit terms, etc.
Indeed, looking only at the lineage of one of the six primitive values of s, we see a clear induction on the prime index π(p) for p starting with digit s, constrained by having the first digit s. For instance, for s = 4, there is no prime with 1 digit starting with 4, but we have 41, 43, 47 in cyan, then {401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499}, then {4001, …, 4999}, etc., in this order, again only examining the portion of the plot between 4 ≤ y < 5. Therefore, this sequence is clearly not a permutation of the primes, clearly missing primes that start with 3, 6, or 9 in base ten.
What is missing from the behavior of r(n) vs. a(n) is the burgeoning of two-digit s, then three-digit s, which tends to sweep out across the initial digits 3, 6, and 9 so as to cover them in a(n) as n approaches infinity. Therefore r(n) is definitely not a permutation of the primes. We will never see, for example, primes 31, 37, 61, 67, 97, not to mention larger primes beginning with 3, 6, or 9.
The sequence r(n) lends credence to our analysis of a(n).
We surmise the chart, being markedly simple, would prove similar in other bases so as to render examining them relatively uninteresting.
This concludes our examination of OEIS A337099.
Appendix.
Code 1: Generate A337099 using suffix length j and A045572(k) (twin iterator approach):
Nest[Block[{a = #, d = IntegerDigits[Total@ IntegerDigits[#[[-1]] ] ], k = 0, j = 1, n},
Append[#,
While[Nand[FreeQ[a, #], PrimeQ@ #] &@
Set[n, If[k == 0, FromDigits@ d,
FromDigits[Join[d, PadLeft[IntegerDigits[(5 k + Mod[3 k + 2, 4] - 4)/2], j]]]]],
If[# == j, Set[{j, k}, {# + 1, 1}], k++] &[Log10[k/4]]]; n]] &, {2}, 120]
Code 2: Generate A337099 using iterator memoization approach:
Nest[Block[{a = #, d = IntegerDigits[Total@ IntegerDigits[#[[-1, 1]] ] ], k = 0, j = 1, n},
If[FreeQ[a[[All, 2]], d], Set[{j, k}, {0, 1}],
Set[{j, k}, a[[Position[a[[All, 2]], d][[-1, 1]], -1]]]];
Append[a,
While[Nand[FreeQ[a[[All, 1]], #], PrimeQ@ #] &@
Set[n, If[k == 0, FromDigits@ d,
FromDigits[
Join[d, PadLeft[IntegerDigits[(5 k + Mod[3 k + 2, 4] - 4)/2], j]]]]],
If[# == j, Set[{j, k}, {# + 1, 1}], k++] &[Log10[k/4]]]; {n, d, {j, k}}]] &,
{{2, {2}, {0, 1}}}, 10^5][[All, 1]]
Code 3: Generate A337099 using external prefix memoization approach:
Block[{t},
Nest[Block[{a = #, d = IntegerDigits[Total@IntegerDigits[#[[-1]] ] ], k = 0, j = 1, s, n},
s = FromDigits@ d;
If[ListQ[t[s]], Set[{j, k}, t[s]] ];
Append[#,
While[Nand[FreeQ[a, #], PrimeQ@ #] &@
Set[n, If[k == 0, s,
FromDigits[
Join[d, PadLeft[IntegerDigits[(5 k + Mod[3 k + 2, 4] - 4)/2], j]]]]],
If[# == j, Set[{j, k}, {# + 1, 1}], k++] &[Log10[k/4]]];
Set[t[s], {j, k}]; n]] &, {2}, 10^5] ]
Code 4.1: Generate A337099 using external prefix memoization approach:
Block[{t},
r = r045572[[1 ;; 4*10^Floor@ Log10[nn]]];
Nest[Block[{a = #, d = IntegerDigits[Total@IntegerDigits[#[[-1]] ] ], k = 0, j = 1, s, n},
s = FromDigits@ d;
If[ListQ[t[s]], Set[k, t[s]] ];
Append[#,
While[Nand[FreeQ[a, #], PrimeQ@ #] &@
Set[n, If[k == 0, s, FromDigits@ Join[d, Reverse@ IntegerDigits@ r[[k]] ]]], k++];
Set[t[s], k]; n]] &, {2}, 10^5] ]
Code 4.2: Pre-generate suffixes t in reverse (i.e., the “r045572” in Code 4.1 above):
Flatten@ Table[#*10^(n - IntegerLength@ # + 1) &@
IntegerReverse[(5 k + Mod[3 k + 2, 4] - 4)/2], {n, 0, 6}, {k, 4*10^n}]
Log-Log Plots in Bases 3 and 6.
Figure 10. Base 3, log-log plot of a3(n) for 1 ≤ n ≤ 310 (i.e., 59049).
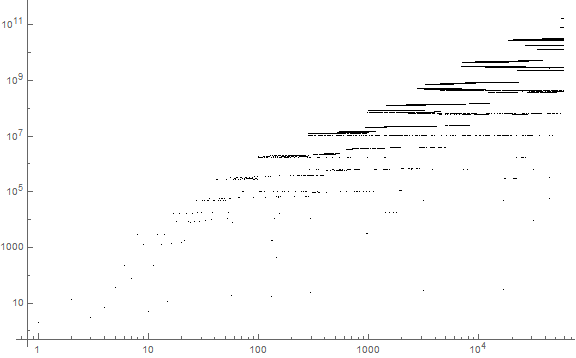
Figure 11: Base 6, log-log plot of a6(n) for 1 ≤ n ≤ 66 (i.e., 46656).
Concerns sequences:
A045572: Odd numbers indivisible by 5.
A054750: Smallest prime number whose digits sum to n-th prime.
A337099: a(n) (see above).
Document Revision Record.
2020 0826 1730 Created.
2020 0827 1930 Conjecture at end.
2020 0828 1200 Figure 3.
2020 0828 1545 Figures 4 & 5.
2020 0829 0915 Extension of a(n) to 100,000 terms, associated observations and tables.
2020 0829 1100 Sequence b(n) to 100,000 terms and associated observations and tables.
2020 0830 0830 Nature of the shape of the clouds, continual increase in terms of a(n) to 300,000.
2020 0830 1515 Figure 7 and description of the nature of the plot of a(n).
2020 0830 1800 Attempted disentanglement of the self-referential nature of a(n).
2020 0902 2215 Studies in bases 3 and 6.
2020 0904 1615
Contents, computation experimentation.
2020 0910 1600 r(n) a digital-root version of a(n), Figures 10-13.