Chains of Nearly Doubled Primes.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2020 1117.
Abstract.
A Cunningham chain is sequence of primes that are each nearly double the preceding prime. Those of the first kind have p → q = 2p + 1, while those of the second kind have p → q = 2p − 1. We define the sequence of Cunningham chains of the first kind, sorted by their least prime as P = OEIS A075712, related to Sophie Germain primes in A5384. The sequence of Cunningham chains of the second kind, sorted by their least prime we note as Q = A338944, related to primes in A5382. P and Q include “singleton chains” and are therefore permutations of the primes.
This paper examines basic properties of two conditional self-referential integer sequences s and t that generate complete Cunningham chains, conceptualized November 2020 by David Sycamore. The first sequence s generates Cunningham chains of the first kind, while the second sequence t produces Cunningham chains of the second kind. These sequences additionally generate the composite number that serves as an upper barrier to the chains.
Introduction.
A Cunningham chain of the first kind is a series of primes pk such that for all 1 ≤ k ≤ ℓ, p(k + 1) = 2 p + 1, while a Cunningham chain of the second kind instead has p(k + 1) = 2 p − 1. A complete Cunningham chain has length ℓ, beginning with p such that (p − 1)/2 or (p + 1)/2 is not prime, respectively, regarding sequence P or Q.
Alternatively, given the first prime in a Cunningham chain p1, we may find all primes pk for all 1 ≤ k ≤ ℓ via:
pk = 2(k − 1)p1 + (2(k − 1) − 1) (1st kind), or
pk = 2(k − 1)p1 − (2(k − 1) − 1) (2nd kind)
The first sequence s begins with s(1) = 1. Thereafter, if s(n) is prime, then s(n + 1) = 2 × s(n) + 1, else s(n + 1) = least prime not already in s(n). The sequence generates Cunningham chains consisting of Sophie Germain primes (OEIS A5384). The first 30 terms of this sequence:
1, 2, 5, 11, 23, 47, 95, 3, 7, 15, 13, 27, 17, 35, 19, 39, 29, 59, 119, 31, 63, 37, 75, 41, 83, 167, 335, 43, 87, 53, 107, ...
We might put these instead in rows:
1;
2, 5, 11, 23, 47, 95;
3, 7, 15;
13, 27;
17, 35;
19, 39;
29, 59, 119;
31, 63;
37, 75;
41, 83, 167, 335;
43, 87;
etc.
We observe in examples in [5] descriptions of the first Cunningham chains of the first and second kinds along with the composite number that terminates them.
The sequence t starts with t(1) = 1. Thereafter, if t(n) is prime, then t(n + 1) = 2 × t(n) − 1, else t(n + 1) = least prime not already in t(n). The sequence generates complete Cunningham chains of primes in OEIS A5382. The first 30 terms of this sequence:
1, 2, 3, 5, 9, 7, 13, 25, 11, 21, 17, 33, 19, 37, 73, 145, 23, 45, 29, 57, 31, 61, 121, 41, 81, 43, 85, 47, 93, 53, 105, ...
This can of course be seen as a series of rows as we have shown regarding s.
Complete Cunningham chains result from these sequences by definition, whereupon we arrive at a composite term, we record it, then reset to the least unused prime in the immediately following term to build the next chain. We are thus assured to generate complete Cunningham chains, delimited by the composite number that terminates the chain.
The extraction of complete Cunningham chains.
We may use the composite numbers in sequence s or t to delimit the Cunningham chains of length ℓ, facilitating the respective sequences of lengths Lp and Lq. The first 30 terms of Lp = A338945:
5, 2, 1, 1, 1, 2, 1, 1, 3, 1, 2, 1, 1, 1, 1, 1, 6, 1, 1, 1, 1, 2, 1, 2, 1, 1, 1, 1, 1, 1, ...
The sequence of least indices of Lp with length ℓ:
3, 2, 9, 79, 1, 17, ...
The first 30 terms of Lq:
3, 2, 1, 1, 3, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 3, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, ...
The sequence of least indices of Lq with length ℓ (with ℓ = 5 not observed for t(n) with 1 < n < 10000):
3, 2, 1, 285, 213, (?), 1766, ...
Therefore, for sequence P, we derive the Cunningham chains of the first kind:
2, 5, 11, 23, 47;
3, 7;
13;
17;
19;
29, 59;
31;
37;
41, 83, 167;
43;
53, 107;
61;
etc.
Thus, the rows constitute the first, second, third, etc. Cunningham chains of the first kind.
Likewise, for sequence Q, we derive the Cunningham chains of the second kind:
2, 3, 5;
7, 13;
11;
17;
19, 37, 73;
29, 59;
23;
29;
31, 61;
41;
etc.
Thus, the rows constitute the first, second, third, etc. Cunningham chains of the second kind.
Table 1, produced from data at [2], shows properties of the first instance of a Cunningham chain of the first kind with length ℓ. The prime p1 is found in the i-th row of P.
ℓ π(p_1) p_1 i
--------------------------------------------
1 6 13 3
2 2 3 2
3 13 41 9
4 97 509 79
5 1 2 1
6 24 89 17
7 87359 1122659
8 1216984 19099919
9 4991062 85864769
10 1137462214 26089808579
11 25401206880 665043081119
12 21334338642 554688278429
13 117161362875266 4090932431513069
...
Table 2, also produced from data at [2], shows properties of the first instance of a Cunningham chain of the second kind with length ℓ:
ℓ π(p_1) p_1 i
-------------------------------------------
1 5 11 3
2 4 7 2
3 1 2 1
4 321 2131 285
5 242 1531 213
6 32731 385591
7 1926 16651 1766
8 1001790 15514861
9 43926857 857095381
10 8219445158 205528443121
11 51603105525 1389122693971
12 6781725101365 216857744866621
13 22813454870490 758083947856951
...
We see that we may be able to ascertain the index i for the least prime p1 of the Cunningham chain of second kind, such that ℓ = 6.
Per [2], we see there should be infinitely many chains of any nonzero positive length ℓ; though in [5] there is a citation of Dickinson’s conjecture et al. supporting this assertion, yet we cannot generate these chains directly. We see in the sequences studied simply too few terms so as to observe very long chains exceeding, say, ℓ = 8. This, despite the fact that P and Q begin with > 1. There are useful remarks in [5] as to the frequency of the occurrence of chains of a particular length ℓ.
Bounding Nonprimes.
Effacing the primes from s, we obtain a series of nonprime numbers that serve as upper barriers for the i-th Cunningham chain of the first kind:
1, 95, 15, 27, 35, 39, 119, 63, 75, 335, 87, 215, 123, 135, 143, 147, 159, 5759, 195, 203, 207, 219, 455, 255, 527, 275, 279, 299, 303, 315, ...
Sorted and ignoring the empty product, we have the sequence st that contains composite numbers that serve as upper barriers for Cunningham chains of the first kind:
15, 27, 35, 39, 63, 75, 87, 95, 119, 123, 135, 143, 147, 159, 195, 203, 207, 215, 219, 255, 275, 279, 299, 303, 315, 327, 335, 363, 387, 395, ...
We can determine the numbers that serve as lower barriers for the i-th Cunningham chain of the first kind. Here we use instead a function f(x) = (x − 1)/2 applied to the least prime p1 of the i-th Cunningham chain of the first kind. This would be the sequence sb, ignoring non-integers:
1, 6, 8, 9, 14, 15, 18, 20, 21, 26, 30, 33, 35, 36, 39, 44, 48, 50, 51, 54, 56, 63, 65, 68, 69, 74, 75, 78, 81, 86, ...
Likewise, we may erase the primes from t to obtain a series of nonprime numbers that serve as upper barriers for the i-th Cunningham chain of the second kind:
1, 9, 25, 21, 33, 145, 45, 57, 121, 81, 85, 93, 105, 117, 133, 141, 625, 165, 177, 385, 201, 205, 213, 217, 225, 253, 261, 273, 553, 297, ...
Sorted and ignoring 1, we have the sequence tt that contains composite numbers that serve as upper barriers for Cunningham chains of the second kind:
9, 21, 25, 33, 45, 57, 81, 85, 93, 105, 117, 121, 133, 141, 145, 165, 177, 201, 205, 213, 217, 225, 253, 261, 273, 297, 301, 325, 333, 345, ...
We can determine the numbers that serve as lower barriers for the i-th Cunningham chain of the second kind. Here we use instead a function g(x) = (x + 1)/2 applied to the least prime p1 of the i-th Cunningham chain of the second kind. This would be the sequence tb, ignoring non-integers:
4, 6, 9, 10, 12, 15, 16, 21, 22, 24, 27, 30, 34, 36, 40, 42, 45, 49, 51, 52, 54, 55, 57, 64, 66, 69, 70, 75, 76, 82, ...
We may find interest in looking for certain classes of composites among these barrier numbers, such as perfect powers of 2 or squares, etc.
Plots.
Figure 1 is a plot of s(n) for 1 < n < 120, showing Sophie Germain primes called out, in large yellow dots, otherwise red for primes and blue for nonprimes:
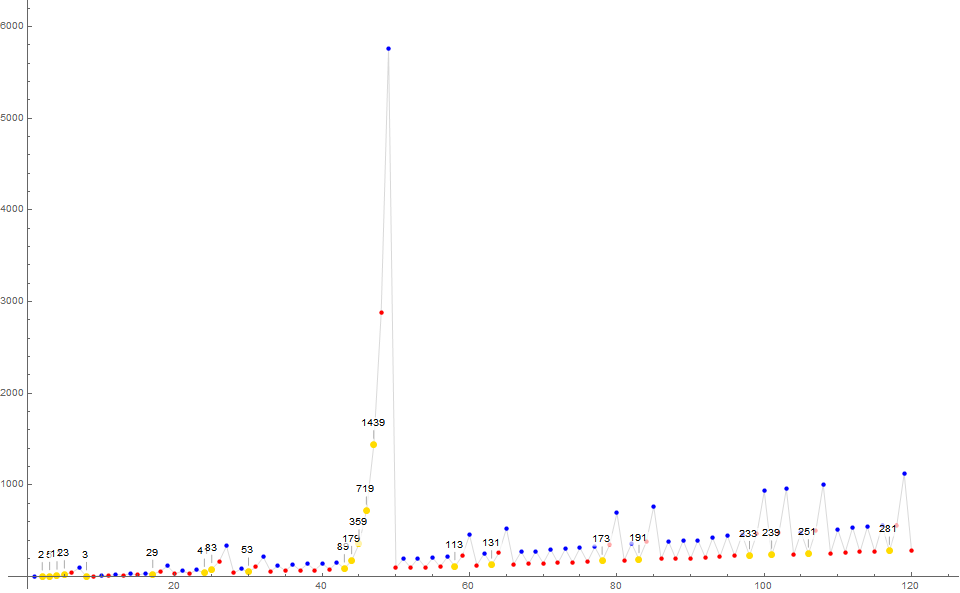
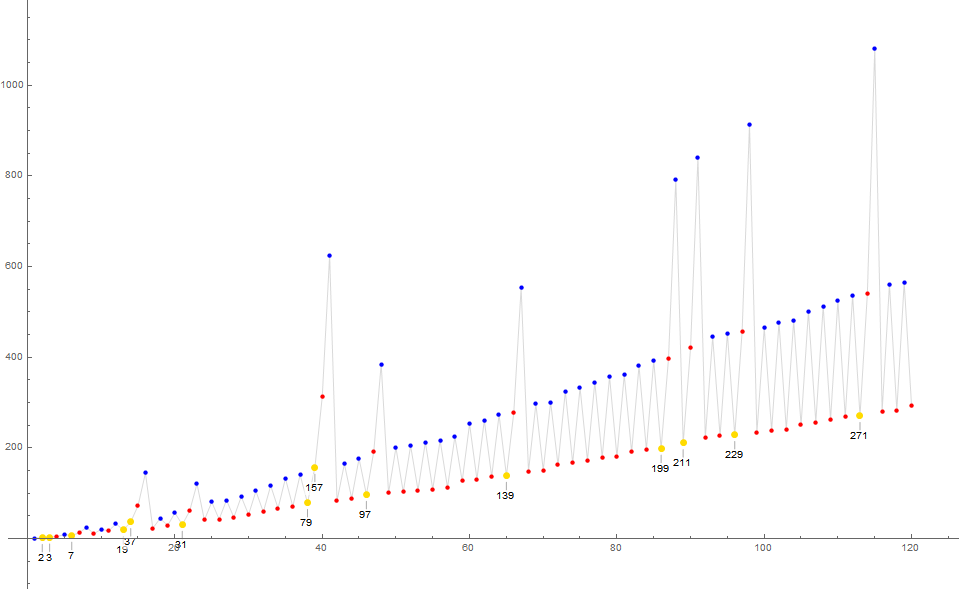
Figure 2 is a plot of t(n) for 1 < n < 120, showing primes in A5382 called out, in large yellow dots, otherwise red for primes and blue for nonprimes:
This concludes our examination of Cunningham chains.
Appendix:
Code 1: Generate P(n) = A075712(n):
Block[{a = {2}, k, p},
Do[k = 1; If[PrimeQ@ a[[-1]],
AppendTo[a, 2 a[[-1]] + 1],
While[! FreeQ[a, Set[p, Prime[k]]], k++];
Set[a, Append[a[[1 ;; -2]], p]]], {i, Length@ a + 1, 10^3}]; a]
Code 2: Generate Q(n) = A338944(n):
Block[{a = {2}, k, p},
Do[k = 1; If[PrimeQ@ a[[-1]],
AppendTo[a, 2 a[[-1]] + 1],
While[! FreeQ[a, Set[p, Prime[k]]], k++];
Set[a, Append[a[[1 ;; -2]], p]]], {i, Length@ a + 1, 10^3}]; a]
Code 3: Generate Lp(n) = A338945(n):
Block[{a = {2}, b = {}, j = 0, k, p},
Do[k = Length@ b + 1; If[PrimeQ@ a[[-1]],
AppendTo[a, 2 a[[-1]] + 1]; j++,
While[! FreeQ[a, Set[p, Prime[k]]], k++]; AppendTo[b, j];
Set[j, 0]; Set[a, Append[a[[1 ;; -2]], p]]], {i, Length@ a + 1, 1500}]; b]
Code 4: Generate Lq(n) = A338946(n):
Block[{a = {2}, b = {}, j = 0, k, p},
Do[k = Length@ b + 1; If[PrimeQ@ a[[-1]],
AppendTo[a, 2 a[[-1]] - 1]; j++,
While[! FreeQ[a, Set[p, Prime[k]]], k++]; AppendTo[b, j];
Set[j, 0]; Set[a, Append[a[[1 ;; -2]], p]]], {i, Length@ a + 1, 1500}]; b]
Block[{a = {1}, k, p},
Do[k = 1; If[PrimeQ@ a[[-1]],
AppendTo[a, 2 a[[-1]] + 1],
While[! FreeQ[a, Set[p, Prime[k]]], k++]; AppendTo[a, p]], 10^3]; a]
Block[{a = {1}, k, p},
Do[k = 1; If[PrimeQ@ a[[-1]],
AppendTo[a, 2 a[[-1]] - 1],
While[! FreeQ[a, Set[p, Prime[k]]], k++]; AppendTo[a, p]], 10^3]; a]
References:
[1] Dirk Augustin, Cunningham Chain records.
[2] Chris K. Caldwell, Cunningham Chains, Prime Glossary, PrimePages.
[3] Chris K. Caldwell, Cunningham Chains (1nd kind), PrimePages Top 20.
[4] Chris K. Caldwell, Cunningham Chains (2nd kind), PrimePages Top 20.
[5] Wikipedia, Cunningham chain.
Concerns OEIS sequences:
A005382 Primes p such that 2p − 1 is also prime.
A005384 Primes p such that 2p + 1 is also prime (Sophie Germain primes).
A075712 Rearrangement of primes into Germain groups (i.e., complete Cunningham chains of the second kind, sorted by first prime in the chain).
A338944 Rearrangement of primes into complete Cunningham chains of the second kind, sorted by first prime in the chain.
A338945 Lengths of Cunningham chains of the first kind that are sorted by first prime in the chain.
A338946 Lengths of Cunningham chains of the second kind that are sorted by first prime in the chain.
Document Revision Record.
2020 1117 1800 Created.