The Relay Race Sequence.
A sequence of Brian Beard, posed 5 February 2021.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0205.
Abstract.
This brief examines the behavior of a conditional self-referential recently drafted sequence OEIS A341130 as seen in the plot of the function.
Introduction.
Recall that 1, the empty product, is neither prime nor composite, and that if we have a number m > 1 with two divisors (i.e., the trivial divisors 1 and m itself) we call it prime, else it is composite. Let us refer to the status of a number m being prime or not using the term “primality”.
Let a(n) = n for 1 ≤ n ≤ 2. Thereafter, if a(n−1) and a(n−2) are of the same state of primality, then a(n) = | a(n−1) − a(n−2) |, else a(n) = a(n−1) + a(n−2).
The sequence begins:
1, 2, 3, 1, 4, 5, 9, 14, 5, 19, 14, 33, 19, 52, 71, 123, 194, 71, 265, 336, 71, 407, 478, 71, 549, 620, 71, 691, 620, 1311, 691, 2002, 2693, 4695, 7388, 2693, 4695, 7388, 2693, 10081, 12774, 2693, 15467, 12774, 28241, 15467, 43708, 59175, 15467, 74642, 90109, 15467, 105576, 121043, ...
Code 1 generates the sequence. Click here for a text file containing 216 + 2 terms.
a(3) = 3 since 1 and 2 have dissimilar primality, hence 1 + 2 = 3.
a(4) = 1 since 2 and 3 are both prime, hence | 2 − 3 | = 1.
a(5) = 4 since 3 and 1 have dissimilar primality, hence 3 + 1 = 4.
a(6) = 5 since 1 and 4 have dissimilar primality, so 1 + 4 = 5.
a(7) = 9 because 4 is composite but 5 is prime, so 4 + 5 = 9.
a(8) = 14 since 5 and 9 have dissimilar primality, hence 5 + 9 = 14.
a(9) = 5 since 9 and 14 are both composite, therefore | 9 − 14 | = 5, etc.
Figure 1 is a log plot of a(n) for 1 ≤ n ≤ 28, showing nonprimes in blue and primes in red (Click for an extended log plot of a(n) for 1 ≤ n ≤ 212 or an even more extended plot for 1 ≤ n ≤ 216):
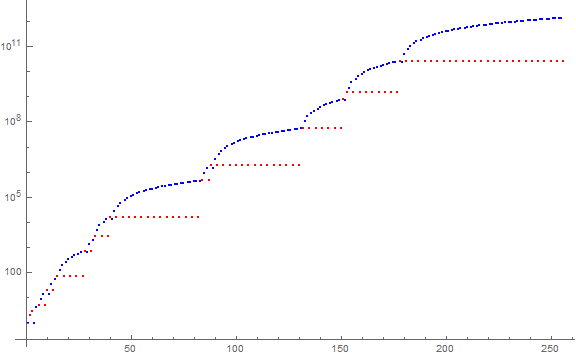
We note a curious repetition of primes in this sequence, or rather, that there are some “singleton” primes q that only appear once, while most primes p appear multiple times, that is, every third term upon first appearing. Given 216 terms m in a(n), there are 4 distinct primes q: {2, 3, 760228181, 4410782411489292213567920279417}, of 135 distinct primes in all (listed here). The primes hold a plateau until a necessarily dissimilar, larger prime appears in the interposing escalation. The larger prime thus takes over and may repeat. There doesn't seem to be a reason why we cannot have additional q, as q' arises the first time we have m + q = q', but only sustains for a single cycle.
The records for repetition are:
1, 2, 5, 15, 38, 41, 66, 84, 86, 229, 262, 313, 457, 601, 769, 810, 882, ...
The indices of these records in sequence a are the following, respectively:
2, 6, 15, 40, 178, 351, 670, 1140, 1422, 2995, 5484, 8506, 14482, 17472, 22204, 26706, 41401, ...
These are set by the primes:
2, 5, 71, 15467, 25628197501, 417526936971769, 23527909757857985943851, 26256320042062297940727797057, 1002533887734553211238539215857293, 33893917858094858717598054976100088751264704982634455397, ...
Additionally, we see that 1 is repeated, as are any composite appearing after two necessarily dissimilar primes. The duplicated nonprimes are:
1, 14, 620, 12774, 1368484, 705795468, 24162173852, 9705756734634, 33808029860992228, 20081633774728459090, 22056100427251978417408, 276251364895133826212564270, ...
The sequence progresses in cycles that feature two nonprimes separating instances of the same or dissimilar primes. Suppose p is a prime that is repeated a number of times, and we have a series of composites c that have the difference p. Now suppose the number q following an instance of p happens also to be prime. The ensuing term m' = | p − q |, which is the number c that preceded p. Now given that q and c have dissimilar primality, we have the next term the sum q + c, and we are starting a new cycle where the increment is q. Suppose c is the first and composite term following a prime p, but q is the second. Since q and c have dissimilar primality, we have the sum q and c and do not have a repeated composite. Instead, the prime p “passes the baton” to q without a repeated c, and we continue with the increment q.
Finally, we examine the case of a singleton prime, using a(151) = 760228181 as an example. We list the terms a(n) with n preceding the term, and the designation “C” if composite and “P” if prime:
145 542497329 C
146 596930042 C
147 54432713 P
148 651362755 C
149 705795468 C
150 54432713 P
151 760228181 P
152 705795468 C
153 1466023649 P
154 2171819117 C
155 3637842766 C
156 1466023649 P
...
Here, the prime p = 54432713 is the increment, and immediately following its seventh repetition in the sequence, we strike a prime q = 760228181. Thus we return to the previous composite c = 705795468, commencing iteration using the step q = 760228181. 705795468 + 760228181 = 1466023649, a third prime number r. Thus, we have no further occurrences of q in the sequence, as r is the new step value, going on to occur 9 times in the sequence.
We observe a relatively regular exponentially spaced occasion of prime plateaus as n increases. This appears to be a manifestation of the general abatement of the commonness of primes at a given magnitude.
This “relay sequence” is like a relay racing team passing the baton, only that the “runners”, which, outside of the very first, are primes p, taking great big strides that are p units long. Therefore the “race” gets ridiculously “fast” as we proceed further into the sequence.
This concludes our examination.
Appendix:
General note: visit the index for other briefs covering OEIS sequences.
Table A: distinct primes p that appear in a(n) for 1 ≤ n ≤ 216. The prime p appears k times in a(n), first at a(n1) and last at a(n2). Because p becomes large as i increases, we use log(p) where log is the natural logarithm. Here, we make no distinction between repeated p and singleton q. See this text file for a list of the smallest 135 distinct primes p in a(n). Here we leave out the 135th prime because its run was yet ongoing when the program reached 216 terms.
i p log(p) k n_1 n_2
--------------------------------------------------
1 2 0.693147 1 2
2 3 1.09861 1 3
3 5 1.60944 2 6 9
4 19 2.94444 2 10 13
5 71 4.26268 5 15 27
6 691 6.53814 2 28 31
7 2693 7.89841 3 33 39
8 15467 9.64646 15 40 82
9 461317 13.0418 2 84 87
10 1829801 14.4197 15 88 130
11 54432713 17.8125 7 132 150
12 760228181 20.4491 1 151
13 1466023649 21.1058 9 153 177
14 25628197501 23.967 38 178 289
15 28.2969 3 291 297
16 30.0865 18 298 349
17 33.6654 41 351 471
18 38.0717 14 472 511
19 41.4035 11 513 543
20 44.4929 35 544 646
21 48.7408 8 648 669
22 51.5125 66 670 865
23 56.3948 45 867 999
24 60.8945 47 1000 1138
25 65.4377 84 1140 1389
26 70.5616 1 1390
27 71.2518 6 1392 1407
28 73.694 5 1408 1420
29 75.9878 86 1422 1677
30 81.1347 2 1678 1681
31 82.5196 26 1683 1758
32 86.466 6 1759 1774
33 88.9493 7 1776 1794
34 91.5824 67 1795 1993
35 96.4797 54 1995 2154
36 101.162 23 2155 2221
37 104.99 72 2223 2436
38 109.96 45 2437 2569
39 114.46 72 2571 2784
40 119.429 46 2785 2920
41 123.951 25 2922 2994
42 127.863 229 2995 3679
43 133.99 210 3681 4308
44 140.03 95 4309 4591
45 145.277 39 4593 4707
46 149.634 39 4708 4822
47 153.99 161 4824 5304
48 159.765 60 5305 5482
49 164.552 262 5484 6267
50 170.814 45 6268 6400
51 175.313 192 6402 6975
52 181.264 157 6976 7444
53 187.013 3 7446 7452
54 188.805 129 7453 7837
55 194.357 223 7839 8505
56 200.457 313 8506 9442
57 206.897 34 9444 9543
58 211.116 162 9544 10027
59 216.897 168 10029 10530
60 222.714 21 10531 10591
61 226.451 23 10593 10659
62 230.28 309 10660 11584
63 236.706 28 11586 11667
64 240.731 168 11668 12169
65 246.548 65 12171 12363
66 251.416 2 12364 12367
67 252.8 78 12369 12600
68 257.849 210 12601 13228
69 263.889 128 13230 13611
70 269.434 39 13612 13726
71 273.791 24 13728 13797
72 277.662 90 13798 14065
73 282.854 139 14067 14481
74 288.482 457 14482 15850
75 295.3 15 15852 15894
76 298.701 185 15895 16447
77 304.614 219 16449 17103
78 310.697 60 17104 17281
79 315.484 36 17283 17388
80 319.761 28 17389 17470
81 323.786 601 17472 19272
82 330.877 34 19273 19372
83 335.097 241 19374 20094
84 341.275 3 20095 20101
85 343.066 291 20103 20973
86 349.432 204 20974 21583
87 355.444 207 21585 22203
88 361.47 769 22204 24508
89 368.808 237 24510 25218
90 374.969 225 25219 25891
91 381.078 147 25893 26331
92 386.762 125 26332 26704
93 392.283 810 26706 29133
94 399.673 273 29134 29950
95 405.976 108 29952 30273
96 411.351 28 30274 30355
97 415.377 58 30357 30528
98 420.13 207 30529 31147
99 426.156 21 31149 31209
100 429.893 219 31210 31864
101 435.976 104 31866 32175
102 441.313 276 32176 33001
103 447.627 3 33003 33009
104 449.418 140 33010 33427
105 455.052 95 33429 33711
106 460.299 348 33712 34753
107 466.845 675 34755 36777
108 474.053 591 36778 38548
109 481.128 478 38550 39981
110 487.99 291 39982 40852
111 494.357 183 40854 41400
112 500.259 882 41401 44044
113 507.735 390 44046 45213
114 514.394 420 45214 46471
115 521.127 260 46473 47250
116 527.381 54 47251 47410
117 532.063 769 47412 49716
118 539.402 150 49717 50164
119 545.105 239 50166 50880
120 551.275 246 50881 51616
121 557.473 96 51618 51903
122 562.731 132 51904 52297
123 568.307 51 52299 52449
124 572.932 261 52450 53230
125 579.189 79 53232 53466
126 584.252 625 53467 55339
127 591.383 163 55341 55827
128 597.17 642 55828 57751
129 604.328 135 57753 58155
130 609.926 3 58156 58162
131 611.717 50 58164 58311
132 616.321 561 58312 59992
133 623.343 750 59994 62241
134 630.657 285 62242 63094
...
Block[{a = {1, 2}},
Do[AppendTo[a,
Which[MemberQ[{##}, 1], Abs[#1 + #2],
SameQ @@ PrimeQ[{##}], Abs[#1 - #2],
True, Abs[#1 + #2]]] & @@ a[[-2 ;; -1]], {i, 2^16}]; a]
Code 2: Plot a(n) in the style of Figure 1:
Block[{nn = 2^16, s = {}, t = {}, out = -100},
Do[If[PrimeQ[#],
AppendTo[s, out]; AppendTo[t, #],
AppendTo[t, out]; AppendTo[s, #]] &@ ss[[i]], {i, nn}];
ListPlot[{s, t}, ImageSize -> 1920, ScalingFunctions -> "Log",
PlotStyle -> {Directive[Blue, PointSize[Small]],
Directive[Red, PointSize[Small]]},
PlotRange -> {{1, nn}, {1, Max@ ss[[1 ;; nn]]}}]]
Concerns OEIS sequences:
A341130 a(n).
Document Revision Record.
2021 0205 2200 Created.
2021 0205 1945 Final.