OEIS A342616.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0316.
Introduction.
We examine a self-referential sequence A342616 = a that employs an internal divisor counting function, defined as follows:
Let m be a distinct or primitive term in a.
a(1) = 1; a(n+1) = Σ_{d | a(n)} cd, where cd is the number of instances of d | a(k) for 1 ≤ k ≤ n.
The sequence a begins:
1, 1, 2, 4, 7, 6, 11, 8, 15, 13, 11, 13, 14, 21, 21, 25, 19, 18, 33, 29, 21, 36, 49, 30, 52, 43, 27, 41, 29, 31, 31, 33, 49, 42, 76, 55, 46, 51, 53, 40, 70, 78, 85, 53, 46, 65, 60, 116, 79, 50, 87, 72, 123, 74, 77, 72, 140, 132, 143, 74, 89, 62, 92, 110, 125, 82, ...
a(2) = 1 since we have 1 instance of 1 | a(k) for 1 ≤ k ≤ n (which we shall abbreviate hereinafter as a count 1(1)).
a(3) = 2 since we have 2(1).
a(4) = 4 since we have 3(1) and 1(2).
a(5) = 7 since we have 4(1), 2(2), and 1(4).
a(6) = 6 since we have 5(1) and 1(7).
a(7) = 11 since we have 6(1), 3(2), 1(3), and 1(6); 6+3+1+1 = 11.
etc.
Clearly, for all n, we have c1 = n − 1 since 1 divides n > 0.
The counter cp for p prime does not set until novel p results from the sum of previous divisor-counts or p | a(n). Therefore there are two methods for p to appear. An example of the first, explicit method is a(3) = 2, arising from Σ_{d | a(n)} cd. The second method first emerges with a(6) = 6, since 3 | 6 and d = 3 has never appeared until then, p = 3 arises indirectly.
For a(n) = p novel, a(n+1) = n, since we have (n − 1)(1) and 1(p). Subsequent appearances of p have a(n+1) exceed n. Primes may appear more than once.
Table 1 shows the first occurrence of a prime p repeated j times:
p n
-------------------------------------------------
2 3
13 4, 6
239 19, 28, 32
3347 325, 380, 426, 466
14033 931, 949, 1092, 1162, 1553
442019 14885, 23247, 25450, 26930, 30506, 36083
...
The two instances of 1 that begin the sequence yield a(3) = 2. The terms a(2) and a(3) are the only instances of a(n) < n. This is because the only register charged with instances is c1 for those terms, and in all other terms, we have the instigator a(n) > 1. Indeed, 1 can never again arise, because the only way we have Σ_{d | a(n)} cd = 1 is when novel a(n) has 1 divisor (1). Clearly 1 has already appeared twice for n ≥ 2. No other number has 1 divisor, therefore we have seen the only occasions of 1.
Generally, we will no longer see m in a(n) for n > m. This implies the lower bound a(n) = n with n > 3. We have shown that a(n) = n results from certain prime a(n − 1).
Records are as follows:
1, 2, 4, 7, 11, 15, 21, 25, 33, 36, 49, 52, 76, 78, 85, 116, 123, 140, 143, 166, 174, 239, 282, 305, 350, ...
These appear at indices:
1, 3, 4, 5, 7, 9, 14, 16, 19, 22, 23, 25, 35, 42, 43, 48, 53, 57, 59, 71, 78, 83, 93, 98, 118, ...
These records are instigated by fairly highly divisible numbers:
1, 2, 4, 6, 8, 14, 21, 18, 21, 36, 30, 42, 70, 78, 60, 72, 72, 132, 96, 160, 168, 180, 120, 300, 276, 330, 450, 280, 180, 504, 240, 420, 528, 756, 336, 780, 780, 420, 720, 1440, 936, 780, 630, 924, 1584, 660, 1200, 1560, 2280, 1200, 2100, 1800, 1260, 1260, 2772, 2400, 1980, 3150, 1560, 3276, 1680, 5280, 2880, 4368, 4032, 2940, 3960, 4620, 4620, 3960, 4560, 2940, 3060, 3240, 6000, 4800, 4500, 3960, 6720, 3780, 6480, ...
Among 260 records in 220 terms of a, the only odd instigators of records are 1 and 21.
David Sycamore offers the following formula:
If a(n) is a prime power pe for some prime p and multiplicity e ≥ 1 then the (only) divisors of a(n) are {pe, p(e − 1), …, p², p, 1}, thus τ(a(n))= e + 1.
Now to compute a(n+1) we need to add (n − 1) to account for the fact that all prior terms are divisible by 1, and there are (n − 1) of them; we already accounted for 1 | pe. Then we have to add 1 for each of the r terms occurring prior to a(n), which are divisible by p (even though p itself might not have appeared in a — and might never appear in the sequence). Therefore:
a(n+1) = (e + 1) + (n − 1) + r = n + e + r.
By the above derivation the formula holds even if prime p has been seen before (alone, as a factor of other prior terms or in some other powers).
Figure 1 is an annotated scatterplot of a(n) for 1 ≤ n ≤ 64 showing records in red and local minima in blue, the latter the occasion of a(n) = n for n > 3.
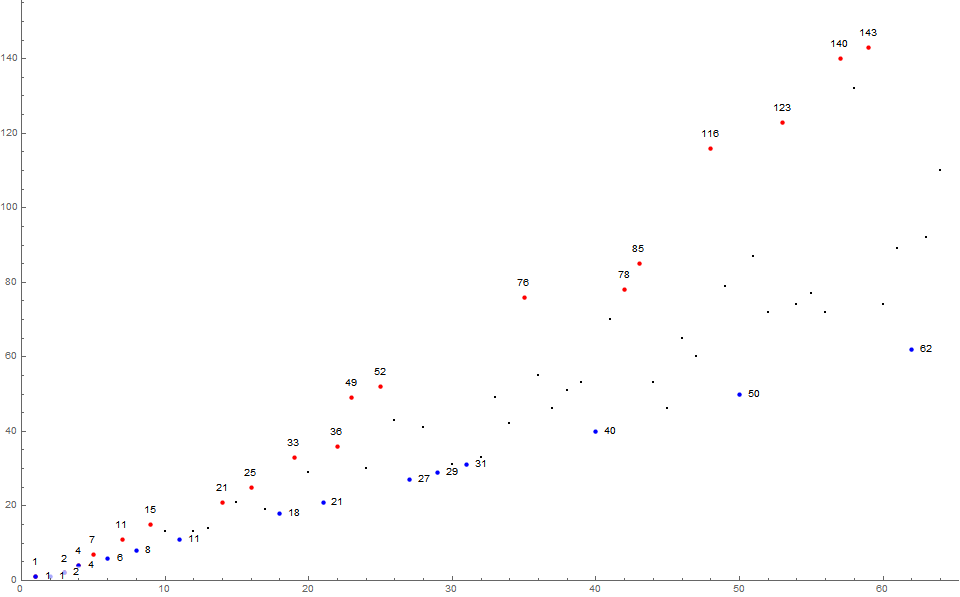
Figure 2 is a scatterplot of a(n) for 1 ≤ n ≤ 216. Click here for an enlarged plot to 220 terms.
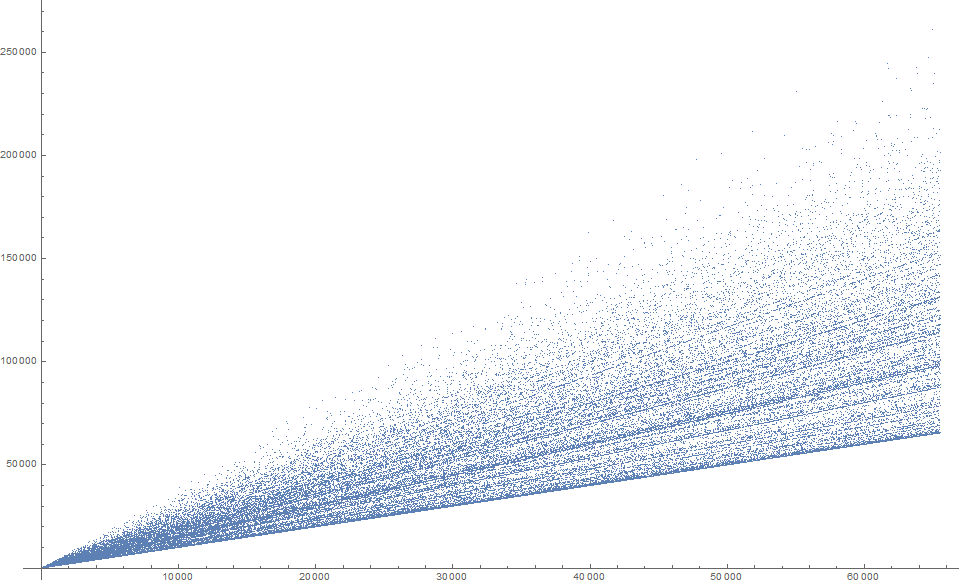
Figure 2 exhibits a fan-like quasi-radial striation pattern akin to the “paint-sprayer” sequence OEIS A279818.
Figure 3 is a scatterplot of a(n) for 1 ≤ n ≤ 4096. The color code applies to the instigator m → a(n), i.e., the progenitor a(n − 1). If m is prime, we color it red. If m is odd and composite, we color it yellow. If m is even we color it blue (except for m = 2, which is colored red).
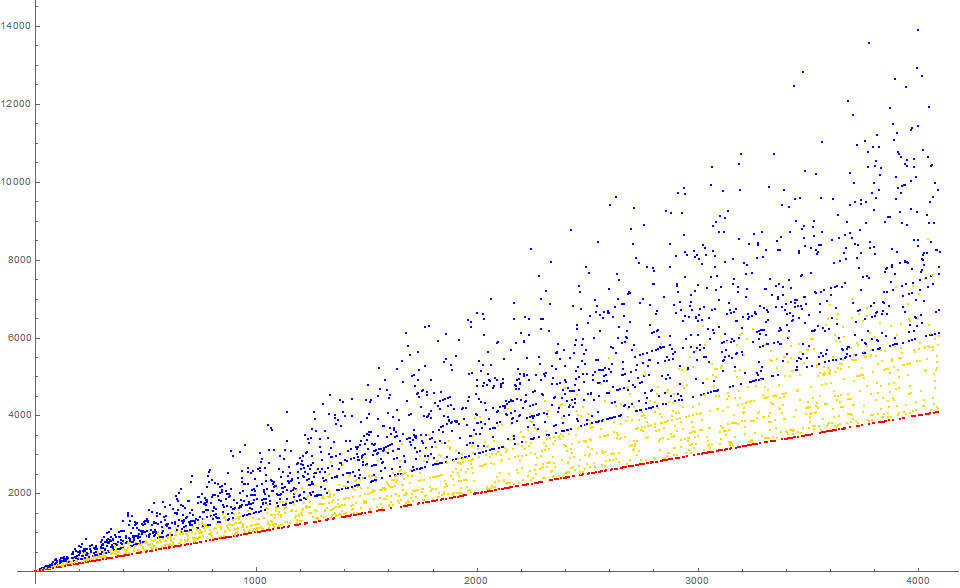
The prime m instigate a(n) that appears along the lowest striation at a(n) = n, comprising the lower bound for n > 3. We also identify a lower bound approximating slope 3/2 for certain a(n) associated with even squarefree semiprime m.
The odd m instigate lower values of a(n) while even m instigate higher values of a(n).
Figure 4 is a scatterplot of a(n) for 1 ≤ n ≤ 4096. The color code applies to τ(m), the number of divisors of m that instigate a(n), with red signifying a low τ(m) (generally, τ(m) = 2) and blue and violet signifying the highest τ(m).
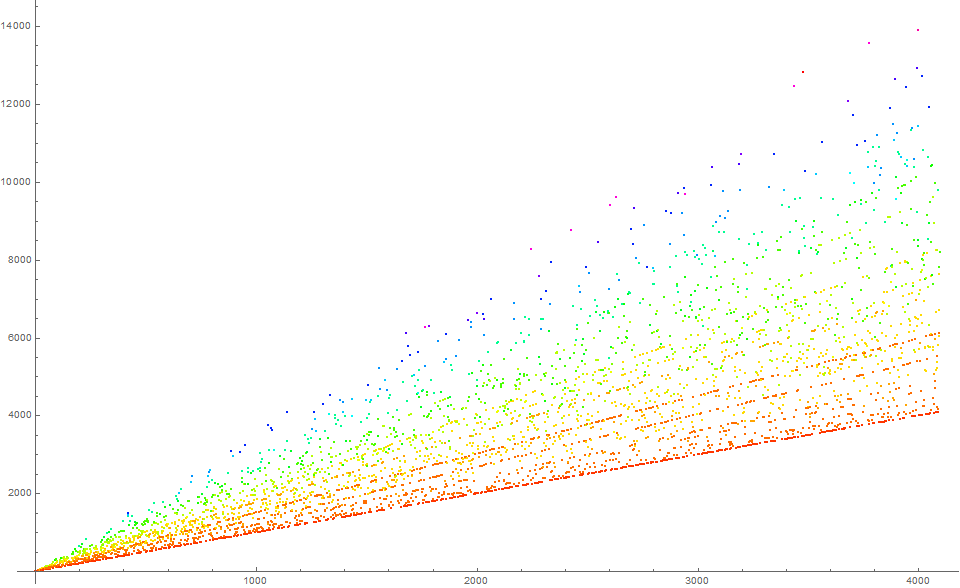
The quasi-radial striations appear to be associated with τ(m). However, we see some “elevated” radials a(k) that occur above a(n) with τ(a(k − 1)) < τ(a(n − 1)). This suggests the cause of the striations is not fully ascertained merely by examination of τ(m).
Figure 5 is a scatterplot of a(n) for 1 ≤ n ≤ 4096. There are some annotations that show the index i in A025487 for A046523(m). The color code applies to i.
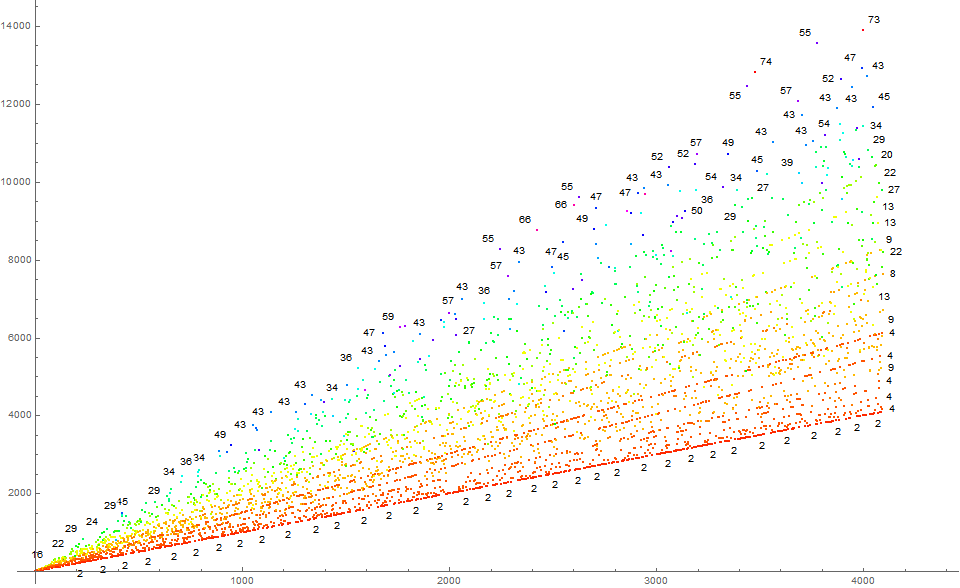
Figure 5 attempts to identify the prime signature of m to pin down the reason for the striations. Of course, this is essentially tantamount to Figure 4.
Figure 6 is a scatterplot of a(n) for 1 ≤ n ≤ 4096 highlighting squarefree semiprime m (with i = 4), color coding them according to least prime factor. Red indicates lpf(m) = 2, orange lpf(m) = 3, etc.
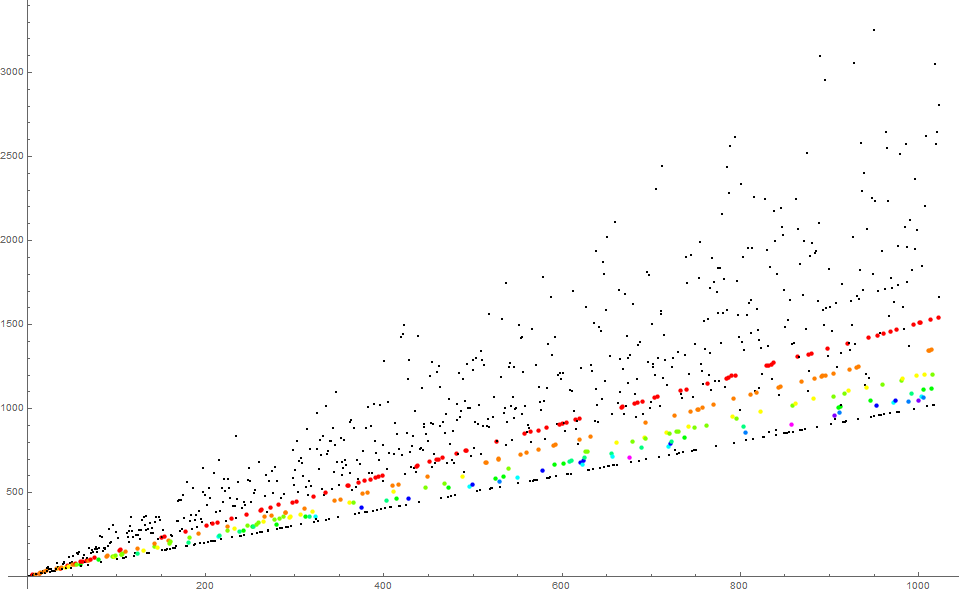
Figure 6 demonstrates that m with the same prime signature are separated by p = lpf(m), with the smallest primes p occuring generally higher as n increases. We see that p = 3 entered the sequence later than 7, therefore, by dint of the frequency of p | a(k), we should see separation according to the magnitude of the prime p, with the least prime appearing above greater primes.
This large-scale log-log scatterplot seems to illustrate that the “radials” are exponential curves.
Figure 7 is a scatterplot of a(n) for 1 ≤ n ≤ 4096 highlighting squarefree semiprime m (with i = 4), color coding them according to greatest prime factor.
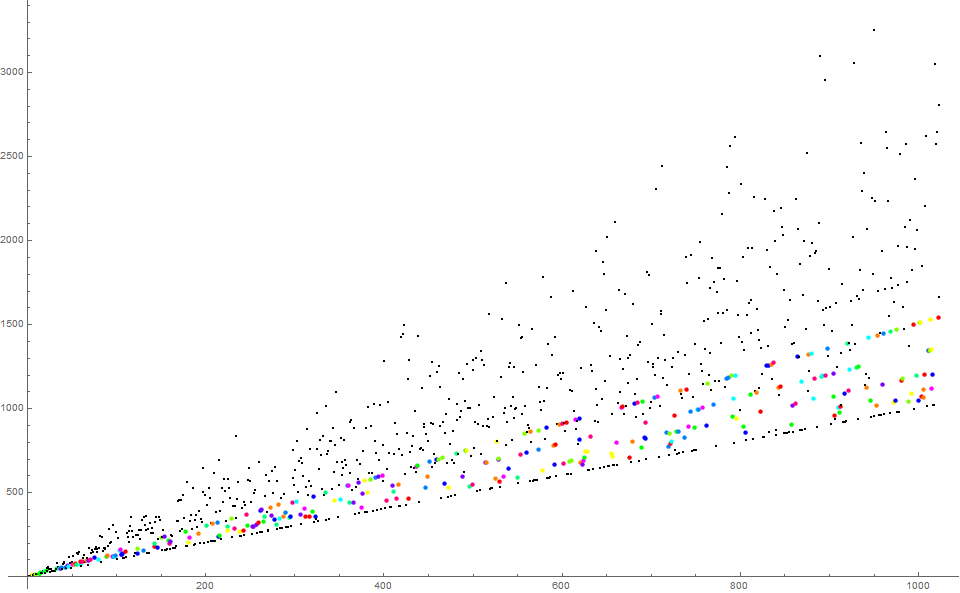There doesn’t appear to be a pattern associated with gpf(m).
Figure 8 is an annotated plot of the incrementation of counters cd for 1 ≤ n ≤ 47. We show an oval in column n whenever d | a(n). The red ovals show when cd increments at n such that a(n) = d. Click here for an enlarged plot showing cd for 1 ≤ n ≤ 960.
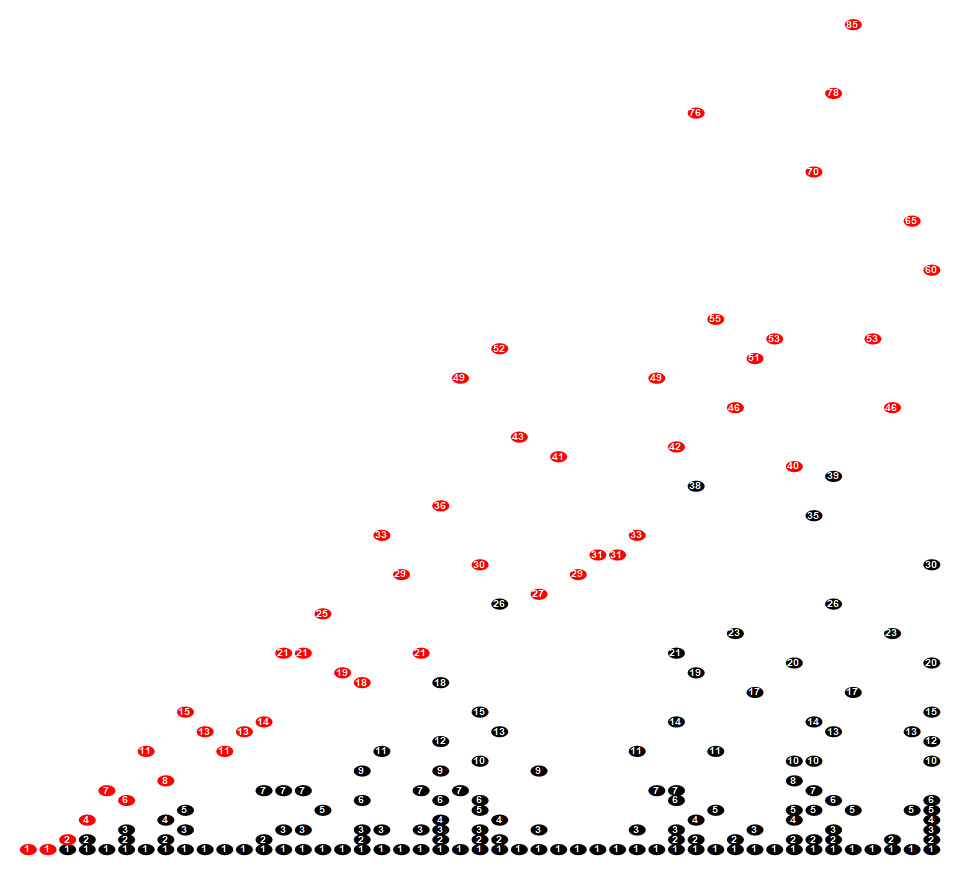
Investigation of the full array of the quasi-radial striations has not been carried out. A study of the frequencies related to various prime factors has not been conducted.
The sequence poses interest because of the quasi-radial striations that relate to the divisor counting function.
This concludes our examination.
Appendix:
Block[{a = {1}, c},
Do[(Map[If[! IntegerQ[c[#] ], Set[c[#], 1], c[#]++] &, #];
AppendTo[a, Total[Map[c[#] &, #]] ]) &@
Divisors[a[[-1]] ], 120]; a]
Concerns OEIS sequences:
A000005: Divisor counting function τ(n).
A025487: Products of primorials; numbers that are the least instance of a given prime signature.
A027750: Row n contains the divisors d | n.
A046523: Numbers m that are the least number of the same prime signature as n.
A279818: a(1) = 1; a(n+1) = sum of digits of a(n), plus sum of same digits arising in all prior terms.
A342616: a(1) = 1; a(n+1) = Σ_{d | a(n)} cd, where cd is the number of instances of d | a(k) for 1 ≤ k < n..
Document Revision Record.
2021 0316 2230.
2021 0317 1330 Figures 8 and extended datasets.
2021 0323 2045 Added Sycamore’s formula.