The Once-and-Nevermore Sequence.
A sequence of David Sycamore.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0502.
Introduction.
We examine a conditional self-referential sequence a = OEIS A343887 that reports the number of terms in a that exceed a new last term m, otherwise it sums the previous term and a least term u already in a thereafter banning such u from being applied again.
Let a(1) = 1; If a(n) is novel, then a(n+1) = the number of a(k) > a(n) for 1 ≤ k < n, else a(n+1) = a(n) + u, a least term a(k) that, once it is used, must be discarded not to be used again.
We define s as a sorted list of terms in a such that s(1) = u; we drop s(1) after deployment in the “extant” condition, with the understanding that the index of s always starts with 1, to maintain s(1) = u. Therefore, the length ℓs increments when the “novel” condition occurs, but remains the same when the “extant” condition plays. In this way, ℓs(n) also represents the number of distinct terms m in a(1..n).
The sequence a begins:
1, 0, 1, 1, 2, 0, 1, 1, 2, 3, 0, 1, 1, 2, 3, 5, 0, 2, 2, 4, 1, 3, 4, 6, 0, 3, 3, 6, 9, 0, 3, 3, 6, 9, 12, 0, 4, 4, 8, 3, 7, 4, 7, 11, 1, 5, 6, 11, 16, 0, 6, 6, 12, 18, 0, 6, 6, 12, 18, 24, 0, 6, 6, 12, 18, 25, 0, 7, 7, 14, 6, 13, 7, 13, 20, 2, 10, 16, 18, 27, 0, 9, 9, 18, 27, 37, 0, 11, 11, 22, 5, 16, 21, 6, 17, 13, 19, 8, 20, 28, 1, 13, 14, 26, 4, 16, 20, 33, 1, 14, 15, 24, 37, 50, 0, 14, 14, 28, 42, 1, 15, ...
a(2) = 0 since a(1) = 1 sets a record in a, hence 0 terms in a exceed it. We set s = {1}.
a(3) = 1 since a(2) = 0 and is new to a, and 1 term (1) exceeds it. We set s = {0, 1}.
a(4) = 1 since a(1) = a(3) = 1, and the least used term u = 0, thus a(n) + u = 1 + 0 = 1.
We drop the first term of s and end up with s = {1, 1}.
a(5) = 2 since 1 is already in a, and the least used term u = 1, thus a(n) + u = 1 + 1 = 2.
We drop the first term of s to end up with s = {1, 1}.
a(6) = 0 since a(5) = 2 sets a record in a, hence nothing in a exceeds it. We set s = {1, 1, 2}.
a(7) = 1 since a(6) = 0 appeared before; the least used term u = 1, thus a(n) + u = 0 + 1 = 1.
We drop the first term of s to end up with s = {0, 1, 2}.
a(8) = 1 since a(7) = 1 appeared before; the least used term u = 0, thus a(n) + u = 1 + 0 = 1.
We drop the first term of s to end up with s = {1, 1, 2}.
a(8) = 2 since a(8) = 1 appeared before; the least used term u = 1, thus a(n) + u = 1 + 1 = 2.
We drop the first term of s to end up with s = {1, 1, 2}.
a(9) = 3 since a(8) = 2 appeared before; the least used term u = 1, thus a(n) + u = 2 + 1 = 3.
We drop the first term of s to end up with s = {1, 2, 2}.
etc.
This sequence can be generated by Code 1.
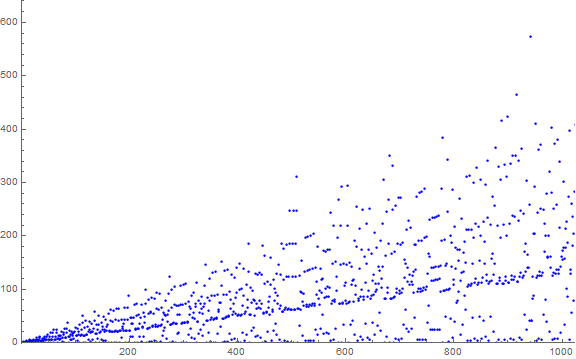
Figure 1.1 is a scatterplot of a(n) for 1 ≤ n ≤ 210. (Click here for an extended scatterplot of a(n) for 1 ≤ n ≤ 218).
Let Condition 0 pertain to novel a(n) and let Condition 1 pertain to extant a(n) = a(k) for 1 ≤ k < n.
Let sequence b record the conditions deployed by the algorithm behind a:
0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, ...
Therefore, a(1) and a(2) are novel and a(3) is extant i.e., a(3) appears at a(k) for 1 ≤ k < n, namely a(1) = a(3), etc. hence b(1) = b(2) = 0 and b(3) = 1. We can take indices j of 0s or 1s in b to identify the instigating condition that generates a(n+1).
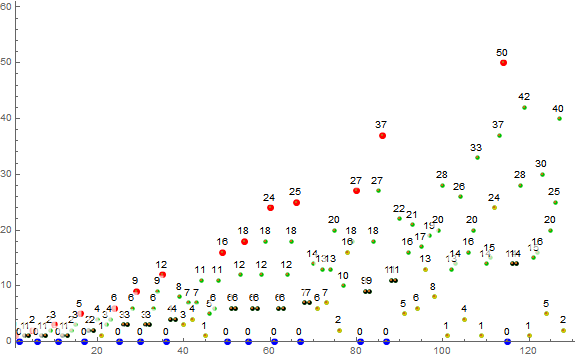
Figure 1.2 is a labeled scatterplot of a(n) for 1 ≤ n ≤ 27. Records a( j) = r appear in red, zeros in blue, repeated terms that follow 0 in black, terms instigated by novel m in gold and by extant m in green.
Outside of the series of nondecreasing terms that follow 0, the sequence a may prove turbulent. Therefore there are nondecreasing phases and turbulent phases in a. These phases may be classified.
Figure 1.3 is a labeled line plot of a(n) for 1 ≤ n ≤ 28.
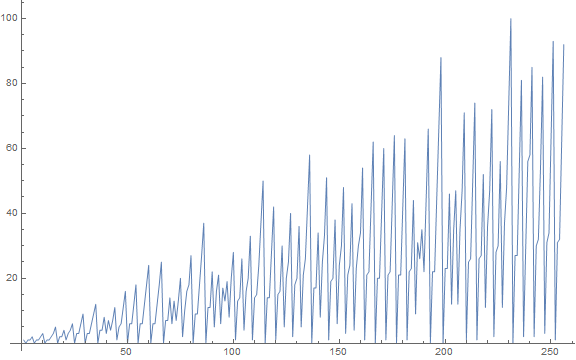
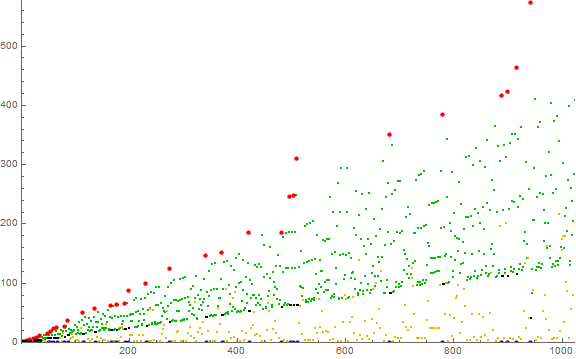
Figure 1.4 is a scatterplot of a(n) for 1 ≤ n ≤ 210. Records a( j) = r appear in red, zeros in blue, repeated terms that follow 0 in black, terms instigated by novel m in gold and by extant m in green. (Click here for an extended scatterplot of a(n) for 1 ≤ n ≤ 216 using this color function).
Sequence u that records the least used term.
We define a second sidecar sequence u(n) = s(1) for all n:
1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 2, 2, 2, 0, 2, 2, 2, 1, 2, 3, 3, 0, 3, 3, 3, 3, 0, 3, 3, 3, 4, 4, 0, 4, 4, 4, 3, 3, 4, 4, 4, 1, 5, 5, 6, 6, 0, 6, 6, 6, 6, 0, 6, 6, 6, 6, 6, 0, 6, 6, 7, 7, 7, 0, 7, 7, 7, 6, 6, 7, 8, 8, 2, 2, 9, 9, 9, 0, 9, 9, 10, 11, 11, 0, 11, 11, 11, 5, 11, 11, 6, 6, 12, 12, 8, 12, 12, 1, 12, 12, 12, 4, 13, 13, 13, 1, 13, 13, 13, 14, 14, 0, 14, 14, 14, 14, 1, ...
This sequence has offset 2, since we enter a(n) into its place in s after a(n+1).
We find those least used terms u( j − 1) that are addends to a(n) in Condition 1 in a sequence U:
0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 2, 2, 0, 2, 2, 1, 2, 3, 0, 3, 3, 3, 0, 3, 3, 3, 4, 0, 4, 4, 3, 4, 4, 1, 5, 5, 6, 0, 6, 6, 6, 0, 6, 6, 6, 6, 0, 6, 6, 7, 7, 0, 7, 7, 6, 7, 8, 2, 9, 9, 0, 9, 9, 10, 11, 0, 11, 11, 5, 11, 6, 12, 8, 12, 1, 12, 12, 4, 13, 13, 1, 13, 13, 14, 0, 14, 14, 14, 1, 14, 15, 5, 15, 16, 2, 16, 16, 5, 16, 16, 17, 0, 17, 17, 8, 18, 18, 1, 18, 18, 6, 18, 18, 3, 19, 19, 4, 20, 20, 1, ...
Figure 2.1 is a labeled scatterplot of u(n) for 1 ≤ n ≤ 27. Addends in U deployed via Condition 1 are colored red and labeled, while those not in U are in blue. We a line of terms persist for which we have multiple copies in s which seem to form an upper bound for u.
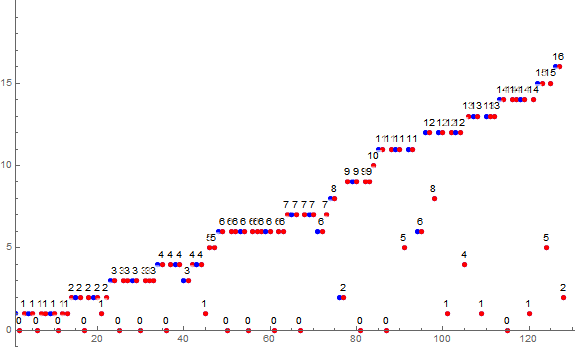
Figure 2.2 is a scatterplot of u(n) for 1 ≤ n ≤ 216.
Series instigated by records r.
Records r in a:
1, 2, 3, 5, 6, 9, 12, 16, 18, 24, 25, 27, 37, 50, 58, 62, 64, 66, 88, 100, 124, 146, 151, 185, 186, 247, 248, 311, 351, 384, 416, 423, 464, 574, 610, 638, 656, 675, 793, 806, 838, 928, 1023, 1097, 1186, 1198, 1208, 1353, 1417, 1422, 1424, 1781, 1899, 1924, 2021, 2096, 2109, 2114, 2164, 2256, 2267, 2382, 3053, 3216, 3433, ...
Indices j of records:
1, 5, 10, 16, 24, 29, 35, 49, 54, 60, 66, 80, 86, 114, 136, 166, 176, 192, 198, 231, 274, 341, 371, 421, 481, 497, 503, 510, 681, 779, 888, 899, 915, 941, 1273, 1284, 1393, 1402, 1460, 1564, 1594, 1756, 1827, 2020, 2251, 2351, 2566, 2654, 2806, 2864, 2870, 2877, 3726, 4037, 4095, 4111, 4275, 4304, 4310, 4412, 4637, ...
For record a( j) = r, a( j + 1) = 0, a( j + 2) = a( j + 3) = u( j). Records r are by definition unprecedented and nothing in a(k) for k < n exceeds r, hence per Condition 0, r → 0. For n > 2, 0 is extant and instigates Condition 1. Therefore we have:
r → 0 → u( j) → u( j).
since Condition 1 adds 0 + u( j) = u( j) for the first of the two repeated terms, and u( j) + 0 = u( j) for the second, exhausting the recently prepended 0 in s. Zeros in a are prepended to s and are of course exhausted immediately in the next iteration of Condition 1. If m = u( j) is extant, we often see a series of multiples im following the duplicated terms m. These multiples are sustained so long as u = m. The series is nondecreasing so long as the terms m in the series are extant. Whereupon a new m results from Condition 1, a(n) tends to collapse, though some large novel-instigated m can result, e.g., a(78) = 16. Generally, the repeated u( j) represent a lower bound for terms instigated by Condition 1. This is evident in Figure 2.1.
Sequence z includes terms u( j) repeated after the zeros that follow records:
1, 1, 1, 2, 3, 3, 4, 6, 6, 6, 7, 9, 11, 14, 17, 20, 21, 22, 23, 27, 33, 42, 45, 52, 59, 62, 62, 63, 83, 97, 111, 112, 114, 41, 154, 155, 173, 174, 183, 196, 200, 221, 231, 255, 282, 296, 320, 330, 346, 356, 356, 357, 472, 507, 513, 516, 537, 541, 542, 551, 577, 578, 195, 717, 741, 865, 352, 970, 1085, 1113, 286, 1509, 1596, 1663, 1673, 1709, 1756, 1766, 1851, 1946, 1948, 1990, 2004, 2120, 2271, 2496, 795, 515, 439, 4567, 1346, 1698, 5304, 1865, 5559, 5740, 6090, 1989, 2533, 7246, 7264, 8083, 8615, 8742, 9096, 3547, 10616, 10805, 3080, 11321, 1957, 2331, 4262, 17264, 17879, 4974, 18364, 19710, 5445, 21734, 22203, 22470, 22555, 23483, 24298, 4887, 5814, 3071, 3801, ...
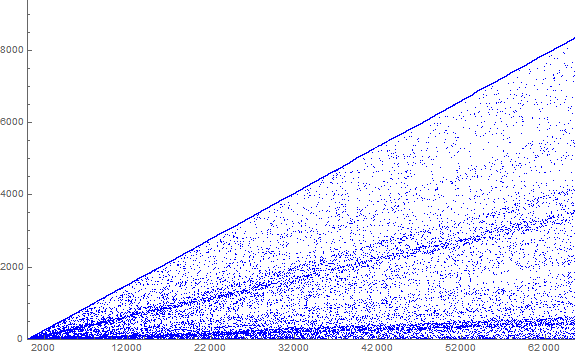
Figure 3.1 is a scatterplot of z:
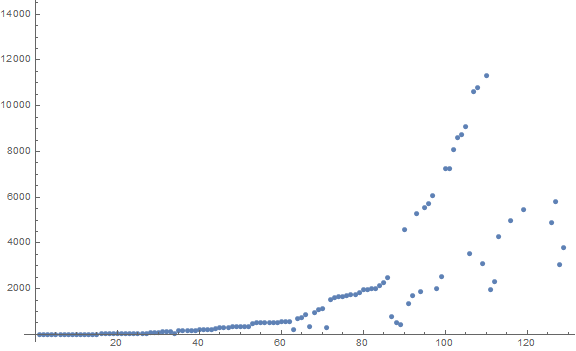
Figure 3.2 is a labeled scatterplot of u(n) for 1 ≤ n ≤ 27. The color function labels u( j) repeated after zeros in a in red, u( j) deployed through Condition 1 in blue, and latent least used u( j) in gray. (Click here for an expanded annotated plot of u(n) for 1 ≤ n ≤ 212 using this color scheme.
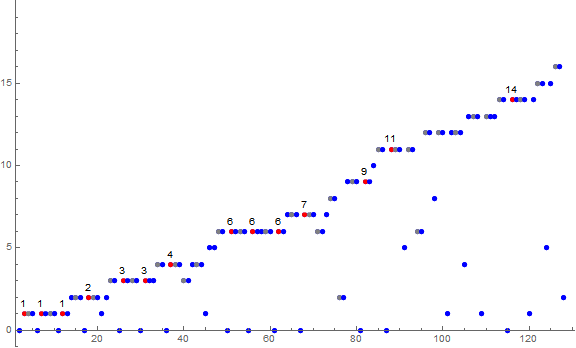
The general pattern has u( j) occur among terms in the prominent line at the top of Figure 3.1. The first catastrophe among the u( j) has a(942) = 0 followed by 2 copies of u(942) = 41 = z(34), which is not on the prominent line that is generally in the mid 100s for n = 942.
The sum of pairs of adjacent terms.
Let t(n) = a(n) + a(n + 1). Unlike the Van Eck sequence, the sum of pairs of adjacent terms in a exceeds n. The smallest case is t(509) = 559. The case involves the 3rd and 4th terms m, i.e., a(509) = 248 and a(510) = 311, in a series following a 0 instigated by the record a(503) = 248:
… → 248 → 0 → 62 → 62 → 124 → 186 → 248 → 311 → 0 → …
t(n) > n for n in the following sequence:
509, 2876, 5246, 5956, 7736, 8646, 8878, 15770, 15903, 16908, 18012, 19795, 20783, 22889, 23320, 27540, 27874, 32956, 33111, 36004, 41675, 42898, 43680, 45206, 48040, 49309, 54541, 56987, 57115, 63476, 67612, 68592, 71392, 82313, 83128, 84616, 88738, 92141, 99762, 109462, 111745, 119391, 122170, 123402, 135149, 140021, 143859, 143899, 143996, 154473, 159395, 169984, 175580, 176260, 183635, 190227, 203156, 212080, 213393, 222445, 233771, 238565, 243500, 255448, 261573, ...
Figure 4 is a labeled scatterplot of t(n) = a(n) + a(n + 1) for 1 ≤ n ≤ 29. The index is n. The dashed pink line indicates n = t(n).
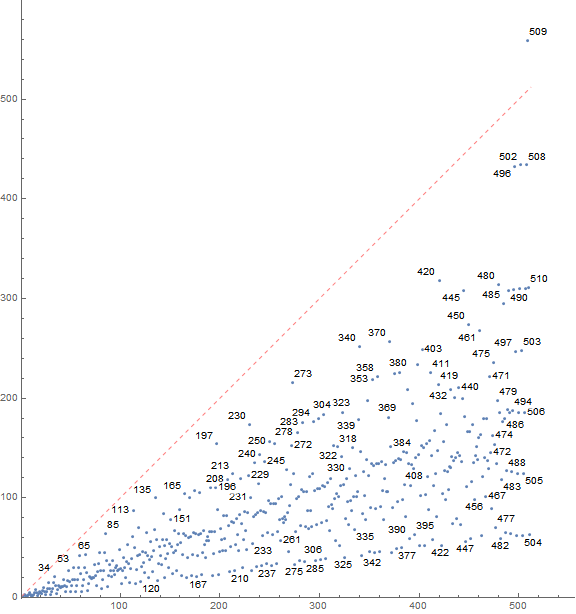
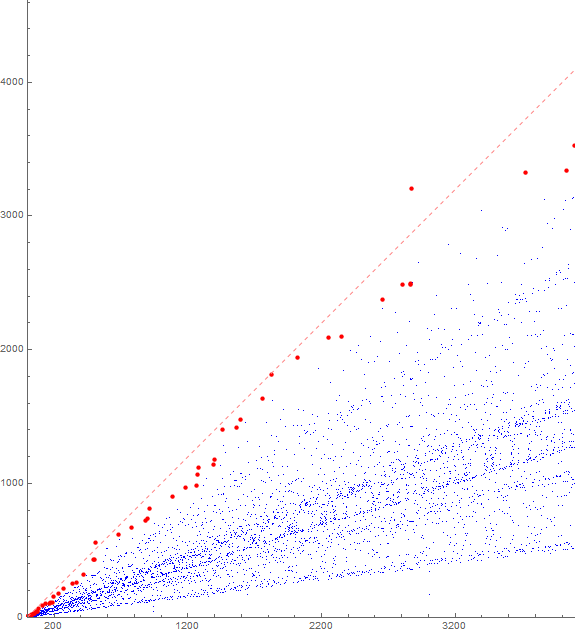
Figure 5 is a scatterplot of t(n) = a(n) + a(n + 1) for 1 ≤ n ≤ 212. The dashed pink line indicates n = t(n), and large red dots indicate records in t(n).
This concludes our examination.
Appendix:
Block[{a = {1}, s = {}},
Do[If[FreeQ[#2, #1],
AppendTo[a, Count[#2, _?(# > a[[-1]] &)] ],
AppendTo[a, a[[-1]] + First[s] ]; Set[s, Rest@ s]] & @@
{First[#1], #2} & @@ TakeDrop[a, -1];
Set[s, Insert[s, a[[-2]], LengthWhile[s, # < a[[-2]] &] + 1]], {i, 2^14}]; a]
Concerns OEIS sequences:
A181391: The Van Eck sequence.
A343887: a(n).
Document Revision Record.
2021 0503 1045 (Draft).