Numbers m such that (τ(m), P( j)) = 1.
A sequence by Michael Thomas De Vlieger, St. Louis, Missouri, 2022 0316.
Abstract.
We examine the number of divisors of n and its value mod P( j), whereP( j) is the product of the first j primes.
Introduction.
Given standard form prime power decomposition of n:
n = ∏_{p|n} pε.
we may define the divisor counting function as the cardinality of terms in the tensor product of prime power ranges p⁰, …, pε:
τ(n) = pε_{p|n} (ε + 1)
From this formula it is clear and generally well-known that τ(n) = k is odd iff n = m², that is, n ∈ A290. One way to look at this is k ≡ 1 (mod 2) iff all (ε + 1) ≡ 1 (mod 2), hence, ε ≡ 0 (mod 2). Any zeros (mod 2) produce k ≡ 0 (mod 2), i.e., even k. Of course, k ≡ 1 (mod 2) is the same as k : (k, 2) = 1, which we may express as k : k ⊥ 2.
We observe that obviously, odd k belong to { ±1 ∧ 3 } (mod 6). Consider that we may write k ≡±1 mod 6 as k : (k, 6) = 1, i.e., k : k ⊥ 2 ∧ k ⊥ 3. To produce a tensor product k coprime to 6, we need m² : m is a powerful number (m ∈ A1694). This is because, though we can produce n : n = m² ∧ τ(m²) ⊥ 6 through numbers {m⁰, m⁴, m⁶, m¹⁰, …}, we also need numbers like 72² = 5184 = 2⁶ × 3⁴, 108² = 2⁴ × 3⁶, etc. Thus, numbers that are powers (i.e., A1597) is not a sufficient condition for m.
Let S = A1694 = { a² × b³ : a ≥ 1, b ≥ 1 }. We observe A1694 ⊃ A290, that is, S contains all squares m² as well as other numbers like 72 = 2³ × 3² and 8 = 2³ that are nonsquare. Then sequence T = A076400 = { τ(A1694) }, which begins as follows:
1, 3, 4, 3, 5, 3, 4, 6, 9, 3, 7, 12, 5, 9, 12, 3, 4, 8, 15, 3, 9, 12, 16, 9, 6, 9, 18, 3, 15, 4, 3, 12, 15, 20, 9, 9, 12, 10, 3, 21, 5, 20, 12, 9, 7, 15, 18, 3, 24, 27, 3, 12, 18, 16, 11, 9, 12, 24, 9, 9, 25, 12, 4, 12, 3, 12, 9, 9, 18, 21, 3, 28, 27, 36, 3, 15, 24, 20, 15, 12, 9, 8, 4, 3, 27, 12, 5, 15, 30, 9, 36, 15, 16, 3, 12, 21, 9, 12, 6, 21, 24, 9, 12, 9, 16, 32, 3, 36, 45, 3, 9, 18, 30, 15, 24, 13, 9, 12, 27, 3, ...
In examining { A076400² mod 6 }, we find that the residue 3 seldomly appears:
1, 5, 1, 5, 3, 5, 1, 5, 1, 5, 1, 5, 3, 1, 5, 5, 1, 3, 3, 5, 1, 5, 1, 1, 5, 5, 1, 5, 3, 1, 5, 5, 3, 3, 1, 1, 5, 1, 5, 5, 3, 3, 5, 1, 1, 3, 1, 5, 5, 5, 5, 5, 1, 1, 3, 1, 5, 3, 1, 1, 3, 5, 1, 5, 5, 5, 1, 1, 1, 5, 5, 1, 5, 1, 5, 3, 5, 3, 3, 5, 1, 3, 1, 5, 1, 5, 3, 3, 3, 1, 1, 3, 1, 5, 5, 5, 1, 5, 5, 5, 3, 1, 5, 1, 1, 3, 5, 1, 3, 5, 1, 1, 3, 3, 5, 1, 1, 5, 5, 5, ...
Hence we find k ≡±1 mod 6 = { m = a² b³ : τ((a² b³)²) ⊥ 3 ∧ a ≥ 1, b ≥ 1 } = A350014. Thus, A350014 ⊂ A1694. The first terms of A350014 are as follows:
1, 4, 8, 9, 25, 27, 32, 36, 49, 64, 72, 100, 108, 121, 125, 169, 196, 200, 216, 225, 243, 256, 288, 289, 343, 361, 392, 441, 484, 500, 512, ...
We observe that this list includes composite prime powers (“multus” numbers, m ∈ A246547) and products of composite prime powers (“plenus” numbers, m ∈ A286708), and that A1694 = ∪({1}, A246547, A286708). That A350014 ought to include both nontrivial species of powerful number is easily shown by examination of exponents of prime power factors of m in the light of the divisor counting function formula.
Eldar adds the following limit in the comments of A350014:
∑_{n ≥ 1} 1/A350014(n) = 15 × ζ(3) / π²
We write a sequence { M : τ(M) ⊥ 6 } = { A350014² } = A352475. It is clear that M ∈ A1694 as well. The first terms of A352475 are as follows:
1, 16, 64, 81, 625, 729, 1024, 1296, 2401, 4096, 5184, 10000, 11664, 14641, 15625, 28561, 38416, 40000, 46656, 50625, 59049, 65536, 82944, 83521, 117649, 130321, ...
Eldar shows A352475 = A290 ∩ A336590, since the prime power decomposition of M restricts exponents ε ≡r : r ∈ {0, 4} mod 6 (cf. A047233). He also comments on limits:
∑_{n ≥ 1} 1/A352475(n) = π2/9.
Eldar adds the following attribited to Hilberdink [1]:
| m ≤ x | = (ζ(3/2)/ζ(2)) × x1/4 + (ζ(2/3)/ζ(4/3)) × x1/6 + O(x(1/8 + ε)), ∀ ε > 0
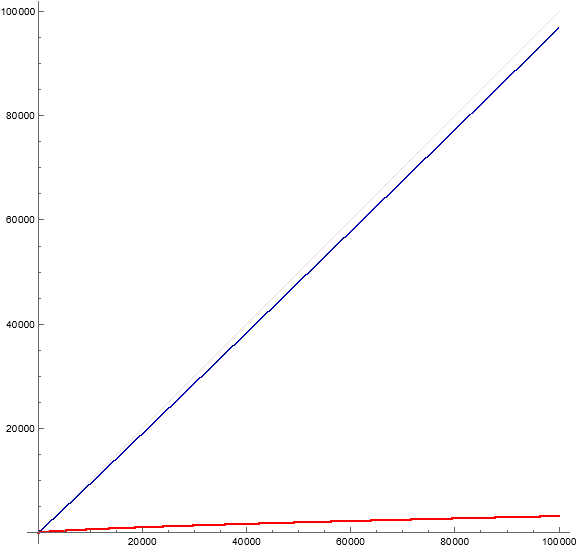
We may define the complementary sequence A355058 = { m = a² b³ : 3 | τ((a² b³)) ∧ a ≥ 1, b ≥ 1 } = { A290 \ A352475 } (with respect to the sequence of squares). This sequence has a much greater density than that of A352475. Even the sequence A354799 = { A1694 \ A350014 } = { m = a² b³ : τ((a² b³)) ⊥ 3 ∧ a ≥ 1, b ≥ 1 } has much greater density than A350014:
Figure 1: Plot | m | : τ(m²) ⊥ 3 in red and | m | : 3 | τ(m²) in dark blue, where the light gray line represents | m | for m = 1…10⁵.
Generalization.
Let’s generalize k : k ⊥ 2 to k : k ⊥ P( j), where P( j) = A2110( j) is the product of the first j primes. We can rewrite k : k ⊥ 2 as k ⊥ P(1) = A290. Then k ⊥ P(2) = A350014.
We return to the consideration of k : k ⊥ 2 = A290. Generalizing, we may write k : k ⊥ p for p prime. We saw in the case of p = 2, k ≡ 1 (mod 2) iff all (ε + 1) ≡ 1 (mod 2), since any residues that are 0 (mod 2) would result in k ≡ 0 (mod 2) via multiplication. We can also say that k ⊥ p iff all (ε + 1) ⊥ p, since any (ε + 1) : p | (ε + 1) forces a product also divisible by p.
Suppose p = 3. We can also say that k ⊥ 3 iff all (ε + 1) ⊥ 3, since any (ε + 1) : 3 | (ε + 1) forces a product also divisible by 3. Therefore, for most n = m², 3 | τ(m²), and since we know τ(m²) is odd, we may further say m : τ(m²) ≡ 3 (mod 6) is more commonly seen than m : τ(m²) ≡ ±1 (mod 6).
Generally, we may say that, for prime p, p | τ(n) more often than p ⊥ τ(n), and increasingly this is so as p increases.
We should thus expect the following to also be rare:
m : τ(m²) ≡ t (mod 30) : t ∈ {±1, ±7, ±11, ±13}.
We may instead more succinctly generalize this increasingly rare form as follows:
m : τ(m) ⊥ P( j) ∧ j ≥ 1.
As j increases, numbers of this form are increasingly rare.
Eldar posed A354178 = { n : τ(n) ⊥ P(3) } = { n : τ(n) ⊥ 30 } and A354179 the square roots of A354178. The former begins as follows:
1, 64, 729, 1024, 4096, 15625, 46656, 59049, 65536, 117649, 262144, 531441, 746496, 1000000, 1771561, 2985984, 3779136, 4194304, 4826809, 7529536, 9765625, 11390625, 16000000, ...
OEIS A358001 = { n : τ(n) ⊥ P(4) } = { n : τ(n) ⊥ 210 } and A358250 the square roots of A358001. The former begins as follows:
1, 1024, 4096, 59049, 65536, 262144, 531441, 4194304, 9765625, 43046721, 60466176, 241864704, 244140625, 268435456, 282475249, 387420489, 544195584, 1073741824, 2176782336, 3869835264, ...
We may continue with { n : τ(n) ⊥ P(5) } = { n : τ(n) ⊥ 2310 }, whose first terms are listed below:
1, 4096, 65536, 262144, 531441, 4194304, 43046721, 244140625, 268435456, 387420489, 1073741824, 2176782336, 13841287201, 31381059609, 34828517376, 68719476736, 139314069504, 152587890625, ...
Given a limit x = 2¹⁰⁰, we find the following cardinalities | { m : τ(m) ⊥ P( j) ∧ j = 2..12 } |:
53218215*, 183412, 4658, 1264, 406, 205, 107, 63, 44, 30, 23, ...
* calculated using Hilberdink’s formula.
Let U = A350014(1..2¹⁶). The cardinality of n : τ(n) ⊥ P(3) in U is 2061, and for P(4) it is 238, P(5), it is 100, etc. The table below shows cardinality c in U with a number of divisors coprime to P( j). Also listed in row j are the least number ℓ : τ(ℓ) ⊥ P( j), the least such m that is not a power of 2, and the least such n that is not a perfect power.
j c l m n
----------------------------------------------
2 65536 2^2 6^2 72 = 2^3 * 3^2
3 2061 2^3 6^3 864 = 2^5 * 3^3
4 238 2^5 6^5 15552 = 2^6 * 3^5
5 100 2^6 6^6 186624 = 2^8 * 3^6
6 47 2^8 6^8 3359232 = 2^9 * 3^8
7 27 2^9 6^9 40310784 = 2^11 * 3^9
8 17 2^11 6^11 2902376448 = 2^14 * 3^11
Conclusion.
This concludes our examination.
Appendix.
References:
[1] Titus Hilberdink, How often is d(n) a power of a given integer?, J. Num. Theory (2022) Vol. 236, 261-279.
Code 1:
With[{nn = 1500}, Select[Union@ Flatten@ Table[a^2*b^3, {b, nn^(1/3)}, {a, Sqrt[nn/b^3]}], Mod[DivisorSigma[0, #^2], 3] != 0 &]];
Concerns sequences:
A000005: The divisor counting function τ(n).
A000290: Perfect squares.
A001694: Squareful numbers, numbers that are not squarefree.
A076400: { τ(A1694) }.
A246547: “Multus” numbers, i.e., composite prime powers; A246547 ⊂ A1694.
A286708: “Plenus” numbers, i.e., products of multus numbers; A286708 ⊂ A1694.
A350014: Sequence h : a(n) = { m : τ(m²) ≡ ±1 (mod 6) } i.e., { m : τ(m²) ⊥ 6 }.
A352475: h²
= { m : τ(m) ≡ ±1 (mod 6) } i.e., { m : τ(m) ⊥ 6 }.
A354178: { m : τ(m) ⊥ 30 }.
A354179: { m : τ(m²) ⊥ 30 }.
A354799: { m : τ(m²) ≡ 3 (mod 6) } = { A1694 \ A350014 }.
A355058: { m : τ(m) ≡ 3 (mod 6) } = { A290 \ A352475 }.
A358001: { m : τ(m) ⊥ 210 }.
A358250:
{ m : τ(m²) ⊥ 210 }.
Document Revision Record.
2022 0316 2215 Draft.
2022 1207 1230 Draft 2.