OEIS A350150
A sequence by David Sycamore, this page written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 1215.
Abstract.
Analysis of A350150, explaining bifurcation into squares and nonsquares (an α and a β trajectory), evident in the scatterplot based on parity of the payload function, which is tantamount to index parity. We also explain the toggling of “flare” features instigated by 3 | τ(a(2n−1)) in regular α that end when the β trajectory of nonsquare terms cures. The sequence A350150 is one that is characterised both by intercalated squares and nonsquares governed by 2 | τ(a(n)), and by alternating phases governed by 3 | τ(a(n)). Theorems appear near the conclusion.
Introduction.
Let a(1) = 1 and let a(n+1) be the least k not already in a such that gcd(τ(a(n)), τ(k)) = 1. This is tantamount to the mappings of the following function f(x):
{f( j) : j = a(n−1) ∧ k ∈ ℕ ∧ u ∉ a : ∀ m < u : m ∈ a | k ∉ a(1..n−1) ∧ (τ(j), τ(k)) = 1 }
where a(1) = 1.
We have the following axioms:
Axiom 1. Coprimality: a(n+1) = k : τ(j) ⊥ τ(k).
Axiom 2. Inequality: k ∉ a(1..n−1), ∴ j ≠ k.
Axiom 3. Greedy: Let k : τ(j) ⊥ τ(k) and let k' : τ(j) ⊥ τ(k' ) ∧ k < k'. a(n+1) = k.
Axiom 4. a(n) is nonnegative.
The first terms of a follow:
1, 2, 4, 3, 9, 5, 16, 6, 25, 7, 36, 8, 49, 10, 64, 11, 81, 12, 625, 13, 100, 14, 121, 15, 144, 17, 169, 19, 196, 21, 225, 22, 256, 23, 289, 24, 324, 26, 361, 27, 400, 29, 441, 30, 484, 31, 529, 33, 576, 34, 676, 35, 729, 18, 1024, 20, 1296, 28, 2401, 32, 4096, 37, 784, 38, 841, 39, 900, 40, 961, 41, 1089, 42, 1156, 43, 1225, 46, 1369, 47, 1444, 48, 1521, 51, 1600, 53, 1681, 54, 1764, 55, 1849, 56, 1936, 57, 2025, 58, 2116, 59, 2209, 61, 2304, 62, 2500, 65, 2601, 66, 2704, 67, 2809, 69, 2916, 70, 3025, 71, 3136, 73, 3249, 74, 3364, 77, 3481, 78, ...
Code 1 generates the sequence efficiently, however there is code at OEIS A350150 that will generate a few hundred terms. Through an extensible version of Code 1, we have obtained a dataset of 3600000 terms.
Figure 1: Log-log scatterplot of a(n) for 1 ≤ n ≤ 210.
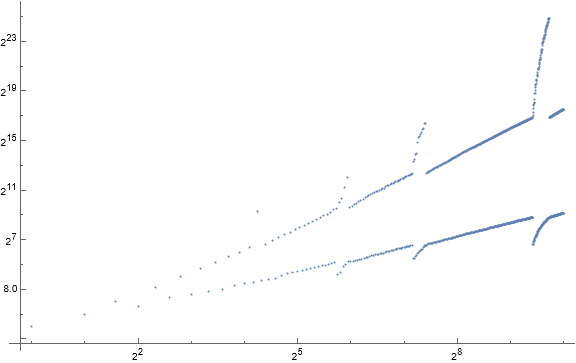
The most notable features of the scatterplot Figure 1 are bifurcation of even- and odd-indexed terms, and “flare” phases that happen approximately in a sort of exponential fashion.
Auxiliary sequences.
Define sequence d(n) = τ(a(n)); this sequence begins:
1, 2, 3, 2, 3, 2, 5, 4, 3, 2, 9, 4, 3, 4, 7, 2, 5, 6, 5, 2, 9, 4, 3, 4, 15, 2, 3, 2, 9, 4, 9, 4, 9, 2, 3, 8, 15, 4, 3, 4, 15, 2, 9, 8, 9, 2, 3, 4, 21, 4, 9, 4, 7, 6, 11, 6, 25, 6, 5, 6, 13, 2, 15, 4, 3, 4, 27, 8, 3, 2, 9, 8, 9, 2, 9, 4, 3, 2, 9, 10, 9, 4, 21, 2, 3, 8, 27, 4, 3, 8, 15, 4, 15, 4, 9, 2, 3, 2, 27, 4, 15, 4, 9, 8, 15, 2, 3, 4, 21, 8, 9, 2, 21, 2, 9, 4, 9, 4, 3, 8, 45, 2, 3, 10, 9, 4, 15, 2, 9, 4, 27, 4, 3, 4, 15, 8, 9, 2, 27, 4, 3, 4, 35, 6, ...
Records r begin as follows:
1, 2, 4, 9, 16, 25, 36, 49, 64, 81, 625, 676, 729, 1024, 1296, 2401, 4096, 4225, 4356, 4489, 4624, 4761, 4900, 5041, 5184, 10000, 11664, 14641, 15625, 28561, 38416, 40000, 46656, 50625, 59049, 65536, 82944, 83521, 84100, 84681, 85264, 85849, 86436, 87025, 87616, 88209, 88804, 89401, 90000, 90601, 91204, 91809, 92416, 93025, 93636, 94249, 94864, ...
Records in a are square with exception of r(2) = 2.
Minima s appear as follows:
1, 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 20, 28, 32, 37, 38, 39, 40, 41, 42, 43, 44, 45, 50, 52, 60, 63, 68, 72, 75, 76, 84, 90, 92, 94, 95, 96, 98, 99, 108, 116, 117, 124, 126, 132, 140, 147, 148, 150, 153, 156, 160, 164, 171, 172, 175, 180, 188, 198, 200, 204, 207, 212, 220, 224, 228, 234, 236, 242, 243, 244, 245, 252, 260, 261, 268, 275, 276, 279, 284, 288, 292, 294, 300, 306, 308, 315, 316, ...
These are nonsquares outside of s(0) = 1. The minima are tantamount to distinct terms in least unused u, which begins as follows:
1, 2, 3, 3, 5, 5, 6, 6, 7, 7, 8, 8, 10, 10, 11, 11, 12, 12, 13, 13, 14, 14, 15, 15, 17, 17, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 20, 20, 28, 28, 32, 32, 37, 37, 38, 38, 39, 39, 40, 40, 41, 41, 42, 42, 43, 43, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, 44, ...
The longest-held u include {44, 96, 450, 7848}, which are held for 70, 514, 10808, and 3527604 terms, respectively. Additionally, u = 18 is held for 28 terms, and there are many terms in the thousands held dozens of times, the number 720 held 20 times, etc. We term this the “persistence” of u. Given the dataset, term u = 7848 is the most persistent smallest missing number. We likewise call {(12), 18, 44, 96, 450, 7848, …} persistent unused terms. Figure 2 illustrates that these persistent unused terms serve as the floor for the collapse of β.
Code 2 provides Mathematica script that generate these auxiliary sequences.
Figure 2: Log-log scatterplot of a(n) for 1 ≤ n ≤ 212 showing maxima r in red and minima t in blue. The golden line indicates the least unused number u. For α, we label the odd-indexed term a(n−2) that precedes a flare phase a(n..n+m), and the final term a(n+m). For β we label the first and last terms in the flare phase. Generate this figure via Code 4. (Click for slightly enlarged version)
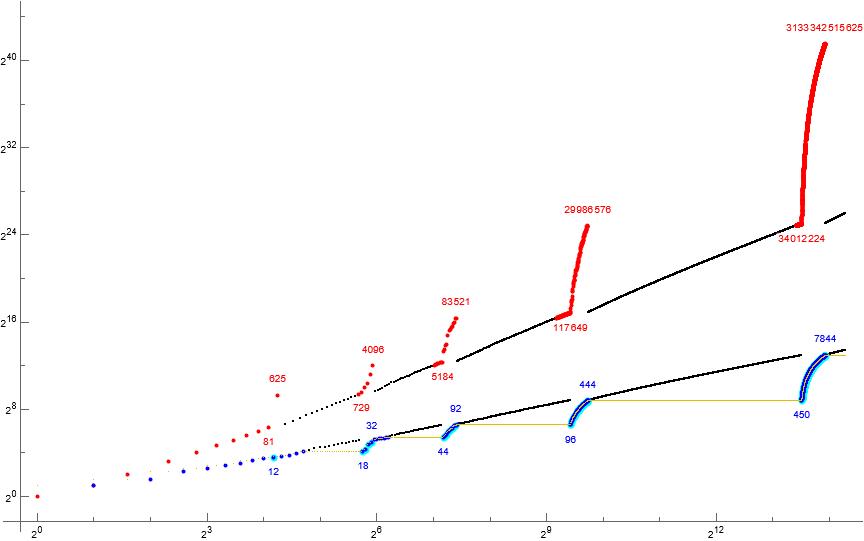
Bifurcation of the sequence.
Clearly the sequence is bifurcated according to even- and odd-indexed terms, that is, an α-trajectory a(2n+1) = k : τ(k) = 1 (mod 2) and a β-trajectory a(2n) = k : τ(k) = 0 (mod 2). Through examination we see that the terms k ∈ α are perfect squares (i.e., in A290) while the terms k ∈ β are nonsquares (i.e., in A37). (See Theorem 2.)
Hence, parity of τ(k) is the source of bifurcation into an α-trajectory of squares and a β-trajectory of nonsquares. This parity alternates odd and even-indexed a(n) as n increases, hence, parity of index n and that of τ(k) are interchangeable.
Alpha (α) trajectory: squares.
It is clear, given a(1), that f(a(1)) → k : 2 | τ(k). Any prime k may satisfy that criterion, but also any squarefree semiprime, etc. and the only k that do not satisfy are squares. Since a(2) is therefore nonsquare with an even number of divisors, a(3) must present f(a(2)) → k : τ(k) mod 2 ≡ 1. We see via induction that this leads to an infinite, alternating series of nonsquares and squares for even- and odd-indexed terms, since, for τ(k) > 1, there are an infinite number of k. Therefore, the sequence a is infinite.
Terms of α begin as follows:
1, 4, 9, 16, 25, 36, 49, 64, 81, 625, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 676, 729, 1024, 1296, 2401, 4096, 784, 841, 900, 961, 1089, 1156, 1225, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2500, 2601, 2704, 2809, 2916, 3025, 3136, 3249, 3364, 3481, ...
We may take the square root of α(i) to derive the following sequence S:
1, 2, 3, 4, 5, 6, 7, 8, 9, 25, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 32, 36, 49, 64, 28, 29, 30, 31, 33, 34, 35, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 65, 66, 67, 68, 69, 70, 71, 72, 100, 108, 121, 125, 169, 196, 200, 216, 225, 243, 256, 288, 289, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 101, 102, 103, 104, 105, 106, 107, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 122, 123, 124, 126, 127, 129, 128, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, ...
Beta (β) trajectory: nonsquares.
In S, it seems evident where flares occur in a; certain squares S(i)² occur ahead of schedule, while the remaining progression as i increases seems to also increase, of course, skipping S(i) that have already appeared. At a certain point, the sequence jumps back to where it had been interrupted to resume increase. (See Theorem 3.5.)
Terms of β begin as follows:
2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 19, 21, 22, 23, 24, 26, 27, 29, 30, 31, 33, 34, 35, 18, 20, 28, 32, 37, 38, 39, 40, 41, 42, 43, 46, 47, 48, 51, 53, 54, 55, 56, 57, 58, 59, 61, 62, 65, 66, 67, 69, 70, 71, 73, 74, 77, 78, 79, 80, 82, 83, 85, 86, 87, 88, 89, 91, 93, 44, 45, 50, 52, 60, 63, 68, 72, 75, 76, 84, 90, 92, 94, 95, 97, 101, 102, 103, 104, 105, 106, 107, 109, 110, 111, 112, 113, 114, 115, 118, 119, 120, 122, 123, 125, 127, 128, 129, 130, 131, 133, 134, 135, 136, 137, 138, 139, 141, ...
We find β(i) at A37( j) to generate sequence T of indices j:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15, 17, 18, 19, 20, 21, 22, 24, 25, 26, 28, 29, 30, 14, 16, 23, 27, 31, 32, 33, 34, 35, 36, 37, 40, 41, 42, 44, 46, 47, 48, 49, 50, 51, 52, 54, 55, 57, 58, 59, 61, 62, 63, 65, 66, 69, 70, 71, 72, 73, 74, 76, 77, 78, 79, 80, 82, 84, 38, 39, 43, 45, 53, 56, 60, 64, 67, 68, 75, 81, 83, 85, 86, 88, 91, 92, 93, 94, 95, 96, 97, 99, 100, 101, 102, 103, 104, 105, 108, 109, 110, 111, 112, 114, 116, 117, 118, 119, 120, 122, 123, 124, 125, 126, 127, 128, 130, ...
For small i, it seems that T behaves rather like S, but with missing terms in A37 accumulating to a certain point, then S drops to fill in all the gaps and then proceed more or less with S(i) in order of magnitude. Close inspection shows that there is some dithering, with A37( j+1) entering β before A37( j), but the latter entering immediately or soon after. Some gaps yet remain and only appear in the “clean up session” of the flare phase. This becomes evident when we take first differences D of T:
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 2, 1, 1, 2, 1, 1, -16, 2, 7, 4, 4, 1, 1, 1, 1, 1, 1, 3, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 1, 2, 1, 1, 2, 1, 3, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 2, -46, 1, 4, 2, 8, 3, 4, 4, 3, 1, 7, 6, 2, 2, 1, 2, 3, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 3, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 3, 2, 1, 2, 1, 2, 1, 1, 2, 2, 2, -3, 4, 1, ...
First differences D of sequence T reveals incrementation of j : A37( j) = β(i) = a(2i) or the most part, with j = j' + m : m > 1 ∧ j = T(i) ∧ j' = T(i−1) indicating skips. When β drops to a persistent least unused u, we have a “large” negative m = m'. followed by a phase of m often exceeding 1 until D “cures” when the sum of m immediately following m'.
The data in D also show instances of entry of A37( j) out of order, corrected immediately or soon afterward, for example, D(135) = −3, D(136) = 4. This corresponds to a(270) = 165, a(272) = 162. These instances pertain to the preference of τ(k) = 2ε : ε ≥ 0 over τ(k) with shallower totients.
Generate T and D via Code 3.
Governance of the sequence by α or β.
Consider the sequence d(n) = τ(a(n)) bifurcated into even- and odd-indexed terms, thus:
dα(i) = d(2n+1):
1, 3, 3, 5, 3, 9, 3, 7, 5, 5, 9, 3, 15, 3, 9, 9, 9, 3, 15, 3, 15, 9, 9, 3, 21, 9, 7, 11, 25, 5, 13, 15, 3, 27, 3, 9, 9, 9, 3, 9, 9, 21, 3, 27, 3, 15, 15, 9, 3, 27, 15, 9, 15, 3, 21, 9, 21, 9, 9, 3, 45, 3, 9, 15, 9, 27, 3, 15, 9, 27, 3, 35, 25, 35, 5, 7, 5, 25, 35, 49, 25, 11, 17, 55, 5, 3, 9, 15, 15, 9, 27, 3, 27, 9, 9, 3, 45, 9, 9, 9, 21, 3, 45, 9, 15, ...
dβ(i) = d(2n):
2, 2, 2, 4, 2, 4, 4, 2, 6, 2, 4, 4, 2, 2, 4, 4, 2, 8, 4, 4, 2, 8, 2, 4, 4, 4, 6, 6, 6, 6, 2, 4, 4, 8, 2, 8, 2, 4, 2, 10, 4, 2, 8, 4, 8, 4, 4, 2, 2, 4, 4, 8, 2, 4, 8, 2, 2, 4, 4, 8, 2, 10, 4, 2, 4, 4, 4, 8, 2, 4, 4, 6, 6, 6, 6, 12, 6, 6, 12, 6, 6, 12, 12, 6, 4, 4, 2, 2, 8, 2, 8, 8, 4, 2, 2, 8, 4, 10, 2, 8, 4, 4, 4, 16, 4, ...
Let M(n) = [ 3 | τ(a(n)) ], Iverson brackets. This sequence begins:
0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, ...
This sequence can also be broken into even- and odd-indexed subsequences:
Mα(i) = M(2n+1):
0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, ...
Mβ(i) = M(2n):
0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...
Toggling between α-control and β-control (or flare) phases.
Bifurcation of M lends the notion that there is complementarity between Mα and Mβ such that [ 3 | τ(a(n)) ] governs recurrent phases in the sequence. (See Theorem 3.1)
The first 17 terms of the sequence feature odd-indexed squares (i.e., m² in α) that may or may not present divisibility by 3 with no effect on the even-indexed nonsquare terms (i.e., k in β). (See Theorem 3.2)
Table 2.1 places the first odd indexed (α) terms, stated as m² above and intercalated with even indexed (β) terms, stated as k ∈ A37 (denoted by ⊠) below.
τ(m²)
1 3 3 5 3 9 3 7 5 5 9
a(2n+1) 1² (2²) (3²) 4² (5²) (6²) (7²) 8² 9² 25² (10²) ...
a(2n) 1⊠ 2⊠ 3⊠ 4⊠ 5⊠ 6⊠ 7⊠ 8⊠ (9⊠) 10⊠ ...
2 2 2 4 2 4 4 2 6 2
τ(k)
Though there was an opening for 3 | τ(k) in β in the wake of a(7) = 4², u = A37(4), and so a(8) = A37(4) = 6. It is fortunate that A37(9) = 12 = a(18) could enter the sequence “as expected”, that is, in order of A37, as τ(a(17)) = τ(9²) = 5. These are special cases.
Whereupon we have the first term a(2n) = k such that 3 | τ(k), and of course, 2 | τ(k) as well is it is in β, hence 6 | τ(k), the sequence is governed by [ 3 | τ(a(n)) ] as well as [ 2 | τ(a(n)) ]. (See theorem summary.)
Until a(18) = 12, we have only seen k : τ(k) mod 3 ≡ ±1 in β. Thereafter, given 3 | τ(m²) in α, we are forced into k : τ(k) mod 3 ≡ ±1. Consequently, nonsquares 18, 20, 28, and 32 are delayed in entering β until after the appearance of τ(m²) mod 3 ≡ ±1 in α at a(53) = 729 = 36. Thereafter we finally have a(54) = 18. (See Observation 3.3.)
A β number k : 3 | τ(k) forces m² into m : τ(m²) mod 6 ≡ ±1, that is, into the totient of 6, meaning the 5-rough numbers A7310. Hence, α consists of m² with some root m in A1694 : τ(m²) mod 3 ≡ ±1. Since we have nontrine τ(m²), we are allowed trine τ(k) until all laggard nonsquares have entered and β has k > a(52) = A37(30). (See Theorem 5.1.)
Let a(2n) = A37(i) and a(2n+1) = m² : τ(m²) mod 3 ≡ ±1. Generally, we say that β has “cured” whereupon k > A37(i) ∧ τ(k) mod 3 ≡ ±1. Thereafter, the following square is (m+j)² : j ≥ 1 ∧ 3 | τ((m+j)²). We see that the least (m+j)² : τ((m+j)²) mod 3 ≡ ±1 already were entered during the range when β demanded such, and that we won’t see such until we trigger another spate of admissions of denied k such that 3 | τ(k). Hence, we may surmise that the sequence will not experience another instance of a(2n+1) = m² : τ(m²) mod 3 ≡ ±1 until the largest square brought about by the last instance of trine τ(k) has been exceeded. (See Theorem 3.5.)
A necessary and sufficient font of alpha flare terms m².
In the β-control or “flare” phase, m in α (as m²) avoids A1694(i) : i ∈ {5, 13, 18, 19, 29, 33, 34, 41, 42, 46, 55, …}, and occurs in the sequence h = OEIS A350014 below:
1, 4, 8, 9, 25, 27, 32, 36, 49, 64, 72, 100, 108, 121, 125, 169, 196, 200, 216, 225, 243, 256, 288, 289, 343, 361, 392, 441, 484, 500, 512, 529, 576, 675, 676, 729, 800, 841, 864, 900, 961, 968, 972, 1000, 1089, 1125, 1156, 1225, 1323, 1331, ...
We maintain a file of 10000 terms of h for convenience.
Clearly h ⊂ A1694, however, a(147) = 108², m =108 ∈ A052486, not in A1597. Further, A290 ⊂ h, since m ∈ A290, i.e., m = j² has τ(m²) mod 3 ≡1, i.e., τ( j4) mod 3 ≡1. Prime power pε : ε mod 3 ≡0 ∨ 1 appears in h. We may thus derive A1694 \ h, that is , m in A1694 : 3 | τ(m²) = g. The terms in g begin:
16, 81, 128, 144, 324, 400, 432, 625, 648, 784, 1024, 1152, 1296, 1936, 2000, 2025, 2187, 2401, 2500, 2592, 2704, 3200, 3456, 3600, 3888, 3969, 4624, 5000, 5184, 5488, 5625, 5776, 6272, 7056, 8100, 8192, 8464, 8748, 9216, 9604, 9801, 10000, ...
The sequence g = A1694(5, 13, 18, 19, 29, 33, 34, 41, 42, 46, 55, …) and contains pε : ε ≡2 (mod 3) ∧ε > 1. Observations regarding the proportion of terms m ∈ g for A1694(1..24 i):
i: |g| / |A1694(1..2^(4i))|
1: 0.625
2: 0.8046875
3: 0.914306640625
4: 0.96356201171875
5: 0.9848432540893555
6: 0.9938033819198608
It is clear that most m ∈ A1694 are also in h, that is, 3 ⊥ τ(m²), hence most m in A1694 qualify for α in the β-control or flare phase.
In α, during flare phase I, a(17) = 9² = h(4)² precipitates the phase, which contains a(19) = 625 = 25² = h(5)². In flare phase II we see a(53) = 27² = h(6)² start the phase, which contains {32², 26², 49², 64²} = h(7..10)². In flare phase III we see a(143) = 72² = h(11)² start the phase, which contains h(12..24)², and in IV we have h(26..107)².
In flare phase V, the terms in h do not come in order, but h(109..2034)² appear after a(11663) = 5832² = h(108)² initiates the phase. The VI flare phase will begin whereupon h(2035)² = 1771561² = A1694(2714)² enters the sequence.
Generally, when m² : m ∈ h appears in α-control phase, the sequence A350150 toggles into β-control, then m² : m ∈ h appear generally sequentially unless preceding τ(k) in β is q-rough for prime q > 3. Therefore we may use h ⊂ A1694 as the font of a(2n+1) in the β-control or flare phase.
See Theorem 5.1 for more about h.
An expedited version of Code 1 based on toggling control and the principles outlined above appears at Code 6. Also included are means of generating A1694 and h.
Phases.
We turn our attention to these alternating phases. Such are exhibited in scatterplot characterized by the apparent behavior of the recursive mappings of fn( j) → k. We have observed bifurcation of a into trajectory α consisting of square k, and trajectory β consisting of nonsquare k based on parity of index n, which is tantamount to same parity of τ(k). (See Theorem 2.) The scatterplot shows a more or less regular progression of intercalated squares and nonsquares, which we shall call the “regular phase” (see Theorem 3.4), interrupted by “flare phases” (see Theorem 3.5) where β falls to persistent unused number u to admit missing u until it cures, consequently, τ(m²): m² in α are forced into the totient of a relatively low-totient τ(m²). (See Theorem 5.1.)
Figure 3: Log-log scatterplot of s(n) for 1 ≤ n ≤ 27 annotating a(n) in black above and τ(a(n)) in red below the point. The plot shows bifurcation of the function with a(2n) : τ(a(2n)) even in trajectory β below, while powerful a(2n+1) : τ(s(2n+1)) odd in trajectory α above. Terms a(2n) : τ(a(2n)) = 6 appear in blue, while a(2n+1) : τ(a(2n)) = 6 appear in red. The faint green line below is d(n) = τ(a(n)). Code 5 generates this plot.
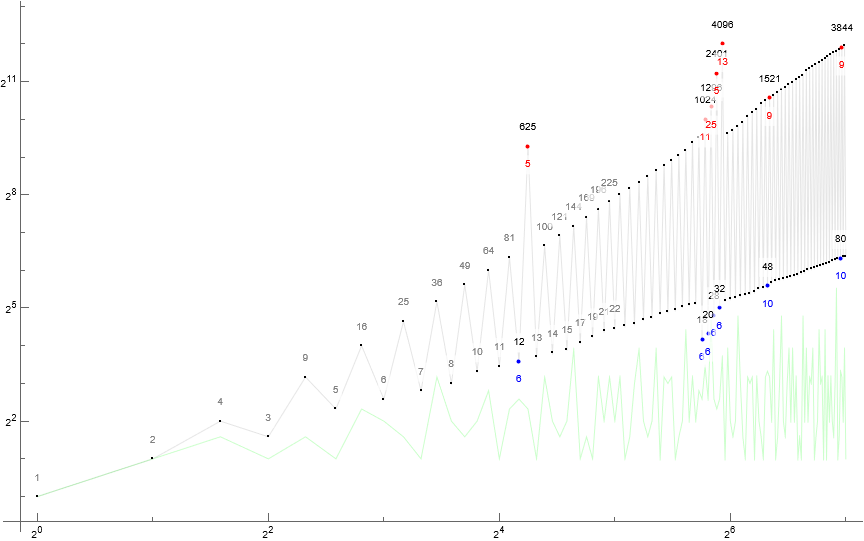
Let’s divide the sequence into intercalated regular and flare phases, designated by lowercase and uppercase Roman numerals, respectively for the sake of clear distinction.
Let a(2n−2) = A37(i) and a(2n−1) = A290( j).
We employ the fall in β, more precisely, the adoption of a(2n) = u, where u is persistent, i.e., A37(i) > A37( i' ) ∧ i > i' to significance, as the beginning of a flare phase. The first flare phase is evident by a second characteristic of all flare phases that have a(2n+1) = A290( j' ) >> A290( j) ∧ j << j'.
We regard the “cure” or return of trajectory β such that a(2n+2ℓ) = A37(i+1) and a(2n+2ℓ+1) = A290( j+1). It may be that we have instead a(2n+2ℓ) = A37(i+2), etc., but the notion is that we have returned to the regular behavior of the remappings that generate more or less generally increasing terms in both α and β trajectories, where the former is predominated by A290(i) < A290(i') ∧ i < i', and the latter is predominated by A37( j) < A37( j') ∧ j < j'. (See supplementary definitions, Corollaries 2.1 and 2.2)
From this, we derive these formulas for phase lengths:
ℓα= 2 × | {m ∈ h(α0..α1) : τ(k) mod 3 ≢ 0} | ,
where α0 is such that a(n) = h(α0) = v and a(n−1) = h(i), i > α0.
where α1 is such that a(n+ℓ) = h(α1) ∧ i < α1,
ℓα= 2 × (h(α1)² − | h(α0..α1) | )
= 2
× (h(α1)² − (α1 − α0)),
where α0 is such that a(n) = h(α0) = v and a(n−1) = h(i), i > α0.
where α1 is such that a(n+ℓ) = h(α1) ∧ i < α1.
Since we know that α1 − i = β1 − i = 1 (α and β “cure”), we can estimate the appearance of phases in A350150 using the formulas. These are estimates, because it is possible to have by chance, for example, 3 | τ(k) at the inception or emergence from β-control, etc., and thus delay.
Sequence a is considered regular until a(17), on account of the explosion of a(19) = 625, much greater than a(17) = 9² = h(4)². Let us take τ(a(2n+1)) mod 3 for the odd-indexed or α-trajectory terms, squares, for 1 ≤ n ≤ 9: {1, 0, 0, 2, 0, 0, 0, 1, 2}, and we see that there are several occasions of τ(a(2n+1)) mod 3 ≠ 0. (See Theorem 3.2 and Observation 3.3)
Flare phase (I) begins with a(18) = 12 = A37(9), τ(12) = 6, with a(19) = 625 = 25² = h(5)² >> a(17) = 81 = 9² = h(4)². a(20) = 13 = A37(10) represents β-cure and the start of the next regular phase.
Regular phase (ii) begins thus at a(20) and ends at a(53). We note that the α trajectory in (ii) consists of k : 3 | τ(k), except a(53) = 27² = h(6)² with τ(a(53)) = 7, which precipitates a(54) = u = 18.
Flare phase (II) begins with a(54) = 18 = A37(14), τ(18) = 6, seeing a(52) = 35 = A37(30). The succeeding alpha-term a(55) = 1024 = 32² = h(7)² >> a(53) = 729 = 27². The squares in this phase include {32², 26², 49², 64²} = h(7..10)². a(62) = 37 = A37(31) represents β-cure and the start of the next regular phase.
Regular phase (iii) begins thus at a(62) and ends at a(143). The squares in this phase are missing those that appeared in flare phase (II). We note that the α trajectory in (iii) consists of k : 3 | τ(k), except a(143) = 72² = h(11)² with τ(a(143)) = 35, precipitating a(144) = u = 44.
Flare phase (III) begins with a(144) = 44 = A37(38), τ(44) = 6, seeing a(142) = 93 = A37(84). The succeeding alpha-term a(145) = 100² >> a(143) = 72². The m² in this phase include h(12..24)². The m in h(12..24) appear below:
100, 108, 121, 125, 169, 196, 200, 216, 225, 243, 256, 288, 289
a(170) = 94 = A37(85) represents β-cure and the start of the next regular phase.
Regular phase (iv) begins thus at a(170) and ends at a(685). We note that the α trajectory in (iv) consists of k : 3 | τ(k), except a(685) = 343² = h(25)² with τ(a(685)) = 7, which precipitates a(686) = u = 96.
Flare phase (IV) begins with a(686) = 96 = A37(87), τ(96) = 12, seeing a(684) = 445 = A37(424). The succeeding alpha-term a(687) = 361² = h(26)² >> a(685) = 343². The m² in this phase include h(26..107)². The roots m in h(26..107) appear below:
361, 392, 441, 484, 500, 512, 529, 576, 675, 676, 729, 800, 841, 864, 900, 961, 968, 972, 1000, 1089, 1125, 1156, 1225, 1323, 1331, 1352, 1369, 1372, 1444, 1521, 1568, 1600, 1681, 1728, 1764, 1800, 1849, 1944, 2048, 2116, 2197, 2209, 2304, 2312, 2601, 2700, 2744, 2809, 2888, 2916, 3025, 3087, 3125, 3136, 3249, 3267, 3364, 3375, 3481, 3528, 3721, 3844, 3872, 4000, 4096, 4225, 4232, 4356, 4489, 4500, 4563, 4608, 4761, 4900, 4913, 5041, 5292, 5324, 5329, 5400, 5408, 5476
a(850) = 446 = A37(425) represents β-cure and the start of the next regular phase.
Regular phase (v) begins thus at a(850) and ends at a(11663). Squares m² that appeared in flare phase (IV) do not appear in α. We note that the α trajectory in (iv) consists of k : 3 | τ(k), except a(11663) = 5832² = h(108)² with τ(a(11663)) = 91, which precipitates a(11664) = u = 450.
Flare phase (V) begins with a(11664) = 450 = A37(429), τ(450) = 18, seeing a(11662) = 7845 = A37(7757). The succeeding alpha-term a(11665) = 5929² = h(109)² >> a(11663) = 5832². The squares m² in h(109..2034)² appear in α. (Refer to this file for a list of the roots m.) The largest square in this phase is a(15515) = 1770125² = A1694(2713)² = h(2034)². a(15516) = 7846 = A37(7758) represents β-cure and the start of the next regular phase.
Regular phase (vi) begins thus at a(11516). The persistent least missing number u = A37(7760) = 7848. We note that the α trajectory in (v) consists of k : 3 | τ(k); regular phase (vi) will end upon an instance of a(2n−1) : 3 | τ(a(2n−1)), except a(3543121) = 1771561² = h(2035)² with τ(a(3543121)) = 13, which precipitates a(3543122) = u = 7848.
Flare phase (VI) begins with a(3543122) = 7848 = A37(7760), τ(7848) = 24, seeing a(3543120) = 2421514 = A37(2419958). The succeeding alpha-term a(3543123) = 1773593² = h(2036)² >> a(3543121) = 1771561² = h(2035)².
Estimated phases.
Estimations for the remainder of flare phase (VI).
We arrive at this estimate via the following:
ℓβ = 2 × | {k ∈ A37(7760..2419958) : 3 | τ(k)} | = 2 × 648398 = 1296796.
Therefore, a(n+ ℓβ) = A37(β1+1) = A37(2419959) = 2421515 for n + ℓβ ≈ 4839918. a(4839918) with 4 divisors should represent β-cure and the start of the next regular phase. We expect ℓβ /2 = 648398 terms m² ∈ h in α, specifically, h(2035..650433)², not necessarily always in order. The largest square should be a(4839917) = h(650433)² = A1694(886993) = 169687148761² = 28793728454637743835121 = 134 × 316874. Therefore we expect m² ∈ h(2035..650433)² to appear in flare phase (VI) and be missing in regular phase (vii) thereafter.
Regular phase (vii) therefore should begin at a(4839918), followed by a(4839919) = 1771562² with 81 divisors. The first nonsquare denied in regular phase (vii) should be A37(2419960) = 2421516 with 24 divisors; it therefore should be the next persistent least missing number u. All the squares h(2035..650433)² which had τ(m²) ≡ ±1 (mod 6), and appeared early in flare phase (VI), have been depleted, and all other squares m² in the range 1771562 ≤ m < 169687148761 have τ(m²) ≡ 3 (mod 6).
We should have 169687148761 − (650433 − 2035) = 28793728454637743186723 squares in α, thus a(57587456909275488145008) = 28793728454807430335484² = 829078798329187089767548777070131804789514256 = 24 × 34 × 653² × 773² × 1584538254946951², a number with with 675 divisors. At the scale of n = 28793728454807430335484², most squares m² are such that 3 | τ(m²), hence this is not precisely the start of flare phase (VII).
This number a(n) should be followed by a(n+1) = u = A37(2419960) = 2421516, at which point we commence flare phase (VII).
Table 3: Definition of phases in A350150 in terms of index n.
Flare Phases:
(I) 18.....19
(II) 54.....61
(III) 144....169
(IV) 686....849
(V) 11664..15515
(VI) 3543122..(n ≈ 5955320)
(VII)
(n ≈ 5.7587 × 1022 ...)
...
Regular Phases:
(i) 1.....17
(ii) 20.....53
(iii) 62....143
(iv) 170....685
(v) 850..11663
(vi) 15516..3543121
(vii) (n ≈ 4839917..5.7587 × 1022)
...
Regular phases.
We have shown that regular phases, i.e., α-control, skip m² that have already appeared, whereas k ∈ A37 with τ(k) in a “shallow totient class”, including k : 6 | k, go missing. Trajectory α consists of square m² : 3 | τ(m²), hence trajectory β denies k : 3 | τ(k). Early on in the sequence a, this concerns τ(k) = 6. We see this is merely the initial manifestation of a crucial feature of the regular phase. See Theorem 3.2 and Observation 3.3.
A hallmark of regular phases (outside of the first) is the maintenance in α of τ(k) ≡ 0 (mod 3). That is, the square k in a regular phase have τ(k) such that 3 | τ(k). The last square in the regular phase has a number of divisors that is not divisible by 3, which precipitates a flare phase.
Recall sequence Mα such that Mα(n) = τ(a(2n+1)) mod 3. This sequence begins:
1, 0, 0, 2, 0, 0, 0, 1, 2, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 1, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 1, 2, 2, 1, 2, 1, 2, 1, 1, 2, 2, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...
We find that, aside from regular phase (i) = a(1..17), hence for n > 17, regular phases correspond to a(2n−1) = k : k ∈ α ∧ 3 | τ(k) and the first occasion of k : k ∈ α ∧ τ(k) ≠ 0 (mod 3), and flare phases correspond to k : k ∈ α ∧ τ(k) ≠ 0 (mod 3). See Theorem 3.4.
Flare phases.
Flare phases or phases of β-control interrupt more-or-less increasing regular nature of trajectories α and β among squares and nonsquares, respectively. The general behavior of the sequence in α-control is nearly incrementation of i for α = a(2n+1) = A290(i), and for β = a(2n) = A37(i). In a flare, α increases markedly faster, and β falls to finally incorporate the persistent unused term u. As stated, flare phases involve odd-indexed a(2n−1) = k : k ∈ α ∧ τ(k) ≠ 0 (mod 3). See Theorem 3.5.
Let m = τ(k). As a consequence of the influence of the trinality of τ(a(2n−1)), the fact that 3 | τ(a(2n−1)), m in regular phases is nontrine except the last square in the phase. This final square in a regular phase permits the entry of nonsquare k : 3 | τ(k). The succeeding square k is forced into τ(k) indivisible by 3, which admits another missing term k : 3 | τ(k) until cure, when we have k : 3 | τ(k) ∧ k > u. Since a smaller number u : gcd(u, τ( j)) is available, we no longer are in the mode of admitting k : 3 | τ(k) until we admit a square j : 3 | τ( j). The following tables examine the values m = τ(k) in regular and flare phases.
Table 4.1: τ(k) for k = a(2n+2) in regular phase (iv), corresponding to negative terms D(n) : 85 < n < 343.
regular phase iv : 3..6 distinct
m A067255(m) c(m)
--------------------
10 1.1 1
(12 21 1)
14 1..1 1
20 2.1 2
Table 4.2: τ(k) for k = a(2n+2) in regular phase (v), corresponding to negative terms D(n) : 425 < n < 5832.
regular phase v : 8..81 distinct
m A067255(m) c(m)
--------------------
10 1.1 29
14 1..1 3
(18 12 1)
20 2.1 31
28 2..1 3
40 3.1 8
Table 4.3: τ(k) for k = a(2n+2) in flare phase (V), corresponding to negative terms D(n) : 5832 ≤ n ≤ 7759.
flare phase V : 82..115 distinct
m A067255(m) c(m)
--------------------
18 12 1
30 111 31
42 11.1 1
60 211 1
Table 4.4: τ(k) for k = a(2n+2) in regular phase (vi), corresponding to negative terms D(n) : 7759 < n < 360000*.
* The upper limit represents the end of data and not the regular phase.
regular phase vi : 116...
m A067255(m) c(m)*
-------------------
10 1.1 404
14 1..1 33
20 2.1 699
28 2..1 47
40 3.1 317
50 1.2 11
56 3..1 19
70 1.11 3
80 4.1 57
100 2.2 3
112 4..1 1
160 5.1 1
Furthermore, in flare phases, we find that √a(2n−1) ∈ A1694. This stands to reason given 3 | τ(a(2n−1)) for a(2n−1) in flare phases, and as a consequence of the formula of τ(n) given standard form prime decomposition:
For n = ∏ pε,
τ(n) = ∏ (ε + 1).
In order to guarantee odd τ(n), all prime power factors must have even ε > 1, hence n a perfect square. Therefore, in flare phases, odd-indexed terms k = m² : m ∈ A1694 so as to bring in least unused u : 3 | τ(u) until we exhaust skipped u. The occasion m ∈ A1694 is necessary but insufficient, since we have squared primes p² in A1694, and these have 3 | τ(p²). Only m² : m that are prime q : gcd(q, a(2n)) = 1, or τ(a(2n))-rough values m admit persistent missing u. The gaps u are filled until exhausted, because k → m² on account of coprimality of number of divisors. (See Theorem 5.1).
Therefore, the emergence of m² : 3 | τ(m²) in trajectory α follows β-cure that serves as a toggle, and β-cure returns the sequence to regularity. (See supplemental definitions).
Thoughts on efficient computation.
One of the simplest codes to write begins thus:
Nest[Block[{a = #, k = 2, j = DivisorSigma[0, #[[-1]]]},
While[Nand[FreeQ[a, k], GCD[j, DivisorSigma[0, k]] == 1], k++];
Append[a, k]] &, {1}, 120]
This code relies on incrementing k starting from a fixed value and doesn’t account for the bifurcation of the sequence via [ 2 | τ(a(n)) ], therefore it takes a minute to generate 28 terms. Installation of a register system to signify whether a term k is in a, and a record of the least unused u help somewhat. Selecting only squares for odd terms and nonsquares for even-indexed terms is very helpful, especially if there is a separate tracking for the least unused square v = m². Finally, memoization of A37, A5* A37, A1694, and A5* A1694 eliminate repetitive calculations of τ(k). We thus arrive at Code 1, which requires about 1700 s to generate 214 terms, including flare phase (V).
Since the draft of this paper, we have added a toggle-sensing variable that records a(2n) = A37(i) when τ(a(2n+1)) mod 3 ≡ ±1 during α-control. The code exploits Theorem 3.5. This sets the program in β-control mode, looking only at m ∈ A1694 for m² in α. The toggle looks for β-cure, i.e., when a(2n+2j) > a(2n) to reset α-control. It requires about an hour to generate 214 terms, including flare phase (V). This code requires about as much time to generate 214 terms, including flare phase (V).
Having additionally memoized a sufficient number of terms in h, and recognizing α-control may ignore persistent least unused u in favor of a local minimum, we suspect that optimization will streamline generation of the sequence so as to obtain something on the order of 220 terms. The goal would certainly involve reaching at least 3520000 terms so as to obtain data on flare phase (VI).
This program would need to track persistent u throughout, but a local minimum t = u at the outset of β-cure. This would eliminate walking up from u to find k ∈ A37 during α-control. Using least unused w = h(i) and incrementing i during β-control would further shorten generation time. These methods rely on memoizing h and A5* h in sufficient numbers to handle generation of flare phase (VI). We have 220 terms of h and seek about 223 terms of A350150.
Implementation of h(w) reduced generation time of 214 terms, including flare phase (V) to 28.8 s. Using a constant d = 27, we increment k from a(2n−2) − d in α-control and generate 218 terms in as many seconds. Ultimately the enhanced method based on Theorem 5 et al. yielded 3.6 million terms in about 15 minutes.
Theorems.
We restate the axioms:
Axiom 1. The coprimality directive: a(n+1) = k : τ(j) ⊥ τ(k).
Axiom 2. The inequality directive: k ∉ a(1..n−1), ∴ j ≠ k.
Axiom 3. The greedy directive: Let k : τ(j) ⊥ τ(k) and let k' : τ(j) ⊥ τ(k' ) ∧ k < k'. a(n+1) = k.
Axiom 4. a(n) is nonnegative.
Typically we presume axioms 2 and 4 apply to any proposition.
Sycamore noted the following in the comments of A350150:
A permutation of the positive integers. Identical to A137442 until a(18), with some terms in common thereafter. Numbers with the same number of divisors appear in their natural order, e.g. primes; τ(p) = 2, odd squarefree semiprimes; τ(p × q) = 4, etc.
His argument follows from the definition of A137442.
Let u be the smallest missing number in A350150, a consequence of the greedy axiom. Let trajectory α include early terms and let trajectory β include late terms, per scatterplot. Generally, m² : τ(m²) is odd appear in α = a(2n−1) and k ∈ A37 : 2 | τ(k) appear in β = a(2n). The objective is to prove the trajectories observed in scatterplot align with observation. This is tantamount to proving that we have intercalated or alternating square and nonsquare terms in A350150. Let h = A350014 = m ∈ A1694 : τ(m²) ⊥ 3, tantamount to m : τ(m²) ≡ ±1 (mod 6), implying h ⊂ A1694. We also define v as the least missing square, and w as the least missing number m² : m ∈ h.
Observations in an exceptional first 18 terms of A350150:
τ(m²)
1 3 3 5 3 9 3 7 5 5 9
a(2n+1) 1² (2²) (3²) 4² (5²) (6²) (7²) 8² 9² 25² (10²) ...
a(2n) 1⊠ 2⊠ 3⊠ 4⊠ 5⊠ 6⊠ 7⊠ 8⊠ (9⊠) 10⊠ ...
2 2 2 4 2 4 4 2 6 2
τ(k)
The first 17 terms of the sequence feature odd-indexed squares (i.e., m² in α) that may or may not present divisibility by 3 with no effect on the even-indexed nonsquare terms (i.e., k in β).
Table 2.1 places the first odd indexed (α) terms, stated as m² above and intercalated with even indexed (β) terms, stated as k ∈ A37 (denoted by ⊠) above.
Though there was an opening for 3 | τ(k) in β in the wake of a(7) = 4², u = A37(4), and so a(8) = A37(4) = 6. It is fortunate that A37(9) = 12 = a(18) could enter the sequence “as expected”, that is, in order of A37, as τ(a(17)) = τ(9²) = 5. These are special cases.
Until a(18) = 12, we have only seen k : τ(k) mod 3 ≡ ±1 in β. Thereafter, given 3 | τ(m²) in α, we are forced into k : τ(k) mod 3 ≡ ±1. Consequently, nonsquares 18, 20, 28, and 32 are delayed in entering β until after the appearance of τ(m²) mod 3 ≡ ±1 in α at a(53) = 729 = 36. Thereafter we finally have a(54) = 18.
Theorem 1. Nonsquare k may not occur adjacently.
Lemma 1. If prime q | τ(a(n)) then q ⊥ τ(a(n+1)), a consequence of the coprimality and inequality axioms.
Proof 1. Given Lemma 1, if 2 | τ(a(n)) then 2 ⊥ τ(a(n+1)). The divisor counting function is odd iff τ(m²) : A290(m) = m², since the multiplicative complements m × m = m² count as a single distinct divisor. Conversely, k : 2 | τ(k) have nonsquare k ∈ A37. Therefore adjacent nonsquare k such that 2 | τ(k) does not occur in A350150. ∎
Proposition 2. a(2n−1) = m² ∧ a(2n) = k ∈ A37. In other words, A350150 is bifurcated into odd-indexed terms that are square, and even-indexed terms that are nonsquare.
In order to prove this, we need other theorems. Essentially, we need to show that the least missing number u is always nonsquare. If we have square u, then we will have adjacent squares iff a(n) ⊥ u. For example, if τ(a(n)) = 5 × 7 ∧ τ(u) = 3, then a(n+1) = u, by definition of least missing number u, and ultimately as a consequence of the greedy axiom.
Theorem 3.1. 3 | τ(a(n)) toggles between a phase of “α-control” and “β-control”. In other words, supposing Proposition 1.2 is true, if 3 | τ(m²), then 3 ⊥ τ(k), and if 3 | τ(k), then 3 ⊥ τ(m²).
Proof 3.1. Given Lemma 1, we know that if 3 | τ(a(n)), then 3 ⊥ τ(a(n+1)). Hence, so long as every other term has tau divisible by 3, the intercalated terms may not have tau divisible by 3. In other words, if 3 | τ(a(2n−1)), then 3 ⊥ τ(a(2n)) via induction. The converse is also possible, but let us for the moment consider only this case, so as to suppose Proposition 2 is true. Hence we have a(2n−1) in a trajectory of early terms α, and a(2n) in a trajectory of late terms β, such that Whereupon we have 3 ⊥ τ(a(2n−1)), then if u : 3 | τ(u), through the greedy axiom, a(2n) = u and 3| τ(a(2n)). Thereafter, since 3 | τ(a(2n)), 3 ⊥ τ(a(2n−1)) via induction, until 3 ⊥ u. This permits 3 | τ(a(2n−1)) ∧ 3 ⊥ τ(a(2n)) until we have 3 ⊥ τ(a(2n−1)), etc., an alternating pair of phases. ∎
Clearly, these alternating phases emerge regardless of parity of index, so long as one trajectory consists of numbers that draw from the smallest missing number u and the other trajectory includes terms that appear early.
Theorem 3.2. For 1 ≤ n ≤ 18, while q | τ(m²) ∧ (u : q | τ(u) ∧ u ∈ A37), the entry of squares and nonsquares, respectively, occurs in order. This is to say, a(2n) = A37(i), a(2n+2) = A37( j), j = i + 1, as n increases, and a(2n−1) = m², a(2n+1) = (m')², m' = m + 1, as n increases.
Proof 3.2. Direct consequence of Lemma 1. ∎
Observation 3.3. The appearance of a(18) = 12, τ(12) = 6 denies a(19) = 10², τ(10²) = 9. Instead, a(19) = 25², τ(25²) = 5. This is the first conflict between terms and candidates. This is a consequence of the coprimality and greedy axioms. Because 25² appears early, it is depleted from the ensuing α-control phase, extending it.
Theorem 3.4 (α-control). Suppose a(2n−1) > a(2n) for n > 2. A sustained run of a(2n−1) : 3 | τ(a(2n−1)) delays admission of a(2n) : 3 | τ(a(2n)).
Proof 3.4. Direct consequence of Lemma 1 and the greedy axiom. As a result, u pertains to a(2n). ∎
Theorem 3.5 (β-control). Suppose a(2n−1) > a(2n) for n > 2, and let K be the smallest k denied entry during α-control. The emergence of 3 ⊥ τ(a(2n−1)) triggers a run of admissions of k : 3 | τ(k) into a(2n) and delays 3 | τ(a(2n−1)) until a(2n) = k' : k > K.
Proof 3.4. Direct consequence of Lemma 1 and the greedy axiom. As a result, u pertains to a(2n), since only a particular kind of m² could appear in β-control. Hence these m² appeared relatively early and are all larger than m² before the emergence of 3 ⊥ τ(a(2n−1)) as a consequence of greedy axiom. ∎
Theorem 4. q | τ(k) : q > 3 only foments a modest delay in the appearance of k in the sequence, regardless of whether or not k is prime or square.
Proof Sketch 4. Consequences of the inequality, coprimality, and greedy axioms. Since 2 and 3 are the commonest prime divisors as they are the smallest primes, The emergence of divisibility by 5, 7, etc. are rare and therefore interference or conflict with a term with an index of opposite parity is less likely, inversely proportional to the magnitude of q. (This is not a rigorous proof). ∎
Theorem 5.1. During β-control, i.e., given a(n) = k ∈ A37 : 3 | τ(k), a(n+1) in α is forced into m² : τ(m²) ≡ ±1 (mod 6).
Proof 5.1. Consequence of coprimality axiom and the nature of squares in Proof 1. Squares m² : τ(m²) is odd, hence, ∀m, τ(m²) belongs to ±1 ∨ 3 (mod 6). Since a(n) ⊥ a(n+1), we cannot have m : τ(m²) ≡ 3 (mod 6). Therefore we are left with m : τ(m²) ≡ ±1 (mod 6), a proper subset of A1694 (the powerful numbers). ∎
Theorem 5.2. 3 | τ(m²) is common while τ(m²) ≡ ±1 (mod 6) is rare as m increases.
Proof 5.2. τ(m²) is odd, hence τ(m²) belongs to {±1, 3} (mod 6). We might look to the densities of the prime-squares p² as τ(p²) = 3, and those of the squarefree semiprimes (pq)², as τ(p²q²) = 9, etc., amid the natural numbers. We see that τ(n) = q prime only for prime power p(q−1), a consequence of the formula for τ(n) given standard form prime decomposition n = ∏ pε, τ(n) = ∏ (ε+1). Therefore, p(q−1) : q > 3 yields τ(p(q−1)) ≡ ±1 (mod 6), as τ(p(q−1)) is an odd prime q. We observe a(57) = 1296 = 36² = h(8)² is the first m² in A350150 with composite τ(m²) = 25 = +1 (mod 6), entering during β-control. Therefore, indeed, we are interested in m : τ(m²) ≡ ±1 (mod 6) rather than only p(q−1) : q > 3, a subset; i.e., A051676 ⊂ A350014. We submit that 3 is the smallest odd prime, and that divisibility by q : q > 3 is rarer than that of divisibility by 3. The numbers m : τ(m²) ≡ ±1 (mod 6) appear as a subset of m² : m ∈ A1694 (the powerful numbers), which is in turn a subset of squares, i.e., A051676 ⊂ A350014 ⊂ A1694. ∎
The first 18 terms are exceptional in that the appearance of several “windows of opportunity”, that is, the occasion of 3 ⊥ τ(a(2n−1)) did not usher in 3 | τ(a(2n)) because the least missing number u was not divisible by 3. All nonsquares that could enter did enter on schedule. After a(18), we see delayed entry, since 3 | τ(a(2n−1)) rarifies as n increases, but also because 3 ⊥ τ(a(2n−1)) occurs even earlier in a distinct β-control phase after a(63), depleting the occasion of 3 | τ(a(2n−1)) until some m² > (m')² that appeared in a previous β-control phase.
Theorem 6. Least missing number u(n) is nonsquare for n > 0.
Proof 6. The sequence of squares, A290(m) = m² grows faster than that of nonsquares, A37. Given Theorems 1, 3.1, 3.4, 3.5, 4, and 5, we see that u(n) is nonsquare for n > 0. ∎
Now we return to Proposition 2, stating it in a different way:
Theorem 2. A350150 is comprised of an α trajectory consisting of a(2n−1) = m² and a β trajectory consisting of a(2n) = k ∈ A37.
Proof 2. Direct consequence of Theorems 1 and 6; tantamount to Proposition 2. ∎
Let us call the emergence of 3 ⊥ τ(a(2n−1)) the β-control trigger, since it allows any u : 3 | τ(u) to appear and usher in β-control. Define a(α1) = m² : 3 ⊥ τ(m²), the last square in outgoing α-control, and a(α0) = (m')² : m' = m + 1, the first square in a new phase of α-control. Then index β0 = α_1 + 1 and a(β0) = u : 3 | τ(u), the first nonsquare in β-control. Also, let β2 =β0− 2 with a(β_2) = A37(i). We see a(β0) = A37( j) : i > j. Therefore, a(β1) = A37(i+1), the last nonsquare in outgoing β-control, i.e., β-cure.
Corollary 2.1: There exists a least missing square v(n) > u(n) for n > 0.
Proof 2.1: Consequence of Theorem 2, and ultimately the coprimality and greedy axioms. ∎
Corollary 2.2: There exists a least missing m² : m ∈ h, w(n) ≥ v(n) for n > 0 that enters the sequence either in β-control or serves as the β-control trigger ending α-control.
Proof 2.2: For a(n) : α1 < n < α0, we have m² : m ∈ h, i.e., m² : τ(m²) ≡ ±1 (mod 6), which is the entry of w = h( j)² into a, unless (τ(h( j)²), τ(a(2n))) = q : q > 3, wherein we may instead have h( j+1)², and in due course h( j)² whereupon (τ(h( j)²), τ(a(2n))) = 1. If h( j)² fails to enter a in the current phase of β-control, it will become a(α1) in a new phase of α-control, ending that α-control phase and triggering a new phase of β-control. This is because m² is restricted to m² : m ∈ h, i.e., m² : τ(m²) ≡ ±1 (mod 6) as the preceding term k is such that 3 | τ(k), and by the greedy axiom generally consumes terms in h sequentially. ∎
Theorems 3.4 and 3.5 represent the delay of k ∈ A37 : 3 | τ(k) until β-control trigger. All of these k appear during β-control until β-cure. Then we enter α-control. Per Theorem 4, conflicts between α and β regarding q > 3 prove inconsequential regarding both square-nonsquare bifurcation and alternating α-control and β-control phases.
The existence of u, v, and w enables an expedited code (see Code 6) that exploits these least missing numbers given index parity (as regards the first 2) and the signal toggled on by β-control trigger (which ushers in β-control) and β-cure (which, provided 3 ⊥ τ(k), ushers in α-control, in the negatory case, merely prolongs β-control until 3 ⊥ τ(k) eventually materializes.)
Summary. Therefore we may say that A350150 is bifurcated into two intercalated trajectories, an early or α trajectory of squares, and a β or late trajectory of nonsquares. Additionally, A350150 exhibits alternating phases governed by divisibility of τ(a(n)) by 3. The emergence of a relatively rare m² : τ(m²) ≡ ±1 (mod 6) instigates a flare phase of β-control wherein terms m² in α are forced into m ∈ A350014. Whereupon we have 3 ⊥ τ(k) : k ∈ A37, that is, in trajectory β, we exit the flare phase and begin a new regular phase of α-control.
Conclusion.
We have described the bifurcation of A350150 = a into 2 intercalated trajectories. Trajectory α includes odd-indexed terms a(2n−1) = k : √k ∈ ℕ, i.e., k ∈ A290, as a consequence, τ(k) ≡ 1 (mod 2). Trajectory β includes even-indexed terms a(2n) = k : √k ∉ ℕ, i.e., k ∈ A37, as a consequence, 2 | τ(k). These trajectories generally proceed such that a(2n) < a(2n+2), a(2n) = A37(i) ∧ a(2n+2) = A37(i+1) in β, and a(2n−1) < a(2n+1), a(2n−1) = m² ∧ a(2n+1) = (m+1)² in α. We call this the “regular phase” or behavior of the sequence a.
There are clearly 2 distinct phases observed in a as shown by log-log scatterplot (Figure 2). Indeed there is a regular phase for n > 17 characterized principally by a(2n−1) = k : k ∈ α ∧ 3 | τ(k) and the first occasion of k : k ∈ α ∧ τ(k) ≠ 0 (mod 3), and flare phases correspond to k : k ∈ α ∧ τ(k) ≠ 0 (mod 3). We have detailed the phases observed in the dataset. We have shown that √a(2n−1) ∈ A1694 in flare phases so as to furnish square k : 3 | τ(k)
For n > 17, the sequence toggles between a regular or α-control phase, and a flare or β-control phase. (Theorem 3.1 et al.)
At the outset, α is in the driver seat; we have squares a(2n−1) = m² = A290(i)² : 3 | τ(m²) that enter according to i++, skipping extant k. Meanwhile, β admits nonsquare k = A37( j) roughly according to j++, prefering τ(k) = 2ε : ε > 0. This is because m² implies 2 ∤ τ(m²), yet any odd value qualifies, and prime m = p, p², etc., throw 3 | τ(m²). As a result, u : τ(u) ≡ 0 (mod 6) are skipped and comprise gaps in nonsquare admission, the least of which becomes a persistent least unused u. This “regular phase” persists so long as 3 | τ(m²), which subtends for most m. (Theorem 3.4)
Whereupon we have 3 ∤ τ(m²) for some m ∈ A1694, we admit the persistent least unused u. This toggles the sequence into a “flare phase” and puts β in control. (Theorem 3.5)
Now we have 3 | τ(k) and the regular 3 | τ(m²) is not allowed. Instead, m is forced into A1694 (a necessary but insufficient condition), but more precisely, into h = A350014 (Theorem 5.1). The gaps k in admission of nonsquares are consumed as they have the property q | τ(k) : q odd and prime. Consequently, m is forced such that 2q ∤ τ(m²), etc., until all gaps are filled and β cures, meaning that k = A37(j+1). Chance is good that 6 ∤ A37(j+1), allowing 3 | τ(m²), which toggles the sequence back into a regular phase. If 6 | A37(j+1), then such is skipped and A37(j+2) chosen instead, while A37(j+1) = u persistent, and will have to wait till 3 ∤ τ(m²).
This concludes our examination..
Appendix.
Table A: Examination of differences in the indices j of A37( j) = a(2n), covering all instances of rebasing β up to the beginning of flare phase (IV).
Differences in T tau(k)
i D(i-1) D(i) D(i+1) n a(n-2) a(n) a(n+2) n-2 n-1 n n+1 n+2
---------------------------------------------------------------------
D(26) 1 -16 2 a(52) 34 35 18 4 9 4 7 6
D(71) 2 -46 1 a(142) 91 93 44 4 3 4 35 6
D(135) 2 -3 4 a(270) 163 165 162 2 45 8 3 10
D(251) 2 -1 2 a(502) 319 321 320 4 21 4 9 14
D(263) 2 -1 3 a(526) 335 337 336 4 15 2 9 20
D(333) 1 -2 3 a(666) 433 434 432 2 15 8 9 20
D(342) 2 -337 2 a(684) 443 445 96 2 45 4 7 12
D(531) 2 -1 2 a(1062) 591 593 592 4 15 2 9 10
D(556) 1 -2 4 a(1112) 626 627 624 4 15 8 9 20
D(615) 2 -1 2 a(1230) 703 705 704 4 105 8 3 14
D(647) 2 -1 2 a(1294) 751 753 752 2 45 4 9 10
D(765) 2 -1 2 a(1530) 911 913 912 2 45 4 9 20
D(788) 2 -1 2 a(1576) 943 945 944 4 15 16 9 10
D(800) 2 -1 4 a(1600) 959 962 960 4 63 8 27 28
D(867) 3 -1 2 a(1734) 1051 1054 1053 2 15 8 3 10
D(903) 2 -1 2 a(1806) 1103 1105 1104 2 15 8 27 20
D(1021) 2 -1 2 a(2042) 1263 1265 1264 4 45 8 9 10
D(1079) 2 -1 2 a(2158) 1343 1345 1344 4 21 4 15 28
D(1160) 2 -1 2 a(2320) 1455 1457 1456 8 45 4 9 20
D(1209) 3 -1 2 a(2418) 1518 1522 1520 16 45 4 9 20
D(1280) 3 -2 3 a(2560) 1615 1618 1616 8 45 4 27 10
D(1327) 5 -4 5 a(2654) 1679 1685 1680 4 15 4 21 40
D(1602) 2 -1 2 a(3204) 2063 2065 2064 2 45 8 27 20
D(1626) 3 -2 3 a(3252) 2095 2098 2096 4 75 4 21 10
D(1864) 2 -1 2 a(3728) 2415 2417 2416 16 45 2 9 10
D(1956) 2 -1 2 a(3912) 2543 2545 2544 2 45 4 21 20
D(1981) 1 -2 3 a(3962) 2577 2578 2576 4 45 4 9 20
D(2051) 3 -2 5 a(4102) 2671 2674 2672 2 15 8 21 10
D(2354) 3 -1 2 a(4708) 3086 3089 3088 4 45 2 9 10
D(2423) 3 -2 3 a(4846) 3183 3186 3184 4 45 16 9 10
D(2463) 2 -1 2 a(4926) 3239 3241 3240 4 15 4 9 40
D(2470) 2 -1 2 a(4940) 3247 3250 3248 4 45 16 9 20
D(2576) 3 -2 3 a(5152) 3391 3394 3392 2 63 4 3 14
D(2683) 1 -2 3 a(5366) 3537 3538 3536 8 105 8 3 20
D(2705) 2 -1 2 a(5410) 3567 3569 3568 8 45 4 9 10
D(2764) 2 -1 3 a(5528) 3647 3649 3648 4 63 4 3 28
D(2799) 2 -1 3 a(5598) 3695 3697 3696 4 15 2 27 40
D(3192) 2 -1 2 a(6384) 4239 4241 4240 8 45 2 27 20
D(3216) 2 -1 2 a(6432) 4271 4273 4272 2 15 2 9 20
D(3264) 3 -1 3 a(6528) 4334 4337 4336 8 15 2 27 10
D(3287) 2 -1 2 a(6574) 4367 4369 4368 4 45 4 9 40
D(3351) 2 -1 2 a(6702) 4454 4456 4455 8 45 8 9 20
D(3405) 3 -1 2 a(6810) 4526 4529 4528 8 45 4 27 10
D(3412) 2 -1 2 a(6824) 4535 4537 4536 4 75 4 3 40
D(3753) 2 -1 2 a(7506) 4999 5001 5000 2 45 4 3 20
D(3944) 3 -2 1 a(7888) 5263 5266 5264 4 15 4 27 20
D(3967) 2 -1 2 a(7934) 5295 5297 5296 8 135 2 9 10
D(3979) 2 -1 2 a(7958) 5311 5313 5312 4 315 16 9 14
D(4036) 4 -1 2 a(8072) 5389 5393 5392 4 45 2 3 10
D(4059) 3 -2 3 a(8118) 5423 5426 5424 8 15 4 27 20
D(4211) 2 -1 5 a(8422) 5631 5633 5632 4 45 4 9 20
D(4246) 3 -1 2 a(8492) 5678 5681 5680 8 135 8 3 20
D(4299) 2 -1 2 a(8598) 5750 5752 5751 16 225 8 9 10
D(4363) 3 -2 3 a(8726) 5839 5842 5840 2 15 8 3 20
D(4388) 2 -1 2 a(8776) 5871 5873 5872 8 45 4 27 10
D(4418) 2 -1 4 a(8836) 5912 5914 5913 8 45 4 9 10
D(4434) 1 -3 5 a(8868) 5938 5939 5936 4 135 2 3 20
D(4505) 1 -2 3 a(9010) 6033 6034 6032 4 15 8 3 20
D(4528) 2 -1 3 a(9056) 6063 6065 6064 8 15 4 3 10
D(4552) 2 -1 2 a(9104) 6095 6097 6096 8 45 8 9 20
D(4599) 2 -1 2 a(9198) 6159 6161 6160 4 45 4 9 40
D(4646) 1 -3 5 a(9292) 6226 6227 6224 8 45 4 3 10
D(4690) 2 -1 2 a(9380) 6287 6289 6288 2 315 4 9 20
D(4784) 3 -2 5 a(9568) 6415 6418 6416 4 15 4 63 10
D(4806) 2 -1 3 a(9612) 6447 6449 6448 8 45 2 9 20
D(4901) 3 -1 2 a(9802) 6574 6577 6576 8 15 2 27 20
D(5011) 3 -2 5 a(10022) 6722 6726 6723 4 75 16 81 10
D(5020) 1 -2 3 a(10040) 6737 6738 6736 2 15 8 27 10
D(5156) 4 -3 5 a(10312) 6927 6931 6928 4 45 4 27 10
D(5181) 2 -1 2 a(10362) 6965 6967 6966 8 75 2 21 20
D(5202) 2 -1 2 a(10404) 6991 6993 6992 2 45 16 3 20
D(5344) 1 -2 3 a(10688) 7185 7186 7184 8 15 4 9 10
D(5359) 1 -3 4 a(10718) 7205 7206 7203 8 45 8 9 10
D(5394) 1 -2 3 a(10788) 7249 7250 7248 4 15 16 27 20
D(5416) 3 -2 3 a(10832) 7279 7282 7280 4 45 8 21 40
D(5492) 1 -3 6 a(10984) 7378 7379 7376 16 15 4 9 10
D(5556) 2 -1 2 a(11112) 7471 7473 7472 4 45 8 3 10
D(5580) 2 -1 2 a(11160) 7503 7505 7504 8 225 8 3 20
D(5628) 2 -1 2 a(11256) 7567 7570 7568 8 135 8 9 20
D(5661) 1 -2 3 a(11322) 7615 7616 7614 4 45 28 27 20
D(5746) 2 -1 2 a(11492) 7727 7729 7728 2 45 4 9 40
D(5831) 2 -7328 2 a(11662) 7843 7845 450 8 21 8 91 18
...
Table B: Milestones in A350150:
This chart summarizes toggling between α-control and β-control via 3 | τ(a(n)):
n a(n) τ(a(n)) α: m² ∨ β: k ∈ A37
---------------------------------------------------------------------
16 11 2 8 ⊠
18*β 12 6 9 ⊠
20 13 2 10 ⊠
(I)
17 81 5 9² h(4)² = A1694(4)²
19*α 625 5 25² h(5)² = A1694(6)²
21 100 9 10²
52 35 4 30 ⊠
54*β 18 6 14 ⊠
62 37 2 31 ⊠
(II)
53 729 7 27² h(6)² = A1694(7)²
61*α 4096 13 64² h(10)² = A1694(11)²
63 784 15 28²
142 93 4 84 ⊠
144*β 44 6 38 ⊠
170 94 4 85 ⊠
(III)
143 5184 35 72² h(11)² = A1694(12)²
169*α 83521 5 289² h(24)² = A1694(28)²
171 5329 3 73²
684 445 4 424 ⊠
686*β 96 12 87 ⊠
850 446 4 425 ⊠
(IV)
685 117649 7 343² h(25)² = A1694(30)²
849*α 29986576 25 5476² h(107)² = A1694(136)²
851 118336 21 344²
11662 7845 8 7757 ⊠
11664*β 450 18 429 ⊠
15516 7846 4 7758 ⊠
(V)
11663 34012224 91 5832² h(108)² = A1694(140)²
15515*α 3133342515625 175 1770125² h(2034)² = A1694(2713)²
15517 34023889 9 5833²
3543120 2421514 16 2419958 ⊠
3543122*β 7848 24 7760 ⊠
(4839918) (2421515) (4) (2419959 ⊠)
(VI)
3543121 3138428376721 13 1771561² h(2035)² = A1694(2714)²
(4839917)*α (134 × 316874)** (95) (169687148761²) h(650433)² = A1694(886993)²
(5.7587 × 10²²) > 28793728454807430335484²
**Decimal equivalent is 28793728454637743835121.
References:
[1] D. Suryanarayana and R. Sita Rama Chandra Rao, The distribution of square-full integers, Ark. Mat., Vol. 11, No. 1-2 (1973), 195-201. See Section 3.7.
Code A: Memoize 220 terms of A048691 and store in variable a048691:
Monitor[Do[Set[a048691[n], DivisorSigma[0, n^2]], {n, 2^20}], n];
Code 1: Efficiently generate a and store it in the variable a350150, requires Code A.
a350150 = Block[{s = {1}, c, j, k, m, u = 1, v = 1}, c[_] = 0;
Do[Set[c[s[[i]]], i], {i, Length[s]}]; j = Last[s];
m = DivisorSigma[0, j]; While[c[u] > 0, u++];
While[c[v^2] > 0, v++]; s~Join~Reap[Monitor[Do[
If[j == u, While[c[u] > 0, u++]] (* calibrate least unused u *);
If[j == v^2, While[c[v^2] > 0, v++]] (* calibrate least unused v *);
If[v >= 2^24, Break[]];
If[OddQ[i], Set[k, v];
While[Nand[c[k^2] == 0, GCD[m, a048691[k]] == 1], k++];
Set[k, k^2],
Set[k, u];
While[Nand[c[k] == 0, GCD[m, DivisorSigma[0, k]] == 1], k++]];
Sow[k]; Set[c[k], i]; Set[m, DivisorSigma[0, k]];
j = k, {i, Length[s] + 1, 2^14}], i]][[-1, -1]]]
Code 2: Generate auxiliary sequences d(n) = τ(a(n)), u(n) = least unused number, r = maxima, s = local minima.
a350150d = DivisorSigma[0, a350150];
a350150u = Block[{u = 1, c, s = a350150}, c[_] = 0;
Reap[Do[Set[c[s[[i]]], i]; If[s[[i]] == u, While[c[u] > 0, u++]];
Sow[u], {i, Length@s}]][[-1, -1]]];
a350150r = Union@ FoldList[Max, a350150];
a350150s = Union@ a350150u;
Code 3: Compute A37, find T = j : a(2n) = A37( j), and D = first differences of T.
a000037 = Complement[Range[2^#], Range[2^(#/2)]^2] &[20];
a350150tt = With[{s = TakeWhile[a000037, # <= 176591 &]},
Table[FirstPosition[s, a350150[[2 n]]][[1]], {n, Length[a350150]/2}] ];
a350150dd =
Differences@ a350150tt;
Block[{nn = 20000, r, s, t, u, out = -120},
s = a350150[[1 ;; nn]];
r = Array[If[FreeQ[a350150r, #], out, #] &@ s[[#]] &, nn];
t = Array[If[FreeQ[a350150s, #], out, #] &@ s[[#]] &, nn];
u = a350150u[[1 ;; nn]];
ListPlot[{s, r, t, u,
Array[Labeled[#, #, Top] &@s[[#]] &, 24];
Array[If[MemberQ[{19, 61, 169, 849, 15515}, #],
Labeled[#, #, Top, LabelStyle -> Red] &@ s[[#]], out] &, nn],
Array[If[MemberQ[{17, 53, 143, 685, 11663}, #],
Labeled[#, #, Bottom, LabelStyle -> Red] &@ s[[#]], out] &, nn],
Array[If[MemberQ[{18, 54, 144, 686, 11664}, #],
Labeled[#, #, Bottom, LabelStyle -> Blue] &@ s[[#]], out] &, nn],
Array[If[MemberQ[{62, 170, 850, 15516} - 2, #],
Labeled[#, #, Top, LabelStyle -> Blue] &@ s[[#]], out] &, nn]},
ImageSize -> 1440,
ScalingFunctions -> {"Log2", "Log2"},
PlotStyle -> {
Directive[Black, PointSize[Small]],
Directive[Red, PointSize[Medium]],
Directive[Blue, PointSize[Medium]],
Directive[Hue[1/7, 1, .875], PointSize[Tiny]],
Transparent, Transparent, Transparent, Transparent, Transparent} ] ]
Block[{nn = 2^9, kk = 16, d, s, t, u, out = -120},
d = a350150d[[2 ;; nn + 1]];
s = a350150[[1 ;; nn]];
t = Array[
If[And[PrimeNu[#] == 2, EvenQ[#]] &@ a350150d[[# - 1]], s[[#]], out] &, nn];
u = Array[
If[And[PrimeNu[#] == 2, EvenQ[#]] &@ a350150d[[#]], s[[#]], out] &, nn];
ListPlot[{s, Array[s[[#]] &, nn/kk],
s, t, u, {1}~Join~Most[d],
Array[Labeled[#, #, Top, LabelStyle -> Gray] &[s[[#]]] &, nn/kk],
Array[If[t[[#]] <= 0, out, Labeled[#, #, Top] &@ s[[#]]] &, nn/kk],
Array[Labeled[t[[#]], d[[# - 1]], Bottom, LabelStyle -> Red] &, nn],
Array[If[u[[#]] <= 0, out, Labeled[#, #, Top] &@ s[[#]]] &, nn],
Array[Labeled[u[[#]], d[[# - 1]], Bottom, LabelStyle -> Blue] &, nn]},
ImageSize -> 1440,
ScalingFunctions -> {"Log2", "Log2"},
Joined -> {False, True, False, False, False, True, False, False},
PlotStyle -> {
Directive[Black, PointSize[Tiny]],
Directive[Gray, PointSize[Tiny], Thin],
Directive[Black, PointSize[Small]],
Directive[Red, PointSize[Medium]],
Directive[Blue, PointSize[Medium]],
Directive[Green, PointSize[Tiny], Thin],
Transparent, Transparent, Transparent, Transparent, Transparent} ] ]
Code 6: Expedited code using α-β control toggle.
Preparation; memoize A1694, h and τ(h(n)) in about 3-5 minutes:
a1694 = Block[{nn = 2^47},
Union@ Flatten@
Monitor[Table[a^2*b^3, {b, nn^(1/3)}, {a, Sqrt[nn/b^3]}], b]]
(* This efficient script written 2014 0811 by Robert G. Wilson v at A001694 *);
a1694h = Select[a1694[[1 ;; 2^22]],
Mod[DivisorSigma[0, #^2], 3] != 0 &];
Monitor[Do[Set[h1694[i], a1694h[[i]]], {i, Length[a1694h]}], i];
Monitor[Do[Set[a1694hd[i], DivisorSigma[0, h1694[i]^2]], {i, Length[a1694h]}], i]
Main extensible routine; set s to a350150 and build on previous datasets:
a350150 = Block[{s = {1}, b = 0, c, d, j, k, m, t, u, v, w, z},
b = t = c[_] = 0;
u = v = w = z = 1;
Do[Set[c[s[[i]]], i], {i, Length[s]}];
j = Last[s]; d = DivisorSigma[0, j];
While[c[u] > 0, u++];
While[c[v^2] > 0, v++];
While[c[h1694[w]^2] > 0, w++];
s~Join~Reap[Monitor[Do[
If[j == u, While[c[u] > 0, u++]] (* calibrate least unused u *);
If[j == v^2, While[c[v^2] > 0, v++]] (* calibrate least unused v *);
If[j == h1694[w], While[c[h1694[w]^2] > 0, w++]] (* calibrate least unused w *);
If[v >= 2^24, Break[]];
Which[
And[OddQ[i], t > 0],
Set[k, w];
While[Nand[c[h1694[k]^2] == 0, GCD[d, a1694hd[k]] == 1], k++];
Set[k, h1694[k]^2],
OddQ[i],
Set[k, v];
While[Nand[c[k^2] == 0, GCD[d, a048691[k]] == 1], k++];
Set[k, k^2],
True,
If[And[i > 2^10, t == 0], Set[k, b - 2^8], Set[k, u]];
While[Nand[c[k] == 0, GCD[d, DivisorSigma[0, k]] == 1], k++]];
Sow[k];
Set[c[k], i];
Set[d, DivisorSigma[0, k]];
If[OddQ[i], Set[m, Mod[d, 3]], Set[b, k]];
Which[
And[OddQ@ i, i > 24, m != 0, t == 0], t = b,
And[EvenQ@ i, b > t, t > 0], t = 0,
True, Nothing] (* toggle *);
j = k, {i, Length[s] + 1, 2^20}], i]][[-1, -1]]]
(* Extensible Code with flare expedition *)
Concerns sequences:
A000005: The divisor counting function τ(n).
A000037: Nonsquare numbers.
A000290: Perfect squares.
A001694: Squareful numbers, numbers that are not squarefree.
A048691: Number of divisors of perfect squares.
A051676: Composite numbers whose square has a prime number of divisors.
A137442: n² followed by smallest integer not yet listed.
A350014: Sequence h : a(n) = { m : τ(m²) ≡ ±1 (mod 6) } i.e., { m : τ(m²) ⊥ 6 }.
A350150: Sequence a.
A352475: h²
= { m : τ(m) ≡ ±1 (mod 6) } i.e., { m : τ(m) ⊥ 6 }
A354799: { A1694 \ A350014 } = { m : τ(m²) ≡ 3 (mod 6) }.
Document Revision Record.
2021 1215 2200 Draft.
2021 1219 1200 Final.
2021 1223 2200 The governance of a by [ 2 | τ(a(n)) ] and [ 3 | τ(a(n)) ].
2021
1225 1700 Estimated flare and regular phases beyond dataset of 360000 terms.
2021 1225 2230 Code optimization.
2022 0116 1015 Updated phases, further optimized code.
2022 0119 1630 Theorems.
2022 0316 1915 Minor error clarified.