The Sisyphus Sequence
OEIS A350877, a sequence by Éric Angelini and Carole Dubois, this page written by Michael Thomas De Vlieger, St. Louis, Missouri, 2022 0121.
Abstract.
Analysis of A350877, a conditional self-referential sequence predicated on parity of the immediately preceding term.
Introduction.
Let a(1) = k = 1. If 2 | a(n), then a(n+1) = a(n)/2, else a(n+1) = a(n) × q : q = prime(k), in which case we increment k before proceeding to the next term. Hence we have a conditional function predicated on parity of input that consists of the immediately previous term.
The first terms of a follow:
1, 3, 6, 3, 8, 4, 2, 1, 8, 4, 2, 1, 12, 6, 3, 16, 8, 4, 2, 1, 18, 9, 28, 14, 7, 30, 15, 44, 22, 11, 42, 21, 58, 29, 70, 35, 78, 39, 86, 43, 96, 48, 24, 12, 6, 3, 62, 31, 92, 46, 23, 90, 45, 116, 58, 29, 102, 51, 130, 65, 148, 74, 37, 126, 63, 160, 80, 40, 20, 10, 5, 106, 53, 156, 78, 39, 146, 73, 182, 91, 204, 102, 51, 178, 89, 220, 110, 55, 192, 96, 48, 24, 12, 6, 3, 142, 71, 220, 110, 55, 206, 103, 260, 130, 65, 228, 114, 57, 224, 112, 56, 28, 14, 7, 180, 90, 45, 224, 112, 56, ...
Code 1 generates the sequence efficiently such that 224 terms can be generated in a couple minutes.
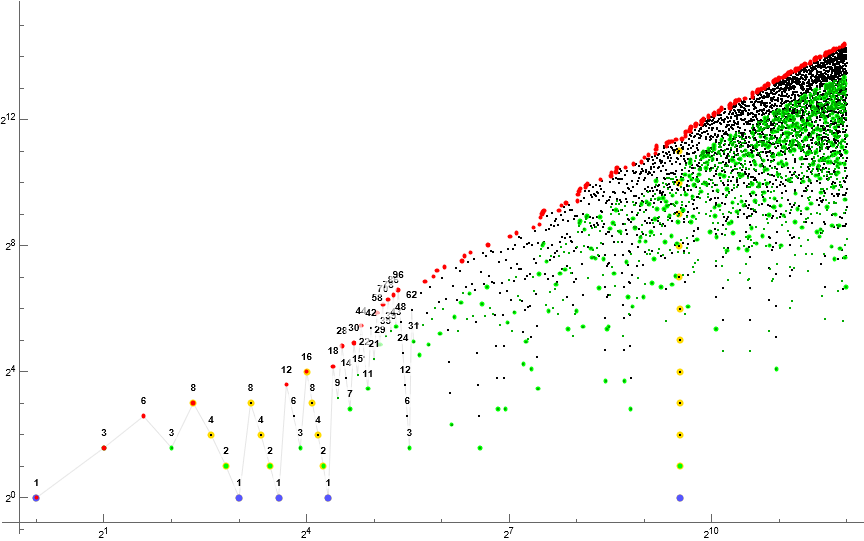
Figure 1: Scatterplot of a(n) for 1 ≤ n ≤ 210, showing records r in red, odd terms in green, prime terms with green emphasis, terms 2ε emphasized in gold, and 1’s in blue.
The most notable features of the scatterplot Figure 1 are bifurcation of even- and odd-indexed terms, and “flare” phases that happen approximately in a sort of exponential fashion.
Auxiliary sequences.
Define sequence d(n) = τ(a(n)); this sequence begins:
1, 2, 3, 2, 3, 2, 5, 4, 3, 2, 9, 4, 3, 4, 7, 2, 5, 6, 5, 2, 9, 4, 3, 4, 15, 2, 3, 2, 9, 4, 9, 4, 9, 2, 3, 8, 15, 4, 3, 4, 15, 2, 9, 8, 9, 2, 3, 4, 21, 4, 9, 4, 7, 6, 11, 6, 25, 6, 5, 6, 13, 2, 15, 4, 3, 4, 27, 8, 3, 2, 9, 8, 9, 2, 9, 4, 3, 2, 9, 10, 9, 4, 21, 2, 3, 8, 27, 4, 3, 8, 15, 4, 15, 4, 9, 2, 3, 2, 27, 4, 15, 4, 9, 8, 15, 2, 3, 4, 21, 8, 9, 2, 21, 2, 9, 4, 9, 4, 3, 8, 45, 2, 3, 10, 9, 4, 15, 2, 9, 4, 27, 4, 3, 4, 15, 8, 9, 2, 27, 4, 3, 4, 35, 6, ...
Records r begin as follows:
1, 3, 6, 8, 12, 16, 18, 28, 30, 44, 58, 70, 78, 86, 96, 116, 130, 148, 160, 182, 204, 220, 260, 312, 340, 380, 406, 474, 514, 538, 552, 556, 616, 656, 686, 786, 842, 878, 900, 918, 958, 982, 1000, 1092, 1190, 1272, 1290, 1378, 1428, 1432, 1540, 1612, 1776, 1880, 1946, 2126, 2226, 2284, 2290, 2452, ...
These appear at the following indices:
1, 2, 3, 5, 13, 16, 21, 23, 26, 28, 33, 35, 37, 39, 41, 54, 59, 61, 66, 79, 81, 86, 103, 129, 138, 164, 175, 177, 179, 181, 183, 214, 219, 230, 258, 260, 262, 264, 266, 280, 282, 284, 286, 327, 364, 366, 384, 386, 388, 423, 459, 498, 513, 534, 576, 578, 580, 582, 644, 646, 659, 673, 686, 711, 756, 781, 783, 785, 818, 820, 822, 824, 826, 866, 868, 870, 872, 921, 923, 925, ...
We see a(n) = 1 for n in the following (see A350615):
1, 8, 12, 20, 742, 513152128
These are the only occasions of m = 1 for a(1..109), the last index shown attributable to Hans Havermann.
The first appearance of 2k appears at the following indices:
1, 7, 6, 5, 16, 737, 736, 735, 734, 733, 732, 731, 513152116, 513152115, 513152114, 513152113, 513152112, 513152111, 513152110, 513152109, 513152108, 513152107, 513152106, 513152105, 513152104, 513152103, 513152102, 513152101, 513152100, 513152099, 513152098, 513152097, 513152096, 513152095, ...
Hence, a(513152095) = 232, the largest power of 2 seen in a(1..109), the large indices attributable to Hans Havermann. Are there any more powers of 2 in a?
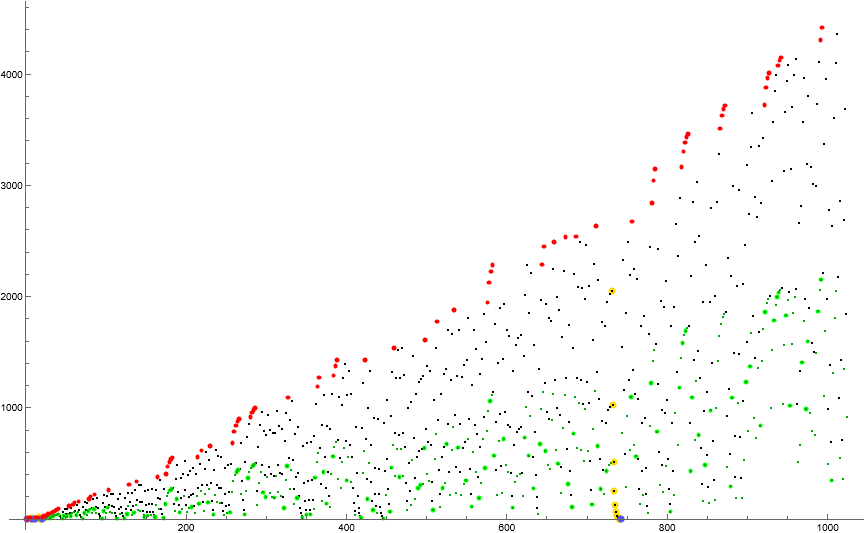
Figure 2: Log-log scatterplot of a(n) for 1 ≤ n ≤ 212 showing maxima r in red, odd terms in green, prime terms with green emphasis, terms 2ε emphasized in gold, and 1’s in blue. The first 48 terms are labeled. Generate using Code 2.
Theorems.
Let us attempt a few theorems regarding this sequence, beginning with several axioms that descend from sequence definition:
Axiom 1: a(1) = k = 1 by definition.
Axiom 2: even input condition: a(n+1) =a(n)/2 iff 2| a(n).
Axiom 3: odd input condition: a(n+1) = a(n) × q, where q = prime(k). Whereupon we have odd input, additionally, we increment k. By this, we know that k is nonincreasing as n increases.
It is presumed the sequence consists of numbers m ∈ ℕ.
Theorem 1. If 2ε is the largest power of 2 that divides even m = a(n), then we have the following:
a(n+j) = m/2(ε−j) : 0 < j ≤ ε.
Proof 1. Direct consequence of Axiom 2. While 2 | m, we set the following term to m/2 until output is no longer even, effectively eliminating 2ε from the prime power decomposition of m after ε iterations. ∎
Corollary 1.1. If 2ε is the largest power of 2 that divides even m = a(n), then a(n+ε) is odd.
Corollary 1.2. If a(n) = 2ε, then a(n+ε) = 1. Hence, for n > 1, a(n) = 1 iff immediately preceded by perfect powers of 2. Given the appearance of a(n) = 2ε, we will have all powers 2(ε−j) : 0 ≤ j ≤ ε in a at a(n+ε−j), respectively.
Corollary 1.3. If m is missing, then 2ε × m is missing for ε ≥ 0.
Proof 1.3. The question of whether m is missing implies that larger terms are also missing. For if m is missing, then 2m is also missing; generally, if m is missing, then 2ε × m is missing via induction and the second axiom.
Suppose m is missing, but we have a(n) = 2ε × m. Then via Theorem 1 we have:
a(n+j) = m/2(ε−j) : 0 < j ≤ ε
until we reach a(n+ε) = m odd, thereby, all the missing terms 2ε × m must appear in the sequence, a contradiction. ∎
Theorem 2. The sequence decreases for m even, and increases for m odd.
Proof 2. As a consequence of Axiom 2, 2 | m ↔ m/2 < m, hence the sequence decreases iff 2 | m. As a consequence of Axiom 3, 2 ⊥ m ↔ m + q : q is prime. If a(n) → a(n+1) ∧ a(n+1) − a(n) = q, then a(n) is odd for n > 2. Given m ∧ q ∈ ℕ, m + q > m, therefore the sequence increases iff 2 ⊥ m. ∎
Corollary 2.1. The fruit of the odd input condition is even for n > 2.
Corollary 2.2. Odd m do not appear adjacently in a outside of a(1..2) = {1, 3}, since 2 is the smallest prime and given incrementation of k after each emergence of odd input. Hence odd m are singletons that represent the bottoming out of a chain of even numbers.
Corollary 2.3. Outside of {1, 3}, if r is a record in a, 2 | r.
Term a(2) = 3 sets a record because a(1) = 1 is odd, therefore a(2) = a(1) + q = 1 + prime(k) = 1 + 2 = 3; 3 > 1, and we increment k such that k = 2. Hence, a(3) = a(2) + q = 3 + prime(k) = 3 + 3 = 6, and we increment k such that k = 3. Therefore, through induction predicated on odd input, the output given an odd input is always even since k is nondecreasing. Since the sequence increases for input m odd and since the fruit of odd input condition is even for n > 2, records r > 3 are even. ∎
Corollary 2.4. Odd a(n) ≤ r/2 and prime a(n) = p ≤ r/2, where r = max(a(1..n)). Therefore, in scatterplot, odd numbers are confined to the lower half of the populated field, and the primes outside of occasions of m = 2, appear among them.
Hans Havermann had examined the terms missing from a given his dataset of 109 terms, beginning with those listed below:
36, 72, 97, 107, 115, 127, 144, 167, 194, 211, 214, 223, 230, 232, 254, 265, 279, 288, 296, 334, 356, 360, 376, 381, 388, 389, 422, 428, 429, 440, 443, 446, 460, 464, 496, 497, 508, 511, 521, 523, 530, 548, 551, 558, 576, 579, 583, 592, 639, 668, 675, 679, 681, 695, 712, ...
The appearance of 36 among these terms, given Corollary 1.3, raises the question why A5010 = { 2ε × 3² } does not appear in a. Similarly, we do not see 10 × A5010. If we could prove that 36 does not appear, we show that a does not cover the natural numbers.
Russ Cox showed a(77534485875) = 144, a(77534485876) = 72, and a(77534485877) = 36.
The original name of this document was “The Hailstone Sequence”. Through correspondence with Neil Sloane, I learned that such is a common name for the 3x+1 or Collatz sequence. Therefore, he suggested “Sisyphus sequence”. Zeus condemned King Sisyphus, who had cheated death, to push a great rock up a mountain, only to have it slip and roll all the way down. Sisyphus was forced to repeat the feat endlessly forevermore. Thanks to Dr. Sloane for the suggestion!
This concludes our examination.
Appendix.
Code 1: Efficiently generate a and store it in the variable a350877.
a350877 = Block[{j = 1, k, q = 2},
{j}~Join~Reap[Monitor[
Do[If[EvenQ[j], k = j/2, k = j + q; Set[q, NextPrime[q]]];
Sow[k]; j = k, {i, 2^20}], i]][[-1, -1]]];]
Block[{nn = 2^12, kk = 48, out = -120, a, r, s, t, u, p},
a = a350877[[1 ;; nn]];
r = Table[If[MemberQ[#, i], a[[i]]], {i, nn}] &@
Map[FirstPosition[a, #][[1]] &, Union@ FoldList[Max, a]];
s = Array[If[# == 1, #] &@ a[[#]] &, nn];
t = Array[If[IntegerQ@ Log2@ #, #, out] &@ a[[#]] &, nn];
u = Array[If[OddQ[#], #] &@ a[[#]] &, nn];
p = Array[If[PrimeQ[#], #] &@ a[[#]] &, nn];
ListPlot[{a, t, a[[1 ;; kk]], a, p, u, s, r,
Array[Labeled[#, #, Top, LabelStyle -> Bold] &@ a[[#]] &, kk]},
ImageSize -> 864, ScalingFunctions -> {"Log2", "Log2"},
Joined -> {False, False, True, False, False, False, False, False},
PlotStyle -> {
Directive[Black, PointSize[Tiny]],
Directive[Hue[1/7], PointSize[Large]],
Directive[Gray, Thin],
Directive[Black, PointSize[Small]],
Directive[Green, PointSize[Medium]],
Directive[Darker@ Green, PointSize[Small]],
Directive[Lighter@ Blue, PointSize[Large]],
Directive[Red, PointSize[Medium]],
Transparent
}]]
Concerns sequences:
A000040: Primes.
A000079: 2n.
A005010:
2n × 3².
A007814: 2-adic valuation of n.
A350615: Positions of 1s in a.
A350616: Indices of odd terms in a.
A350617: Odd terms in a.
A350618: Successors of odd terms in a.
A350619: Records r.
A350877: Sequence a.
Document Revision Record.
2022 0122 1300 Draft.
2022 0122 1430 Final.
2022 0123 1000 Corollary 1.3, missing terms, Havermann’s additional 1, N. J. A. Sloane’s auxiliary sequences.
2022 0123 1530 Revision of name.