The Catch-Up Sequence.
A sequence by Scott Shannon, this page written by Michael Thomas De Vlieger, St. Louis, Missouri, 2022 0426.
Abstract.
Scott Shannon’s A352867 is a lexically earliest sequence (LES) tantamount to the recursive mapping of f(i, j) → k (See Function 1). The scatterplot of the sequence exhibits a curious series of runs, conspicuously, those of even numbers, but more generally, those having a common factor g. We examine this sequence to attempt to understand the scatterplot and runs of common factor g.
Introduction.
Scott Shannon posed a sequence akin to the Yellowstone sequence (A098550) and similar sequences. This sequence is A352867, defined by Shannon as A(1) = 1, A(2) = 2; for n > 2, A(n) is the smallest positive number that has not appeared that shares a factor with A(n−1), A(n−2), and A(n−1) + A(n−2). Let i = A(n−2), j = A(n−1), and and S = (i + j).
We employ a dimensioned variable c(k) = n to store the index of k in A. This alleviates searching a list of many terms to determine k ∈ A.
In Shannon’s definition, it is not clear how A(3) = 6 might appear since A(1) = i = 1 and coprime to all numbers; it seems that he employed the notion that 1 is a factor of 6. If we presume that 6 is given, then we can use a simpler definition that employs non-coprimality (that is, output y belongs to the cototient of an input x). Conceived this way, the sequence is tantamount to the recursive mappings of the following function f(x):
{f(i, j) → k : (i, k) > 1 ∧ (j, k) > 1 ∧ (S, k) > 1 ∧ k ∉ A(1..n−1) ∧
((i, K) > 1 ∧ (j, K) > 1 ∧ (S, K) > 1 ∧ K ∉ A(1..n−1) ∧ k < K},
using the seed terms A(n) = n : n ≤ 2, and A(3) = 6.
The first terms of a follow:
1, 2, 6, 4, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, 102, 104, 106, 108, 110, 112, 105, 7, 21, 35, 49, 63, 77, 91, 119, 126, 133, 140, 114, 116, 118, 120, 122, 124, 128, 130, 132, 134, 136, 138, 142, 144, 146, 148, 150, 152, 154, 156, 158, 160, 162, 164, 166, 168, 170, 172, 174, 176, 165, 11, 33, 55, 99, 121, 143, 187, 198, 209, 220, 228, 178, 180, 182, 184, 186, 188, 190, 192, 194, ...
We have the following axioms:
Lexical Axiom: k ∉ A(1..n−1) ∴ i ≠ j ≠ k.
Earliest Axiom:
If M > m and M also satisfies the other axioms, A(n) = m.
Non-Coprimality Axiom: (i, k) > 1 ∧ (j, k) > 1 ∧ (S, k) > 1.
These axioms have the effect of highlighting parity and primality. Primes appear late, while even numbers tend to enter early.
Auxiliary sequences.
The sequence S(n) = A(n−2) + A(n−1) begins:
0, 1, 3, 8, 10, 12, 18, 22, 26, 30, 34, 38, 42, 46, 50, 54, 58, 62, 66, 70, 74, 78, 82, 86, 90, 94, 98, 102, 106, 110, 114, 118, 122, 126, 130, 134, 138, 142, 146, 150, 154, 158, 162, 166, 170, 174, 178, 182, 186, 190, 194, 198, 202, 206, 210, 214, 218, 222, 217, 112, 28, 56, 84, 112, 140, 168, 210, 245, 259, 273, 254, 230, 234, 238, 242, 246, 252, 258, 262, 266, 270, 274, 280, 286, 290, 294, 298, 302, 306, 310, 314, ...
Records r begin as follows:
1, 2, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, 102, 104, 106, 108, 110, 112, 119, 126, 133, 140, 142, 144, 146, 148, 150, 152, 154, 156, 158, 160, 162, 164, 166, 168, 170, 172, 174, 176, 187, 198, 209, 220, 228, 230, 232, 234, 236, 238, 240, 242, 244, 246, 248, 250, ...
Table 1 lists n, A(n) = U, where U is a local minimum of A if A is a permutation of natural numbers:
n U = A(n)
------------
1 1
2 2
3 166
5 239
13 333
17 670
23 1841
31 2274
59 12552
61 13325
83 50529
107 57313
113 69893
127 114406
137 205920
139 243134
157 248705
...
Let g = ⊠(i, j, i+j) = A7947(gcd(i, j, i+j)). Then the sequence G(n) begins as follows, writing 0 when we do not have 2 previous terms:
0, 0, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 2, 2, 2, 2, 2, 2, 2, 2, 2, ...
Code 2 provides Mathematica script that generate these auxiliary sequences.
Theorems.
Theorem 1. Lexically earliest sequences imply division of the range of f(i, j) into 3 zones:
1. Saturation: k < u → k ∈ A(1..n), i.e., prohibition by Axiom 1.
2. Open: k > r → k ∉ A(1..n), i.e., satisfaction of Axiom 1.
3. Semi-saturation: u ≤ k ≤ r; c(k) < n → k ∈ A(1..n), prohibition by Axiom 1.
else, satisfaction of Axiom 1.
These are consequences of Axioms 1 and 2. Further consequences include the following:
1. There is a smallest missing number u in A(1..n−1).
2. There is a largest number r in A(1..n−1).
3.
Let register c(k) = n be the index of k in A. In algorithm, we initialize c(k) = 0 and for A(n) = k, we set c(k) = n. (We may simply use c(k) as a flag, 1 iff k ∉ A(1..n-1) else 0). If A is a permutation of ℕ, then c is the inverse permutation of A.
We note that u is odd for n > 1. This implies a smallest missing even number v > u.
Theorem 2. Prime p = k is forced into divisorship of both input and output.
Proof 2. Prime p | m ⋁ p ⊥ m, ∴ p | i ∧ p | j ∧ p | S → p, given axiomatic prohibition of coprimality and through axiomatic inequality we have i ≠ j ≠ k. Similarly, p | k when p is any of i, j, or i+j.∎
Corollary 2.1. (i, j, i+j) = p ∧ p ∉ A(1…n−1) → k = p. This means that the appearance of odd prime p in this sequence requires that 2 most recent terms are divisible by p, as well as their sum S.
Corollary 2.2. Aside from the trivial local minimum 1, the local minima are prime. If A is not a permutation of natural numbers, we mean to say that primes appear late in A.
We observe that many consecutive even terms arise in A, and then we see consecutive odd multiples mq : q is prime.
Theorem 3. 2 | i ∧ 2 | j ∧ 2 | S → 2 | k iff ¬∃ odd prime q ∉ A(1…n−1) ∧ q | i ∧ q | j ∧ q | S.
Proof 3. 2 | S iff i and j have same parity, otherwise S is odd. We generalize to say that prime p | S iff either (p | i ∧ p | j) ∨ (i ≡ +m mod p ∧ j ≡ −m mod p). ∎
Observation: Even k appear early in A, i.e., 2 | A(n) ≥ n. This stands to reason since 2 is the smallest prime with the least displacement in the cototient of even numbers. The fixed points in A(1..2¹⁸) are {1, 2, 4, 63}; 2 and 4 are the only even A(n) : A(n) = n. Note that many odd k appear early as well.
Corollary 3.1. Odd prime q ∉ A(1…n−1) ∧ q | i ∧ q | j ∧ q | S ∧ p ∉ A(1…n−1) ∧ p | i ∧ p | j ∧ p | S ∧ q ≠ p ⇒ q | k.
For prime q > 2, to enter the sequence, q must divide both A(n−2) and A(n−1), as well as their sum S.
Corollary 3.2. qε enters the sequence iff g = p.
Proof:
Let p be the smallest prime divisor of k and let q > p. It is clear that k may enter the sequence iff g | k and k also satisfies the lexically earliest axioms. If g = p, and k is the lexically earliest solution for n, then it enters the sequence earlier than it might if g = q. Through Corollary 2.1, primes enter the sequence iff p | i ∧ p | j ∧ p | S. Since the Non-Coprimality Axiom requires at least 1 distinct prime divisor in common with each of i, j, and i+j, a number k = qε: ω(k) = 1 requires g = q. ∎
This corollary implies that we may use a computation approach similar to the Rains algorithm for A064413 to efficiently generate A.
Partition of A into intervals based on the squarefree kernel of (i, j, i+j).
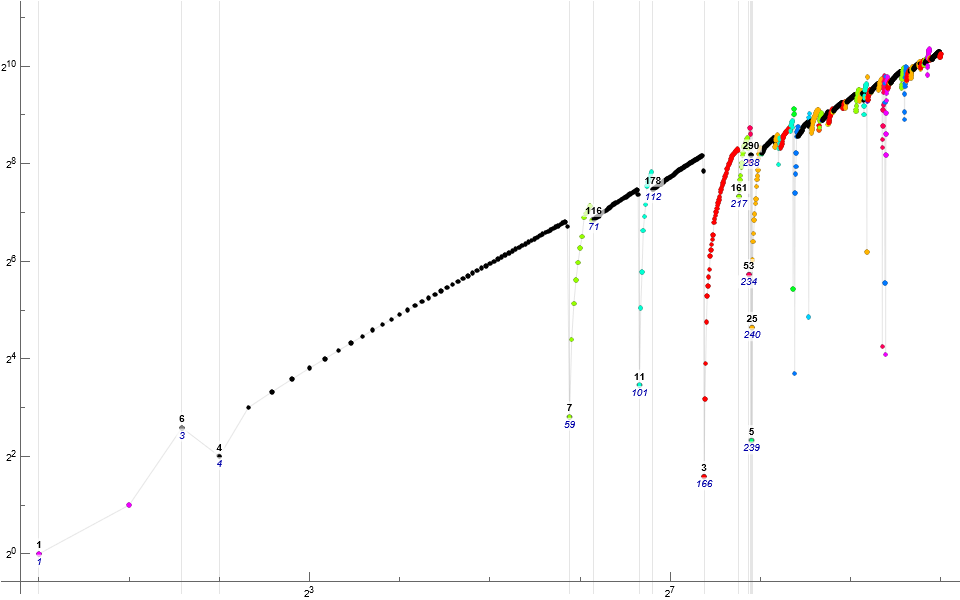
We can use G to partition A into intervals of same value. (See Figure 2.) Example: G(4..59) = g = 2. We see that A(4..58) contains a run of 53 even numbers and A(58) = 105, which ends the run and introduces A(59) = 7.
Ignoring the given terms {1, 2, (6)}, we thus have:
4, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40,
42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74,
76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, 102, 104,
106, 108, 110, 112;
105, 7, 21, 35, 49, 63, 77, 91, 119, 126, 133, 140;
114, 116, 118, 120, 122, 124, 128, 130, 132, 134, 136, 138, 142, 144,
146, 148, 150, 152, 154, 156, 158, 160, 162, 164, 166, 168, 170,
172, 174, 176;
165, 11, 33, 55, 99, 121, 143, 187, 198, 209, 220;
228, 178, 180, 182, 184, 186, 188, 190, 192, 194, 196, 200, 202, 204,
206, 208, 210, 212, 214, 216, 218, 222, 224, 226, 230, 232, 234,
236, 238, 240, 242, 244, 246, 248, 250, 252, 254, 256, 258, 260,
262, 264, 266, 268, 270, 272, 274, 276, 278, 280, 282, 284, 286, 288;
231, 3, 9, 15, 27, 39, 45, 51, 57, 69, 75, 81, 87, 93, 111, 117, 123,
129, 135, 141, 147, 153, 159, 171, 177, 183, 189, 195, 201, 207,
213, 219, 225, 237, 243, 249, 255, 261, 267, 273, 279, 285, 291,
294, 297, 300, 303, 306, 309, 312, 315;
308, 161, 175, 203, 217, 245, 259, 287, 301, 322, 329, 336, 343, 350,
357, 364, 371;
318, 53, 265, 424;
390;
290;
5, 25, 65, 85, 95, 115, 125, 145, 155, 185, 205, 215, 235, 275, 295, 305, 310;
320;
292, 296, 298, 302, 304, 314, 316, 324, 326, 328, 330, 332, 334, 338,
340, 342, 344, 346, 348, 352, 354, 356, 358, 360, 362, 366, 368, 370;
...
A(58) = 105 is the first odd term since A(1) = 1. We see i = 110 and j = 112, their sum S = 222. Surely, 2 divides all of these and v = 114 as well, however, 5 divides i and 105, 7 divides j and 105, and 3 divides S and 105; 105 < v. Therefore, A(58) = 105.
A(59) = 7, since i = 112, j = 105, and since 7 | i ∧ 7 | j, 7 | S = 217. It is clear, thus, that a run of multiples of 7 will appear, indeed, 7 divides A(53..69), numbers that for the largest n in that range have mixed parity. At a certain point, m : 7 | m prove larger than some k that is not coprime to all of i, j, and S. This point is reached at A(70) = 114 = 2 × 3 × 19, as 19 | 133, 2 | 140, and 3 | 273.
Table A lists the first 3 dozen intervals and the common value g = G(n..n+d−1), where d is the length of the run of g. It demonstrates that the sequence does not toggle based on parity but instead by g.
Hence it is plain to see A is prone to runs of even k until odd prime q divides all of A(n−2), A(n−1), and A(n−2) + A(n−1). Since a run of even k consumes all even possibilities to a point, odd terms become readily available. If q divides all of A(n−2), A(n−1), and A(n−2) + A(n−1), and q | k, then in the next iteration, the same situation subtends until all odd possibilities q | k ∉ A(1…n−1) enter A. This subtends until we reach the point where the run of evens was suspended. This is because odd q | i ∧ q | j have consumed missing odd terms, hence i and j have same parity and S is even. When all missing odd q | k are consumed, we begin to admit even k divisible by q. Once 2 | i ∧ 2 | j, S is also even and we recommence consuming even numbers.
Table 2 below shows the frequency of (squarefree) 1 ≤ g ≤ 19 in A(1..2¹⁸).
g card. n
------------------
1 1 3
2 117208 4
3 53788 166
5 23957 240
6 1695 431
7 17008 59
10 648 239
11 8593 101
13 6331 333
14 287 411
15 158 1062
17 3993 670
19 4069 653
...
Generally smaller prime g are more frequent than larger primes, and smaller composite g more frequent than larger composites.
Conjecture 4. A is a permutation of the natural numbers.
Proof Sketch 4. We use a similar approach to Corollary 3.2. Let p be the smallest prime divisor of k and let q > p. It is clear that k may enter the sequence iff g | k and k also satisfies the lexically earliest axioms. Theorem 2 describes the process of prime p entering A through divisorship of each of i, j, and i+j, and through the generalization of Theorem 3, we see that p | (i+j) iff p | i ∧ p | j ∨ (i ≡ +m mod p ∧ j ≡ −m mod p). Therefore, the sequence admits p and multiples mp = k until there exists a smaller solution to the axioms which changes g. We return to those multiples mp whereupon g = p to consume the smallest unused numbers p | u until there exists a smaller solution to the axioms which changes g. With this and the fact that g = 2 dominates, that even A(n) ≥ n (i.e., {2, 4} are fixed points; generally even A(n) > n), we assert that A is a permutation of natural numbers.
Constitutive analysis of A.
We examine the constitutive binary relations of {i, k}, {j, k}, and {i+j, k} so as to see patterns in the sequence A. The constitutive binary relations are explained by [1]. We concatenate the states of these three relations to obtain a constitutive code for each term, appending 000 for the first two terms since these are given. The constitutive states are recapitulated in Table B.
The Lexical Axiom prohibits state ⑤ since x | y ∧ y | x ⇒ x = y. The Non-Coprimality Axiom probibits state ⓪, except among terms A(1..3) = {1, 2, 6}, where 1 is coprime to 2 and 6, 2 is coprime to 1 and 6 is coprime to 1 (see the definition of state 0 in [1]).
As seen in [1], primes p require input in state ② and output in state ④, while prime powers pε requires input in ③ and output in ⑦. In this sequence, through Corollary 2.1, we have state ② pertaining to i, j, i+j vis-a-vis k = p prime. Therefore, we see ℭ(i, j, i+j) = “222” for A(n) = p prime. Thereafter, we have “_4_” followed by “4__”, except in the case of p = 3, where the following term 9 has “362”, and p = 5, where the following term 25 has “363”. (State ⑥ arises for p | p².) The predominant mode of A is in state ℭ = “111” as expected. There are only a few instances of exotic states ⑧ and ⑨, these seem to be limited to between k and S. The most common exotic state is “118”.
The most exotic state is ⑨, which requires numbers x and y nondivisors of one another, each having the same set of more than 1 distinct prime divisor. The simplest manifestation of the state concerns x = 12 and y = 18. We have precisely 2 appearances of state ⑨ in A(1..2¹⁸). We see that A(7) = 12 is a nondivisor regular of A(5) + A(6) = 8 + 10 = 18. Also, A(928) = 1156 is a nondivisor regular of A(926) + A(927) = 1037 + 1139 = 2176; the distinct prime factors of 1156 and 2176 are 2 and 17. Due to the nature of the mutually nondivisor-regular binary relation, it is increasingly unlikely that we may have another instance of state ⑨ in the sequence as n increases.
Table C summarizes the constitutive states seen in A(1..2¹⁸).
Conclusion.
Shannon’s A352867 is a lexically earliest sequence (LES) beginning with {1, 2, 6} that is the recursive mapping of f(i, j) → k (See Function 1). The scatterplot of the sequence exhibits a curious series of runs, conspicuously, those of even numbers, but more generally, those having a common factor g. The sequence shares the qualities of all LES, including the Lexical and Earliest (greedy) Axioms and Theorem 1. Function 1 bans comprimality among output k and each of the 2 most recent terms i = A(n−2) and j = A(n−1) as well as their sum, S = i+j, embodied by the Non-Coprimality Axiom. Hence, through the LES axioms and Theorem 2, primes are forced into divisorship of all of i, j, and i+j, consequently appearing late in the sequence. We may define a sequence G = {A7947(gcd(i, j, i+j)) ↦ A} where g = G(n), and writing G(1..2) = {0, 0} since A(1..2) are given. We then can partition A according to runs of the same value g and thereby neatly compartmentalize the behavior of the sequence as shown by Figure 2. Looking at A using binary relations based on the prime decomposition of i, j, i+j, and k, we can visualize some of the theorems manifested in the sequence.
Conjecture 4 gives a proof sketch regarding A352867 as a permutation of natural numbers.
This concludes our examination..
Appendix.
Table A: Sequence G partitioned into intervals G(n..n+d−1) = g. We use offset 0 since the zeros in G are merely placeholders regarding A(1..2) that are given terms. Example: G(4..58) = g = 2.
i G(n) d n
------------------
0 0 2 1
1 1 1 3
2 2 55 4
3 7 12 59
4 2 30 71
5 11 11 101
6 2 54 112
7 3 51 166
8 7 17 217
9 53 4 234
10 2 1 238
11 10 1 239
12 5 17 240
13 10 1 257
14 2 28 258
15 5 8 286
16 11 5 294
17 3 24 299
18 11 6 323
19 43 4 329
20 13 9 333
21 2 29 342
22 29 4 371
23 2 4 375
24 5 22 379
25 3 1 401
26 21 1 402
27 7 8 403
28 14 1 411
29 2 19 412
30 6 1 431
31 3 15 432
32 6 1 447
33 2 34 448
34 3 10 482
35 5 5 492
36 2 36 497
...
Table B summarizes the constitutive binary relations and their qualities. Examples appear in the note. For coprimality, we may consider any 2 dissimilar primes p and q. Symmetrical divisibility applies only to k = n. (Here we use ℭ to denote the constitutive state.)
| ℭ | | | binary relation | abb. | sym. | neut. | reg. | rev. | note |
| ---- | | | ------------------ | ------ | ------ | ------ | ------ | ------ | ---------------- |
| ⓪ | | | k ⊥ n ∧ n ⊥ k | ⊥ | ✓ | ⓪ | ∀ p, q, p ≠ q | ||
| ① | | | k ◊ n ∧ n ◊ k | ◊.◊ | ✓ | ✓ | ① | 6, 10 | |
| ② | | | k ◊ n ∧ n | k | ◊.| | ④ | 30, 6 | |||
| ③ | | | k ◊ n ∧ n || k | ◊.|| | ✓ | ⑦ | 30, 12 | ||
| ④ | | | k | n ∧ n ◊ k | |.◊ | ② | 10, 30 | |||
| ⑤ | | | k | n ∧ n | k | |.| | ✓ | ✓ | ⑤ | ∴k = n | |
| ⑥ | | | k | n ∧ n || k | |.|| | ✓ | ⑧ | 6, 12 | ||
| ⑦ | | | k || n ∧ n ◊| k | ||.◊ | ✓ | ③ | 20, 30 | ||
| ⑧ | | | k || n ∧ n | k | ||.| | ✓ | ⑥ | 20, 10 | ||
| ⑨ | | | k || n ∧ n || k | ||.|| | ✓ | ✓ | ✓ | ⑨ | 12, 18 |
Table C: Summary of constitutive states seen in A(1..2¹⁸). We concatenate ℭ(i, k), ℭ(j, k), and ℭ(i+j, k), where ℭ(x, y) is the constitutive binary relation of x and y.
ℭ card. n A(n-2)=i A(n-1)=j S=i+j A(n)=k
--------------------------------------------------------
000 2 1 0 0 0 0
044 1 3 1 2 3 6
111 260860 8 10 12 22 14
112 329 287 345 325 670 335
113 166 13 20 22 42 24
117 32 16 26 28 54 30
118 195 1608 1940 1928 3868 1934
119 1 928 1037 1139 2176 1156
131 14 256 305 310 615 320
141 35 235 318 53 371 265
142 1 227349 254419 229 254648 31831
171 97 18 30 32 62 34
173 2 10 14 16 30 18
177 1 1202 1219 1325 2544 1590
211 1 20432 23542 23463 47005 11771
222 53 59 112 105 217 7
241 2 60 105 7 112 21
311 51 83 138 142 280 144
333 81 9 12 14 26 16
362 2 167 231 3 234 9
363 14 5 6 4 10 8
411 26 61 7 21 28 35
413 1 236 53 265 318 424
415 4 331 43 516 559 559
471 16 168 3 9 12 15
611 1 104 33 55 88 99
633 7 169 9 15 24 27
638 1 4 2 6 8 4
711 142 11 16 18 34 20
713 1 19 32 34 66 36
719 1 7 8 10 18 12
771 1 6 4 8 12 10
Figure 1: Annotated log-log scatterplot of A(n) for 1 ≤ n ≤ 210. Figures in red are records, blue local minima, gold fixed points. Primes are accentuated in green.
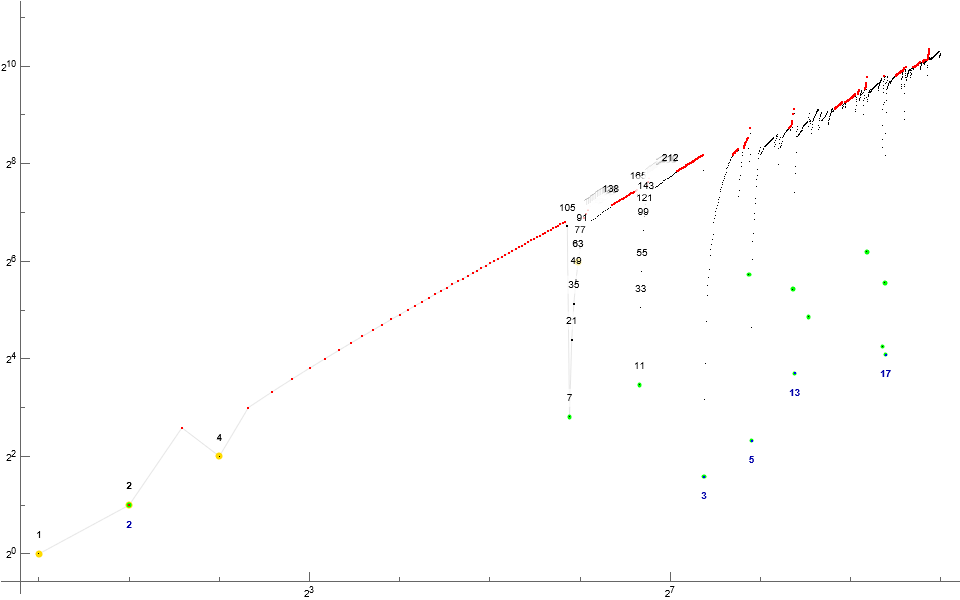
Figure 2: Annotated log-log scatterplot of A(n) for 1 ≤ n ≤ 210, partitioned into intervals according to the value of G. We label G in black and n in blue for the first term in these intervals. Gridlines are made to indicate intervals for n ≤ 2⁸. (See Code 3).
References:
[1] Michael De Vlieger, Constitutive Relations, Sequence Analysis, 2021.
Code 1: Generate a and store it in the variable a352867:
a352867 = Block[{nn = 2^16, a, c, k, s, u = 1}, c[_] = 0; s = {1, 2, 6};
MapIndexed[Set[{a[First[#2]], c[#1]}, {#1, First[#2]}] &, s];
While[c[u] > 0, u++];
Monitor[Do[k = u;
While[Nand[c[k] == 0, ! CoprimeQ[#1, k], ! CoprimeQ[#2, k], ! CoprimeQ[#3, k]], k++] & @@
{#1, #2, #1 + #2} & @@ {a[i - 2], a[i - 1]};
Set[{a[i], c[k]}, {k, i}];
If[a[i] == u, While[c[u] > 0, u++]], {i, Length[s] + 1, nn}], i];
Array[a, nn]]
Code 2: Generate auxiliary sequences.
a352867u = Block[{u = 1, c, s = a352867}, c[_] = 0;
Reap[Do[Set[c[s[[i]]], i]; If[s[[i]] == u, While[c[u] > 0, u++]];
Sow[u], {i, Length@s}]][[-1, -1]]];
a352867uu = Union@a352867u (* local minima *);
a352867ui = Block[{u = 1, c, s = a352867}, c[_] = 0;
Reap[Do[Set[c[s[[i]]], i];
If[s[[i]] == u, While[c[u] > 0, u++]; Sow[i]], {i, Length@ s}]][[-1, -1]]];
Set[{a352867r, a352867ri}, Block[{r = 1, c, s = a352867},
Transpose@ Reap[Do[Set[c[s[[i]]], i];
If[# > r, r = #; Sow[{r, i}]] &@s[[i]], {i, Length@ s}]][[-1, -1]]]]
(* records transform *);
a352867ril = Part[SplitBy[Differences@ a352867ri, 1] /.
w_List /; First[w] == 1 :> {Length[w]}, All, 1];
(* Run lengths of first differences of indices of records. *);
a352867f = Block[{s = a352867},
Reap[Do[If[i == s[[i]], Sow[i]], {i, Length@ s}]][[-1, -1]]]
(* Fixed Points *);
a352867p = Select[a352867, PrimeQ];
a352867pi = Map[FirstPosition[a352867, #][[1]] &, a352867p];
a352867s = Total /@ Partition[a352867, 2, 1] (* Sum S = i + j *);
a352867gg = Block[{s = a352867}, {0, 0}~Join~
Reap[Do[Sow@GCD[#1, #2, #3] & @@ {#1, #2, #1 + #2} & @@
s[[i - 2 ;; i - 1]], {i, 3, Length[s]}]][[-1, -1]]];
a352867g = Map[Times @@ FactorInteger[#][[All, 1]] &, a352867gg];
Code 3: Generate Figure 2.
Block[{nn = 2^10, kk = 2^8, a, g},
a = a352867[[1 ;; nn]]; g = a352867g[[1 ;; nn]];
ListPlot[{
a[[1 ;; nn]], Which[# == 1, Gray, # == 2, Black, True, Hue[(# - 3)/17]] &@
g[[#]]] &, nn],
Array[If[MemberQ[a352867gi, #],
Labeled[#, #, Top, LabelStyle -> Directive[Bold, Black]] &@
a[[#]]] &, kk],
Array[If[MemberQ[a352867gi, #],
Labeled[a[[#]], #, Bottom, LabelStyle -> Directive[Italic, Darker@ Blue]]] &, kk]},
ImageSize -> 960,
Joined -> {True}~Join~ConstantArray[False, 4],
ScalingFunctions -> {"Log2", "Log2"},
GridLinesStyle -> Lighter@ LightGray,
GridLines -> {TakeWhile[a352867gi, # <= kk &], None},
PlotStyle -> {
Directive[Gray, Thin],
Directive[Black, PointSize[Medium]] }] ]
Concerns sequences:
A007947: Squarefree kernel of n.
A352867: Sequence A.
Document Revision Record.
2022 0407 2200 Draft.
2022 0427 2200 Second draft.
2022 0428 1530 Final.