OEIS A353125.
A sequence by David Sycamore, this page written by Michael Thomas De Vlieger, St. Louis, Missouri, 2022 0508.
Abstract.
We example an inventory sequence A = A353125 with payload function A1414(k) = ξ(k). This sequence features a finite cardinality of m in multiset A. This cardinality c(m) ≤ A607(m) + τ(m) − 2. We show that 10 composite m behave as primes do in that c(m) = A607(m). These composite m ∈ {6, 9, 15, 25, 35, 49, 77, 121, 143, 169}.
Introduction.
David Sycamore defined OEIS A353125 as a multiset known as an “inventory sequence” beginning with 2 and if the previous term j is a novel term (appearing in A(1..n−1) exactly once), then A(n) = the sum of prime factors of j with repetition, else A(n) = j × c( j), where c( j) is the number of copies of j in A(1..n−1).
Let A(1) = 2 and let c( j) signify the number of copies of j in A(1..n−1). We employ the symbol “∈” to signify that j appears in multiset A(1..n−1) at least once. Let j = A(n−1). Then if c( j) = 1, A(n) = ξ( j) = A1414( j), otherwise A(n) = j × c( j).
Consider A607(n) = | λp(n) |, the number of prime partitions of n. Ex.: A607(12) = 2 + 2 + 3 = 7 since 12 = 2² × 3 = 2 × 2 × 3.
Consider OEIS A1414( j) = ξ( j) = ∑{i = Ω( j)} A027746( j, i) ∴ j ∈ ℕ ∧ j ≥ 2. (ξ after Kevin Brown).
Theorem: ξ covers ℕ \ {1}.
Proof: ξ > 1 since 2 is the smallest prime. ξ(p) = p, thus we cover ℙ. Generally ξ(k) = ∑{p | k} p, therefore we are concerned with whether A607(n) > 0 : n > 1. (Sycamore:) Let k = p₁ + p₂ + … + pi be any prime partition of k (there are A607(k) of them to choose from, so we can take our pick). Then let h = p₁ × p₂ × … × pi. So then we have ξ(h) = k. Thus ξ covers ℕ \ {1}.∎
The first terms of A follow:
2, 2, 4, 4, 8, 6, 5, 5, 10, 7, 7, 14, 9, 6, 12, 7, 21, 10, 20, 9, 18, 8, 16, 8, 24, 9, 27, 9, 36, 10, 30, 10, 40, 11, 11, 22, 13, 13, 26, 15, 8, 32, 10, 50, 12, 24, 48, 11, 33, 14, 28, 11, 44, 15, 30, 60, 12, 36, 72, 12, 48, 96, 13, 39, 16, 32, 64, 12, 60, 120, 14, 42, 12, 72, 144, 14, 56, 13, 52, 17, 17, 34, 19, 19, 38, 21, 42, 84, 14, 70, 14, 84, 168, 16, 48, 144, 288, 16, 64, 128, 14, 98, 16, 80, 13, 65, 18, 36, 108, 13, 78, 18, 54, 11, 55, 16, 96, 192, 15, 45, ...
We have the following axioms:
Axiom 1 (novel condition): If c( j) = 1 then k = ξ( j).
Axiom 2 (extant condition): If c( j) > 1 then k = j × c( j).
Theorems.
Theorem 1: Axiom 1 ⇒ j ≥ 2 ⇒ k ≥ 2. The axiom implies j ≥ 2 which in turn implies k ≥ 2.
Proof: j = 1 is the empty product, hence the sum of its prime factors is 0. If j > 1, then j is the product of at least 1 prime, and the smallest of primes is 2, therefore j ≥ 2. ∎
Theorem 2: Axiom 2 ⇒ j ≥ 2 ⇒ k ≥ 4. The axiom implies j ≥ 2 which in turn implies k ≥ 4.
Proof: Since j ≥ 2 and c( j) ≥ 2 by definition of axiom, k ≥ 4. ∎
Corollary 2.1: k = 2 iff c( j) = 1.
Corollary 2.2: 3 ∉ A, since 3 → 3 through Axiom 1, but there is no way to introduce 3 through Axiom 2.
Let q₁(k) be the total number of copies of k in A via Axiom 1, q₂(k) same through Axiom 2, and Q(k) the total number of copies of k in A, whereas c(k) is the total number of copies of k in A(1..n−1).
Theorem 3: Axiom 1 → k : q₁(k) = A607(k). Axiom 1 furnishes precisely A607(k) copies of k in A.
Proof: Axiom 1 pertains to novel j, that is, j : c( j) = 1, which can happen precisely once per j. The axiom applies ξ( j) → k. We know that function ξ has range [2…∞. Therefore we cover the range of A ∋ { ℕ \ {1, 3} } through ξ. Furthermore, all products in row k of A064364 appear once in A as a result of Axiom 1. Therefore, Axiom 1 delivers A607(k) copies of k in A. ∎
Corollary 3.1: For prime p, q₁(p) = A607(p).
Proof: Axiom 2 requires c( j) > 1 and j = 1 ∉ A; we note that p × c(p) is the product of 2 integers greater than 1, thus necessarily composite. Hence Axiom 1 yields copies of p alone; Axiom 2 does not contribute copies of p into A.∎
Corollary 3.2: For prime p, p → p once. All primes thus appear duplexed, that is, in a run of length ℓ = 2. Furthermore, if A(n) = p ∧ c(p) = 1, i.e., A(n) is the first appearance of p in A, then A(n+1) = p. Consequence of Axiom 1.
Corollary 3.3: k ← j = ∏ ↦ λp(k) ∧ c( j) = 1. k follows novel j iff j is the product of a prime partition of k.
Consider irregular triangle A64364 =
T(k, A607(k)) ∋ ∪{ m : ξ(m) = k }, where row k is the list of prime partitions of k. Ex.: T(12) ∈ {35, 42, 50, 60, 64, 72, 81}, since
λp(12) ∈ {{7,5}, {7,3,2}, {5,5,2}, {5,3,2,2}, {3,3,3,3}, {3,3,2,2,2}, {2,2,2,2,2,2}},
∴ ∏ ↦ λp(12) = {35, 42, 50, 60, 64, 72, 81}.
It follows that such j, appearing for the first time, yields k this way:
Since j = p₁ × p₂ × … pi,
then k = p₁ + p₂ + … pi,
and all the prime factors of j are prime partitions of k, hence k = ξ( j) which is the definition of Axiom 1 that pertains to novel j.
Theorem 4: Axiom 2 → k : q₂(k) ≤ A70824(k).
Proof: Axiom 2 pertains to extant j, that is, j : c( j) > 1. The axiom applies j × c( j) → k, where c( j) strictly increments on each occasion of j in A. Thus, we may write k = c( j) = d × d' : d | k ∧ d > 1 ∧ d' < (k−1), and either we have d copies of d' to furnish k, or d' copies of d to furnish k. Since 1 is not in the sequence and Axiom 2 requires more than 1 copy of j, the trivial complementary divisor pair d × d' = 1 × k is not available. We know the factorization of k is unique, therefore, we might produce all τ( j)−2 combinations of j × c( j) = d × d' = k iff j appears infinitely in A. The cardinality of primes is A607(p), i.e., finite, through Corollary 3.1 and products p × c(p) are in fact limited in number. Indeed, we have at most τ( j)−2 copies of composite j through Axiom 2 and at most A607(j) copies of any j > 1 through Axiom 1 which sum to a finite number. ∎
This theorem fortifies Corollary 3.1. In fact, Q(p) = A607(p), because the trivial divisor pair 1 × p is not available, and these are the sole divisors of prime p.
Corollary 4.1: Q(k) ≤ A607(k) + τ( j) − 2.
Corollary 4.2: j × c( j) → k favors large j and small c( j) : j | k. j₂ = A32742(k) = the largest proper divisor d | k iff q₂(k) = 1.
Corollary 4.3: Axiom 2 furnishes k with j that are smaller than any j that produces k through Axiom 1.
Let j₂ → k via Axiom 2. Thus, j₂ | k ⇒ j₂ < k, since Axiom 2 requires c( j) > 1. As regards Axiom 1, the smallest j₁ → k is A56240(k). A56240(k) ≥ k with equality iff prime k and k = 4. For prime k and k = 4, we see that j₂ < j₁ (if j₂ could yield prime k), therefore in all cases, j₂ < j₁.
Corollary 4.4: If k appears as the consequence of Axiom 1, then the next occurrence (if it occurs) must also be consequent to Axiom 1, it cannot be as a consequence of Axiom 2.
Proof: If k is prime then all occurrences result from Axiom 1 (the primeness of m prevents any other possibility, cf. Corollary 3.1). Suppose that k is composite. Then its first occurrence must be as consequence of novel term j such that ξ( j) = k. Assume that the next occurrence of k is as consequence of a term j seen multiple times already (Axiom 2), thus at its second appearance we have k = w × t, where t > 1 has occurred before, and now appears for the w-th time, where w ≥ 2. (this is permissible because k is composite). Now because this is the second appearance of k, the term following this k must be 2k. Since multiples of t increment each time the next term must also be (w+1) × t. So then (w+1) × t = 2wt, meaning that w+1 = 2w, and then w = 1, a contradiction, since w ≥ 2.
Corollary 4.5: If k appears as consequence of Axiom 1 then all subsequent occurrences are also consequences of Axiom 1.
Note that none of this prevents any prior occurrences of k as consequence of Axiom 2. All we are showing here is that once there is an Axiom 1 occurrence, then all subsequent occurrences are Axiom 1, not Axiom 2.
Corollary 4.6: We can ascertain Q(k) precisely by calculating Q(d) : d | k : 1 < d < k. Hence, in generating the sequence and having produced A32742(k) = k/A20639(k) where A20639(k) is the least prime factor of k, we can calculate Q(k).
Theorem 5. Along with prime k (see Corollary 3.1), there are precisely 10 composite k that can only be produced by Axiom 1. These are listed in sequence C below:
C = {6, 9, 15, 25, 35, 49, 77, 121, 143, 169}.
Proof: Observe Corollary 2.2, i.e., 3 ∉ A. Also observe Table 5 concerning A607(p) for certain p. The behavior of A607(n) as n increases is well known: 17 is the fixed point such that for n > 17, A607(n) > n. Let us examine Axiom 2 (j × c( j) → k) regarding each of these 10 numbers.
p A607(p)
-----------
2 1
5 2
7 3
11 6
13 9
17 17
19 23
We note that all the numbers in C are semiprimes.
Squares:
9 = 3², requiring 3 3’s, but there are no 3’s in the sequence (see Corollary 2.2), hence Axiom 2 does not produce 9.
25 = 5²; we only have 2 in the sequence, hence Axiom 2 does not produce 25.
49 = 7²; A607(7) = 3 in the sequence, hence Axiom 2 does not produce 49.
121 = 11²; A607(11) = 6 in the sequence, hence Axiom 2 does not produce 121.
169 = 13²; A607(13) = 9 in the sequence, hence Axiom 2 does not produce 169.
Squarefree semiprimes:
6 has d × d' = {2×3, 3×2}, meaning we have 2 3’s or 3 2’s. There are no 3’s in the sequence, and A607(2) = 1, therefore Axiom 2 does not produce 6.
15 has d × d' = {3×5, 5×3}, meaning we have 3 5’s or 5 3’s. There are no 3's in the sequence, and A607(5) = 2, therefore Axiom 2 does not produce 15.
35 has d × d' = {5×7, 7×5}; we know we have too few 5’s or 7’s in the sequence, thus Axiom 2 does not produce 35.
77 has d × d' = {7×11, 11×7}; we know we have too few 7’s or 11’s in the sequence, thus Axiom 2 does not produce 77.
143 has d × d' = {11×13, 13×11}; we know we have too few 11’s or 13’s in the sequence, thus Axiom 2 does not produce 143.
Thus, we know Axiom 2 does not furnish k ∈ C; they are only brought about via Axiom 1, so Q(k) = q₁(k), that is, there are A607(k) copies of k in A, just as there are A607(p) copies of prime p in A.
Now, can we have other numbers in C?
Recall that Axiom 2 involves 2 factors, j and c( j), hence we are looking at pairs of divisors d × d' = k that both exceed 1 and are not equal to k. Though we cannot have certain p² = p × p because there are too few p’s in the sequence, we can have pε, ε > 2, because we instead can write these as p(ε−i) × pi or vice versa, with i ≥ 1. It is plain that we will have prime cubes such as 8 via 4 × 2, 27 via 9 × 3, 125 via 25 × 5, etc., and by iteration on the exponents of these primes we see that these largest proper divisors d = A32742(k) only grow larger, with A607(d) increasing accordingly.
Furthermore, products of more than 2 prime divisors have an even larger second-largest divisor d.
We have covered both increasing exponents of prime factors and increasing the number of distinct prime divisors, hence we have completed the proof. We cannot have other numbers in C because there is always at least 1 way to produce k through Axiom 2, namely, k/A32742(k) copies of A32742(k). So we are left with | C | = 10. ∎
Revisiting Corollary 4.2: For composite k ∈ C, we have j₂ = A32742(k). Therefore, we have 2 → 4, 4 → 8, 5 → 10, 6 → 12, etc., 11 → 33, 15 → 45, etc.
We might thus produce a table of numbers j that precede k like follows:
2: 2
4: 2 4
5: 5 6
6: 8 9
7: 7 10 12
8: 4 15 16 18
9: 14 20 24 27
10: 5 21 25 30 32 36
11: 11 28 40 45 48 54
12: 6 35 42 50 60 64 72 81
...
where figures in bold derive from Axiom 2 and the rest derive from Axiom 1.
Conclusion.
The inventory sequence is interesting in and of itself since it functions as a meta-sequence, cataloging its own content. The “payload” function ξ( j) = A1414( j) applied to novel j is of interest since it guarantees a finite number of copies of k, as will the extant condition j × c( j). The sequence reinterprets prime factors as partitions, and the predecessor and its cardinality as factors of other numbers.
We demonstrated the range of A353125 is ℕ \ {1, 3}. We have shown that the cardinality of k in A is finite, that is, Q(k) ≤ A607(k) + τ( j) − 2 via Corollary 4.1. Furthermore, if k is prime p, then the cardinality is exactly Q(p) = A607(p). This is true for certain composite k as a result of the properties of A607. These include the numbers in C = {6, 9, 15, 25, 35, 49, 77, 121, 143, 169}, which behave like primes as far as A353125 is concerned. As a result of the appearance of p yielding a second copy, primes p ≠ 3 appear for the first time and the second time immediately after, hence, all primes p appear in runs of length 2. We have shown through Corollary 4.4 that k appear as a result of Axiom 2, but then as a result of Axiom 1 as n increases, with no mixing. If composite k ∉ C, then we at least see the largest proper divisor A32742(k) → k via Axiom 2.
This concludes our examination..
Appendix.
Code 2 generates all auxiliary sequences. Such sequences describe major parameters of the sequence A.
Records r in A begin as follows:
2, 4, 8, 10, 14, 21, 24, 27, 36, 40, 50, 60, 72, 96, 120, 144, 168, 288, 432, 480, 576, 864, 1728, 2160, 2880, 5760, 6912, 7200, 10368, 11520, 20736, 21600, 25920, 43200, 51840, 57600, 69120, 86400, 103680, 138240, 172800, 207360, ...
The positions j such that A(j) = r for the first time begin as follows:
1, 3, 5, 9, 12, 17, 25, 27, 29, 33, 44, 56, 59, 62, 70, 75, 93, 97, 155, 184, 199, 204, 211, 295, 344, 392, 542, 557, 589, 659, 732, 840, 1017, 1038, 1253, 1323, 1469, 1536, 1586, 1697, 1771, 2448, 2581, 2610, 2635, 2846, 2948, 3056, ...
The list of distinct smallest missing numbers u in A begins as follows:
1, 3, 5, 9, 12, 17, 25, 27, 29, 33, 44, 56, 59, 62, 70, 75, 93, 97, 155, 184, 199, 204, 211, 295, 344, 392, 542, 557, 589, 659, 732, 840, 1017, 1038, 1253, 1323, 1469, 1536, 1586, 1697, 1771, 2448, 2581, 2610, 2635, 2846, 2948, 3056, ...
The sequence D of positions j such that A(j) = d = A56240(k) = k/A20639(k) for the first time begin as follows (see a text file of D(n), n = 1..2¹⁰):
0, 0, 0, 3, 0, 0, 0, 5, 0, 9, 0, 15, 0, 12, 0, 23, 0, 21, 0, 19, 17, 36, 0, 25, 0, 39, 27, 51, 0, 31, 0, 42, 49, 82, 0, 29, 0, 85, 64, 33, 0, 72, 0, 53, 120, 166, 0, 47, 0, 44, 146, 79, 0, 113, 115, 77, 141, 432, 0, 56, 0, 435, 159, 67, 106, 122, 0, 157, 233, 90, 0, 59, 0, 1113, 129, 163, 0, 111, 0, 104, 516, 1171, 0, 88, 172, 1174, 453, 144, 0, 137, 131, 252, 673, 1908, 195, 62, 0, 102, 772, 267, 0, 190, 0, 139, 180, 2795, 0, 109, 0, 297, 1147, 124, 0, 206, 346, 770, 161, 4080, 216, 70, 0, 3633, 1548, 713, 502, 243, 0, 100, 1897, 387, 0, 175, 222, 4203, 245, 231, 0, 357, 0, 301, 2096, 4597, 0, 75, 842, 4479, 282, 1168, 0, 327, 0, 273, 250, 417, 798, 236, 0, 5701, 2870, 135, 370, 299, 0, 1786, 504, 6657, 0, 93, 0, 261, 324, 1905, 0, 848, 597, 193, 4153, 7236, 0, 127, 0, 559, 4082, 429, 1183, 1040, 284, 2212, 376, 333, 0, 118, 0, 9979, 1571, 654, 0, 322, 0, 277, ...
We note that certainly, we write 0 for prime k and k ∈ {1, 6, 9, 15, 25, 35, 49, 77, 121, 143, 169}. From this data it appears we may search A(1..n) so as to guarantee √n terms of q₂.
The sequence q₂(k) appears below, where q₂(k) = 0 for prime k and k ∈ {1, 6, 9, 15, 25, 35, 49, 77, 121, 143, 169} (See a text file of q₂(n), n = 1..2¹²):
0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 2, 0, 1, 1, 1, 0, 2, 0, 2, 1, 1, 0, 3, 0, 1, 1, 2, 0, 2, 0, 2, 1, 1, 0, 3, 0, 2, 1, 2, 0, 2, 1, 2, 1, 1, 0, 5, 0, 1, 1, 2, 1, 3, 0, 2, 1, 2, 0, 4, 0, 1, 2, 2, 0, 3, 0, 3, 1, 1, 0, 5, 1, 1, 1, 2, 0, 4, 1, 2, 1, 1, 1, 5, 0, 2, 1, 3, 0, 3, 0, 3, 3, 1, 0, 4, 0, 2, 1, 4, 0, 3, 1, 2, 2, 1, 1, 6, 0, 1, 1, 2, 1, 5, 0, 3, 1, 2, 0, 4, 1, 1, 3, 3, 0, 3, 0, 5, 1, 1, 0, 6, 1, 1, 2, 2, 0, 5, 0, 3, 2, 3, 1, 4, 0, 1, ...
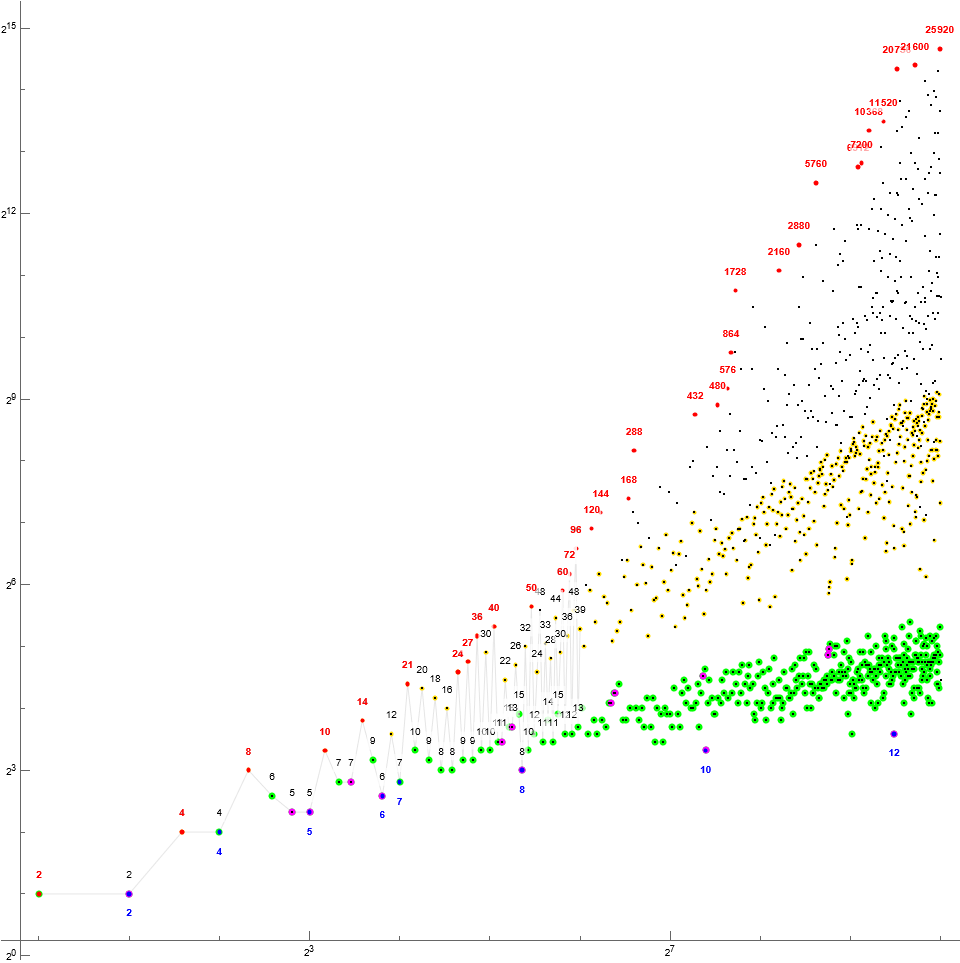
Figure 1: Annotated log-log scatterplot of A(n) for 1 ≤ n ≤ 210. Figures in red are records, blue local minima, green highlights novel successors, gold successors of novel successors.
References:
Code 1: Generate A and store it in the variable a353125:
a353125 = Block[{nn = 2^24, a, c, k, s}, c[_] = 0;
s = {2}; Table[(Set[a[i], #]; c[#]++) &@ s[[i]], {i, Length[s]}];
Monitor[Do[If[c[#] == 1,
Set[k, Total@ Flatten[ConstantArray[#1, #2] & @@@ FactorInteger[#]]],
Set[k, c[#] #]] &@ a[i - 1]; a[i] = k; c[k]++, {i, Length[s] + 1, nn}], i];
Array[a, nn] ];
Code 2: Generate auxiliary sequences.
a353125r = Union@ FoldList[Max, a353125] (* records *);
a353125ri = Block[{r = 1}, Reap[Do[If[# > r, r = #; Sow[i]] &@
a353125[[i]], {i, Length[a353125]}]][[-1, -1]]] (* positions of records *);
Set[{a353125u, a353125ui}, Block[{c, u = 4}, c[_] = 0;
Transpose@ Reap[Do[If[# == u, While[c[u] > 0, u++];
If[c[#] == 0, Sow[{u, i}]]] &@ a353125[[i]];
c[a353125[[i]]] = i, {i, 2^24}]][[-1, -1]]]]
(* smallest missing number and position *);
a353125v = Block[{nn = 2^20, a, c, k, s, v}, c[_] = 0;
s = {2}; v[1] = 0;
Table[(Set[a[i], #]; c[#]++) &@ s[[i]], {i, Length[s]}];
Monitor[ Do[If[c[#] == 1, Set[v[i], 0];
Set[k, Total@ Flatten[ConstantArray[#1, #2] & @@@ FactorInteger[#]]],
Set[{k, v[i]}, {c[#] #, 1}]] &@ a[i - 1];
a[i] = k; c[k]++, {i, Length[s] + 1, nn}], i];
Array[v, nn] ] (* axiom 1 = 0, axiom 2 = 1 *);
a056240 = {0}~Join~Import["https://oeis.org/A056240/b056240.txt", "Data"][[All, 1]]
(* A056240 = Smallest product of prime partitions of n *);
a353125di = Block[{nn = 2^10, a, c},
c = {1, 6, 9, 15, 25, 35, 49, 77, 121, 143, 169};
a = a353125[[1 ;; nn^2]];
Array[If[Or[PrimeQ[#], MemberQ[c, #]], 0,
FirstPosition[a, a056240[[#]]][[1]]] &, nn]]
(* first position of largest proper d | k *);
a353125q2 = Block[{nn = 2^20, c, s}, c[_] = 0; s = a353125[[1 ;; nn]];
Do[If[#1 < #2, c[#2]++] & @@ s[[i - 1 ;; i]], {i, 2, nn}];
Array[c, Floor[Sqrt[nn]]]] (* Axiom 2 cardinality of k *)
Code 3: Generate Figure 1.
Block[{kk = 2^6, nn = 2^12, a, r, s, t, u, v,
ss = {2, 4, 8, 14, 16, 41, 168, 715, 1910}, amber = Hue[1/7.]},
a = a353125[[1 ;; nn]];
r = Array[If[MemberQ[a353125ri, #], a[[#]]] &, nn];
s = Array[If[MemberQ[ss, #], a[[#]]] &, nn];
t = Array[If[a353125v[[#]] == 0, a[[#]]] &, nn - 1];
u = Array[If[a353125v[[# - 1]] == 0, a[[#]]] &, nn - 1];
v = {-1}~Join~Array[If[Total@ a353125v[[# - 1 ;; #]] == 0, a[[#]]] &, nn - 1, 2];
ListPlot[{a[[1 ;; kk]], t, u, v, a, r, s,
Array[Labeled[#, #, Top] &@ a[[#]] &, kk],
Array[If[IntegerQ[#], Labeled[#, #, Top, LabelStyle -> Directive[Bold, Red]]] &@ r[[#]] &, nn],
Array[If[IntegerQ[#], Labeled[#, #, Bottom, LabelStyle -> Directive[Bold, Blue]]] &@ s[[#]] &, nn]},
ImageSize -> 1440, AspectRatio -> 1, Joined -> Join[{True}, ConstantArray[False, 7]],
ScalingFunctions -> {"Log2", "Log2"},
PlotStyle -> {Directive[Gray, Thin],
Directive[Green, PointSize[Large]],
Directive[amber, PointSize[Medium]],
Directive[Magenta, PointSize[Large]],
Directive[Black, PointSize[Small]],
Directive[Red, PointSize[Medium]],
Directive[Blue, PointSize[Medium]], Transparent, Transparent, Transparent}] ]
Concerns sequences:
A000607: | λp(n) |, the number of prime partitions of n.
A001414: ξ( j) = ∑{p | k} p = ∑{i = Ω( j)} A027746( j, i), sum of prime factors of n with repetition.
A020639: least prime factor of n.
A032742: largest proper divisor d | n.
A056240: smallest m : ξ(m) = n. A056240(n) ≥ n with equality iff n = 4 or n prime.
A064364: T(n, A607(n)) ∋ ∪{ m : ξ(m) = n }.
Ex.: T(12) ∈ {35, 42, 50, 60, 64, 72, 81}, since
λp(12) ∈ {{7,5}, {7,3,2}, {5,5,2}, {5,3,2,2}, {3,3,3,3}, {3,3,2,2,2}, {2,2,2,2,2,2}},
∴ ∏ ↦ λp(12) = {35, 42, 50, 60, 64, 72, 81}.
A070824: = τ(n)−2, the number of nontrivial divisors of n.
A353125: Sequence A: A(1) = 2; if νA(1..n−1)( A(n−1)) = 1, ξ( A(n−1)), else A(n−1) × νA(1..n−1)( A(n−1)).
Document Revision Record.
2022 0508 2200 Draft.
2022 0509 1845 Final.