OEIS A356322
Michael Thomas De Vlieger, St. Louis, Missouri, 2022 1028.
Abstract.
Consider a partition of composite numbers into 3 mutually exclusive classifications A120944, A126706, and A246547, which we call “varius”, “tantus”, and “multus”, respectively [1]. In addition to these 3 composite classes, we consider the primes. There are 2 consecutive prime numbers {2, 3}. In 1844, Eugène Catalan conjectured that {8, 9} are the only consecutive multus numbers, the conjecture proved in 2002 by Preda Mihăilescu. Since 2² | m for m mod 4 ≡ 0, runs of consecutive varius numbers are limited to 1 ≤ ℓ ≤ 3, the smallest instance of ℓ = 3 is {33, 34, 35}. Among these, the run length of consecutive tantus numbers seems to be only bounded by prime gaps.
We propose A356332, the sequence of least m that start a run of at most ℓ consecutive tantus numbers, that is, numbers in A126706.
Introduction.
Let S = A126706 = { m : ω(m) > 1 ∧ Ω(m) ≠ ω(m) }, the sequence of “tantus” numbers, that is, numbers m that are neither prime powers nor squarefree. The sequence S begins as follows:
12, 18, 20, 24, 28, 36, 40, 44, 45, 48, 50, 52, 54, 56, 60, 63, 68, 72, 75, 76, 80, 84, 88, 90, 92, 96, 98, 99, 100, 104, 108, 112, 116, 117, 120, ...
Let T = A358089 be the first differences of S, that is, differences between consecutive tantus numbers. The sequence T begins as follows:
6, 2, 4, 4, 8, 4, 4, 1, 3, 2, 2, 2, 2, 4, 3, 5, 4, 3, 1, 4, 4, 4, 2, 2, 4, 2, 1, 1, 4, 4, 4, 4, 1, 3, 4, 2, 6, 3, 1, 4, 4, 3, 1, 2, 2, 1, 3, 4, 2, 2, 4, 3, 1, 3, 1, 4, 4, 4, 1, 3, 4, 2, 2, 4, 3, 1, 4, 4, 4, 4, 1, 3, 4, 2, 2, 4, 2, 2, 1, 3, 2, 2, 8, 1, 3, 4, 2, ...
We note that if such difference is 1, we have consecutive tantus numbers s, t such that t − s = 1. Observe that most of the smallest tantus numbers are singletons. We see that {44, 45} is the smallest instance of run length ℓ = 2, and that {98, 99, 100} is the smallest instance of ℓ = 3.
There are 4 consecutive tantus numbers m starting from 844 and again from 2888, but since 848 and 2892, respectively, are also in A126706, these m ascribe to ℓ = 5 instead. The range m = 3174…3177 has at most ℓ = 4 numbers in A126706 and 3174 is the smallest number with that quality, hence A356322(4) = 3174.
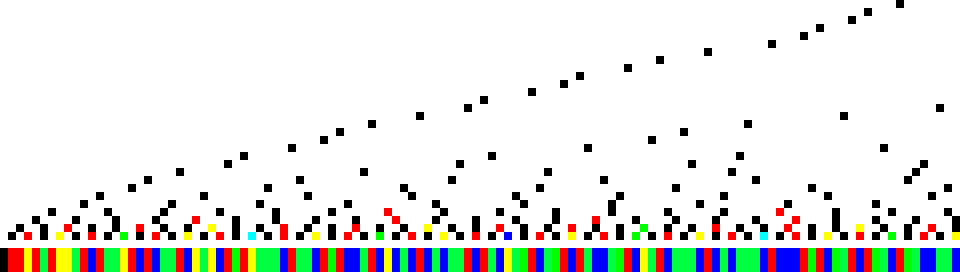
Figure 1 is a plot the prime power divisors pε | n for n = 1…120 at (n, π(p)) with a color function representing multiplicity ε, where black represents ε = 1, red ε = 2, … magenta represents the maximum value of ε (which is ε = 6 for n = 1…120). Under the graph, we place a stroke to denote the omega-multiplicity class of n, where black represents the empty product, red primes, yellow multus, green varius, and blue tantus numbers. We are concerned in this paper with tantus numbers represented by blue strokes. This figure represents the data in A126706 pictorially.
Using Code 1, we determine the following terms, starting with the trivial case of m = 12 for ℓ = 1:
12, 44, 98, 3174, 844, 22020, 217070, 1092747, 8870024
Remy Sigrist found 2 additional terms 262315467 and 221167422.
Conclusion.
Is there a limit to the number ℓ of consecutive tantus numbers? The question is tied to any limit to the length of prime gaps.
This concludes our examination.
Appendix.
j = 0; k[_] = False; Sort[Reap[Do[If[And[#2 > 1, #1 != #2] & @@ {PrimeOmega[n], PrimeNu[n]}, j++; If[! IntegerQ[c], Set[c, n]], If[j > 0, If[! k[j], Sow[{j, c}] ]; Set[{k[j], j}, {True, 0}]; Clear[c] ] ], {n, 2^16}] ][[-1, -1]] ][[All, -1]]
Concerns sequences:
A000961: Prime powers: for prime p, pε such that ε ≥ 0.
A001221: ω(n) = number of distinct prime divisors of n.
A001222: Ω(n) = number of prime divisors of n with multiplicity.
A001223: Prime gaps: differences between consecutive primes.
A005117: Squarefree numbers (union of primes and varius numbers).
A005250: Record gaps between primes.
A013929: Numbers that are not squarefree.
A024619: Numbers that are not prime powers.
A120944: Composite squarefree numbers (varius numbers).
A126706: Numbers neither squarefree nor prime power (tantus numbers).
A246547: Composite prime powers (multus numbers).
A356322: Least m that starts a run of at most n consecutive tantus numbers.
A358089: Tantus gaps: differences between consecutive tantus numbers.
References:
[1] M. De Vlieger, Omega multiplicity classes, Seq. Analysis, 18 May 2022.
Document Revision Record.
2022 1030 1500.