Omega Multiplicity Classes
18 May 2022.
Abstract.
We describe three nontrivial classes of composite number based on having 1 or many distinct prime divisors, and having at least 1 prime divisor with multiplicity greater than 1. These classes describe composite prime powers, composite squarefree numbers, and composites that are neither prime powers nor squarefree. We offer a bonus class that is a subset of composites that are neither prime powers nor squarefree.
New Terms for Classes of Composite Number.
Mathematics makes several distinctions among natural numbers n ∈ ℕ because many functions treat certain kinds of numbers in a predictable way. For instance, the divisor counting function τ(p) = 2 iff p is prime, but τ(n) > 2 for composite numbers, and τ(n) = 1 for the empty product n = 1. The Euler totient function φ(p) = p − 1 iff p is prime, etc. Squarefree numbers are products of distinct prime factors where each prime has multiplicity 1; 6 is squarefree since 6 = 2 × 3, but 12 is not squarefree since 12 = 2² × 3. Prime powers are numbers n = pε ; ε ≥ 0, a designation that includes 1 and the primes.
Let us divide the natural numbers n ∈ ℕ into 5 categories based on the number of primes p | n. We recognize that ω(n) is the number of distinct p | n, while Ω(n) is the number of p | n with multiplicity. The number n is said to be squarefree iff ω(n) = Ω(n). The number n is said to be prime iff ω(n) =Ω(n) = 1, and a prime power iff ω(n) = 1. The number n = 1, the empty product, in a category all to itself, therefore, we may hold that there are actually 4 nontrivial categories. We further distinguish numbers instead with M(n) = the largest multiplicity in n, meaning the largest exponent such that any prime power pε | n.
Therefore {n > 1} may be partitioned into numbers with ω(n) = 1 and those with ω(n) > 1, and then into those with M(n) = 1 and those with M(n) > 1. We might assign colors as handles for these categories, noting that the “red” (■) category ω(n) = M(n) = 1 of course corresponds with the primes.
Omega-Multiplicity Diagram
| M(n) = 1 | M(n) > 1 | |
| ω(n) > 1 |
|
|
| ω(n) = 1 | |
|
Therefore we have three categories of composite numbers that we shall assign names to, so as to be able to succinctly refer to them. The color codes are what is standard in this work whenever we need to refer to the aggregate kinds of natural numbers based on distinct prime factors and maximum multiplicity.
Multus numbers (■) are composite prime powers with ω(n) > 1 but M(n) = 1 and appear in OEIS A246547. The name derives from Latin multus, “many”, since we have many copies of the same primes p | n. The smallest multus number is 4. Examples of these are 16, 49, and 625. Subsets of A246547 are the squares of primes A1248, the cubes of primes A030078, etc.
Varius numbers (■) are composite squarefree numbers with ω(n) = 1 but M(n) > 1 and appear in OEIS A120944. The name derives from Latin varius, “variegated”, since we have a diverse set of distinct primes p | n, and only one copy (multiplicity) of any p. The smallest varius number is 6. Examples include 10, 77, and 2310. Subsets of A120944 include the primorials excepting {1, 2}, that is, A120944 = A2110 \ {1, 2}, and the squarefree semiprimes A6881, which are products of 2 dissimilar primes, e.g., 6, 10, 14, 15, etc. An obvious subset is the set of even semiprimes without the number 4, i.e., A100484 \ {4}.
Finally, tantus numbers (■) are composite numbers that are neither squarefree nor prime powers with both ω(n) and M(n) exceeding 1, and are listed in OEIS A126706. The name derives from Latin tantus, “so (many)”, since we have a diverse set of distinct primes p | n, and at least one prime p appears more than once, that is, the multiplicity of p in n is greater than 1. The smallest tantus number is 12; other examples are 36, 50, and 686. The highly composite numbers excepting {1, 2, 4, 6} are tantus, as well as the superior highly composite numbers. Therefore, A4490 \ {2, 6} ⊂ A2182 \ {1, 2, 4, 6} ⊂ A126706.
We might define a subset of tantus numbers for which for all prime divisors p | n, pε | n such that ε > 1. This is tantamount to the powerful numbers A1694 without prime powers A961, i.e., A1694 \ A961. We call these plenus numbers. Another way to think of plenus numbers is as a product of multus numbers.
We can define terms like “nonmultus” for numbers that are squarefree or tantus, that is, numbers that might be prime but not a prime power. Also, we may say “nontantus” numbers for those numbers that have either 1 distinct prime factor and any multiplicity, or are squarefree. Everyone is familiar with “nonprime” meaning 1 and the composites. We might also use the term “nonvarius” to mean nonsquarefree but including primes
It is clear that the prime powers A961 (■■) are a superset of prime and multus numbers. Squarefree numbers A5117 (■■) are a superset of prime and varius numbers. The so-called powerful (or squareful) numbers A1694 (■■) are a superset of multus and tantus numbers and {1}. OEIS A024619 (■■) is a superset of varius and tantus numbers. The composite numbers (■■■) comprise the multus, varius, and tantus numbers.
Some Properties.
The several types of positive integers presented here have application whenever we are making a distinction between divisors and nondivisors k in the cototient of n.
The totient T (or reduced residue system) mod n is the set of totatives of n. This means that for 1 ≤ k < n, gcd(k, n) = 1. That is, for k < n, k and n do not have a prime divisor in common. Hence, for n = 12, the totient is {1, 5, 7, 11} mod 12, or more succinctly {±1, ±5} mod 12.
The cototient is the complement {0…n−1 mod n} \ T, that is, all the numbers from 0 through n−1 except the totatives. Therefore, for n = 12, the cototient is {0, 2, 3, 4, 6, 8, 9, 10} mod 12, or more succinctly, {0, ±2, ±3, ±4, ±6} mod 12.
Primes p have a full totient, meaning that k ∈ {1…p−1 mod p} is coprime to p. The cototient is minimal and limited to numbers k ≡ 0 mod p, that is, multiples of the prime p.
Multus n = pm have a totient missing the divisors pε | n, 1 < ε < m, that is, {2…pm − 1} \ { pε : 1 < ε < m }. The cototient of multus numbers consists of divisors excepting 1, namely k ∈ { pε : 1 < ε < m } ∪ {n − pε : 1 < ε < m}. Example: the cototient of 8 is {0, 2, 4, 6} mod 8, or {0, ±2, ±4} mod 8.
Varius and tantus numbers n, that is, n such that ω(n) > 1, have a cototient fraught with multiples of prime divisors p | n. More specifically, the cototient of such n is the union of multiples mp for all p | n such that 0 ≤ mp < n. For example, the cototient of n = 60 includes multiples of 2, 3, and 5 in the cototient. This is {0, 2, 4, 6, ..., 56, 58}, ∪ {0, 3, 6, ..., 54, 57} ∪ {0, 5, 10, ..., 50, 55} = {0, ±2, ±3, ±4, ±5, ±6, ±8, ±9, ±10, ±12, ±14, ±15, ±16, ±18, ±20, ±21, ±22, ±24, ±25, ±26, ±27, ±28, 30} mod 60. Of course, the totient of 50 is more compact: {0, ±1, ±7, ±11, ±13, ±17, ±19, ±23, ±29} mod 60.
Let us plot the prime power divisors pε | n for n = 1…120 at (n, π(p)) with a color function representing multiplicity ε, where black represents ε = 1, red ε = 2, … magenta represents the maximum value of ε (which is ε = 6 for n = 1…120). Under the graph, we place a stroke to denote the omega-multiplicity class of n, where black represents the empty product, red primes, yellow multus, green varius, and blue tantus numbers.
Figure 1.
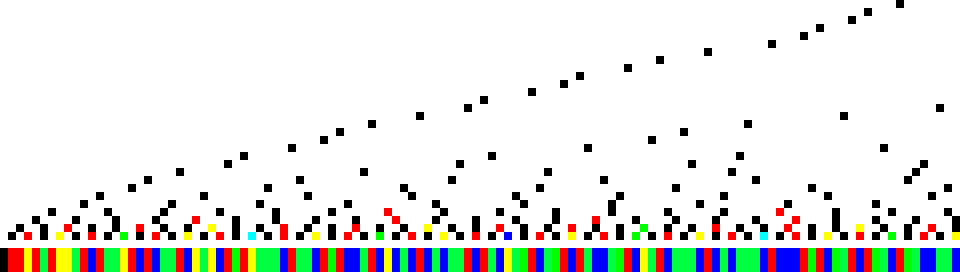
In such a graph, if we have a single black pixel above, we have a red stroke below, that is, a prime number. If we have a single colored pixel above, we have a yellow stroke below, denoting a multus number. If we have multiple black pixels in a column, we place a green stroke under the pixels, denoting a varius number. Finally, if we have more than 1 pixels with at least one in color, then we have a tantus number and a blue stroke below. We note the pattern of the omega-multiplicity classes. These are the subect of study in the briefs [1] and [2].
Conclusion.
The partitions named in this work aim to render a finer distinction to basic partitions of the composite numbers.
Appendix.
Concerns sequences:
A000961 The prime powers (union of primes and multus numbers).
A001221 ω(n) = number of distinct prime divisors of n.
A001248 Squares of primes (A1248 ⊂ A246547 multus numbers).
A001694 Powerful numbers (union of {1}, multus, and tantus numbers).
A002110 Primorials, products of the smallest k primes (A2110 ⊂ A120944 varius numbers).
A002182 Highly composite numbers (A2182 \ {1, 2, 4, 6} ⊂ A120944 varius numbers).
A002808 Composite numbers (union of multus, varius, and tantus numbers).
A004490 Superior highly composite numbers (A4490 \ {2, 6} ⊂ A120944 varius numbers).
A005117 Squarefree numbers (union of primes and varius numbers).
A006881 Squarefree semiprimes (A6881 ⊂ A120944 varius numbers).
A013929 Complement of squarefree numbers.
A024619 Numbers not prime powers (A120944 ∪ A126706, {m ∉ A961}).
A100484 Even semiprimes ({A100484 \ {4}} ⊂ A120944 varius numbers).
A120944 Composite squarefree numbers (varius numbers).
A126706 Numbers neither squarefree nor prime power (tantus numbers).
A246547 Composite prime powers (multus numbers).
A286708 Powerful numbers not prime powers (A1694 \ A961, plenus numbers).
References.
[1] M. De Vlieger, Omega multiplicity classes in the Ulam spiral and other arrangements. Seq. Analysis, 13 July 2022.
[2] M. De Vlieger, OEIS A356322: least m that begins a run of at least n consecutive tantus numbers. Seq. Analysis, 28 October 2022.
Document Revision Record.
2022 1030 1400.