Sycamore’s Once and Again Sequence
A sequence by David J. Sycamore of Mevagissey, England, UK.
written by Michael De Vlieger 17 December 2020.
Introduction.
Let s(1) = 1, and, if s(n) appears more than once in the sequence s, then s(n+1) is the number of terms in the sequence s that have appeared once, else s(n+1) is the number of terms that have appeared more than once.
This sequence s begins:
1, 1, 2, 1, 3, 2, 5, 2, 6, 3, 8, 3, 9, 4, 5, 11, 5, 12, 6, 14, 6, 15, 7, 8, 17, 8, 18, 9, 20, 9, 21, 10, …
s(2) = 1 since s(1) = 1, and there have only been a single 1 in s thus far, so we write 1 singleton.
s(3) = 2 since s(2) = 1, and we have 2 1s in the sequence, so we write 2 numbers seen more than once.
s(4) = 1 since s(3) = 2, because we have seen 1 more than once, but never have seen 2 before s(3).
s(5) = 3 since s(4) = 1, and we have seen 1 thrice, the number 1 being the only number so far seen more than once.
s(6) = 2 since s(5) = 3, and we have {2, 3} seen in the sequence just once.
s(7) = 5 since s(6) = 2, now that we have {1, 2} repeated thrice and twice, respectively, making 5 copies in all.
s(8) =
2 since s(7) = 5; we have {3, 5} seen in the sequence just once now.
s(9) = 6 since s(8) = 2, which is a copy, and in all we have three 1s and three 2s, making for 6 copies in all.
s(10) = 3 since s(9) has appeared once in the sequence right now, along with 5 and 6.
s(11) = 8 since s(10) is a copy. We have 3(1), 3(2), and 2(3), making 8 copies.
s(12) = 3 since s(11) is in {5, 6, 8}, appearing just once in the sequence.
s(13) = 9 since s(12) is a copy. We have 3 copies each of {1, 2, 3} now.
s(14) = 4 since s(13) has never before been seen, one of 4 such numbers, {5, 6, 8, 9} so far.
s(15) = 5 since s(14) is a number in {4, 5, 6, 8, 9} that have appeared only once thus far.
etc.
Figure 1 is a plot of (n, s(n)) for 1 ≤ n ≤ 45.
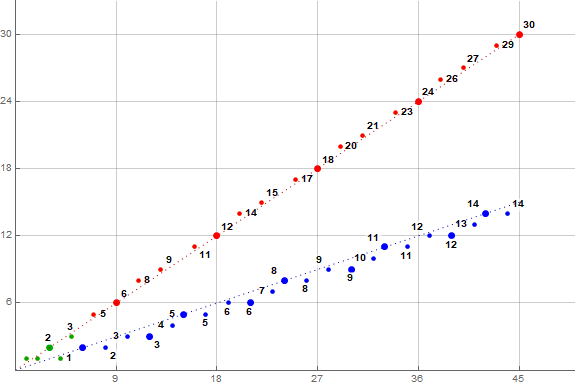
The plot in Figure 1 shows two distinct rays, an upper ray in red, and a lower ray in blue. The upper “pi” ray corresponds to the number π of terms seen more than once in s (instantiated at index n), and the lower “kappa” ray pertains to the number κ of terms seen once in s (instantiated at index n). Indeed, we could include s(n) for n in {1, 3, 5} with numbers seen once, and s(n) for even n < 5 with numbers seen more than once, but we color the first five terms green as they function as a preamble that sets up the pattern that sustains infinitely for n > 5. Therefore we have three segments; the green preamble sequence a(n) = {1, 1, 2, 1, 3}, the red pi-ray b(n) = π(n − 1) number of terms m that have appeared more than once, and the blue kappa-ray c(n) = κ(n − 1) number of terms m seen once (instantiated at n).
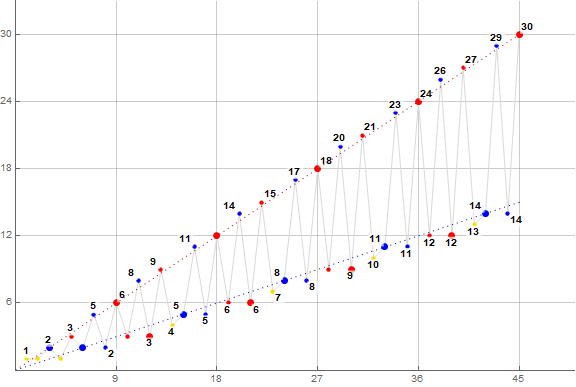
Figure 2 is a plot of (n, s(n)) for 1 ≤ n ≤ 45 color coded to show m ≡ 0 (mod 3) in large red, m ≡ 1 (mod 3) in medium gold, and n ≡ 2 (mod 3) in medium blue dots, joining the dots. Aside from m = 1, m ≡ 1 (mod 3) (which appear in medium gold) show only once in the sequence; the red and blue terms m appear thrice each.
Constructing the sequence from counting functions.
Let K represent the set of numbers m that appear just once in the sequence, instantiated at index n and let P represent the multiset of numbers m that have appeared more than once in the sequence, counting multiplicity. We may produce two counting functions κ(n) and π(n), the first counting terms that appear once (κάποτε) in the sequence, instantiated at index n, and the second (πολλοί) counting terms that have appeared more than once (the cardinality of the multiset of m appearing in n with multiplicity). Therefore, κ(n) = cardinality of the set K, and π(n) = cardinality of the multiset P.
We may define sequence s thus:
s(1) = 1, thereafter,
if s(n) appears once in s,
then s(n + 1) = κ(n),
else s(n + 1) = π(n).
(Formula 1)
The counting function κ(n) pertaining to numbers appearing once begins:
0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 8, 8, 8, 8, 9, 9, 9, 9, 10, 11, 11, 11, …
The first differences of κ(n) are:
0, 1, 0, 0, 0; 1, 0, 0, 0, 1, 0, 0, 0, 1, …
where the latter 9 terms repeat. Therefore κ increments by at most 1, and incrementation is back-to-back for n ≡ 4..5 (mod 9).
Whereupon we have a term m that appears once, we may see that the term occurs again as n increases, thus m is pulled from the set K of terms m that appear just once, instantiated at index n. We saw this for s(2) = 1, introducing a copy of the term m = 1, thus, removing 1 from the set K. The removals from K are transferred (with multiplicity) to the multiset P of terms m appearing multiple times in s. Thus, m having appeared once is an element of K, but when we have 2 instances of m, there are thus 2 copies of m in P, and m is removed from K. We see that, where 1 had appeared once in s for n = 2, since s(2) = κ(1) = 1, thereafter m = 1 no longer appears once, but we have 2 copies of 1 to report at s(3) = π(2) = 2 appears once; indeed, set K= {1} we are counting in κ(1) = 1 is not the same as set K = {2} that we count in κ(3) = 1.
We might see the sequence proceed according to n ≡ r (mod 9). The first 5 terms do not conform to the general pattern, as the introduction of s(2) = κ(1) = 1 initializes κ and s(3) = π(2) = 2 initializes π, pulling m = 1 from the set K and adding 2 copies of m = 1 in multiset P. At s(6) = 2, we have κ(6) = 2.
Table 1 shows the behavior of set K as n increases, when we report κ(n − 1) in sequences s.
n r κ K
-------------------------------------------------------------------
2 2 1 1
4 4 1 2
6 6 2 2 3
8 8 2 3 5
10 1 3 3 5 6
12 3 3 5 6 8
13 4 4 5 6 8 9
15 6 5 4 5 6 8 9
17 8 5 4 6 8 9 11
19 1 6 4 6 8 9 11 12
21 3 6 4 8 9 11 12 14
22 4 7 4 8 9 11 12 14 15
24 6 8 4 7 8 9 11 12 14 15
26 8 8 4 7 9 11 12 14 15 17
28 1 9 4 7 9 11 12 14 15 17 18
30 3 9 4 7 11 12 14 15 17 18 20
31 4 10 4 7 11 12 14 15 17 18 20 21
...
The first 5 terms of s stand apart from the “modular” portion of s as the conditions that give rise to modularity set up. Consider m mod 3. We might draw attention to singleton terms m ≡1 (mod 3) which persist indefinitely in K, and m belonging to 0 or 2 (mod 3) that are transient elements in K. Therefore we have two classes of elements in K; the singletons m ≡1 (mod 3) and transients m that are not congruent to 1 (mod 3).
The module commences at n ≡ 6 (mod 9). Here, for N = ⌊n/9⌋ > 0, we carry the transient elements from interval (N − 1), and add singleton m = 3N + 1. This is the first of 5 alterations to K in interval N. Each alteration adds 1 element to K.
n ≡ 6 (mod 9) adds the singleton m = 3N + 1,
n ≡ 8 (mod 9) adds the transient m = n − 3N, but we lost the least transient m = 3N + 2.
n ≡ 1 (mod 9) adds the transient m = n − 3(N − 1) + 1,
n ≡ 3 (mod 9) adds the transient m = n − 3(N − 1) + 1, again we lost the least transient m = 3N.
n ≡ 4 (mod 9) adds the transient m = n − 3(N − 1) + 1.
Therefore, in the interval we have the differences {1,0,1,0,1}. Therefore, generally, κ(9N + 1) = 3N.
The counting function π(n) pertaining to numbers appearing more than once begins:
0, 0, 2, 2, 3, 3, 5, 5, 6, 6, 8, 8, 9, 9, 9, 11, 11, 12, 12, 14, 14, 15, 15, 15, 17, 17, 18, 18, 20, 20, …
The first differences of π(n) are:
0, 0, 2, 0, 1; 0, 2, 0, 1, 0, 2, 0, 1, 0, …
where the latter 9 terms repeat. Therefore π increments by at most 2, and incrementation is back-to-back for n ≡ 4..5 (mod 9). The instances of incrementation by 2 represent the entry of a new m (as it requires the deposit of 2 copies in the multiset), whereas the incrementation by 1 represents an additional copy. Every distinct m in P eventually has 3 copies in the multiset, and the addition of any copy of m is permanent. We have no incrementation when the preceding term m has never appeared in s.
Table 2 shows the behavior of multiset P as n increases, when we report π(n − 1) in sequences s.
n r π P
----------------------------------------------------------
3 3 2 1.1
5 5 3 1.1.1
7 7 5 1.1.1 2.2
9 0 6 1.1.1 2.2.2
11
2 8 1.1.1 2.2.2 3.3
14 5 9 1.1.1 2.2.2 3.3.3
16 7 11 1.1.1 2.2.2 3.3.3 5.5
18 0 12 1.1.1 2.2.2 3.3.3 5.5.5
20 2 14 1.1.1 2.2.2 3.3.3 5.5.5 6.6
23 5 15 1.1.1 2.2.2 3.3.3 5.5.5 6.6.6
25 7 17 1.1.1 2.2.2 3.3.3 5.5.5 6.6.6 8.8
27 0 18 1.1.1 2.2.2 3.3.3 5.5.5 6.6.6 8.8.8
29 2 20 1.1.1 2.2.2 3.3.3 5.5.5 6.6.6 8.8.8 9.9
32 5 21 1.1.1 2.2.2 3.3.3 5.5.5 6.6.6 8.8.8 9.9.9
...
We see the numbers m that disappear from K appear here in duplicate, acquiring another copy in the next appearance of π(n − 1) in s.
n ≡ 7 (mod 9) adds 2 copies of m = 3N + 2,
n ≡ 0 (mod 9) adds a third copy of m = 3(N − 1) + 2, (which is the same number added in duplicate above),
n ≡ 2 (mod 9) adds 2 copies of m = 3N,
n ≡ 5 (mod 9) adds a third copy of m = 3N.
Aside from m = 1, the distinct m that appear in P belong to 0 or 2 (mod 3).
Therefore, in the interval we have the differences {2,1,2,1}. Hence, generally, π(9N) = 6N.
Conditional congruence relation for n > 5.
One thing to note is the occasion of numbers s(k) = 2k/3 for k ≡ 0 (mod 9). These terms are found in the upper (red) ray and define a line from origin of slope 2/3. Similarly, we find s(k) = k/3 for k ≡ 6 (mod 9), terms found in the lower (blue) ray. These hint at a congruence relation that we might use to describe the rays. Indeed we can write a conditional formula that produces the sequence for n > 5:
Formula 2:
s = {1, 1, 2, 1, 3} for 1 ≤ n ≤ 5;
For n > 5, if n mod 9 ∈ {0, 2, 4, 7}
then
s(n) = 2n/3 + (n mod 3)/3
else s(n) = n/3 − (n mod 3)/3
− [n ≡ 3 (mod 9)]
(Iverson brackets)
It seems clear that, outside of the first five terms (i.e., a(n)), we may calculate s(n) using the conditional congruence relation in Formula 1.
Indices n that are appearances of m in s(n).
Looking at Figure 2, immediately we see that, aside from m = 1, terms m ≡ 1 (mod 3) appear once, but any other m (including m = 1) appear thrice. If a term is repeated, it is indeed 3 times repeated. For triplicated m, we have one appearance followed by two appearances that have the separation in n of 2. This represents the entry of the duplicated lowest transient m in K into P, then the introduction of a new transient m = π(n − 1) into the set K. We shall differentiate between singleton 1 < m ≡1 (mod 3) that appear just once, and the transient, then eventually triplicated m belonging to 0 or 2 (mod 3), which moves from set K to multiset P as n increases.
We see singleton overtrine 1 < m ≡1 (mod 3) at the following indices:
(n, s(n)) = (3m + 2, m);
for m = 3k + 1, this is
(9k + 5, 3k + 1).
Triplicated m belonging to 0 or 2 (mod 3) have a more complicated appearance.
The trine term 5 ≤ m ≡ 0 (mod 3) appears thrice at the following indices:
(3m – (m mod 2))/2, 3m + 1, 3m + 3.
With m = 3k, we have:
(9k – (k mod 2))/2 , 9k + 1, 9k + 3.
The undertrine 5 ≤ m ≡ 2 (mod 3) appears thrice as follows:
(3m – (m mod 2))/2 – 1, 3m, 3m + 2.
With m = 3k – 1, we have:
(9k – ((3k – 1) mod 2) – 3)/2 , 9k – 3, 9k – 1.
Therefore, generally for nontrine m > 4 we have:
(3m – (m mod 2))/2 + (m mod 3) , 3m + 1 + (m mod 3), and 3m + 3 + (m mod 3),
the residue expressed as –1, 0, or +1 (mod 3).
We have m = 1 thrice at n = 1, 2, and 4.
The terms 2 ≤ m ≤ 3 appear thrice at indices 2m – 1 and again at 4m – 2 and 4m.
Hence we can predict any appearance of m.
This concludes the work in progress. More will be added soon.
Appendix:
Code 1: Generate s(n) per definition:
s = Block[{a = {1}},
Do[AppendTo[a, If[Count[a, a[[-1]] ] == 1,
Total@ Select[#, Last[#] == 1 &][[All, -1]],
Total@ Select[#, Last[#] > 1 &][[All, -1]]
] &@ Tally[a]], 2^12]; a]
Code 2: Generate s(n) via formula 2 (much faster):
s = {1, 1, 2, 1, 3}~Join~Array[
If[FreeQ[{0, 2, 4, 7}, #3],
(#1/3) - #2/3 - Boole[#3 == 3],
2 (#1/3) + #2/3
] & @@ {#, Mod[#, 3], Mod[#, 9]} &, 10^6, 6]
Code 3: Generate s(n) but report κ(n) at points when it changes:
Block[{a = {1}, k = {0}, kk = {}, kw = {0}, p = {0}, pp = {0}, pw = {0}},
Do[If[Count[a, a[[-1]] ] == 1,
(AppendTo[a, Total@ #[[All, -1]]];
AppendTo[k, Total@ #[[All, -1]]];
AppendTo[kk, i];
AppendTo[kw,
StringJoin@
Riffle[Map[ToString, Union@ #[[All, 1]]], "."]]) &@
Select[#, Last[#] == 1 &],
(AppendTo[a, Total@ #[[All, -1]]];
AppendTo[p, Total@ #[[All, -1]]];
AppendTo[pp, i];
AppendTo[pw,
StringJoin@
Riffle[Map[ToString,
Sort@ Flatten[ConstantArray[#1, #2] & @@ # & /@ #]],
"."]]) &@ Select[#, Last[#] > 1 &]
] &@ Tally[a], {i, 60}];
Array[{kk[[#]] - 1, Mod[kk[[#]] - 1, 9], k[[#]], kw[[#]]} &,
Length@ k - 1]] // TableForm
Code 4: Generate s(n) but report π(n) at points when it changes:
Block[{a = {1}, k = {0}, kk = {}, kw = {0}, p = {0}, pp = {0}, pw = {0}},
Do[If[Count[a, a[[-1]] ] == 1,
(AppendTo[a, Total@ #[[All, -1]]];
AppendTo[k, Total@ #[[All, -1]]];
AppendTo[kk, i];
AppendTo[kw,
StringJoin@
Riffle[Map[ToString, Union@ #[[All, 1]]], "."]]) &@
Select[#, Last[#] == 1 &],
(AppendTo[a, Total@ #[[All, -1]]];
AppendTo[p, Total@ #[[All, -1]]];
AppendTo[pp, i];
AppendTo[pw,
StringJoin@
Riffle[Map[ToString,
Sort@ Flatten[ConstantArray[#1, #2] & @@ # & /@ #]],
"."]]) &@ Select[#, Last[#] > 1 &]
] &@ Tally[a], {i, 60}];
Array[{pp[[#]] - 1, Mod[pp[[#]] - 1, 9], p[[#]], pw[[#]]} &,
Length@ p - 1]] // TableForm
Document Revision Record.
2020 1217 2200 Created.
2020 1218 1130 Indices n of terms m in s(n).