The One-by-One Sequence.
A sequence of David Sycamore.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0119.
Abstract.
...
Introduction.
We define a simple self-referential sequence a thus:
Let a(0) = 0. If the decimal expansion of a(n) = m contains the digit 1 then a(n+1) is the number c of 1s the sequence has seen so far. If a(n) contains no digit 1 then a(n+1) is the number k of terms m hitherto that have no digit 1. We are thus concerned with “oneful” and “oneless” terms m, granting a degree of onefulness (i.e., how many 1s there are in m) to store in c whereas a oneless term m merely increments k. (The sequence a is provisionally assigned the number S20210116.)
The sequence a begins:
0, 1, 1, 2, 2, 3, 4, 5, 6, 7, 8, 9, 10, 3, 11, 5, 12, 6, 13, 7, 14, 8, 15, 9, 16, 10, 11, 13, 14, 15, 16, 17, 18, 19, 20, 17, 21, 22, 18, 23, 19, 24, 20, 21, 25, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 26, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 27, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 28, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 29, 62, 63, 64, 65, 66, 67, 68, ...
Examples:
a(1) = 1 since the previous m = 0 is oneless, and there is 1 oneless term in the sequence.
a(2) = 1 since m = 1 is oneful; there is 1 digit one in the sequence.
a(3) = 2 since m = 1 is oneful and now there are 2 digits 1 in the sequence.
a(4) = 2 since m = 2, which is oneless, and there are 2 oneless terms in the sequence.
a(5) = 3 since m = 3 is oneless and there are now 3 oneless terms in the sequence.
etc.
We can write an auxiliary sequence a' that stores the number of ones in term a(n). When a(n) is oneless, a'(n) = 0. This sequence begins:
0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 2, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 2, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 2, 0, 3, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 2, 0, 1, 0, 2, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 2, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 2, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 2, 1, 1, 1, 1, ...
The sequence a' can be used to analyze the plot (n, a(n)).
Figure 1 is a plot of (n, a(n)) for 1 ≤ n ≤ 120, showing the oneless trajectory in red, and oneful in other colors, primarily green, representing m = 1 in green, m = 2 in blue:
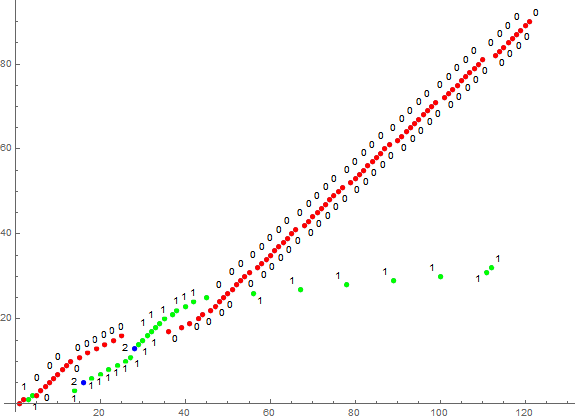
The plot is easy to interpret at this scale. The sequence a charges both registers. For 4 ≤ n ≤ 12, we have a run of oneless terms that represent the register k incrementing to k = 10. Whereupon k reaches the decimal rank 1 (i.e, log10 k = 1), c and k enter the sequence in a dithering fashion. For 25 ≤ n ≤ 34, the oneless register k is shut out as c enters a in the teens. We note a(26) = 11 which causes c to increase by 2 rather than 1. At a(35), with m = 22, the oneless k = 17 enters the sequence, dithering with the oneful c. Thereafter, we see the oneless register k dominate, only interrupted by any occasion of the digit 1 in the ones place of k. Notice the two green points (110, 31) and (111, 32), the result of c happening to contain a 1 in the ones place and doubling up.
Hence we can see that the dynamics of the occasion of digits 1 in the registers c and k are the source of a sort of braiding interaction between the oneful and oneless trajectories.
Figure 2 is a plot of (n, a(n)) for 1 ≤ n ≤ 1024, showing the oneless trajectory in red, and oneful in other colors, primarily green, representing m = 1 in green, m = 2 in cyan, and m = 3 in blue:
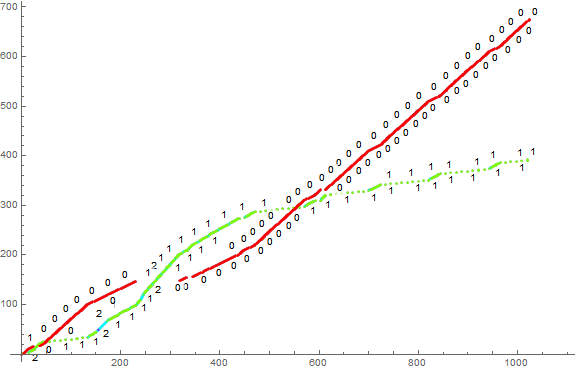
The plot exhibits a braided “double helix” effect, including the complete supression of oneless numbers for an interval for each decimal rank commensurate to the decimal expansion of m beginning with the digit 1. Hence we expect the oneless trajectory to be interrupted for a span of 10r terms in each decimal rank r.
Figure 3 is a log-log plot of (n, a(n)) for 1 ≤ n ≤ 220 with the oneless trajectory in black and the oneful trajectory color coded to represent the degree of onefulness:
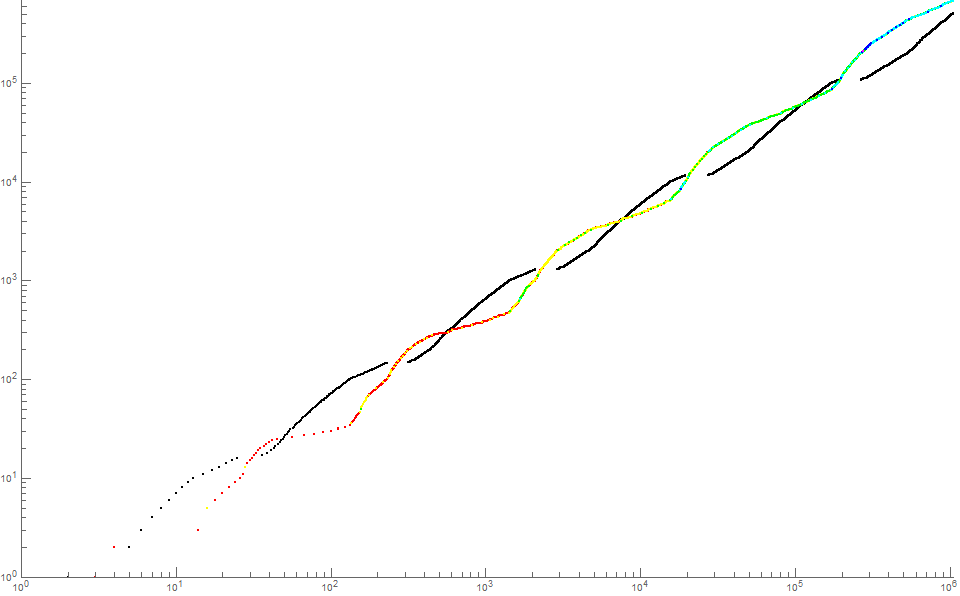
Table 1 lists the places where trajectories cross:
i n a(n)
---------------------
1 3 c 1
2 4 k 2
3 34 c 17
4 44 k 22
5 296 c 148
6 502 k 251
7 2584 c 1292
8 5974 k 2987
9 23256 c 11628
10 110575 k 60743
11 214838 c 107419
...
Decoupling of the trajectories.
It seems clear that the two trajectories will continue their irregular alternations ad infinitum, however, since c advances according to the degree of onefulness while k increments according to the fact of onelessness, we expect that there should be a point where the trajectories no longer cross, and the oneful trajectory is always above the oneless. This point could already have been observed, or it may be observed given another decimal rank of terms (that is, between the millionth and ten-millionth term).
We might elect to study this sequence in different bases. Usually, the simplest case of a sequence involving digits brings us to binary notation, however, we note that a binary number n expressed in standard form must begin with the digit 1 for n > 0. Hence the simplest base we might study is ternary.
Figure 4 is a plot of a3(n) for 1 ≤ n ≤ 1024, with the oneless trajectory in red and the oneful trajectory generally in green, but using a color function to signify the degree of onefulness.
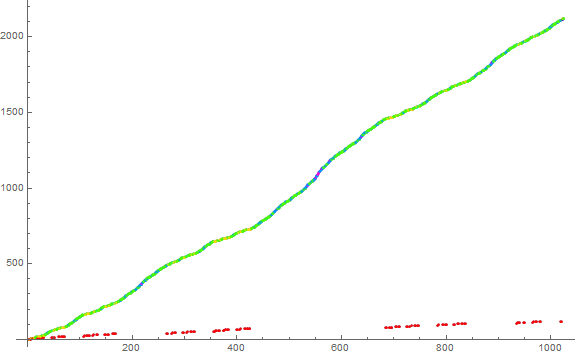
The trajectories have decoupled quite early at a3(7), with the oneful trajectory heavily boosted by the degree of onefulness.
Figure 5 is a log-log plot of a6(n) for 1 ≤ n ≤ 4096, again showing oneless trajectory in red and oneful generally in green, but using a color function to signify the degree of onefulness.
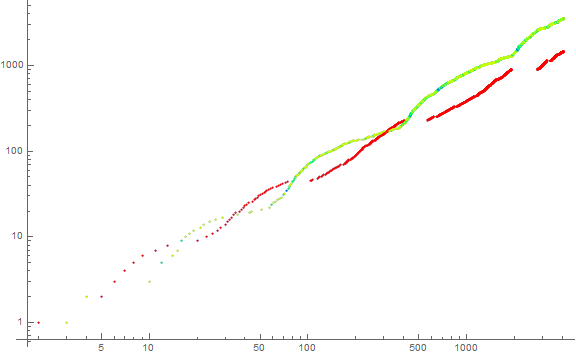
This plot resembles Figure 3, however we witness the decoupling of the two trajectories at a6(418).
Hence we expect the decimal case to decouple given the fact that, upon activation, the oneful trajectory is boosted as to the degree of onefulness, whereas the oneless case is only incremented.
The braided appearance of the plot of a(n) attained given 1048576 terms is thus still only a premature phase.
Variant.
We define a variant of this sequence thus:
b(0) = 0. Thereafter, if b(n) = m contains the digit 1 then b(n+1) is the number of 1s the sequence has seen so far. If b(n) contains no digit 1 then b(n+1) is the number of terms m seen thus far that have no digit 1.
This sequence begins:
0, 1, 1, 2, 2, 3, 4, 5, 6, 7, 8, 9, 10, 3, 12, 4, 14, 5, 16, 6, 18, 7, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100, 8, 103, 9, 106, 10, 11, 13, 14, 15, 16, 17, 18, 19, 20, ...
Again, we might identify the provenance of the terms using a sidecar sequence or record the register values of the oneless (k) or oneful (c) terms.
(Work in progress.)
Appendix:
...
Code 1: Generate the first 120 terms m in a(n):
Block[{a = {0}, c = 0, k = 0},
Do[If[# == 0, k++; AppendTo[a, k], c += #; AppendTo[a, c]] &@
DigitCount[a[[-1]], 10, 1], 120]; a]
Document Revision Record.
2021 0119 2215 Draft 1.
2021 0120 1815 Draft 2.