The Exceeding-Spacing Sequence.
A sequence of David Sycamore.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0208.
Abstract.
We consider a conditional self-referential integer sequence a = s20210203 that, starting with a(1) = 1 and upon seeing the most current term m already in a, we enter how long ago we last saw m, otherwise, we enter the number of terms seen that are larger than m.
Introduction.
Let a(1) = 1, and if m = a(n) is in the sequence more than once, then a(n + 1) = n − k + j with j = −1 and a(k) = m the immediately previous occurence of m, else a(n + 1) = c, with c the number of terms a(k) > a(n) for 1 ≤ k ≤ n.
The sequence begins:
1, 0, 1, 1, 0, 2, 0, 1, 3, 0, 2, 4, 0, 2, 2, 0, 2, 1, 9, 0, 3, 11, 0, 2, 6, 2, 1, 8, 2, 2, 0, 7, 3, 11, 11, 0, 4, 24, 0, 2, 9, 21, 1, 15, 2, 4, 8, 18, 2, 3, 16, 3, 1, 9, 12, 5, 16, 5, 1, 5, 1, 1, 0, 23, 1, 2, 16, 9, 13, 8, 22, 2, 5, 12, 18, 26, 0, 13, 8, 8, 0, 3, 29, 0, 2, 12, 11, 51, 0, 4, 43, 1, 26, 16, 26, 1, 3, 14, 17, 12, 13, 22, 30, 2, 18, 29, 22, 4, 17, 9, 41, 2, 7, 80, 0, 25, 10, 39, 4, 10, ...
Code 1 generates the sequence. Click here for a text file containing 216 + 1 terms.
a(2) = 0 because a(1) = 1 has never before appeared in a, hence we see 0 terms greater than a(1) currently in the sequence.
a(3) = 1 since 0 has appeared for the first time and there is 1 term (1) larger than 0.
a(4) = 1 since 1 is in the sequence more than once and the last occurence of 1 appears with 1 term between its penultimate and ultimate occurence.
a(5) = 0 since 1 is in the sequence multiple times and the last occurrence happened with 0 interposing other terms.
a(6) = 2 since 0 appears more than once and the penultimate and last occasions of 0 have 2 interposing terms.
a(7) = 0 since 2 has never appeared and there aren’t any terms in a larger than 2.
a(8) = 1 since 0 has appeared many times and the last occasion of it is 1 term back from this last entry of 0 in the sequence.
a(9) = 3 since 1 appears 3 terms back.
a(10) = 0 since 3 has never appeared and sets a record.
a(11) = 2 since 0 appears 2 terms back.
a(12) = 4 since 2 appears 4 terms back, etc.
We observe that there are plenty of zeros in the sequence. There are two sources of a(n+1) = 0 in sequence a:
- a(n) sets a record, meaning that a(n) is both unprecedented, and consequently, hitherto, there are no greater terms in a,
- a(n) appears consecutively.
Repeated values of m in a(n) for 1 ≤ n ≤ 216 occur as follows. These values are duplicated but none have been found to be repeated further.
Table 1: repeated values in the sequence. Each duplication is followed by 0.
i n a(n)
-----------------
1 3 1
2 14 2
3 29 2
4 34 11
5 61 1
6 79 8
7 384 3
8 551 17
9 558 3
10 718 50
11 823 14
12 1304 195
13 1424 51
14 1712 35
15 2272 375
16 6328 30
17 6465 51
18 9781 1468
19 12294 909
20 12714 284
21 13033 225
22 15813 217
23 18623 1
24 38923 741
...
Given 65536 terms, there are 144 zeros; 1 out of 6 of these is generated by duplication of m.
The records transform r of a begins:
1, 2, 3, 4, 9, 11, 24, 26, 29, 51, 80, 100, 101, 116, 145, 155, 156, 167, 217, 228, 230, 270, 271, 299, 317, 346, 448, 449, 570, 589, 607, 656, 800, 876, 878, 1142, 1150, 1205, 1222, 1248, 1388, 1426, 1679, 1704, 1842, 2101, 2120, 2145, 2510, 2672, 2721, 2832, 3137, 3253, 3305, 3564, 3658, 3844, 4047, 4138, 4514, 4537, 4831, 5415, 6080, 7047, 7133, 7595, 7904, 8168, 8204, 9296, 9548, 10070, 10143, 10175, 10965, 11528, 12600, 13505, 13774, 14100, 15195, 16613, 16862, 17193, 17524, 20104, 21403, 23470, 23740, 24044, 25289, 26411, 27715, 28299, 28317, 29154, 29893, 30137, 30496, 31356, 34153, 38823, 42084, 42393, 44043, 44306, 44452, 44981, 45336, 46327, 47611, 49303, 49947, 50408, 52187, 52448, 54909, 55710, 56755, ...
These appear at indices n:
1, 6, 9, 12, 19, 22, 38, 76, 83, 88, 114, 127, 147, 182, 189, 195, 249, 263, 322, 355, 359, 388, 486, 490, 548, 556, 591, 604, 686, 801, 829, 904, 997, 1096, 1255, 1377, 1531, 1595, 1649, 1701, 1893, 1903, 2036, 2185, 2380, 2523, 2726, 2954, 3068, 3293, 3478, 3831, 3861, 4306, 4349, 4414, 4528, 5072, 5208, 5297, 5664, 5668, 5837, 6051, 6568, 8117, 8599, 9270, 9649, 9918, 10859, 10862, 11289, 11714, 12588, 12677, 12874, 14159, 14254, 15764, 15863, 16794, 17489, 18264, 18810, 19722, 20252, 21230, 23947, 24994, 27068, 27405, 29605, 29922, 31245, 31922, 33053, 34453, 35274, 36988, 37027, 37119, 37616, 42686, 45176, 49169, 49916, 50276, 54106, 54909, 55844, 55963, 56353, 56619, 57959, 59298, 59605, 60142, 60886, 65341, 65537, ...
Figure 1 is a plot of a(n) for 1 ≤ n ≤ 28, showing zeros in blue and records in red:
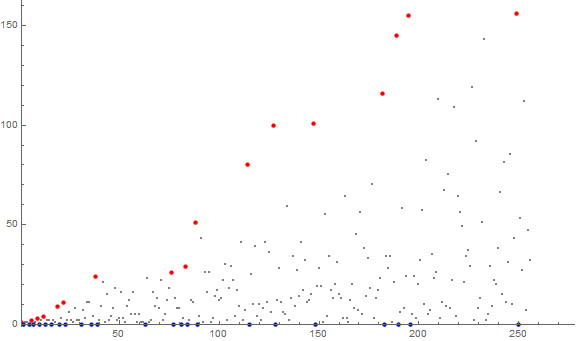
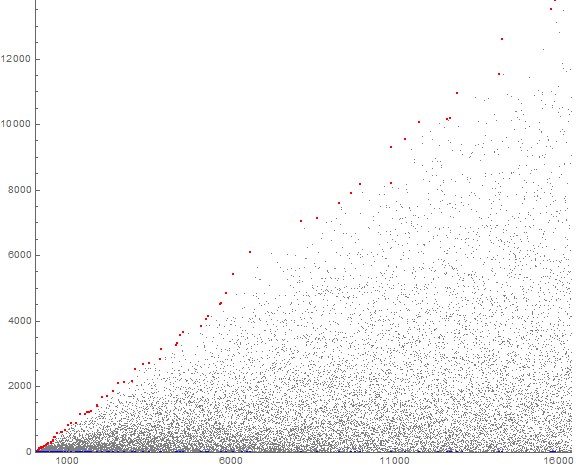
Figure 2 is an extended plot of a(n) for 1 ≤ n ≤ 214, showing zeros in blue and records in red (click here for an extended log-log plot of a(n) for 1 ≤ n ≤ 216):
We may trace the generative provenance of a(n), that is, mark and annotate a(n) with the progenitor m = a(n − 1).
Figure 3 is a plot of a(n) for 1 ≤ n ≤ 26, the color function and label indicating the previous term a(n − 1) (click here for an extended plot of a(n) for 1 ≤ n ≤ 214):
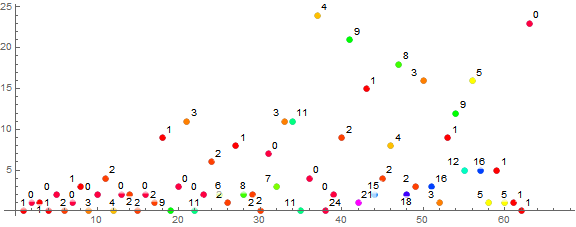
The extended plot supports the notion that the most-often seen m occupy the higher register of the plot, while novel values m languish near the bottom. We know that record m is followed by 0, but new m tends to be followed by a small m', since novel m tends to be relatively large if not a recordsetter.
This induces us to examine the least unused number m, recorded at u(n). The sequence of unused numbers u undergoes episodic change, hence we can take primitive terms M in a sequence of such, U, and thereby make a list of the first appearances of these primitive least unused numbers.
Table 2 lists the primitive least unused numbers and the index n were this least unused number first appears:
i u(n) n
-----------------
1 0 1
2 1 2
3 2 3
4 3 6
5 4 9
6 5 12
7 10 56
8 19 117
9 20 149
10 31 158
11 33 159
12 35 175
13 37 207
14 40 225
15 69 579
16 77 699
17 110 926
18 127 1245
19 128 1252
20 226 2581
21 245 2631
22 247 2997
23 250 3667
24 273 4108
25 381 7182
26 604 9520
27 674 12089
28 759 13186
29 833 15127
30 919 17714
31 1179 24629
32 1500 27168
33 1576 31403
34 1703 32591
35 1744 33172
36 1890 40377
37 2128 45404
...
We may also examine the conditional provenance of a(n). We determine whether a(n) has appeared before in the sequence or not. Let b(n) = 0 if a(n) never appeared in a, else b(n) = 1.
The occasion of b(n) = 0 therefore pertains to novel m.
Though a is not a permutation of the natural numbers on account of the repetition or recurrence of m, we see that u(n) represents a threshold under which all m are in a(n) for 1 ≤ n. We look to m' = a(n + 1) whose progenitor is novel m at a(n). Generally these m' tend to be relatively small, certainly outside of the given a(1), never set records. If novel m did not set a record, the condition requires enumeration of previous values exceeding m, and we have observed that least unused u(n) is small compared to the records in a(n) as n increases, and proportionally loses ground). Therefore we are precluded from a large “head” of larger values, since necessarily, novel m ≥ u(n). The larger the new m, the smaller the value of m'. As a consequence, m' is never large. Observationally, we may find a series of records in the numbers m' resulting from novel m and these prove to amount to around half the size of the records in sequence a itself, for 1 ≤ n ≤ 216. Most novel m instigate m' < u(n).
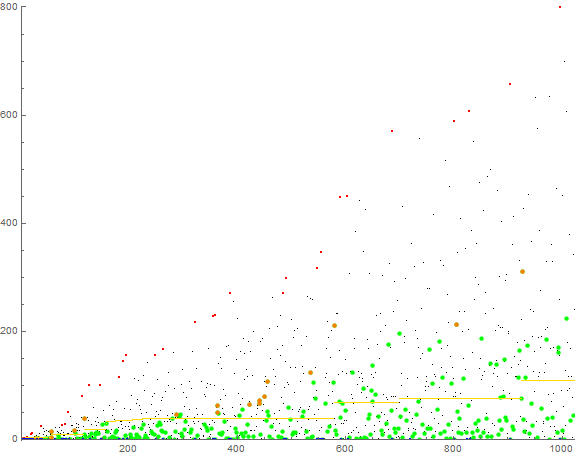
Figure 4 is a plot of a(n) for 1 ≤ n ≤ 210, with records in small red and zeros in small blue, the m = a(n + 1) attributable to novel a(n) in green, with recordsetters in orange, also indicating least unused m in yellow. (Click here for an extended plot of a(n) for 1 ≤ n ≤ 216):
Variants of a(n).
We have considered a variant of a that considers the “spacing” of the last two occasions of m when m has already appeared in a, hence with j = −1. Consider this variant a−1, and also consider a0 with j = 0 and a+1 with j = +1.
As we’ve seen, a−1 begins:
1, 0, 1, 1, 0, 2, 0, 1, 3, 0, 2, 4, 0, 2, 2, 0, 2, 1, 9, 0, 3, 11, 0, 2, 6, 2, 1, 8, 2, 2, 0, 7, 3, ...
Variant a0 begins:
1, 0, 1, 2, 0, 3, 0, 2, 4, 0, 3, 5, 0, 3, 3, 1, 13, 0, 5, 7, 1, 5, 3, 8, 1, 4, 17, 0, 10, 2, 22, 0, 4, ...
Finally, a+1 begins:
1, 0, 1, 3, 0, 4, 0, 3, 5, 0, 4, 6, 0, 4, 4, 2, 8, 0, 6, 8, 4, 7, 2, 8, 5, 17, 0, 10, 1, 27, 0, 5, 8, ...
These sequences have somewhat comparable terms for 1 ≤ n ≤ 16, but thereafter the sequences’ behaviors differ in a complex way.
Figure 5 is a plot of a0(n) for 1 ≤ n ≤ 210 in the character of Figure 4 which pertains to a−1(n).
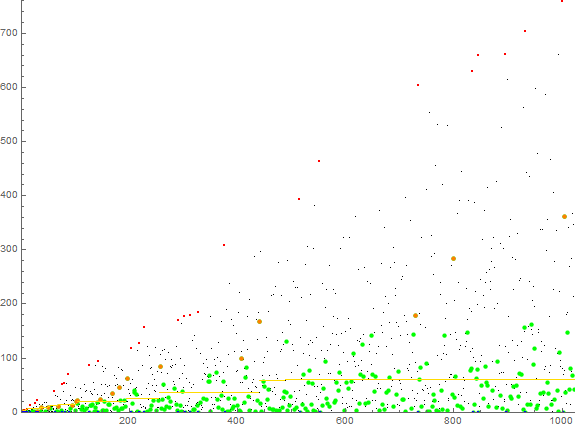
Figure 6 is a plot of a+1(n) for 1 ≤ n ≤ 210 in the character of Figure 4 which pertains to a−1(n).
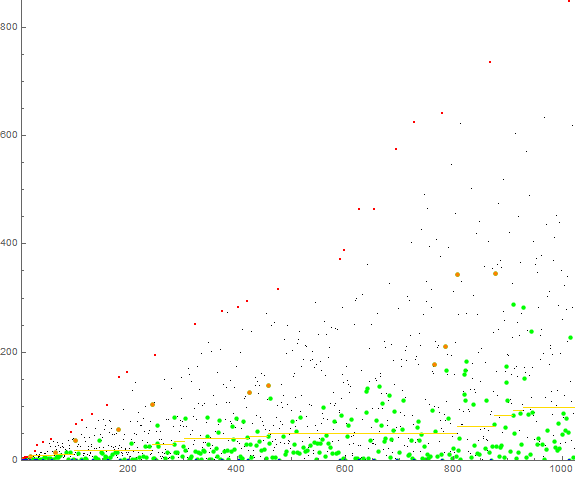
We see that these variations do not seem to markedly change the general behavior observed for sequence a−1. The variant a−1 is perhaps preferable over the others because we have two means by which we obtain zeros, whereas we only obtain zeros in the other two via recordsetters.
Further consideration suggests that we might regard a seed (i, j) where i is the first term of the sequence and j the spacing. Therefore we have considered (1, −1), (1, 0), and (1, 1). We might also consider (0, 0).
We might also consider the Van Eck sequence (OEIS A181391) a related self-referential conditional sequence. Let condition 0 pertain to unprecedented m while condition 1 applies to m already in the sequence. We may regard the Van Eck sequence as a singly-self-referential sequence as novel m instigate the following constant term 0, whereas a(0,0)(n) assigns a self-referential function to the succeeding term. We shall examine the case of a(0,0)(n) in the context of the Van Eck sequence in an upcoming paper.
This concludes our examination.
Appendix:
Block[{a = {1}},
Do[If[FreeQ[Most@ a, a[[-1]] ],
AppendTo[a, Count[Most@ a, _?(# > a[[-1]] &)]],
AppendTo[a, FirstPosition[Reverse@ Most@ a, a[[-1]] ][[1]] - 1 ] ], {i, 120}]; a]
Code 2: Plot a−1(n) in the style of Figure 4:
Block[{nn = 2^10, a = {1}, b = {0}, c, d = {1}, k, o = -1, r, s, t, u = {0}, w, z, out = -100},
w = Range[nn];
Do[If[FreeQ[Most@ a, a[[-1]] ],
AppendTo[a, Set[k, Count[Most@ a, _?(# > a[[-1]] &)]]];
d = Union[d, {k}]; AppendTo[b, 0]; w = DeleteCases[w, k];
AppendTo[u, First[w]],
AppendTo[a,
Set[k, FirstPosition[Reverse@ Most@ a, a[[-1]] ][[1]] + o]];
d = Union[d, {k}]; AppendTo[b, 1]; w = DeleteCases[w, k];
AppendTo[u, First[w]] ];, {i, nn}];
c = Array[a[[#]] (1 - b[[#]]) &, Length@ a];
r = Map[FirstPosition[a, #][[1]] &, Union@ FoldList[Max, a]];
r = Array[If[FreeQ[r, #], out, a[[#]]] &, nn];
s = Array[If[b[[#]] == 0, a[[#]], out] &, nn];
t = Map[FirstPosition[c, #][[1]] &, Union@ FoldList[Max, c]];
t = Array[If[FreeQ[t, #], out, a[[#]]] &, nn];
z = Array[If[a[[#]] == 0, a[[#]], out ] &, nn];
ListPlot[{a[[1 ;; nn]], s, r, t, u, z}, ImageSize -> Large,
PlotRange -> {{1, nn}, {-1, Max@ a[[1 ;; nn]]}},
AspectRatio -> Automatic,
PlotStyle -> {
Directive[Black, PointSize[Tiny] ],
Directive[Green, PointSize[Medium] ],
Directive[Red, PointSize[Small] ],
Directive[Orange, PointSize[Medium] ],
Directive[Hue[1/7], PointSize[Tiny] ],
Directive[Blue, PointSize[Small] ]
}]
]]
Document Revision Record.
2021 0208 1800 Created.
2021 0209 1000 Renamed, concluding paragraph added.