The Overxeroxed Sequence.
A sequence of David Sycamore.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0301.
Abstract.
We examine a conditional self-referential integer sequence that exhibits complementary counting functions as two subsidiary conditions based on novelty of the previous term. Hence the sequence effectively possesses a tripartite conditional approach to self-construction. The counting functions manifest as definite streams in the scatterplot that, via the extant-instigated condition, echo in a noisy way, making for an interesting plot.
Introduction.
We examine the conditional self-referential sequence S20210228 = a defined as follows:
Let m be a distinct or primitive term in a.
a(1) = 0; if a(n) is novel m in a, then, if m is prime, a(n+1) = c, the number of primes in a(k) for 1 ≤ k ≤ n, otherwise, m is nonprime, hence a(n+1) = n − c; else a(n) is an extant m last appearing at a(k), hence a(n+1) = n − k.
The sequence a begins:
0, 1, 2, 1, 2, 2, 1, 3, 4, 5, 5, 1, 5, 2, 8, 7, 9, 8, 3, 11, 11, 1, 10, 11, 3, 6, 12, 13, 15, 14, 15, 2, 18, 17, 17, 1, 14, 7, 22, 20, 21, 22, 3, 18, 11, 21, 5, 34, 26, 27, 28, 29, 23, 24, 30, 31, 25, 32, 33, 34, 12, 34, 2, 31, 8, 47, 28, 16, 40, 41, 29, 19, 31, 9, 57, 43, 33, 18, 34, 17, 45, 47, 16, 15, 53, 36, 50, 51, 52, 53, 5, 44, 54, 55, 56, 57, 21, 51, 10, 76, 62, 63, 64, 65, 66, 67, 39, 68, 69, 70, 71, 40, 43, 37, 42, 73, 43, 4, ...
Conditional structure of a.
There are 3 practical conditions, to which we assign labels.
- Condition −1 pertains to novel nonprimes m wherein we do not increment c, and enter a(n+1) = (n − c).
- Condition 0 pertains to novel primes m wherein we increment c and enter a(n+1) = c.
- Condition +1 pertains to extant or reiterated m (already in a), last appearing at a(k). If m is prime we must increment c but we do not report it. We merely enter a(n+1) = (n − k). We could consider Condition +1 instead as two separate conditions, however, the directly sensible effect of the condition is the entry of the difference (n – k). Indeed, the subtle effect is the unreported incrementation of the sequence’s prime counting function c.
Conditions −1 and 0 arise from novel m, while Condition +1 arises from extant m. However, the counting function c or (n − c) selected via novel primality introduces a second subsidiary condition, whereas the extant condition merely computes distance (n − k) to the penultimate instance a(k) of m. Hence, the two counting functions mount regardless of the novel or extant condition.
Hence we can write a sequence b(n) that registers the condition instigated by a(n−1). This sequence begins:
-1, -1, 0, 1, 1, 1, 1, 0, -1, 0, 1, 1, 1, 1, -1, 0, -1, 1, 1, 0, 1, 1, -1, 1, 1, -1, -1, 0, -1, -1, 1, 1, -1, 0, 1, 1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, -1, -1, -1, -1, 0, 0, -1, -1, 0, -1, -1, -1, 1, ...
Generally, the counting function c and the difference (n − c) generate prominent striations in the plot of a(n), since c increments upon any occasion of novel or extant prime.
The algebraic difference function (n − k) is a source of “randomization” or scatter in the plot, and also the “feedback” features seen in the scatterplot of a(n).
The least unused m.
Clearly, a(n) < n since c + (n − c) = n, and (n − k) ≥ 1.
The sequence a is not a permutation of natural numbers since a(1) = a(3) = 1. There are three sources for a particular m; through the prime counting function c or the nonprime counting function (n − c), finally, via (n − k). The first two sources, once they have exceeded m as n increases, no longer serve as a means to deliver m, yet there is no prohibition against (n − k) = m for 1 ≤ m ≤ (n − 2).
We can identify the least m that does not appear in the sequence in the first n terms. Another way to examine this problem is to find the least index n where m is found, thus, write an auxiliary sequence such that w(m) = n. Then we find the records m in w.
The first 5 records are also records in a, which shows that a is solidly populated for a finite time, until we find ourselves missing m = 6. In fact, a is covered by 1 ≤ m ≤ 5 for 1 ≤ n ≤ 14. Thereafter, the least missing m (which we shall call u) increases fairly slowly. We see that the least missing m = 12 and 13 also derive from records and Condition −1.
Table 1 lists u and the index n where u first enters a. Asterisked u signify record-setting u, meaning that the sequence a is completely covered at index n.
u n
------------
1* 2
2* 3
3* 8
4* 9
5* 10
6 26
12* 27
13* 28
14 30
16 68
19 72
35 1842
38 5609
181 224404
864 ?
For n = 13, c = 7, hence we see that obtaining u = 6 is left to Condition 1 alone to supply. We have the opportunity to find u = 16 through all three conditions for n = ±33, but a(68) = 16. Similarly, we might have instigated u = 35 via Condition 1 for n = ±80, but a(1842) = 35. The least-missing u = 38 is particularly “sticky”; once it appears at a(5609), many larger m have already filled in. The same can be said for u = 181, appearing at a(224404), supplanted by u = 864.
Therefore there are three “regions” as regards least-unused u. Region I has a is completely covered and u is larger than the record. Region II offers more than one condition to furnish u. Finally, region III offers only Condition 1 to furnish u. The boundary between region I and II is n = 15. The boundary between II and III is n = ±80.
Conjecture: a eventually sees all m ≥ 0 as n → ∞. If this is true, it is clear that n may prove large in order to see even relatively small missing m. This is tantamount to saying that eventually, all m are reiterated in a, essentially for the least-missing m, via Condition 1, i.e., the difference (n − k).
Maxima and minima.
The (absolute) minimum in a is a(1) = 0, whereas 1 appears at local minima with the following indices:
2, 4, 7, 12, 22, 36, 154, 258, 26612, 32257, 113736, 187906, ...
The occasion of m = 1, aside from the cases a(2) = (n − c) and a(4) = c, represents adjacent appearances of m in a. The numbers m repeated, respectively, are:
2, 5, 11, 17, 40, 64, 17, 60, 13, 75, ...
There doesn’t seem to be a prohibition against restated terms, therefore m = 1 may occur infinitely as n → ∞, however sparsely.
The maxima include 0 (given), 1 and 2 (instigated by novel nonprimes), a(8) = 3 (instigated by Condition 1), and only 3 instigated by novel primes, 3 → a(9) = 4, 7 → a(17) = 9, and 13 → a(29) = 15. For n > 29, novel primes do not instigate records, since n – c > c for all n > 38. There are very many records compared to local minima.
There are roughly 2 regions as regards the counting function c. Region I concerns the number of primes in a greater than the number of nonprimes. For n > 38, the number of nonprimes exceeds the number of primes in a, with the counting functions generally divergent, hence the balance of the sequence lies in Region II.
Runs of records.
Records may occur in runs for 260 ≤ n ≤ 1953. There are 32 runs with lengths ℓ ≤ 12. The first run 1 ≤ n ≤ 3 is trivial and includes 0…2. The second run 9 ≤ n ≤ 10 is instigated by 3 and includes 4 and 5. The third run 28 ≤ n ≤ 29 is instigated by a novel nonprime 12 and includes 13 and 15.
All other runs are instigated by novel nonprimes and contain a run of consecutive m.
Table 2 lists the record-runs in a. The first column lists the indices of the run, followed by the run length ℓ, the instigator m and the entry condition code b1, the exit condition code b2, and the values a(n) in the final column. If the values constitute a run, these are listed with the first and last values separated by ellipsis, and in the case of non-consecutive values, by a braced list.
n ℓ m b_1 b_2 a(n)
--------------------------------------------------
1...3 3 - - 1 0...2
9...10 2 3 0 1 4...5
28...29 2 12 -1 -1 {13, 15}
265...274 10 180 -1 1 182...191
316...317 2 221 -1 -1 222...223
320...322 3 224 -1 -1 225...227
328...330 3 230 -1 0 231...233
334...338 5 234 -1 1 235...239
343...351 9 242 -1 1 243...251
355...358 4 253 -1 1 254...257
364...366 3 260 -1 0 261...263
374...375 2 267 -1 1 268...269
382...385 4 273 -1 -1 274...277
388...390 3 278 -1 1 279...281
602...608 7 450 -1 1 451...457
656...660 5 494 -1 1 495...499
664...665 2 501 -1 1 502...503
670...672 3 506 -1 1 507...509
702...713 12 529 -1 1 530...541
717...720 4 543 -1 1 544...547
729...732 4 553 -1 -1 554...557
735...739 5 558 -1 1 559...563
758...759 2 575 -1 1 576...577
919...921 3 706 -1 -1 707...709
924...932 9 710 -1 1 711...719
1023...1024 2 795 -1 1 796...797
1028...1038 11 798 -1 1 799...809
1645...1655 11 1308 -1 1 1309...1319
1903...1909 7 1524 -1 1 1525...1531
1913...1922 10 1533 -1 1 1534...1543
1941...1943 3 1556 -1 1 1557...1559
1949...1953 5 1562 -1 1 1563...1567
These record-runs appear to be instances where Condition 1 fails to produce differences (n − k) > (n − c), or, rather, we have the condition c < k. The runs are broken when either we have a novel m or we hit an extant m. That is, we burn through a series of novel composite m. Hence, the runs begin with a record-setting novel nonprime m = (n − c) thereafter, (n − c) is also a novel nonprime m.
There are 3 regions in a as regards record-runs. Region I includes the trivial runs that either involves records or a discontinuous set of m. Region II includes all the runs that have runs of m, i.e., a(n) for 265 ≤ n ≤ 1953. Region III includes a(n) for n ≥ 1954.
Figure 1 is a scatterplot of a(n) for 1 ≤ n ≤ 4096 appears below. (Click for an enlarged plot for 1 ≤ n ≤ 218.)
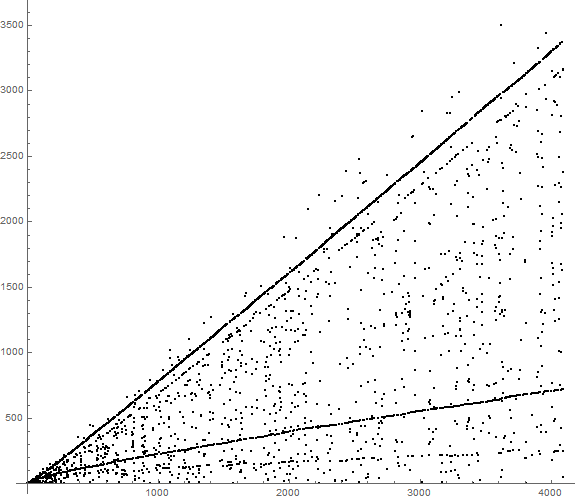
Figure 2 is a scatterplot of a(n) for 1 ≤ n ≤ 256, color coded to show labeled records in red, local minima (a(1) = 0 and any instance of m = 1) in blue, terms attributable to Condition −1 (a novel nonprime progenitor) in green, and those attributable to Condition 0 (a novel prime progenitor) in gold. All other terms m appear in black. The light blue horizontal line represents the least-unused u, below which, all m instigate Condition 1.
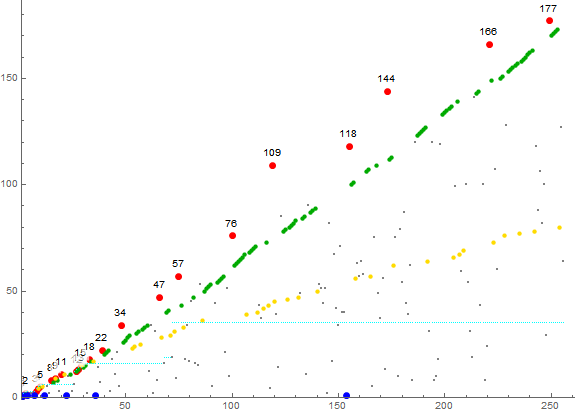
We employ the NATO alphabet so as to obtain names for features of the graph and to avoid Greek letters as these conflict with designations for common number theoretical functions. We also want to avoid strict association with, for example, novel primes, etc., since the features do not necessarily attribute fully with these entities.
Proceeding clockwise from the y-axis to the x-axis, we identify basic features evident in the scatterplot of Figure 2.
The records are labeled and appear in red.
The “november” stream derives from Condition −1, that is, for novel nonprime a(n), shown in green.
The “papa” stream derives from Condition 0, that is, for novel prime a(n), shown in gold.
The light blue horizontal line is the plot of the step-function u(n), that is, the smallest m that does not appear in a.
The local minima appear in blue and include 0 ≤ m ≤ 1.
Figure 3 is a scatterplot of a(n) for 1 ≤ n ≤ 214, color coded as in Figure 3, but adding orange to signify m for which a(n−2) is a novel prime, and purple, m for which a(n−3) is a novel prime.
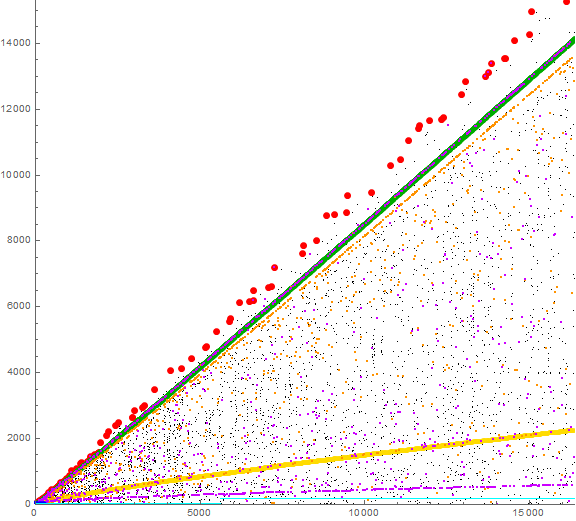
In addition to these primary features, we see the further streams “quebec”, the first “echo” of papa, and November, “romeo”, the secondary echo near the bottom of the graph. Not all of the terms instigated by m in the golden striation end up in these echoes.
As n increases, new echoes appear within these two (sierra and tango — see the enlarged plot). A clear rationale for sierra and tango have not been identified, but these are probably further echoes. We must recall that quebec and romeo are not sure-fire effects of novel primes. Additionally, the general vertical chatter seems to be a feedback effect as well.
We can see in the large-scale plot a pair of ghostly rays of negative space, yankee and zulu, seen in large-scale scatterplots of a(n). These two rays appear approximately centered upon a line of slope 15/32.
Further, we see that the plot appears denser below november, and that a fringe area between november and the records we call “hotel” contain rarified terms. These appear to be outside the reverberations generated by Condition 0, a matter to be investigated.
We now investigate a transformation of a.
Let s(n) = a(n) + a(n+1) + 1. The sequence begins:
2, 4, 4, 4, 5, 4, 5, 8, 10, 11, 7, 7, 8, 11, 16, 17, 18, 12, 15, 23, 13, 12, 22, 15, 10, 19, 26, 29, 30, 30, 18, 21, 36, 35, 19, 16, 22, 30, 43, 42, 44, 26, 22, 30, 33, 27, 40, 61, 54, 56, 58, 53, 48, 55, 62, 57, 58, 66, 68, 47, ...
Figure 4 is a scatterplot of s(n) for 1 ≤ n ≤ 216 (see an enlarged plot for 1 ≤ n ≤ 218.)
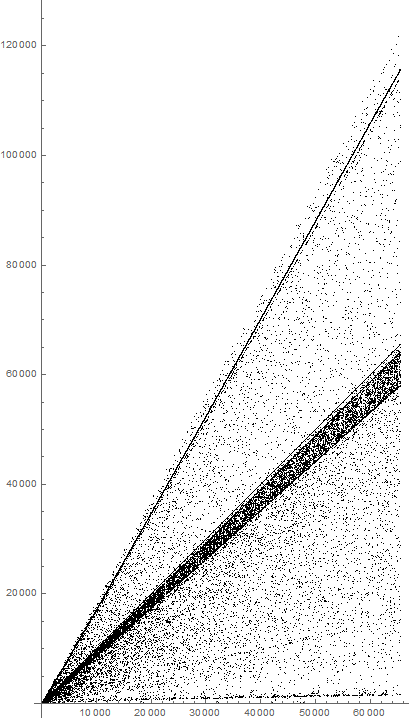
We can identify some prominent structures in this plot.
Since we are examining adjacent pairs of terms a(n) and a(n+1) and since we have three conditions {−1, 0, +1}, we have 9 possible associations for the terms in s. We may convert the conditions into a ternary number and obtain a decimal equivalent so as to trace the provenance of a given term in s, however here we will abbreviate the conditions as 0 = NN, 1 = NP, 2 = NX, etc., according to Table 3, with the novel nonprime condition −1 rendered as N, the novel prime condition 0 as P, and the extant condition +1 as X. The numbers admit algorithmic color-coding to Figure 5.
We store the abbreviated conditions in an auxiliary sequence t(n).
Table 3.
| t(n) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| a(n) | N | N | N | P | P | P | X | X | X |
| a(n+1) | N | P | X | N | P | X | N | P | X |
| Color | • | • | • | • | • | • | • | • | • |
Hence, the condition pair PX pertains to a(n) from novel prime, and a(n+1) extant.
Figure 5 is a scatterplot of s(n) for 1 ≤ n ≤ 28 employing the color function in Table 3.
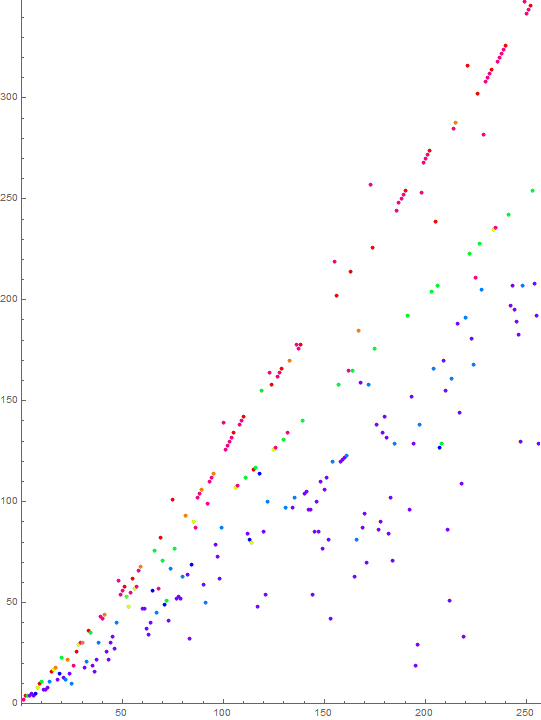
Figure 5 suggests that generally, novel nonprime a(n) instigates s(n) ≥ n, and novel prime a(n) instigates s(n) = n. Extant a(n) instigates s(n) < n.
Figure 6 is a scatterplot of s(n) for 1 ≤ n ≤ 214 employing the color function in Table 3.
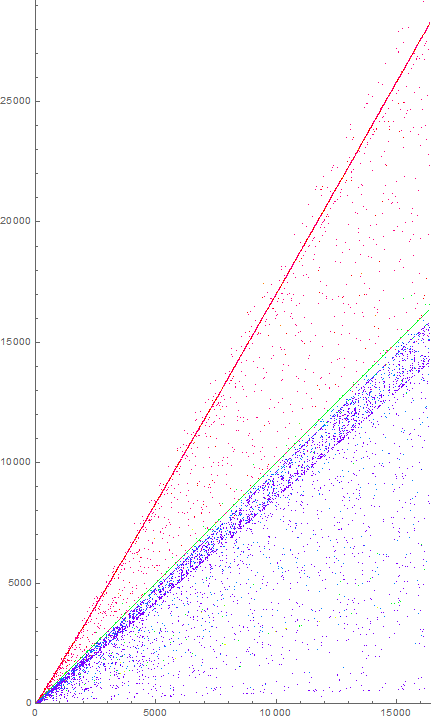
There are features in the plot of s similar to that of a.
We find the following regarding striations and bands in the plot of s:
Alfa: the upper prominent striation primarily associates with t(n) = 0 (NN • magenta) and is an up-turning curve beginning roughly slope 3/2 but moving toward and not necessarily bounded by 5/3.
Bravo: the second ray associates with t(n) = {3, 4, 5}, (PN • chartreuse, PP • green, PX • viridian) that is, one or both pair of numbers a(n) and a(n+1) involve a novel prime. It has slope near 1 and is apparently bound by n.
Charlie: the upper bound of the band has an up-turning curve that hovers around and crosses slope 15/16. This feature is primarily associated with t(n) = {6, 7, 8}, (XN • blue, XP • indigo, XX • violet) that is, one or both pair of numbers a(n) and a(n+1) involve an extant m.
Delta: the lower bound of the band has an up-turning curve that hovers around and crosses slope 5/6. This feature shares the associations of charlie.
The reinforced edge of the band at Charlie and Delta primarily associate with pairs of old numbers (XX • violet). These old pairs seem to be constrained below slope 1.
Pairs of novel nonprimes (NN • magenta) are primarily above slope one with notable exceptions greater than slope 5/6 (Delta).
It is likely that Charlie and Delta are echoes of the prime and nonprime rays Bravo and Alfa, respectively.
This concludes our examination.
Appendix:
Block[{a = {0}, c = 0},
Monitor[Do[If[FreeQ[Most@ a, a[[-1]] ],
If[PrimeQ[a[[-1]] ], c++; AppendTo[a, c], AppendTo[a, i - c]],
If[PrimeQ[a[[-1]] ], c++]; AppendTo[a,
FirstPosition[Reverse@ Most@ a, a[[-1]] ][[1]] ] ], {i, 2^16}], i]; a] ]
Document Revision Record.
2021 0301 2100 Draft 1.