The Flight and Demise of Icarus.
A sequence of David Sycamore.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0304.
Abstract.
We examine a nested doubly conditional self-referential sequence with contramanding counting functions that produces two major canonical nontrivial trajectories and 76 departures from such. We study the effect of the initial term x, considered a seed, as well as explore the tree of possible trajectories.
Introduction.
This paper describes a doubly conditional self-referential recursive mapping h(x), where x ≥ 0 is an integer used as a seed. The recursive mapping of h(x) produces an infinite sequence, however, there is a mechanism that eventually arises given any x that results in a fixed point of 0.
The map h(x) produces a sequence beginning with sx(0) = x, incrementing thereafter n times. We subject the term x to Condition A, a novelty test, and in both outcomes, to Condition B, a primality test, yielding output based on the four possible overlaid conditions. The output serves as input for another mapping until we encounter two adjacent zeros (a fixed point of 0). We say a number m is novel if it does not already appear in s, and extant if it already appears at least once at s(k) for k < n.
Therefore, we define a sequence sx starting with sx(0) = x.
For novel prime s(n), we report the number c of primes m in s at s(n+1).
For novel nonprime s(n), we report the number (n − c) of nonprimes m in s at s(n+1).
For extant prime s(n) whose penultimate index is k, we write at s(n+1) the number of nonprimes in s(j), k < j < n.
For extant nonprime s(n) whose penultimate index is k, we write at s(n+1) the number of primes in s(j), k < j < n.
Conditional structure of s.
There are 4 practical conditions, to which we assign labels.
- Condition 0 pertains to novel nonprimes m wherein we do not increment c, and enter s(n+1) = (n − c).
- Condition 1 pertains to novel primes m wherein we increment c and enter s(n+1) = c.
- Condition 2 pertains to extant nonprimes m seen at s(k), k < j < n, wherein we do not increment c but report the number of prime s(j).
- Condition 3 pertains to extant primes m seen at s(k), k < j < n, wherein we increment c and report the number of nonprime s(j).
We use these conditions to produce an auxiliary sequence r that tracks the condition enacted during each iteration.
The general effect of Conditions 0 and 1 (the novel conditions) is to introduce the status of c or (n − c) at s(n+1) if and only if m is novel. Since there are more nonprimes than primes in the intervals dealt with during generation, the trajectory of (n − c) proves higher and more continuous than that of c in the scatterplot of s. Each time Condition 0 or 1 occurs, the respective counting function has strictly increased. Therefore, generally, the emergence of these conditions has a sustaining effect upon the duration of a nontrivial run of s. Using the analogy of Icarus, these two conditions perhaps represent his flight, maybe a bit too close to the sun.
The general effect of Conditions 2 and 3 (the extant conditions) is to report the number of integers in the interval between the latest 2 instances of m with opposite primality at s(n+1). Hence, Condition 3 (pertaining to extant primes) tends to report larger numbers of nonprimes more infrequently than Condition 2 reports smaller numbers of primes. Condition 2 tends to be the reason that forces s into a fixed point through instigating 2 adjacent zeros. Again, the analogy of Icarus has us consider these conditions as Icarus’ fateful accumulation of sea-spray until he crashes into the Aegean.
Generation of sequence s.
We now examine three examples of the recursive mappings of h(x) given seeds 1, 2, and 12.
s1 begins:
1, 1, 0, 3, 1, 1, 0, 1, 0, 0, ...
s1(1) = 1 since s1(0) is a novel nonprime, and there is 1 nonprime in the sequence.
s1(2) = 0 since s1(1) is a nonprime that appeared at s1(0); between s1(0) and s1(1) there are no primes.
s1(3) = 3 since s1(2) is a novel nonprime, and there are 3 nonprimes in the sequence.
s1(4) = 1 since s1(3) is a novel prime, and there is 1 prime in the sequence.
s1(5) = 1 since s1(4) is a nonprime that appeared at s1(1); between s1(1) and s1(4) there is 1 prime.
s1(6) = 0 since s1(5) is a nonprime that appeared at s1(4); between s1(4) and s1(5) there are no primes.
s1(7) = 1 since s1(6) is a nonprime that appeared at s1(2); between s1(2) and s1(6) there is 1 prime.
s1(8) = 0 since s1(7) is a nonprime that appeared at s1(5); between s1(5) and s1(7) there are no primes.
s1(9) = 0 since s1(8) is a nonprime that appeared at s1(6); between s1(6) and s1(8) there are no primes.
For n > 9, we will always have 0 since there are no primes between adjacent zeros, and the sequence is hereinafter trivial. Hence, we may speak of a nontrivial run length ℓ, the number of iterations necessary to produce 2 adjacent zeros. Therefore, ℓ1 = 8.
s2 begins:
2, 1, 1, 0, 3, 2, 3, 0, 3, 1, 4, 6, 7, 6, 1, 1, 0, 2, 8, 12, 13, 8, 1, 2, 4, 4, 0, 3, 14, 19, 11, 12, 5, 13, 7, 13, 0, 7, 1, 9, 23, 18, 24, 25, 26, 27, 28, 29, 19, 10, 30, 31, 21, 32, 33, 34, 35, 36, 37, 22, 38, 39, 40, 41, 23, 18, 6, 18, 0, 8, 16, 47, 25, 7, 27, 8, 2, 35, 6, 3, 34, 7, 5, 33, 9, 13, 35, 4, 22, 9, 1, 14, 21, 10, 11, 44, 64, 65, 66, 67, 33, 3, 16, 10, 3, 2, 20, 71, 37, 34, 10, 4, 7, 21, 8, 13, 21, 1, 9, 9, 0, 16, 6, 13, 7, 9, 2, 14, 12, 31, 55, 87, 88, 89, 45, 90, 91, 92, 93, 94, 95, 96, 97, 46, 98, 99, 100, 101, 47, 54, 102, 103, 49, 104, 105, 106, 107, 50, 108, 109, 51, 110, 111, 112, 113, 52, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 53, 54, 6, 14, 11, 67, 63, 131, 57, 132, 133, 134, 135, 136, 137, 58, 138, 139, 59, 60, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 61, 62, 150, 151, 63, 7, 69, 153, 154, 155, 156, 157, 65, 33, 32, 44, 33, 0, 25, 40, 43, 66, 34, 28, 48, 169, 170, 171, 172, 173, 67, 43, 8, 30, 49, 20, 33, 4, 31, 93, 25, 5, 128, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 72, 192, 193, 73, 74, 194, 195, 196, 197, 75, 198, 199, 76, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 77, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 78, 224, 225, 226, 227, 79, 80, 228, 229, 81, 230, 231, 232, 233, 82, 234, 235, 236, 237, 238, 239, 83, 84, 240, 241, 85, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 86, 252, 253, 254, 255, 256, 257, 87, 43, 85, 3, 189, 18, 65, 24, 71, 192, 18, 1, 50, 40, 25, 20, 21, 50, 0, 25, 0, 0, ...
Run length ℓ2 = 364. This pattern pertains to an infinite number of primes and has many defects.
s12 begins:
12, 1, 2, 1, 1, 0, 5, 2, 3, 4, 6, 7, 5, 2, 2, 0, 7, 1, 8, 10, 11, 10, 1, 1, 0, 2, 8, 2, 1, 2, 1, 1, 0, 3, 15, 21, 22, 23, 15, 1, 2, 8, 5, 19, 18, 27, 28, 29, 19, 3, 9, 30, 31, 22, 8, 6, 18, 4, 18, 0, 9, 1, 7, 32, 41, 24, 42, 43, 25, 44, 45, 46, 47, 26, 48, 49, 50, 51, 52, 53, 27, 9, 5, 29, 26, 3, 27, 3, 1, 9, 4, 9, 0, 9, 0, 0, ...
Run length ℓ12 = 94. This pattern pertains to an infinite number of nonprimes and has many defects.
We see that there are three principal conditions of such sequences s, based upon the nature of the seed. Since s(1) = 1 for any input, the seed x = 1 begins {1, 1, 0, …}, the 0 arising from two adjacent nonprimes. Given a prime seed x = P, we have {P, 1, 1, …}, and a nonprime seed x = N, we have {N, 1, 2, …}.
Defects arise in the latter two P and N trajectories when x conflicts with the same x that arises later in the trajectory. The conflict involves converting a novel to an extant progenitor s(n), normally resulting in a vastly different report at s(n+1). A key consideration is that the novelty test when positive requires reporting the number c or (n − c), with c incrementing upon the occasion of both novel and extant primes, granting opportunities for gaps in the reporting of the counting functions c or (n − c) through which certain seeds x pass, so as not to disturb the canonical sequence.
Canonical Trajectories.
There are 3 “canonical trajectories” that derive from the 4 possible conditional states that govern the sequence s. These include the novel nonprime (NN) and the novel prime (NP) canonical trajectories pertaining to conditions 0 and 1, respectively. There is also an “extant” trajectory (X) that is determined by s1(1) = 1. Of course, the trajectory of x = 1 is not truly an extant one, since by definition the seed is introduced and thus novel. However, the extant condition comes into play at s1(2) = 0. We might also see x = 1 simply as a novel nonprime variant that departs at n = 2.
For all x, we have s(1) = 1, since s(0) = x is novel. Regardless of primality, for n = 1, there is 1 instance of the appropriate species (nonprime or prime) in s. If x is prime, then s(2) = 1 else s(2) = 2 except in the case of x = 1.
The Canonical Extant Trajectory.
We have already shown that, for x = 1, s1(2) = 0, since 1 has already appeared at s1(0). Therefore we report the number of primes between s0 and s1, which of course is 0.
Let’s use a sequence condition diagram that colors the term according to the conditional state imparted by s(n−1). Red indicates a novel prime progenitor, yellow a novel nonprime. Blue indicates an extant prime progenitor and green an extant nonprime. Further, we note the index n above s(n). We ignore the trivial infinite coda of zeros that follow the last nonzero term.
Figure S1:
![]()
Therefore, we see that we never have a “blue” or extant prime arise in the trajectory, and we mark the departure of the novel trajectories from this canonical extant trajectory at n = 2 with a black circle and a red dot under it.
Note there are 3 possible values for s(2); for x = 1, s1(2) = 0, for x prime we have sP(2) = 1, and for x ≠ 1 and nonprime, we have sN(2) = 2.
The Canonical Nonprime Trajectory.
Let us consider a seed x ≠ 1 and suppose it is a nonprime N that does not interfere with any element in the trajectory. Therefore, we derive a pattern sN as follows:
Figure S12:
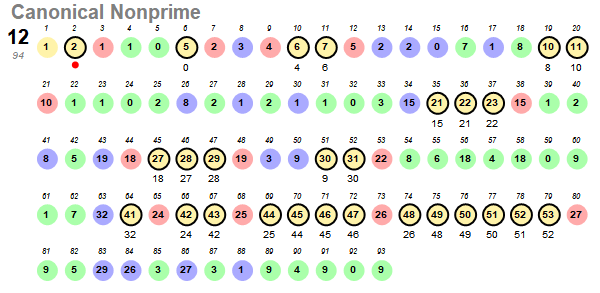
This trajectory has length ℓN = 94 and first arises for N = 12. We find that if ever N does appear in sN , it induces a departure from this canonical nonprime trajectory. This is because, for x = N, N already appeared at k = 0, therefore its appearance at n is its second appearance, meaning it is now an extant nonprime and triggering Condition 2 instead of Condition 0. It could be possible to end up with the canonical sequence anyway. For that to happen, Condition 2 would yield the same s(n) as Condition 0. There are only 26 conflicting nonprime seeds and all have been observed to deviate from the canonical nonprime trajectory.
Figure P12 is an annotated scatterplot of sN = s12 using the same color function:
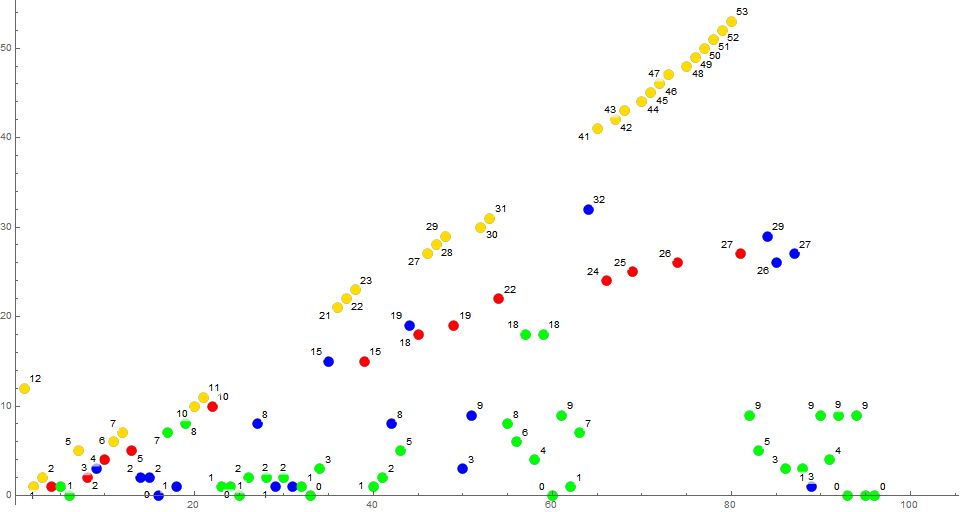
It is interesting to note the airborne yellow path related with the reporting of the number (n − c) of nonprimes in s, and the similar sparser number c of primes in s in red. Again, these counting functions escalate even though they are not reported in the extant Conditions 2 and 3. We also see generally elevated numbers of nonprimes between the last 2 instances of primes in blue, as compared to the denser and smaller numbers of primes between the last 2 instances of nonprimes in green. The plot shows the first 2 trivial zeros.
The death knell appears to be the instance of two adjacent extant numbers of the same primality status, followed by 0, then a third term of same primality status.
The Canonical Prime Trajectory.
Let us consider a prime seed x, supposing it is a prime P that does not interfere with any element in the trajectory. We produce a pattern sP as follows:
Figure S2:
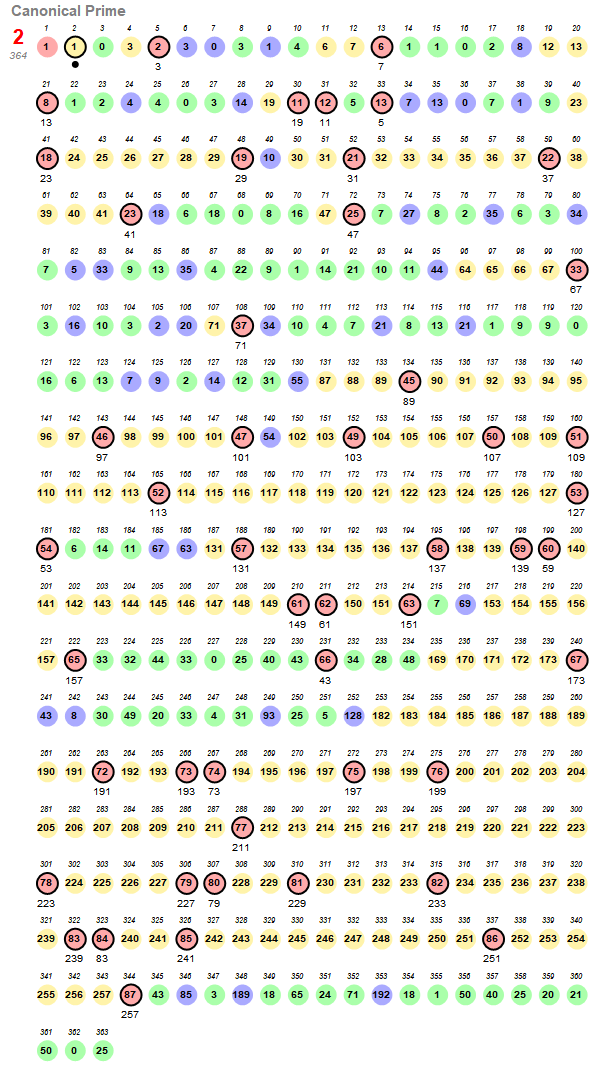
This trajectory has length ℓP = 364 and first arises for P = 2 (since it is the least prime). We find that if ever P does appear in sN , it induces a departure from this canonical prime trajectory. This is because, for x = P, P already appeared at k = 0, therefore its appearance at n is its second appearance, meaning it is now an extant prime and triggering Condition 3 instead of Condition 1. It could be possible to end up with the canonical sequence anyway. For that to happen, Condition 3 would yield the same s(n) as Condition 1. There are only 49 conflicting prime seeds and all have been observed to deviate from the canonical prime trajectory.
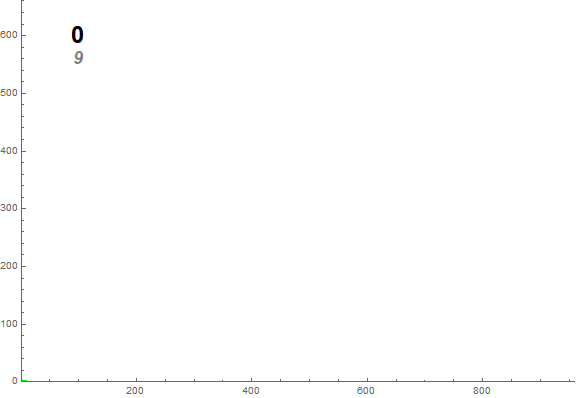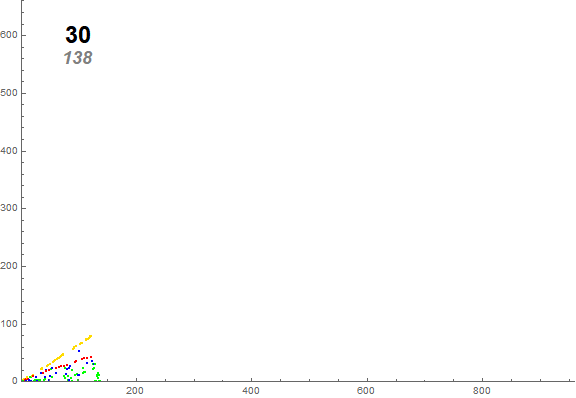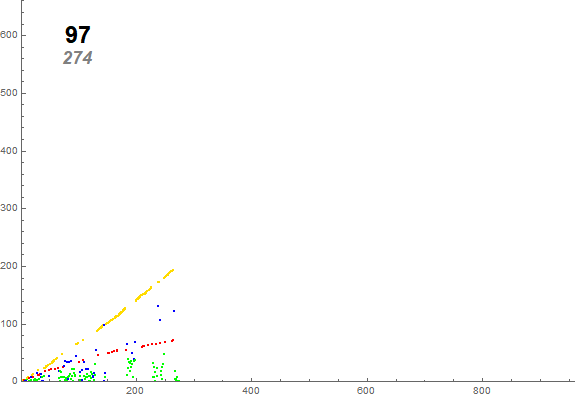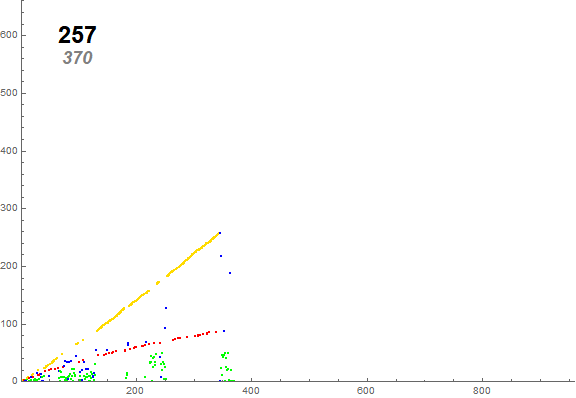
Figure P2 is a scatterplot of s2:
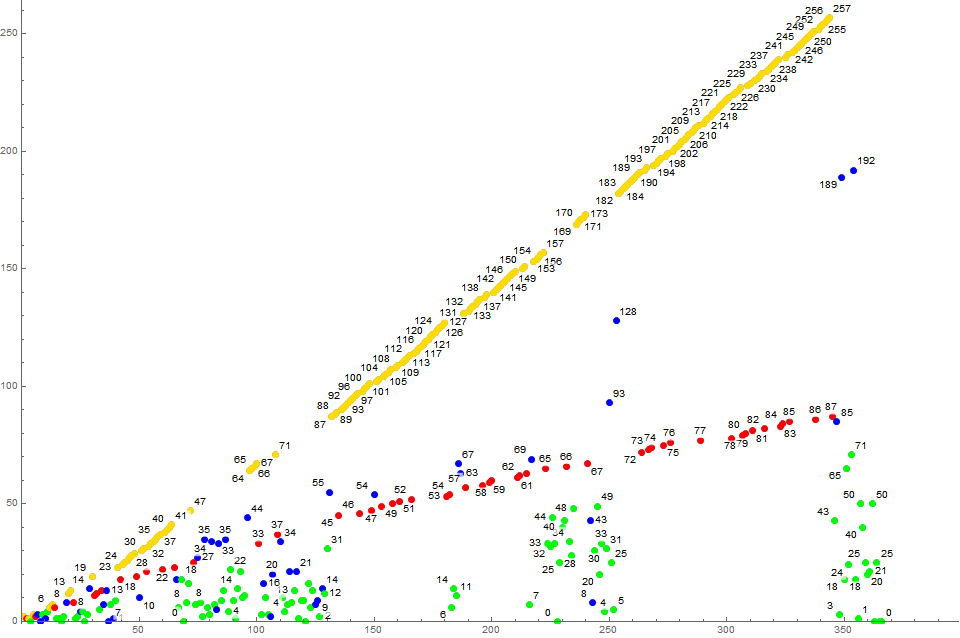
Transmissivity of the Canonical Trajectories.
Let us examine the canonical trajectories to determine the gaps in coverage that serve as “holes” in the multiset through which seeds x may pass without disturbing any element in the trajectory.
The canonical extant trajectory pertains precisely to x = 1 since s(1) = 1 for all x. There are no defects from this trajectory. We may consider s2 to be a defect from the canonical novel trajectories s2 and s12.
For the canonical prime trajectory s2, we have ℓ2 = 364 with the maximum s2(343) = 257 and last term 25. Taking the complement of (1…257) and s2, the following numbers are not in s2:
15, 17, 42, 56, 68, 70, 129, 130, 152, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 174, 175, 176, 177, 178, 179, 180, 181.
The only primes that pass through s2 are {17, 163, 167, 179, 181}: these and all primes p > s2(343) share the trajectory s2. All the primes that interfere with the trajectory s2 present their own distinct trajectory that departs from that of s2. These 49 defects are listed below:
3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 173, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257.
These primes p appear in the following order in s2:
(2), 3, 7, 13, 19, 11, 5, 23, 29, 31, 37, 41, 47, 67, 71, 89, 97, 101, 103, 107, 109, 113, 127, 53, 131, 137, 139, 59, 149, 61, 151, 157, 43, 173, 191, 193, 73, 197, 199, 211, 223, 227, 79, 229, 233, 239, 83, 241, 251, 257.
We see that the departure of sp from s2 occurs progressively later as to the above ordering. The concordance of sp and s2 has length k + 1, where s2(k) = p is the first appearance of p in s2. There are no departures from any sp, hence the departures on account of prime seed p occur if p appears in s2 and the conflict occurs at the first appearance s2(k) = p.
The canonical nonprime trajectory s12, we have ℓ12 = 93 with the maximum s2(79) = 53 and last term 9. Taking the complement of (1…53) and s12, the following numbers are not in s12:
12, 13, 14, 16, 17, 20, 33, 34, 35, 36, 37, 38, 39, 40
Of these, {12, 14, 16, 20, 33, 34, 35, 36, 38, 39, 40, 54} are not in s12. These and all nonprimes m > s12(79) share the trajectory s12. Therefore, we have the following 26 conflicting nonprime seeds:
0, 4, 6, 8, 9, 10, 15, 18, 21, 22, 24, 25, 26, 27, 28, 30, 32, 42, 44, 45, 46, 48, 49, 50, 51, 52
These nonprimes m appear in the order in s12 presented below:
0, 4, 6, 8, 10, 15, 21, 22, 18, 27, 28, 9, 30, 32, 24, 42, 25, 44, 45, 46, 26, 48, 49, 50, 51, 52
We see that the departure of sm from s12 occurs progressively later as to the above ordering. The concordance of sm and s12 has length k + 1, where s12(k) = m is the first appearance of m in s12. There are no departures from any sm, hence the departures on account of nonprime seed m occur if m appears in s12 and the conflict occurs at the first appearance s12(k) = m.
It is clear that all seeds x > s2(343) = 257 do not conflict with any canonical term m, hence nonprimes share trajectory s12 and primes share trajectory s2. We see that 49 prime defects + 26 nonprime defects = 75, and we add the 3 canonical trajectories to arrive at the 78 possible trajectories of Icarus’ ever-fateful flight.
Icarus’ lamest flight starts with seed x = 0:
Figure S0:
![]()
In Figure S0 we ghosted out the terms that also appear in sN, with the collision at n = 5 in red figures. The first term that differs from sN is s0(6) = 1. This proves to be a faster fateful error! The flight has length ℓ0 = 7.
Icarus’ most glorious and longest-lasting flight starts with the prime seed x = 43:
Figure S43 ignores the terms that agree with sP for brevity:
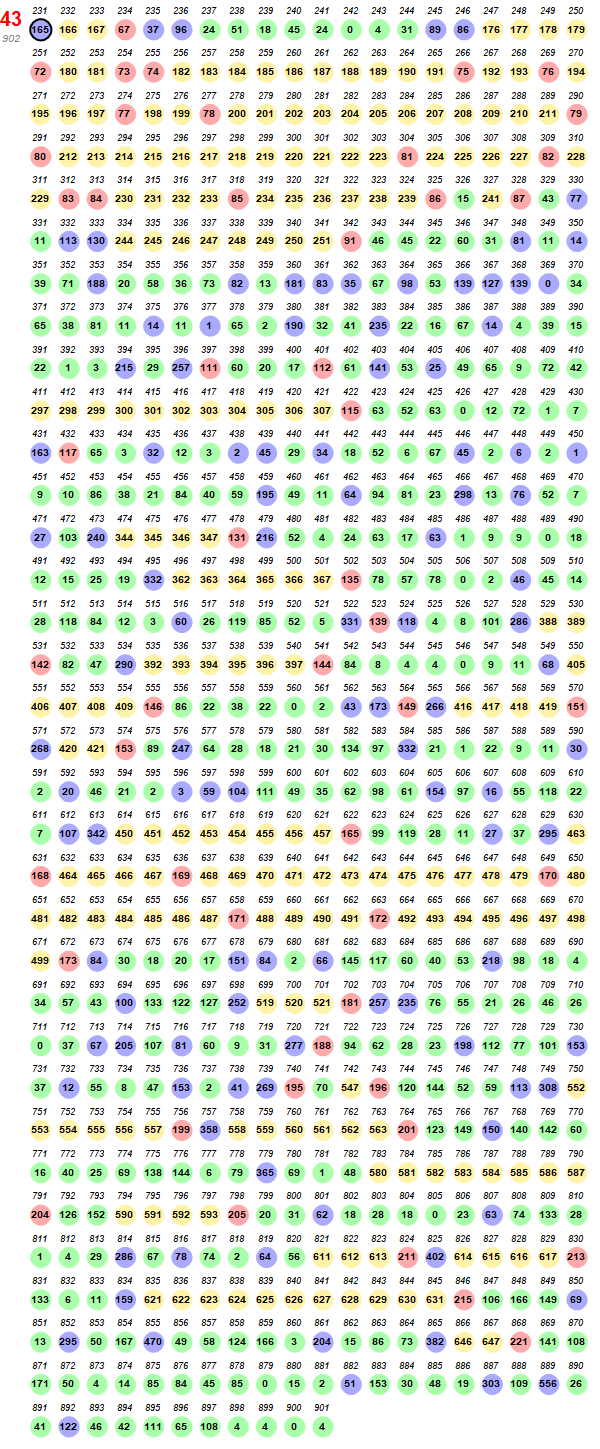
Figure S43 describes a sustained flight that lasts nearly 3 times as long at ℓ43 = 902 as ℓP = 364.
Figure P43 is a scatterplot of s43:
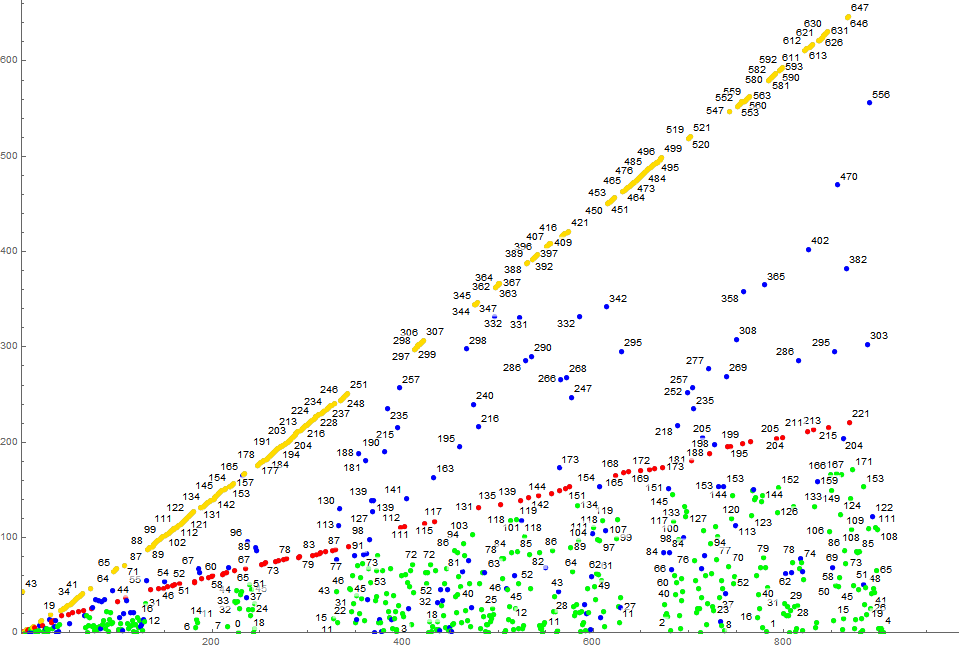
The longest nonprime flight pertains to x = 21 with ℓ21 = 505.
Figure 2 is an animation of scatterplots of all 78 trajectories.
The Effect of Defection from Canon.
The canonical trajectories are those that allow the sequence sP or sN to progress unimpeded by collision with a prime seed x = p or a nonprime seed x = N. The collisions affect the first appearance of x in the canonical trajectory s, transmuting its conditional mode from a novel to an extant prime or nonprime.
The transmutation of a novel nonprime to an extant nonprime necessitates the application of Condition 2 (green) in place of Condition 0 (yellow). Therefore, instead of reporting the number (n − c) of nonprimes in s, we report the number qp of primes between s(k) and s(n). The number (n − c) increases quite rapidly and more often, whereas qp tends to be a “random” yet relatively small number. The later the interaction of seed x with its appearance in the canonical nonprime trajectory, the greater the tendency to “kill” the flight of Icarus.
The transmutation of a novel prime to an extant prime necessitates the application of Condition 3 (blue) in place of Condition 1 (red). Therefore, instead of reporting the number c of primes in s, we report the number qn of nonprimes between s(k) and s(n). The number c increases mildly, whereas qn tends to be a “random” and widely scattered number.
As regards the nonprime collisions, 13 result in a shortened run length and 12 prolonged, with 1 (that of x = 15) the same length ℓ12 = 93. The mean reduction is −31.15 terms, while the mean lengthening is +79 1/3 terms. Collisions that occur near the middle of the canonical run length ℓ12 are more likely to outlast ℓ12. Those that happen after 72 iterations tend to reduce run length.
Regarding the prime collisions, 31 are reduced and 18 are lengthened from ℓ2 = 364 terms. The mean reduction is −155.097 terms, while the mean lengthening is +93.44 terms. The collisions that transpire later in the canonical run length ℓ2 tend to outlast ℓ2. The seeds x that have a concordance with canon less than 160 terms all suffer shortened lives.
There doesn’t appear to be a pattern among the defective seeds that would either predictably prolong or reduce the flight of Icarus.
The Tree of Icarus’ Trajectories.
We can plot a tree of all the possible trajectories s by bringing together the sequence condition diagrams for all 78 distinct seeds x, rendered in a linear fashion. For the canonical trajectories, we show all terms. For the seeds x that depart from these, we need only show the terms that depart from these canonical trajectories.
Figure 1 is a tree proceeding from left to right that shows the canonical tranjectories in the middle, with nonprimes on top, 1 in the middle, and primes on the bottom, arranged in order of the appearance of defective x in canonical trajectory so as to avoid crossing leaderlines to the term of departure s(k+1). (View an enlarged abbreviated table showing conditional states and trajectory identities and lengths in italic after the nontrivial chain. View a fully annotated chart showing all 78 sequences.)

As captive of King Minos, Daedalus perhaps hadn’t considered that Icarus can’t possibly win regardless of the seed he used. Maybe he gamed it out there in the lofty cool of his cell, only after the boy took flight—all the possible trajectories Icarus could take, only to break down knowing escape wouldn’t prove possible. The question remains, could we find a seed that would allow the boy to fly away as planned? If we apply negative x, since no negative m appear in s, we would see no conflict and get the canonical nonprime trajectory (unless one construes a negative prime as a prime, as some CAS packages do). We might apply a series of initial terms, perhaps, and find an infinite and nontrivial sequence. In any case, we are fighting the propensity of the extant conditions to pull Icarus down from the novel flight path and into the sea.
Appendix:
Table A: Aggregate data for each trajectory.
Column “x” pertains to seed x; “PM” to the primality of x: x denotes the empty product, p denotes prime, n nonprime.
Column “ℓ” is the nontrivial run length of sx, while D is the index of departure from the primality-canon.
The
“Modes” section counts the conditions that appear in sx. c0 pertains to novel nonprimes, c1 to novel primes, c2 to extant nonprimes, and c3 to extant primes.
The
“Maximum” section pertains to the largest term in sx, listing the maximum, its index, and the instigating condition.
The
“Last” section regards the last nontrivial term in sx, listing the term and the instigating condition.
| Modes | Maximum | Last
| NN NP XN XP | |
x PM ℓ D c0 c1 c2 c3 max position c last c
--------------------------------------------------------------------------
1 x 7 [X] 2 1 4 0 3 3 0 1 2
--------------------------------------------------------------------------
2 p 363 (P) 180 50 93 40 257 343 0 25 2
3 p 153 4 55 23 50 25 97 144 0 14 2
5 p 126 32 35 16 51 24 59 89 0 4 2
7 p 98 12 39 17 26 16 61 93 0 9 2
11 p 34 30 7 6 14 7 19 {29, 31} 3 4 2
13 p 45 20 12 8 17 8 23 38 0 1 2
19 p 207 29 78 28 71 30 127 179 0 12 2
23 p 97 40 27 14 35 21 47 73 0 1 2
29 p 58 47 14 9 23 12 29 {47, 48} 3 1 2
31 p 114 51 36 15 40 23 71 107 0 8 2
37 p 84 58 25 13 29 17 47 76 0 4 2
41 p 95 63 30 13 34 18 47 71 0 4 2
43 p 901 230 307 83 369 142 647 867 0 4 2
47 p 295 71 123 40 91 41 197 275 0 1 2
53 p 406 180 202 54 106 44 293 388 0 33 2
59 p 202 198 82 28 59 33 139 {197, 199} 3 21 2
61 p 462 210 184 56 152 70 317 439 0 35 2
67 p 127 99 32 16 54 25 71 107 0 1 2
71 p 298 107 114 38 103 43 211 291 0 15 2
73 p 347 266 161 47 94 45 251 337 0 16 2
79 p 403 306 173 48 121 61 257 347 0 40 2
83 p 329 322 162 47 82 38 239 {321, 323} 3 20 2
89 p 137 133 35 16 56 30 89 {133, 134} 3 6 2
97 p 271 142 112 34 87 38 193 263 0 8 2
101 p 153 147 47 18 58 30 101 {147, 148} 3 8 2
103 p 324 151 149 43 87 45 223 308 0 35 2
107 p 351 156 172 49 88 42 251 341 0 38 2
109 p 166 159 55 21 59 31 109 {159, 160} 3 9 2
113 p 672 164 270 77 240 85 487 646 0 8 2
127 p 497 179 204 56 163 74 349 473 0 4 2
131 p 422 187 188 49 130 55 307 409 0 9 2
137 p 398 194 153 47 139 59 277 379 0 1 2
139 p 392 197 164 53 123 52 281 385 0 32 2
149 p 373 209 153 45 116 59 263 365 0 34 2
151 p 231 213 95 32 71 33 157 221 0 1 2
157 p 257 221 103 33 84 37 163 229 0 30 2
173 p 284 239 104 34 100 46 173 {239, 240} 3 6 2
191 p 267 262 114 35 80 38 191 {262, 263} 3 4 2
193 p 270 265 116 36 80 38 193 {265, 266} 3 9 2
197 p 461 271 194 56 149 62 337 454 0 1 2
199 p 347 274 161 48 94 44 251 337 0 14 2
211 p 394 287 176 52 108 58 269 361 0 18 2
223 p 432 300 195 52 133 52 313 414 0 25 2
227 p 374 305 180 50 103 41 277 367 0 1 2
229 p 400 309 178 52 118 52 271 365 0 8 2
233 p 347 314 156 47 101 43 233 {314, 315} 3 4 2
239 p 378 321 175 48 105 50 269 361 0 1 2
241 p 331 325 164 48 81 38 241 {325, 326} 3 21 2
251 p 484 336 228 58 142 56 353 462 0 9 2
257 p 367 343 180 50 96 41 257 {343, 344} 3 1 2
--------------------------------------------------------------------------
12 n 93 (N) 28 13 34 18 53 79 0 9 2
0 n 6 5 2 1 3 0 2 2 0 1 2
4 n 180 9 63 26 60 31 109 158 0 10 2
6 n 18 10 4 3 9 2 6 10 0 1 2
8 n 57 18 18 9 17 13 29 47 0 9 2
9 n 176 50 61 24 61 30 107 157 0 4 2
10 n 32 19 8 5 13 6 13 22 0 1 2
15 n 93 34 27 13 35 18 53 79 0 9 2
18 n 146 44 54 20 46 26 89 133 0 28 2
21 n 505 35 178 51 183 93 353 495 0 18 2
22 n 137 36 53 20 44 20 89 128 0 10 2
24 n 82 65 18 11 36 17 47 74 0 6 2
25 n 117 68 35 16 45 21 73 108 0 9 2
26 n 77 73 22 12 29 14 47 72 0 4 2
27 n 54 45 11 7 24 12 27 45 0 4 2
28 n 110 46 44 17 30 19 71 103 0 8 2
30 n 135 51 45 19 45 26 79 121 0 12 2
32 n 132 63 50 23 38 21 83 125 0 22 2
42 n 99 66 25 12 42 20 53 79 0 1 2
44 n 78 69 19 11 33 15 44 69 0 4 2
45 n 167 70 65 24 52 26 109 157 0 28 2
46 n 164 71 65 23 53 23 101 141 0 4 2
48 n 78 74 23 12 29 14 48 74 0 4 2
49 n 79 75 24 12 29 14 49 75 0 4 2
50 n 80 76 25 12 29 14 50 76 0 4 2
51 n 81 77 26 12 29 14 51 77 0 4 2
52 n 82 78 27 12 29 14 52 78 0 4 2
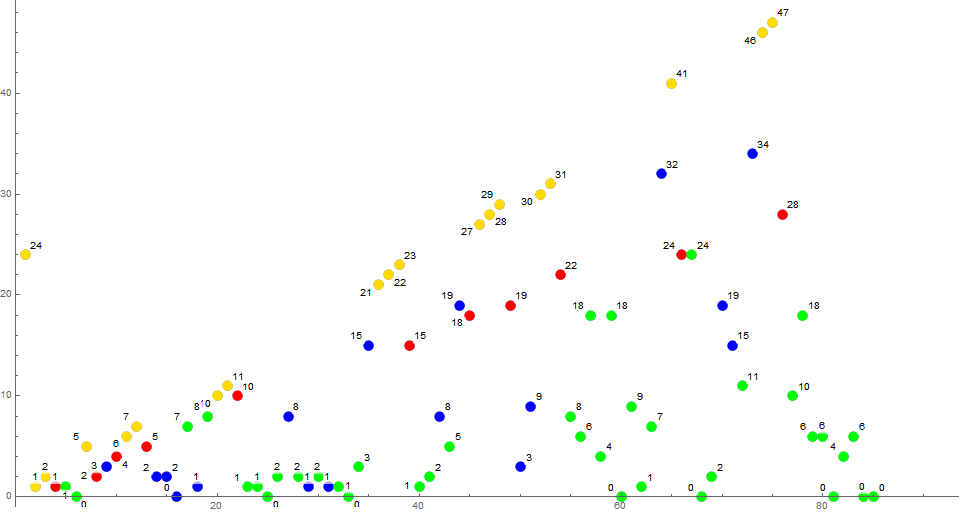
Figure A2: Annotated scatterplot of s2, the canonical prime trajectory, showing the nontrivial terms. The color function addresses the condition instigating the term. Gold indicates a preceding novel nonprime, red a preceding novel prime. Green indicates a preceding extant nonprime, and blue indicates a preceding extant prime. The annotation shows the term m.

Figure A12: Annotated scatterplot of s12, the canonical nonprime trajectory, showing the nontrivial terms. See A2 for color function description.
 Figure A37: Annotated scatterplot of s37, a distinct trajectory that defects from the canonical prime trajectory s2 at n = 59, by influence of 37 being present in the trajectory s2. The initial instance of x = 37 transmutes s(58) to an extant prime rather than novel. See A2 for color function description.
Figure A37: Annotated scatterplot of s37, a distinct trajectory that defects from the canonical prime trajectory s2 at n = 59, by influence of 37 being present in the trajectory s2. The initial instance of x = 37 transmutes s(58) to an extant prime rather than novel. See A2 for color function description.
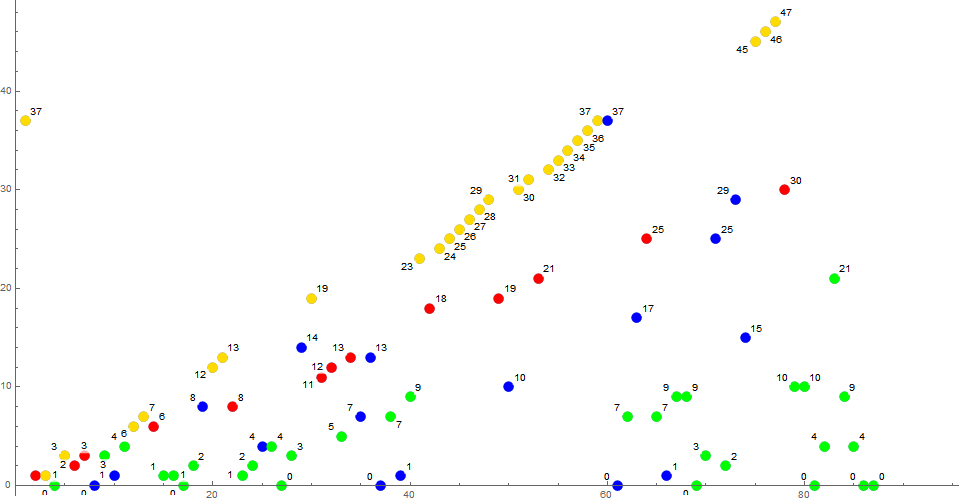
Figure A24: Annotated scatterplot of s24, a distinct trajectory that defects from the canonical nonprime trajectory s12 at n = 66, by influence of 24 being present in the trajectory s12. The initial instance of x = 24 transmutes s(65) to an extant nonprime rather than novel. See A2 for color function description.
Block[{a = {2}, c = 0},
Do[If[And[i > 2, a[[-2 ;; -1]] == {0, 0}], Break[],
If[FreeQ[Most@ a, #],
If[PrimeQ[#],
c++; AppendTo[a, c],
AppendTo[a, i - c]],
If[PrimeQ[#],
c++; AppendTo[a,
Count[a[[-FirstPosition[Reverse@ Most@ a, #][[1]] ;; -2]], _?(! PrimeQ[#] &)] ],
AppendTo[a,
Count[a[[-FirstPosition[Reverse@ Most@ a, #][[1]] ;; -2]], _?PrimeQ] ]]
] &@ a[[-1]] ], {i, Infinity}];
a[[1 ;; -3]]]
Disclosure: throughout my 20s I used the name Icarus > Flemish “de Vlieger” = son of the flyer. This article is not about personal demise! ; )
Document Revision Record.
2021 0311 2200 Draft.