Payload and counter multiplier sequences.
A sequence of David Sycamore.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0620.
Introduction.
We examine a self-referential sequence a conditional regarding the last-generated term m = a(n) = a(k) for1 ≤ k < n, hence is extant, else m is not found in a, hence novel. The novel Condition 0 reports the number of divisors of m, τ(m), while the extant Condition 1 reports the product m × c(m) where c(m) represents the cardinality of m in a(k) for 1 ≤ k < n.
Let a(1) = 1; If m = a(n) is novel, then a(n+1) = τ(m), else a(n+1) =m × c(m).
The sequence a begins:
1, 1, 2, 2, 4, 3, 2, 6, 4, 8, 4, 12, 6, 12, 24, 8, 16, 5, 2, 8, 24, 48, 10, 4, 16, 32, 6, 18, 6, 24, 72, 12, 36, 9, 3, 6, 30, 8, 32, 64, 7, 2, 10, 20, 6, 36, 72, 144, 15, 4, 20, 40, 8, 40, 80, 10, 30, 60, 12, 48, 96, 12, 60, 120, 16, 48, 144, 288, 18, 36, 108, 12, 72, 216, 16, 64, 128, 8, 48, 192, 14, 4, 24, 96, 192, 384, 16, 80, 160, 12, 84, 12, 96, 288, 576, 21, 4, 28, 6, 42, 8, 56, 8, 64, 192, 576, 1152, 24, 120, 240, 20, 60, 180, 18, 54, 8, 72, 288, 864, 24, ...
a(2) = 1 since a(1) = 1 sets a record in a thus, Condition 0 yields τ(1) = 1.
a(3) = 2 since a(2) = a(1) = 1 thus Condition 1 yields 1 × 2 = 2.
a(4) = 2 since a(3) = 2 is new, therefore Condition 0 yields τ(2) = 2.
a(5) = 4 since a(4) = a(3) = 2 so Condition 1 yields 2 × 2 = 4.
a(6) = 3 since a(5) = 4 has never appeared before, so Condition 0 yields τ(4) = 3.
etc.
This sequence can be generated by Code 1.
Figure 1.1 is a log-log scatterplot of a(n) for 1 ≤ n ≤ 212. (Click here for an extended scatterplot of a(n) for 1 ≤ n ≤ 218).
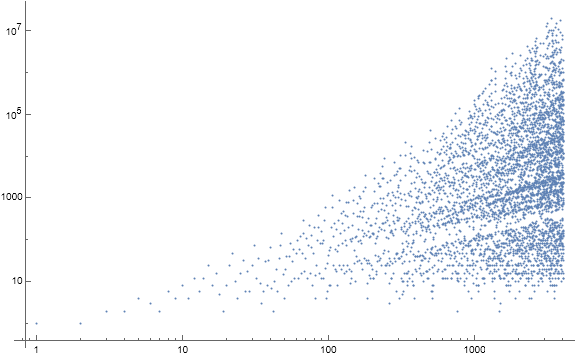
We apply a logarithmic plot because of the multiplicative nature of Condition 1, where m ⇒ mc for 1 ≤ c. Effectively, Condition 0 replaces the Condition 1 product 0m = 0 with a number-theoretical payload function that serves to pare down m.
Let Condition 0 pertain to novel a(n) and let Condition 1 pertain to extant a(n) = a(k) for 1 ≤ k < n.
Records outside the trivial first term result from Condition 1 while local minima result from Condition 0, specifically the occasion of a novel prime p → τ(p) = 2. The absolute minimum of a is 1. The maxima are highly divisible and even outside of 1.
A list of maxima appears below:
1, 2, 4, 6, 8, 12, 24, 48, 72, 144, 288, 384, 576, 1152, 1536, 1728, 3456, 3840, 5760, 8640, 10368, 20736, 41472, 51840, 69120, 103680, 138240, 207360, 259200, 276480, 311040, 345600, 414720, 518400, 622080, 1244160, 1382400, 2073600, 2764800, 4147200, 4354560, 5529600, 6220800, 12441600, 14515200, 19353600, 29859840, 43545600, 52254720, 87091200, 174182400, 232243200, 261273600, 522547200, 1045094400, 1393459200, 2090188800, 2612736000, 2786918400, 5225472000, ...
These appear at the following indices:
1, 3, 5, 8, 10, 12, 15, 22, 31, 48, 68, 86, 95, 107, 139, 150, 180, 228, 236, 241, 314, 339, 497, 658, 701, 740, 790, 998, 1060, 1078, 1131, 1153, 1198, 1272, 1303, 1317, 1645, 1665, 1813, 2321, 2623, 2630, 2670, 3102, 3157, 3367, 4113, 4464, 4847, 5406, 5554, 8041, 8294, 8765, 9086, 10312, 11994, 13278, 13857, 14413, ...
Table 1.1 lists the indices n of novel primes p = a(n). In all cases, of course, 2 follows novel p in a.
i a(n) n a(n+1) n+1
--------------------------
1 2 3 2 4
2 3 6 2 7
3 5 18 2 19
4 7 41 2 42
5 11 762 2 763
6 13 1494 2 1495
7 17 30596 2 30597
8 19 82536 2 82537
...
In the case of a, the least missing m = p(i+1) for ni ≤ k < n(i+1). For 82537 ≤ n ≤ 218, the least missing m is 23. It is not known when 23 will appear in a.
Let sequence s record the conditions deployed by the algorithm behind a:
0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, ...
Therefore, a(1) and a(3) are novel and a(2) is extant i.e., a(2) appears at a(k) for 1 ≤ k < n, namely a(1) = a(2), etc. hence s(1) = s(3) = 0 and s(2) = 1. We can take indices j of 0s or 1s in s to identify the instigating condition that generates a(n+1).
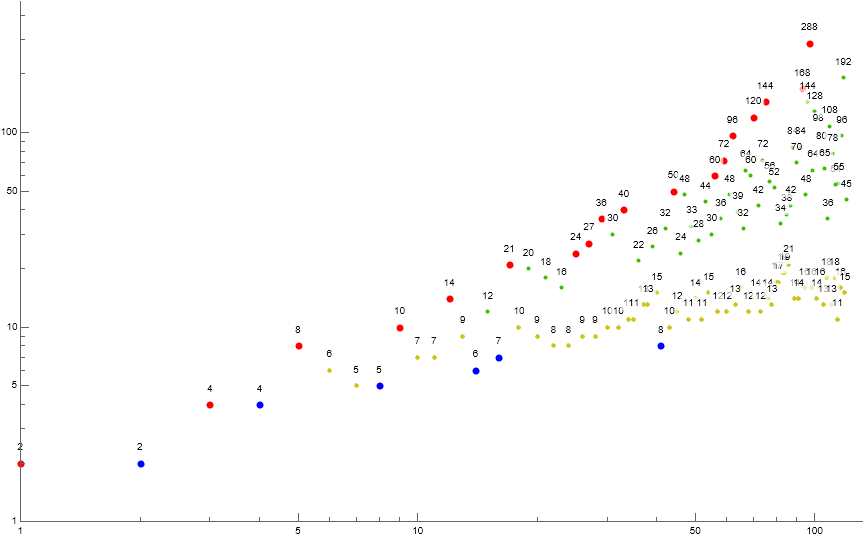
Figure 1.2 is a labeled log-log scatterplot of a(n) for 1 ≤ n ≤ 28. Records a( j) appear in red, local minima in blue, terms instigated by novel m in gold and by extant m in green.
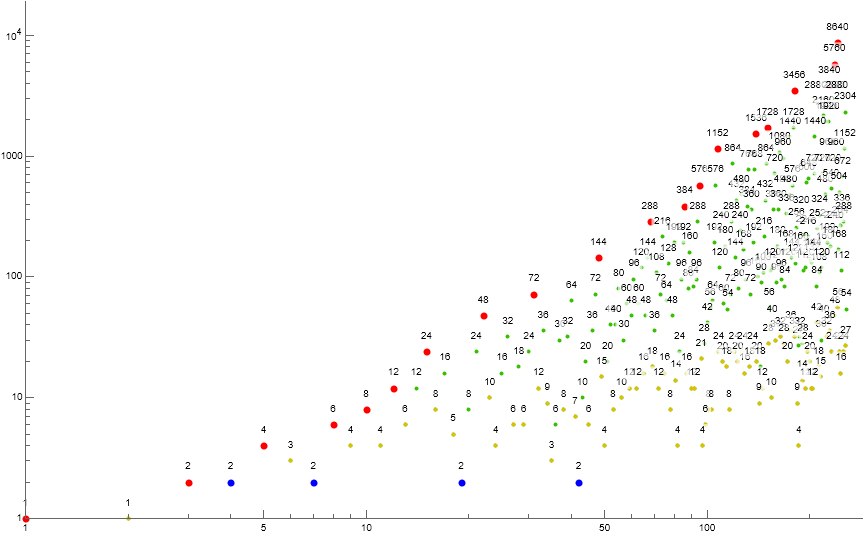
Condition 1 is more prone to repetition than is Condition 0 in a.
Table 1.2 is a list of the first occurence of run length ℓ of consecutive Condition 1 in a. Thus, the run begins at a( j) and a(k) is the occasion of Condition 0 that breaks the run.
ℓ j k a(j) a(k)
-----------------------------------
1 3 4 2 2
2 14 16 12 8
3 20 23 8 10
4 83 87 24 16
5 146 151 108 28
6 367 373 216 64
7 308 315 36 40
8 1875 1883 600 162
9 1309 1318 1080 132
10 1177 1187 54 60
11 5720 5731 810 252
12 5395 5407 1134 432
13 8691 8704 2250 480
14 35117 35131 3000 750
15 40199 40214 5488 924
16 90534 90550 34020 1836
17 64371 64388 7000 1575
18 147995 148013 6860 1920
...
Condition 0 is repeated at the following indices n ≤ 218:
6, 18, 23, 34, 41, 49, 81, 96, 260, 292, 306, 390, 506, 515, 762, 906, 948, 1033, 1067, 1374, 1494, 1504, 1666, 1734, 1907, 2036, 2368, 2473, 2500, 2572, 3444, 3547, 3644, 5165, 5952, 6822, 11029, 11249, 12272, 12398, 12706, 13887, 14386, 14624, 15286, 15610, 17186, 17473, 21337, 23160, 23727, 26590, 30273, 30596, 31262, 33631, 34114, 35735, 37713, 38002, 39587, 40753, 41367, 42098, 49848, 53739, 57469, 59474, 60825, 61692, 65089, 69060, 82079, 82536, 83986, 90358, 94671, 94728, 94890, 102472, 103042, 122083, 129784, 140898, 142795, 143221, 149629, 173712, 185311, 200427, 201027, 228878, 260074, 261659, ...
For n ≤ 218, Condition 0 never appears more than twice consecutively.
The commonest number in the first 2k terms is {1, 1, 2, 2, 2, 6, 8, 12, 12, 12, 24, 24, 24, 24, 24, 24, 24, 24, …}.
Table 1.3 lists the 12 most common terms and their cardinalities in a(1..218):
24 1668
48 1648
96 1475
144 1322
72 1305
32 1184
120 1115
192 1022
16 1003
40 967
240 952
288 925
The term m = 12 is 17th in the list, repeated 725 times. Hence we see that certain terms enjoy hegemony, that is, a range of n over which m is the commonest term in a. There may be a transition zone where m dithers with m' for hegemony. The list above Table 1.3 may not be a complete list of numbers m with hegemony over a, since the intervals were selected arbitrarily on account of being perfect powers of 2.
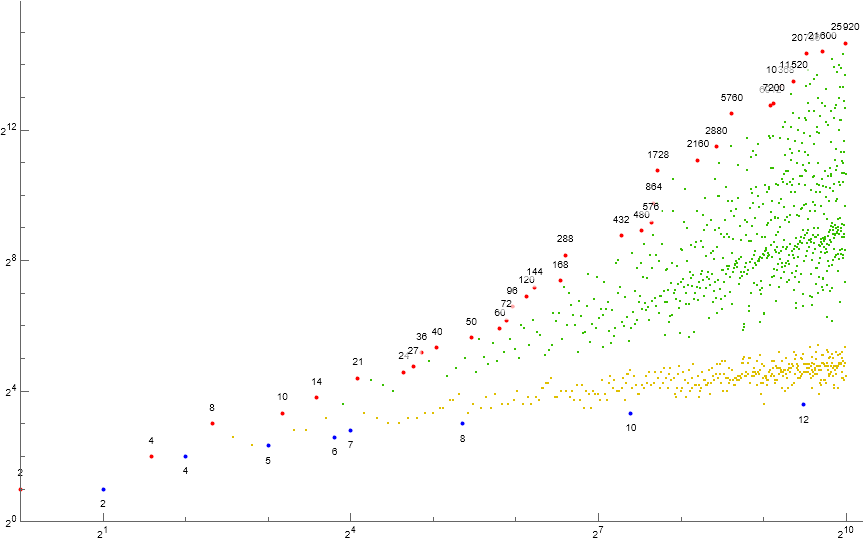
Figure 1.3 is a log-log scatterplot of a(n) for 1 ≤ n ≤ 210. Records a( j) appear in red, zeros in blue, terms instigated by novel m in gold and by extant m in green. The records and occasions of 2 in a are labeled.
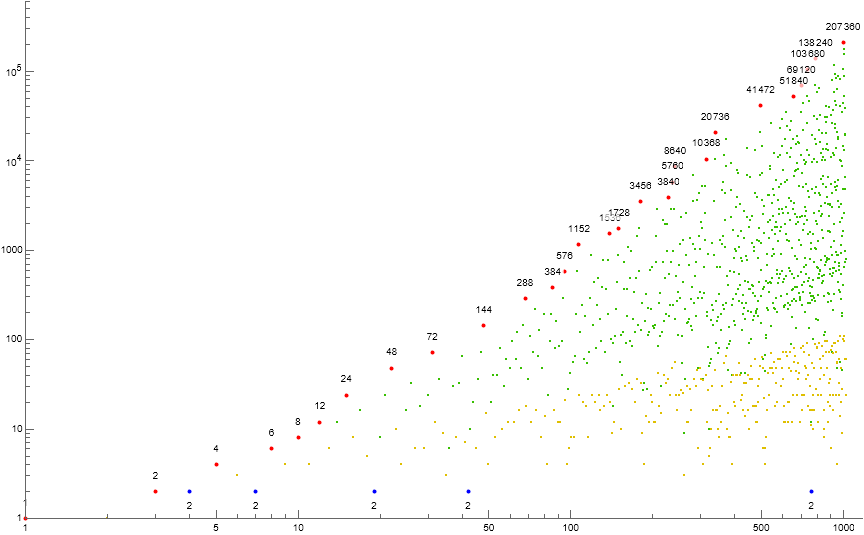
In Figure 1.3 we see that terms m instigated by Condition 0 dominate the lower portion of the plot. Condition 1 echos m above a gap, however, some Condition 1 results appear within the area dominated by Condition 0. There seem to be multiple transformations of m in the plot. The gaps that separate the echos seem to diminish and even move negative such that the echos interfere with one another as n increases. The echo phenomenon warrants further investigation.
Variant based on sum of prime factors with repetition.
We may consider Condition 0 as harboring a payload function f(x) = τ(x). A similar sequence b might be defined using b(1) = 2 and a Condition 0 payload function sopfr(x), that is, OEIS A1414(x), the sum of prime divisors of x with multiplicity.
Let b(1) = 2; If m = b(n) is novel, then b(n+1) = A1414(m), else b(n+1) = m × c(m).
The sequence b begins:
2, 2, 4, 4, 8, 6, 5, 5, 10, 7, 7, 14, 9, 6, 12, 7, 21, 10, 20, 9, 18, 8, 16, 8, 24, 9, 27, 9, 36, 10, 30, 10, 40, 11, 11, 22, 13, 13, 26, 15, 8, 32, 10, 50, 12, 24, 48, 11, 33, 14, 28, 11, 44, 15, 30, 60, 12, 36, 72, 12, 48, 96, 13, 39, 16, 32, 64, 12, 60, 120, 14, 42, 12, 72, 144, 14, 56, 13, 52, 17, 17, 34, 19, 19, 38, 21, 42, 84, 14, 70, 14, 84, 168, 16, 48, 144, 288, 16, 64, 128, 14, 98, 16, 80, 13, 65, 18, 36, 108, 13, 78, 18, 54, 11, 55, 16, 96, 192, 15, 45, ...
b(2) = 2 since b(1) = 2 sets a record in b thus, Condition 0 yields A1414(2) = 2.
b(3) = 4 since b(2) = b(1) = 2 thus Condition 1 yields 2 × 2 = 4.
b(4) = 4 since b(3) = 4 is new, therefore Condition 0 yields A1414(4) = 4.
b(5) = 8 since b(4) = b(3) = 4 so Condition 1 yields 4 × 2 = 8.
b(6) = 6 since b(5) = 8 has never appeared before, so Condition 0 yields A1414(8) = 6.
b(7) = 5 since b(6) = 6 has never appeared before, so Condition 0 yields A1414(6) = 5.
b(8) = 5 since b(7) = 5 has never appeared before, so Condition 0 yields A1414(5) = 5.
etc.
This sequence can be generated by Code 2. We have found 393216 = 218 + 217 terms so as to attempt to ascertain local minima.
Figure 1.1 is a log-log scatterplot of a(n) for 1 ≤ n ≤ 212. (See the full plot of 393216 terms.)
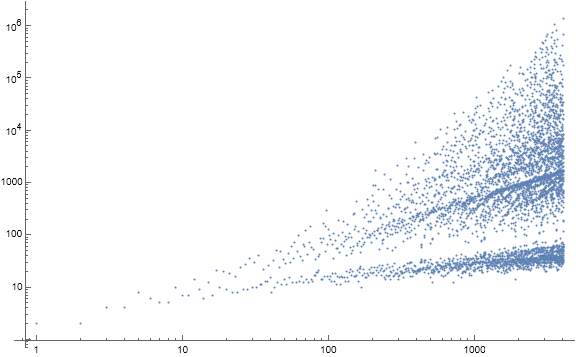
Let Condition 0 pertain to novel b(n) and let Condition 1 pertain to extant b(n) = b(k) for 1 ≤ k < n.
Records outside the trivial first term result from Condition 1 while local minima result from Condition 0. The absolute minimum of a is 2. The maxima are highly divisible and even outside of 1.
A list of maxima appears below:
2, 4, 8, 10, 14, 21, 24, 27, 36, 40, 50, 60, 72, 96, 120, 144, 168, 288, 432, 480, 576, 864, 1728, 2160, 2880, 5760, 6912, 7200, 10368, 11520, 20736, 21600, 25920, 43200, 51840, 57600, 69120, 86400, 103680, 138240, 172800, 207360, 230400, 259200, 311040, 362880, 483840, 518400, 622080, 691200, 725760, 1036800, 1382400, 2073600, 2419200, 2592000, 3628800, 7257600, 8709120, 9676800, ...
These appear at the following indices:
1, 3, 5, 9, 12, 17, 25, 27, 29, 33, 44, 56, 59, 62, 70, 75, 93, 97, 155, 184, 199, 204, 211, 295, 344, 392, 542, 557, 589, 659, 732, 840, 1017, 1038, 1253, 1323, 1469, 1536, 1586, 1697, 1771, 2448, 2581, 2610, 2635, 2846, 2948, 3056, 3129, 3162, 3414, 3530, 4090, 4682, 4884, 5559, 5797, 6069, 6423, 8054, ...
Local minima were generated by negating and reversing b, then taking maxima, hence only the first dozen following indices correspond to bona-fide local minima:
2, 4, 8, 14, 16, 41, 168, 715, 1910, 5119, 23970, 53461, 53778, 157246, 359687, 386730, 392081, 392470, ...
It would seem the indices that exceed 218 might not prove to correspond to actual local minima. We have not yet done more diligence in ascertaining how many indices of local minima are indeed reliable.
Table 2.1 lists the (greatest) index n of local minimum a(n). It may turn out to be true that terms a(n) greater than, say, 30, are also not actual local minima.
i n a(n)
---------------------
1 2 2
2 4 4
3 8 5
4 14 6
5 16 7
6 41 8
7 168 10
8 715 12
9 1910 14
10 5119 18
11 23970 21
12 53461 24
13 53778 25
14 157246 27
15 359687 30
16 386730 39
17 392081 43
18 392470 46
...
The numbers m < 1 and m = 3 never appear in the sequence. Since b(1) = 2 → 2 ⇒ 4 → 4… and since the sum 3 cannot be produced by any combination of prime factors other than 3 itself, m = 3 cannot appear unless the product mc = 3; as 3 is prime, we require m = 3 and c = 1 or m = 1 and c = 3 to furnish 3 as a result of Condition 1. The number m = 1 does not appear in the sequence, hence we will not have 3 in the sequence either. OEIS A670(m) lists the number of ways we can attain the sum m; there is no way to have m = 1 and only a single way to have 2 ≤ m ≤ 4, but for all other primes, there are multiple avenues to have a prime sum. For m = 5, we have 5 ⇒ 5 and 6 = (2 × 3) ⇒ 5. For m = 7, we have 7 ⇒ 7, 10 = (2 × 5) ⇒ 7, and 12 = (2 × 2 × 3) ⇒ 7 (cf. A064364).
We see that novel p → p since the sum of prime factors of p with multiplicity is p itself. Therefore, if a new prime p enters b, it is restated in the following term. The primes p do not enter b in order of their magnitude: b(3631) = 61 while b(4078) = 59.
The following indices n have novel prime b(n):
1, 7, 10, 34, 37, 80, 83, 164, 430, 433, 1111, 1169, 1172, 1906, 2793, 3631, 4078, 4201, 4477, 4595, 5699, 6655, 7234, 9711, 9714, 9977, 10202, 10205, 11064, 15867, 16489, 17498, 17501, 19815, 21157, 21299, 22158, 22161, 23037, 23286, 25943, 25946, 27146, 28958, 28961, 32028, 34906, 37735, 38739, 41363, 42841, 43543, 43829, 43832, 44219, 45355, 46933, 47051, 48540, 49264, 50095, 56539, 57028, 62538, 63994, 65159, 66745, 68668, 70706, 72332, 72968, 73923, 79260, 80902, 81179, 83205, 88221, 88247, 88523, 89674, 91447, 91450, 94919, 97432, 99502, 105006, 105009, 110064, 115383, 115688, 117191, 119323, 120007, 120828, 123232, 123235, 127542, 134984, 134987, 135194, 138983, 144519, 144522, 145879, 147724, 148554, 149007, 149789, 150505, 153731, 157303, 159438, 160600, 160603, 163808, 164672, 165458, 165694, 168015, 177857, 181214, 187001, 190397, 192709, 192813, 195463, 196362, 200453, 200930, 203028, 206856, 208730, 209227, 212305, 213780, 223316, 228104, 228107, 231281, 231284, 231914, 233940, 233943, 236592, 254533, 254536, 262921, 263145, 263148, 263543, 268274, 277670, 278268, 278445, 280541, 280821, 284388, 293472, 295005, 303420, 307460, 309733, 311217, 311552, 314066, 317297, 317300, 323170, 327313, 327316, 335156, 338781, 339161, 346936, 352995, 353153, 355411, 355806, 365911, 386646, 390937, ...
These b(n) include all the primes 2..1201 except 3 and the following:
797, 863, 887, 911, 977, 1019, 1091, 1093, 1097, 1151, 1153, 1171, 1181, 1187, 1193
There doesn’t seem to be a reason to expect these primes p > 3 not to appear in b as n increases.
Let sequence t record the conditions deployed by the algorithm behind b:
0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, ...
Therefore, b(1) and b(3) are novel and b(2) is extant i.e., b(2) appears at b(k) for 1 ≤ k < n, namely b(1) = b(2), etc. hence t(1) = t(3) = 0 and t(2) = 1. We can take indices j of 0s or 1s in t to identify the instigating condition that generates b(n+1).
Figure 2.2 is a labeled log-log scatterplot of b(n) for 1 ≤ n ≤ 27. Records appear in red, local minima in blue, terms instigated by novel m in gold and by extant m in green.
Condition 1 is more prone to repetition than is Condition 0 in a.
Table 2.2 is a list of the first occurence of run length ℓ of consecutive Condition 1 in b. Thus, the run begins at b( j) and b(k) is the occasion of Condition 0 that breaks the run.
i j k b(j) b(k)
---------------------------------
1 3 4 4 4
2 46 48 24 11
3 95 98 48 16
4 201 205 108 19
5 553 558 180 26
6 690 696 162 24
7 1776 1783 567 31
8 3122 3130 540 38
9 1598 1607 162 31
10 6060 6070 1134 47
11 6413 6424 405 47
12 35774 35786 2646 59
13 10734 10747 525 49
14 120872 120886 7546 66
15 57145 57160 3750 60
16 230933 230949 24375 77
17 247042 247059 4375 65
...
For 1 ≤ n ≤ 393216, Condition 0 is repeated twice fairly often (189 occasions), but is repeated thrice only once, instigated by b(5) = 8 → 6 → 5 → 5.
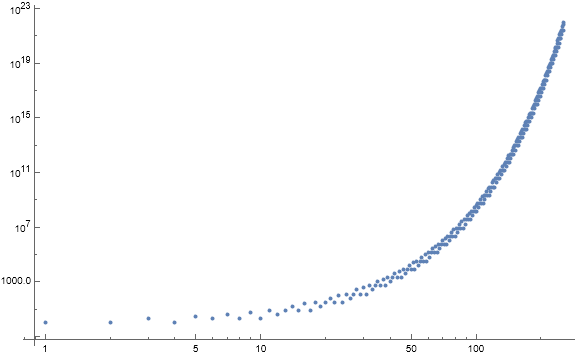
Figure 2.3 is a log-log scatterplot of b(n) for 1 ≤ n ≤ 210. Records appear in red, local minima in blue, terms instigated by novel m in gold and by extant m in green. The records and local minima are labeled.
In Figure 2.3, as in Figure 1.3, we see that terms m instigated by Condition 0 dominate the lower portion of the plot. Condition 1 echos m above a gap. Unlike the plot of a, the plot of b features a more distinct separation between the novel and extant streams. The extended log-log plot exhibits a “feathered” appearance that resembles cirrus clouds. Several diffuse reverberations become apparent as n increases. The regions attributed to novel (gold) and extant (green) conditions remain distinctly separate as n increases. The echo phenomenon warrants further investigation.
The commonest number among the first 2k terms of b is {2, 2, 2, 7, 10, 10, 14, 16, 21, 24, 26, 30, 38, 40, 44, 52, 56, 66, …}.
Table 2.3 lists the 12 most common terms and their cardinalities in b(1..393216):
70 1200
68 1171
67 1169
69 1164
71 1160
66 1160
72 1158
65 1151
64 1129
73 1125
63 1109
74 1095
...
Again, we see that certain terms enjoy hegemony in b over a range of n. There may be a transition zone where m dithers with m' for hegemony. The list above Table 2.3 may not be a complete list of numbers m with hegemony over b, since the intervals were selected arbitrarily on account of being perfect powers of 2.
The tight range of m and their similar populations seem to suggest that the coverage of b ensures all positive m aside from 1 and 3 occur in b, however we have not examined the properties of b as n gets very large.
Variant based on Euler’s totient.
Let’s set the Condition 0 payload function f(x) = φ(x), setting A(1) = 1. Hence:
Let e(1) = 1; If m = A(n) is novel, then A(n+1) = A10(m), else A(n+1) = m × c(m).
The sequence A begins:
1, 1, 2, 1, 3, 2, 4, 2, 6, 2, 8, 4, 8, 16, 8, 24, 8, 32, 16, 32, 64, 32, 96, 32, 128, 64, 128, 256, 128, 384, 128, 512, 256, 512, 1024, 512, 1536, 512, 2048, 1024, 2048, 4096, 2048, 6144, 2048, 8192, 4096, 8192, 16384, 8192, 24576, 8192, 32768, 16384, 32768, 65536, 32768, 98304, 32768, 131072, 65536, 131072, 262144, 131072, 393216, 131072, 524288, 262144, 524288, 1048576, 524288, 1572864, 524288, 2097152, 1048576, 2097152, 4194304, 2097152, 6291456, 2097152, 8388608, 4194304, 8388608, 16777216, ...
These numbers m are interesting because they are perfect powers 2k and 3 × 2k, hence m in A belongs to A029744. We repeat the above data in hexadecimal:
1, 1, 2, 1, 3, 2, 4, 2, 6, 2, 8, 4, 8, 10, 8, 18, 8, 20, 10, 20, 40, 20, 60, 20, 80, 40, 80, 100, 80, 180, 80, 200, 100, 200, 400, 200, 600, 200, 800, 400, 800, 1000, 800, 1800, 800, 2000, 1000, 2000, 4000, 2000, 6000, 2000, 8000, 4000, 8000, 10000, 8000, 18000, 8000, 20000, 10000, 20000, 40000, 20000, 60000, 20000, 80000, 40000, 80000, 100000, 80000, 180000, 80000, 200000, 100000, 200000, 400000, 200000, 600000, 200000, 800000, 400000, 800000, 1000000, ...
Figure 3.1 is a log-log scatterplot of A(n) for 1 ≤ n ≤ 28:
Let “→” indicate Condition 0: φ(m), and let “⇒” indicate Condition 1: m × c(m). Using hexadecimal where the prime decomposition of terms is more evident, the first terms of the sequence proceed as follows:
1 → 1 ⇒ 2 → 1 ⇒ 3 → 2 ⇒ 4 → 2 ⇒ 6 → 2 ⇒ 8 → 4 ⇒ 8 ⇒
10 → 8 ⇒ 18 → 8 ⇒ 20 → 10 ⇒ 20 ⇒
40 → 20 ⇒ 60 → 20 ⇒ 80 → 40 ⇒ 80 ⇒
100 → 80 ⇒ 180 → 80 ⇒ 200 → 100 ⇒ 200 ⇒
400 → 200 ⇒ 600 → 200 ⇒ 800 → 400 ⇒ 800 ⇒
etc.
We see that there are 12 terms in a “preamble” and then the sequence thereafter involves 7-term modules. The sequence is a linear recurrence of order 7, specifically with initial terms (1, 1, 2, 1, 3, 2, 4, 2, 6, 2, 8, 4) and signature (0, 0, 0, 0, 0, 0, 4).
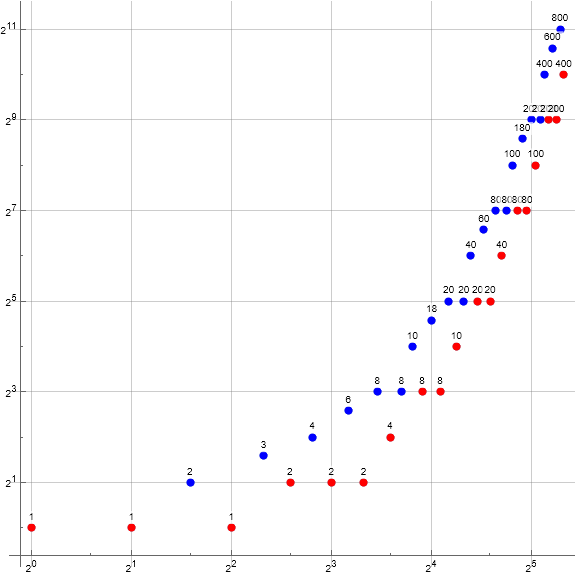
Figure 3.2 is a log-log scatterplot of A(n) for 1 ≤ n ≤ 40 labeling the terms in hexadecimal. Blue terms are instigated by Condition 1 and red by Condition 0:
We recall the formula for Euler’s totient:
φ(n) = ∏_{p | n} (1 − 1/p),
Furthermore, φ(2k) = 2(k − 1) and φ(3 × 2k) = 2k. Thus, if all m are of the form 2k or 3 × 2k, i.e., in A029744, then Condition 0 is tantamount to 2k → 2(k − 1) = m/2 or 3 × 2k → 2k = m/3. The occasion of 1 → 1 and 3 → 2 are special occasions that occur in the preamble.
In the light of this, we may rewrite the progression as follows:
1 (×1)→ 1 (×2)⇒ 2 (÷2)→ 1 (×3)⇒ 3 (×2/3)→ 2 (×2)⇒ 4 (÷2)→ 2 (×3)⇒ 6 (÷3)→ 2 (×4)⇒ 8 (÷2)→ 4 (×4)⇒ 8 (×2)⇒
10 (÷2)→ 8 (×3)⇒ 18 (÷3)→ 8 (×4)⇒ 20 (÷2)→ 10 (×2)⇒ 20 (×2)⇒
etc.
Furthermore we may look only at the operations (decimal):
Preamble: 1 × 1 × 2 ÷ 2 × 3 × 2/3 × 2 ÷ 2 × 3 ÷ 3 × 4 ÷ 2 × 4 × 2 = 16.
Module: m ÷ 2 × 3 ÷ 3 × 4 ÷ 2 × 2 × 2 = 4m.
Hence the preamble brings the sequence to A(12) = 16, for n = 7k + 5, A(n) = 4(k + 1).
As a consequence, no term m repeats more than 4 times in A. The multiplier 2 ≤ c ≤ 4, and the factor c = 3 is undone by the totient of a product of 2 and 3. The sequence A clearly involves m in A029744 and is a linear recurrence.
This concludes our examination.
Appendix:
Block[{a = {1}, c},
Do[If[
IntegerQ@ c[#],
c[#]++; AppendTo[a, # c[#]],
AppendTo[a, DivisorSigma[0, #]]; Set[c[#], 1]] &@
a[[i]], 2^10]; a] ]
Block[{a = {1}, c},
Do[If[
IntegerQ@ c[#],
c[#]++; AppendTo[a, # c[#]],
AppendTo[a, If[# == 1, 0, Total[Times @@@ FactorInteger[#]]]]; Set[c[#], 1]] &@
a[[i]], 2^10]; a] ]
LinearRecurrence[{0, 0, 0, 0, 0, 0, 4}, {1, 1, 2, 1, 3, 2, 4, 2, 6, 2, 8, 4}, 56]
Concerns OEIS sequences:
A000005: The divisor counting function τ(n).
A001414: The sum of prime factors with multiplicity sopfr(n).
A029744: Numbers of the form 2k or 3 × 2k.
A064364: Positive integers sorted by the sum of prime divisors with multiplicity.
Document Revision Record.
2021 0620 2215 (Draft).