The Gorgeous Sequence.
A sequence of David Sycamore.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0623.
Introduction.
Consider a membership-conditional sequence a that reports the divisor counting function τ(m) of a novel most-recent term m, else it reports (m + τ(u)) where u is the least term already in a, thereafter banning such u from being applied again.
Let a(1) = 1; If a(n) ≠ a(k) for 1 ≤ k < n, then a(n+1) = τ(a(n)), else a(n+1) = a(n) + τ(u), where u is a least term a(k) that, once it is used, must be discarded not to be used again. The first condition we call the “novel” condition or Condition 0, and the last we call the “extant” condition or Condition 1.
We define the “hopper” sequence h as a sorted list of terms in a such that its least term h(1) = u; we drop h(1) after deployment in the “extant” condition, with the understanding that the index of s always starts with 1, to maintain h(1) = u. Therefore, the length ℓh increments when the “novel” condition occurs, but remains the same when the “extant” condition plays. In this way, ℓh(n) also represents the number of distinct terms m in a(1..n).
The sequence a begins:
1, 1, 2, 2, 3, 2, 4, 3, 5, 2, 4, 6, 4, 6, 8, 4, 7, 2, 5, 7, 10, 4, 7, 10, 12, 6, 8, 12, 16, 5, 9, 3, 5, 7, 9, 11, 2, 4, 6, 9, 13, 2, 4, 6, 9, 13, 15, 4, 8, 11, 15, 19, 2, 5, 7, 9, 11, 14, 4, 7, 10, 12, 15, 18, 6, 10, 14, 18, 22, 4, 8, 11, 15, 17, 2, 4, 6, 9, 13, 16, 18, 20, 6, 12, 16, 22, 28, 6, 12, 16, 22, 24, 8, 10, 14, 18, 20, 24, 28, 32, 6, 10, 14, 18, 22, 26, 4, 8, 11, 15, 17, 21, 4, 8, 11, 15, 17, 21, 26, 31, 2, ...
a(2) = 1 since a(1) = 1 sets a record in a and is novel, hence τ(m) = τ(1) = 1. We add a(1) to h to have h = {1}.
a(3) = 2 since a(1) = a(2) = 1, hence m + τ(u) = 1 + τ(h(1)) = 1 + τ(1) = 1 + 1 = 2.
We drop h(1) but add a(2) = 1 to h and sort to have h = {1}.
a(4) = 2 since a(3) sets a record in a and is novel, hence τ(m) = τ(2) = 2.
We add a(3) = 2 to h and sort so that h = {1, 2}.
a(5) = 3 since a(3) = a(4) = 2, 1 hence m + τ(u) = 2 + τ(h(1)) = 2 + τ(1) = 2 + 1 = 3.
We drop h(1) but add a(4) = 2 to h and sort to have h = {2, 2}.
etc.
This sequence can be generated by Code 1. The code produces 216 terms in under a minute and 220 terms in a little more than an hour.
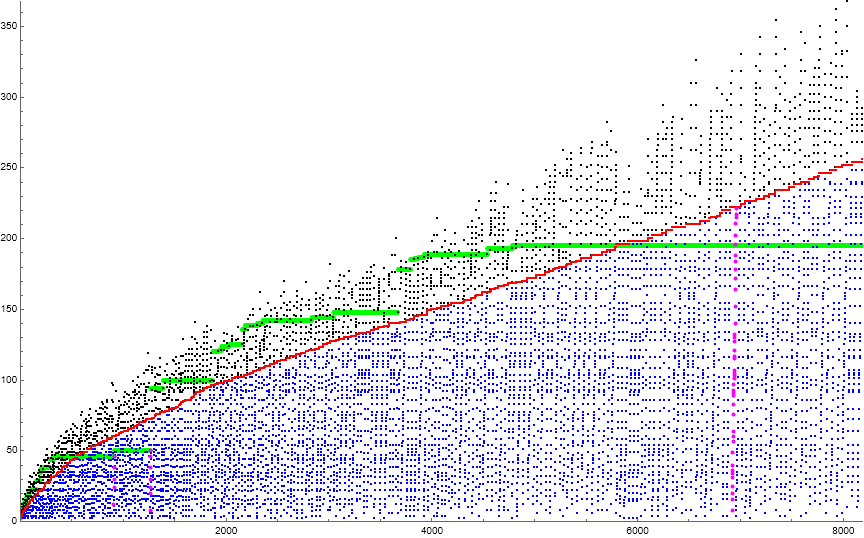
Figure 1.1 is a scatterplot of a(n) for 1 ≤ n ≤ 212. (Click here for a 3840-pixel extended scatterplot of a(n) for 1 ≤ n ≤ 219 and here for same at 6720 pixels for 1 ≤ n ≤ 220).
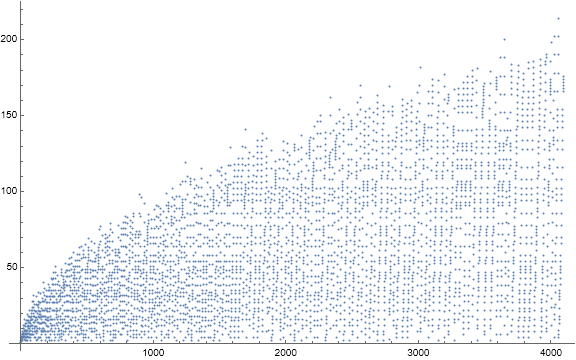
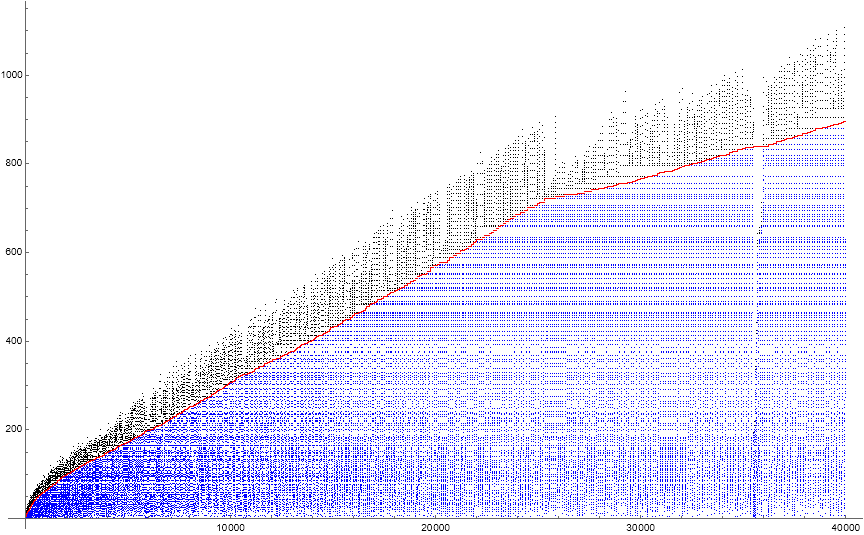
The sequence scatterplot sports several remarkable features that require about 36000 terms to fully express. The sequence can be divided into coterminous subsequences or cycles c(i) that start with a(k) = τ(a(k−1)) of Condition 0, followed by ℓ ≥ 1 instances of Condition 1, and end upon discovery of a novel number M, which is the maximum of c(i).
This paper endeavors to describe all the major features of a(n) for 1 < n < 220:
- The term m = 1 is the minimum and appears precisely twice.
- The effect of Condition 0 is decrease for input m > 2.
- The effect of Condition 1 is increase for all input. For n > 5, Condition 1 yields at least m = 4.
- The length of the hopper sequence h increases with Condition 0 and holds constant with Condition 1.
- The prevailing low L of the hopper sequence h, the maxima of h(1..n), arises on account of the deletion of the least term u = h(1). Any given value L may occur in h with significant multiplicity.
- The sequence is sensitive to the relationship of a(n) to L, since a(n) < L will precede L and require consumption before headway is made against the prevailing low.
- The sequence can be divided into coterminous cycles c(i) = a(k..k+ℓ) where a(k) = τ(a(k−1)) via Condition 0, a(k+1) = (a(k) + τ(L(k+1)) ) through Condition 1.
- Cycles c(i) for i > 2 are strictly increasing.
- If c(i) does not have length ℓ ≤ 2, then a recursion a(n+1) = a(n) + τ(a(n−1)) generates terms until a novel sum M = a(k+ℓ) results. M is the last and largest term of cycle c(i). We see that M(i−1) → τ(M(i−1)), which is the first term of the next cycle.
- The recursion a(n+1) = a(n) + τ(a(n−1)) admits classification of cycles according to signatures taken from their first terms, i.e., (a(k), a(k+1) − a(k)). The signatures can be used to generate pure trajectories and find a least common term m = 422 among the 275 distinct cycle-signatures present in a(n) for n ≤ 220.
- The common term m = 422 divides phase 1 into the “semi-coherent” phase 1a, and the “coherent” phase 1b.
- The prevailing low L serves as the demarcation between phases of cycles.
- M < L results in a “crash”, that is, a cycle that terminates in phase 1 “early”. Most cycles terminate in phase 2 (at least for n ≤ 220). A crashed M means that u < L, the smaller u, the more likely that the next cycle will also crash, producing a conspicuous “gorge” in the scatterplot of the sequence.
- The first crash involves c(84) = a(910..915).
- The first gorge involves c(583..588) = a(35478..35878).
- The least gap g is the smallest m that does not appear in a(1..n). We can split the range m into three regimes as regards conditions. Condition 1 assuredly pertains to 1 ≤ m < g, and Condition 0 assuredly pertains to m > r, where r is the most recent local maximum. For g < m < r, we have Condition 1 most often closer to g, with Condition 0 becoming more likely as m approaches r. For m = g we have Condition 0 and m = r triggers Condition 1.
- Crashes are prohibited for 1 ≤ n ≤ 555 and 1267 ≤ n ≤ 5795 since g(n) > L(n) in those ranges.
- In the scatterplot, a “semi-coherent” subphase (1a) appears below a certain m = 422 and a “coherent” subphase 1b occurs as the cycles mature toward L. The coherent phase (1b) does not manifest until a(14786) = 422, since L(14786) = 422. Hence, we refer to a(14786) = 422 as the “triple point” of the sequence where phases 1a, 1b, and 2 meet.
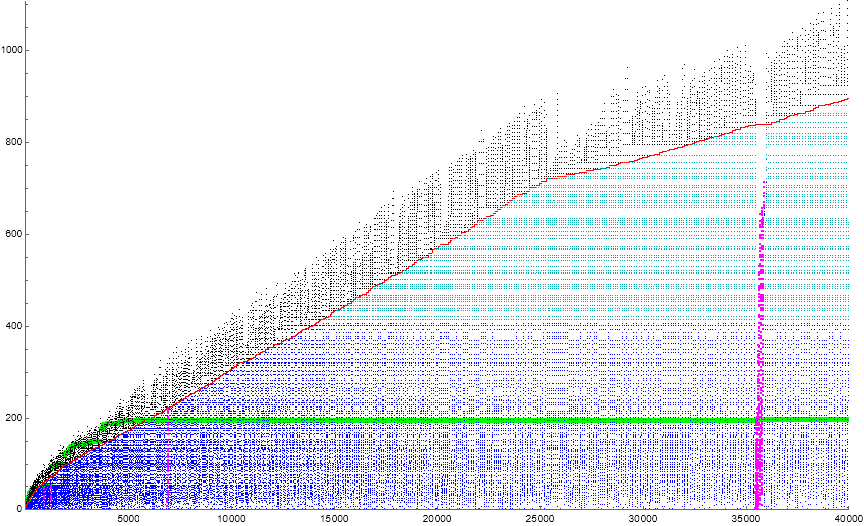
Figure 1.2 is a scatterplot of a(n) for 1 ≤ n ≤ 40000. The green line represents the least gap g(n) and is not actually a feature of a(n). The red line represents the prevailing low L(n), also is not a feature of a(n). Dark blue terms τ(a(k−1)) ≤ m < 422 populate the “semi-coherent” phase (1a) of cycle c(i). Light blue terms 422 ≤ m ≤ L populate the “coherent” phase (1b) of cycle c(i). Black terms m > L populate phase (2) of c(i). Magenta terms constitute a “crashed” cycle that has g ≤ M < L; multiple consecutive crashed cycles constitute a “gorge”. In crashed cycles, we have only phase (1). The “triple point” of the graph, where we first have phase (1b) appears to be a(14478) = 414, but is in actuality (given 220 terms) a(14786) = 422.
Parity.
Because we apply the divisor counting function τ(n) in both conditions, we should bear in mind some general properties of τ(n). Chiefly, that for 1 ≤ |n| ≤ 2, τ(n) = n, else τ(n) < |n|; τ(0) is undefined. Also, odd τ(n) requires n be a product of prime powers pe for p prime and e even. This is because τ(n) = ∏ (e + 1). Specifically, perfect squares n yield odd τ(n). This would tend to make odd m rare in a.
Observation 2.1: For 1 ≤ n ≤ 220, odd m are precluded from phase (1a) for 229 < m < 414 and entirely from phase (1b) in non-crashed cycles. Some odd m > 229 appear in phase (2) and in crashed cycles.
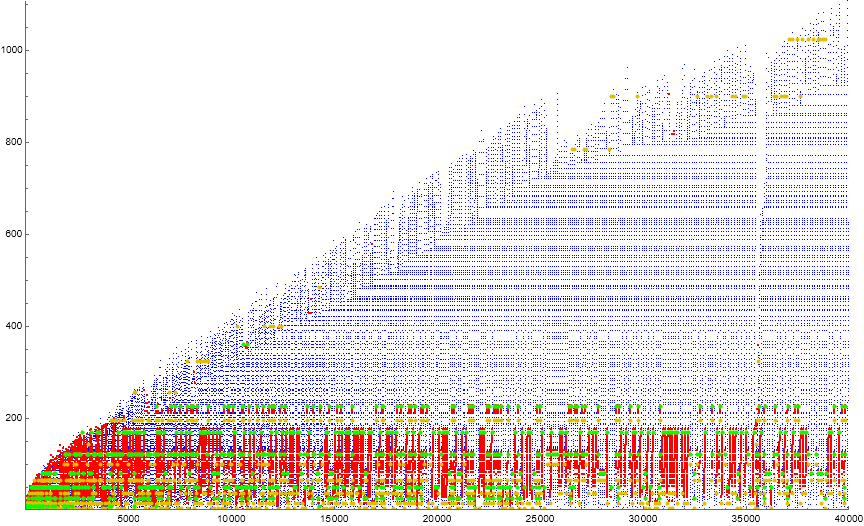
Figure 2.1 is a scatterplot of a(n) for 1 ≤ n ≤ 40000 generally plotting even terms m in blue, even terms m with odd τ(m) in gold, odd m in red, and odd m with odd τ(m) in green.
Local maxima and minima.
The records transform r of a begins:
1, 2, 3, 4, 5, 6, 8, 10, 12, 16, 19, 22, 28, 32, 34, 40, 43, 47, 51, 53, 56, 57, 60, 63, 64, 65, 69, 75, 77, 79, 80, 84, 86, 98, 99, 102, 105, 107, 119, 129, 130, 141, 143, 146, 150, 162, 170, 182, 188, 200, 202, 214, 220, 226, 232, 240, 248, 252, 262, 264, 268, 282, 294, 310, 326, 330, 342, 354, 362, 368, ...
The indices of the records are:
1, 3, 5, 7, 9, 12, 15, 21, 25, 29, 52, 69, 87, 100, 138, 176, 233, 252, 265, 338, 371, 384, 400, 447, 459, 492, 515, 594, 606, 677, 779, 794, 850, 896, 1100, 1144, 1204, 1225, 1243, 1584, 1674, 1700, 2214, 2239, 2265, 2338, 2568, 3014, 3621, 3652, 4027, 4058, 4437, 4464, 4584, 4625, 5111, 5201, 5281, 5460, 5559, 5710, 6251, 6523, 6573, 7015, 7200, 7353, 7939, 8045, 8295, 8559, 8974, 9370, 9644, 9770, 9950, 10000, ...
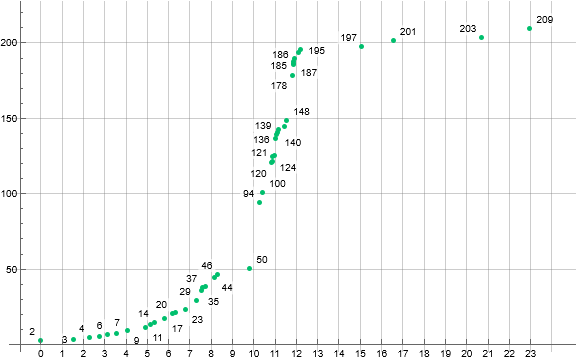
It is clear that the first two terms a(1) = a(2) = 1 are the only occasions of 1 in the sequence. The term m can be novel only upon its first occasion in a, thereafter it is extant. Thus, we have only one occasion of Condition 0 applied to m = 1 → τ(1) = 1. Since 1 is the initial term and since the range of the divisor counting function consists of the positive integers, we can have no input less than 1. Since h is assembled from terms in a, its least term u ≥ 1. Because m ≥ 1 and Condition 1 involves the sum (m + τ(u)) where both terms are at least 1, the local minima thus result from novel p → τ(p) = 2. Therefore, the minimum of the sequence a is 1, but for n > 2, m = 2 is the smallest possible term, preceded by a prime p new to a.
Records r → τ(r) via the novel Condition 0 since by definition, r is novel.
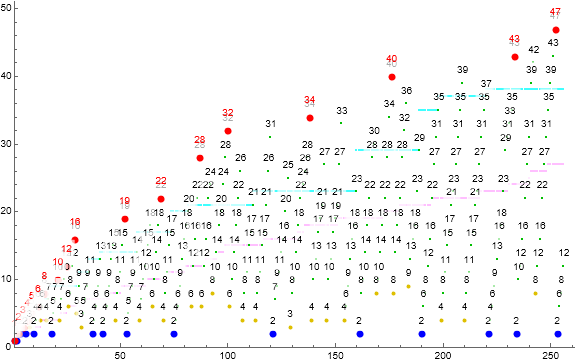
Figure 3.1 is a labeled scatterplot of a(n) for 1 ≤ n ≤ 27. Records a( j) = r appear in red, local minima in blue, terms instigated by novel m in gold and by extant m in green. The magenta line indicates the smallest number m not in a(1..n). (Click here for a gridded, detailed plot of a(n) for 1 ≤ n ≤ 210.)
 .
.
The least gap g.
Let the least gap g(n) be the smallest m > 0 not (yet) represented in a(1..n). The sequence is a step-function that begins:
2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 7, 7, 7, 7, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 11, 11, 11, 11, 11, 13, 13, 13, 13, 13, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 17, 20, 20, 20, 20, 20, 20, 20, 20, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 21, 23, 23, 23, ...
Appendix Table A lists the least index n for which g(n) is distinct from g(n − 1).
We may divide the range m into three regions. For 1 ≤ m < g, where g is the least m missing from a, we are assured Condition 1, thus, the sum (m + τ(u)). For m > r where r is the (most recent) local maximum, we are assured Condition 0 thus τ(r). For g ≤ m ≤ r, we may have either condition, though Condition 1 is more likely for m closer to g, and Condition 0 more likely for m closer to r. Of course, for m = g, we have Condition 0, and for m = r we have Condition 1.
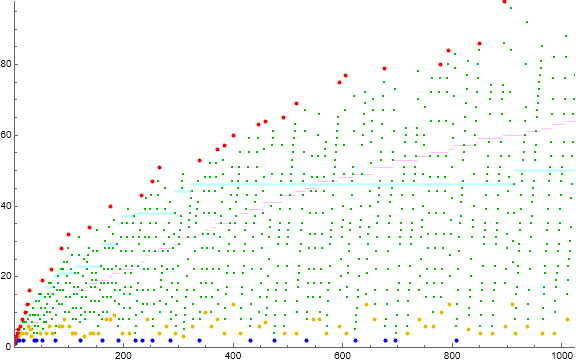
Figure 3.2 is a scatterplot of a(n) for 1 ≤ n ≤ 213, showing the least gap g(n) in green, the prevailing low L(n) of the hopper sequence in red separating phase (1) with u < L in blue from phase (2) in black. Crashed cycles c(i) whose last and largest term g ≤ M < L appear in magenta.
The least gap g has implications for the possibility of crashed cycles c(i) wherein the greatest cycle term M < L, the prevailing low. Crashes are prohibited for 1 ≤ n ≤ 555 and 1267 ≤ n ≤ 5795 since g(n) > L(n) in those ranges. Since 1 ≤ m < g(n) exists in a, only Condition 1 is available, hence M cannot be the largest term in the cycle, a contradiction.
It seems that crashes are possible for n > 5795 given the apparently stalled growth of g while L continues to increase, but we have not proved that there are any further prohibitions of crashes.
Figure 3.3 is a labeled plot of distinct g(n) for 1 ≤ n ≤ 220, with a logarithmic index n. The index axis is labeled e for n = 2e.
Observation 3.1: We see that g(325..913) = 46, representing a significant plateau, followed by more progress until g(4785..35502) = 195, g(35502..98364) = 197, and g(98365...) = 201.
Conjecture 3.1: g(n) should prove “sticky” as n increases, since the only source of missing, predominantly odd m derives from crashes where the terms are neither semi-coherent nor coherent. The situation may prove stickier as m > 414 reluctantly enter sequence a, since m = 414 divides the coherent phase (1b) from the semi-coherent phase (1a) below for n ≥ 14478.
For a(1..98365), the least missing m include are:
201, 203, 207, 209, 213, 227, 237, 239, 241, 245, 247, 249, 253, 255, 257, 259, 263, 265, 267, 269, 271, 273, 277, 279, 281, 283, 285, 287, 289, 291, 293, 295, 297, 299, 303, 305, 307, 309, 311, 313, 315, 317, 319, 321, 323, 325, 327, 329, 331, 333, 335, 337, 339, 341, 343, 345, 347, 349, 351, 355, 363, 367, 369, 371, 373, 375, 377, 379, 381, 383, 385, 387, 389, 391, 393, 397, 399, 401, 403, 405, 407, 409, 411, 413, 415, 417, 419, ...
The smallest missing even m = 540. The bolded numbers in the list above have entered a(1..220), and for n = 220, the smallest even m = 664 that is missing in a.
Hence, g(n) should tend to jump if the run of a distinct g is very large as the aggregated action of crashes tends to fill in missing mas n increases. If 201 enters a and all numbers in the above list remain missing, g will move to 203, however, it is possible that 203 enters a before 201.
Are there any m that are absolutely prohibited, even in the coherent phase (1a) range? It would seem that the occasion of odd sums (a(n) + τ(a(n−1))) becomes more likely and numerous as the cycle length ℓ increases.
The prevailing low L in the hopper sequence h.
The hopper sequence h has a nondecreasing length as n increases, since we place a(n) into h after performing either condition function, maintaining a sorted h in any case, whether or not a(n) = a(k) for k < n. However, if a(n) = a(k) for k < n, we report the sum (a(n) + τ(u)) = a(n+1), then discard u = h(1), exposing h(2) and subtracting 1 from the indices of h. There may be multiple copies of a given value m in h. 2. Hence, the length of h increases by 1 after Condition 0 but remains the same after Condition 1.
Suppose we have a least term L > 1 in h, i.e., L = h(1). If a(n) > L, then a(n) would be placed after L in h. If a(n) = L, then L would have multiplicity in h. If a(n) = u < L, then u would replace L as the first term in h and would demand application upon the next occasion of Condition 1 to be discarded. We bank copies of a given m in h whenever the same number m ≥ u. These copies appear consecutively in h. The exhaustion of repeated copies of u is evident in the nearly-vertical consistent spacing of black points in phase (2) above the red line (indicating L(n)) in Figure 3.2.
The subduction of u < L occurs often (i.e., probably all the time) when Condition 0 reports τ(m), a relatively small number. Even if we have the occasion of consecutive repeated Condition 0, the result is the placement of a small number of u < L that must be consumed before the prevailing low L is itself eventually consumed and thereafter increases.
If as usual, Condition 0 furnishes τ(m) < g(n), we have Condition 1 follow. Condition 1 repeats so long as a(n) = a(k) for k < n, and since for n > 2, m ≥ 2 and τ(m) is at least 2, a(n) increases to M, a novel term, necessitating Condition 0.
During the consecutive repetition of Condition 1, we have the function (a(n) + τ(u)) become (a(n) + τ(a(n−1))), since a(n−1) becomes the least term u = h(1). Therefore u is consumed in the making of the next term until u ≥ L, and we begin making headway against the multiplicity of the number L in h until Condition 1 yields a novel term M.
Let novel M ≥ g be the largest and last term in a cycle c(i). The occasion of M < L governs crashing of a cycle and may precipitate a gorge in the scatterplot. We explain the reason for this in a section below.
The sequence L begins:
1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 16, 16, 16, 16, ...
This is the maxima transform of the sequence u:
1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 2, 4, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 5, 5, 3, 5, 7, 7, 7, 2, 4, 6, 7, 7, 2, 4, 6, 7, 8, 8, 4, 8, 8, 9, 9, 2, 5, 7, 9, 9, 9, 4, 7, 9, 9, 10, 10, 6, 10, 10, 10, 10, 4, 8, 11, 11, 11, 2, 4, 6, 9, 11, 11, 12, 12, 6, 12, 12, 12, 12, 6, 12, 13, 13, 13, 8, 10, 13, 14, 14, 14, 15, 15, 6, 10, 14, 15, 15, 15, 4, 8, 11, 15, 15, 15, 4, 8, 11, 15, 16, 16, 16, 16, ...
The prevailing low L demarcates phase (1) behavior (both semi-coherent and coherent) from phase (2) of cycle c(i). In phase (1) we are consuming u < L, but in phase (2), a(n) > L, hence we store it after L in h, and in the following occasion of Condition 1 we consume L instead. Since L often appears with significant multiplicity, the consumption of u < L and that of L yields distinctive patterns in the scatterplot and is responsible for the different appearance of these phases evident given thousands of terms of a.
Figure 3.4 is a scatterplot of a(n) for 1 ≤ n ≤ 210. Records a( j) = r appear in red, local minima in blue, terms instigated by novel m in gold and by extant m in green. The cyan line indicates g(n), while the magenta line indicates L(n). (Click here for a gridded, detailed plot of a(n) for 1 ≤ n ≤ 210.)
Runs of Condition 1 delimited by instances of Condition 0.
Let Condition 0 pertain to novel a(n) and let Condition 1 pertain to extant a(n) = a(k) for 1 ≤ k < n. Condition 0 features the transform m → τ(m), while Condition 1 has m ⇒ (m + τ(u)), the latter consuming u = h(1), both conditions slipping m into h such that it appears in order of magnitude, that is, h remains sorted such that the smallest number appears first at h(1) = u.
Let sequence b record the conditions deployed by the algorithm behind a:
0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, ...
Therefore, a(1) and a(3) are novel and a(2) is extant i.e., a(2) appears at a(k) for 1 ≤ k < n, namely a(1) = a(2), etc. hence b(1) = b(3) = 0 and b(2) = 1. We can take indices n of 0s or 1s in b to identify the instigating condition that generates a(n+1).
Cycles c(i).
We note that for 1 ≤ n ≤ 220, Condition 0 is never repeated in adjacent terms, however, Condition 1 often repeats. Indeed, we may break a into subsequences or “cycles” c(i) such that begin with the result m → τ(m), followed by instances of Condition 1 that proceed until a novel M is discovered, instigating Condition 0 and starting a new cycle. M is the last and greatest term in cycle c(i) and instigates Condition 0 that yields the first term τ(M) of the next cycle.
Let a(k) = τ(a(k−1)) be the first term of cycle c(i), where a(k−1) = M(i−1) is a novel term that ends the previous cycle c(i−1) and is its maximum. Let ℓi be the length of cycle c(i), thus a(k+ℓ) = Mi.
The term a(k) is the fruit of Condition 0, but all the rest of the terms in the cycle are results of Condition 1. In other words, c(i) consists of 1 term (the first) resulting from Condition 0 and (ℓ−1) terms resulting from Condition 1. The term a(k+1) = (a(k+1)+ τ(L(k))) because the number a(k) = τ(a(k−1)), a(k) < L, has not yet entered the hopper sequence h to supplant L as least term u. If ℓ ≥ 1, that is, if a(k+2) is not novel, thereafter, the consequence of a(k) → u is that for a(k+2 … k+ℓ), the action of Condition 1 is a recursion of (a(n)+τ(a(n−1))). The cycle strictly increases as n increases to discover a novel M = a(k+ℓ) and end the cycle. Hence M is the largest term in cycle c(i).
The term following M → τ(M) is the first term of cycle c(i+1). We note that M > τ(M) for M > 2, otherwise M = τ(M) in positive integers. (The sequence a is fully positive.)
Figure 4.1 joins terms m in cycles c(i) for 1 ≤ i ≤ 27, showing cycles with even i in red and odd i in blue.
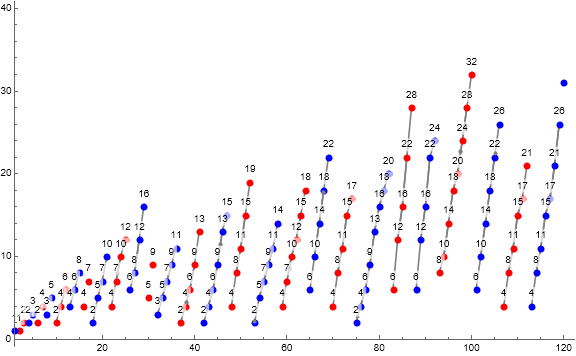
The cycle c(i) is the building block of the sequence a.
It is easy to see that we cannot have repeated Condition 0 for 1 ≤ m ≤ 2 since τ(m) = m, hence m is already in the sequence and always triggers Condition 1.
Conjecture 4.1: Condition 0 is never repeated consecutively in a.
If Condition 0 were repeated, it would seem to need to occur while n is small. We temper this statement with the observation that the least gap g seems to stick. It could be possible to have τ(m) > g, but we would require g to stick long enough for us to have highly divisible m sufficiently large to furnish an enormous number of divisors. In the case of a repeated Condition 0, we simply would interpret each instance as a crashed cycle with ℓ = 1 as τ(m) = M < L.
What is necessary for Condition 0 to repeat is for m → τ(m) new to the sequence, and we see that g(n) > τ(a(n)) for 1 ≤ n ≤ 220. The value τ(a(582418)) = 60 is the greatest in this range, but by then, g(582418) = 201. We see that it might be possible that g(n) ≤ τ(a(n)), but m such that τ(m) > 201 requires a number as large as A2182(36) = 554400, while the largest term in a(1..220) is 6890. Therefore, g = 201 would have to hold such that 554400, a term very much larger than the largest of 1048576 terms, could enter a, a sequence generated by an iterative run of sums of previous terms and the divisor counting function of other terms already in a. It would seem that, by the time 554400 enters a, g would prove much higher, however, it may be that there are long-missing (usually odd) m in a and indeed, we then might see a repeated Condition 0.
Figure 4.2 is a scatterplot of a(n) for 1 ≤ n ≤ 40000 showing the 2 phases of cycles of the sequence. Phase (1) appears in blue below the red line indicating the prevailing low L of the hopper sequence h, and phase (2) appears above in black.
Let’s examine the phases of a cycle.
Phase 1.
We divide a cycle into two phases. Phase (1) has u < L and involves the Condition 1 sum (a(n) + τ(a(n − 1))) after the first term a(k) of the cycle, as a consequence. Hence u derives from terms m in the cycle rather than the prevailing low L. The prevailing low L is held constant until m > L and thereafter, when the copies of the same L are exhausted.
A cycle will eventually discover a novel term M > g, certainly if M sets a record in a. If M ≥ L, we enter phase (2), otherwise the cycle is said to “crash”. This means that u never exceeds L as we move to a new cycle. Certain crashes affect subsequent cycles such that they also crash; this produces a “gorge” in the scatterplot. We will explain crashes and gorges in a section below.
Phase 2.
Phase (2) begins when u ≥ L, hence we make headway against the multiplicity of L, consuming the copies until we increase L or we discover a novel M. The difference between the phases is only evident given thousands of terms of a. The consequence of the different appearances is more than cosmetic, because the frequent patterns in phase (1) mean that certain m appear in a while others do not, thereby affecting the possibility of novel m, the termination of cycles, the least gap g, and the possibility and occasion of crashes.
Signatures of cycles.
We may identify the cycle c(i) with a signature ( a(k), a(k+1) − a(k) ) as this reliably instigates the same recursion and produces the same trajectory for cycles with the same signature. In this paper the algorithms we use state the signature as “4+4”, that is, a(k…k+1) = {4, 8}, thus signature (4, 4).
Because we enter the recursion (a(k) + τ(a(k − 1))) from a(k+2) through the duration of phase (1), that is, until a(n) > L, the first two terms of c(i) produce the same terms. For instance, the signature 4+4 generates the following infinite trajectory:
4, 8, 11, 15, 17, 21, 23, 27, 29, 33, 35, 39, 43, 47, 49, 51, 54, 58, 66, 70, 78, 86, 94, 98, 102, 108, 116, 128, 134, 142, 146, 150, 154, 166, 174, 178, 186, 190, 198, 206, 218, 222, 226, 234, 238, 250, 258, 266, 274, 282, 286, 294, 302, 314, 318, 322, 330, 338, 354, 360, 368, 392, 402, 414, ...
The trajectory of signature 4+4 includes the term 414, as does many of the trajectories that appear in a. The number m = 414 divides phase (1) into a “semi-coherent” subphase (1a) m < 414, and a “coherent” phase (1b) m ≥ 414. We note that a(10112) = 414 and is its first occasion hence in phase (2), but the first phase (1) appearance is a(14478).
For 1 ≤ n ≤ 220, the 3247 cycles fall into 275 distinct cycle signatures. Of the 275, only {4+32, 8+40, 32+30, 32+40, 48+4, 48+30} do not include 414. The major parameters of cycle signatures appear in this text file.
Of the 275 cycle signatures for 1 ≤ n ≤ 220, 90 appear just once, 18 of these are extinct before i = 385. The commonest signature is 8+8, repeated 216 times. Signatures with small coefficients tend to appear for the first time for small i.
Some signatures are more prevalent in a certain domain of i, but some appear more or less regularly throughout a.
Coherency of terms m in Phase 1.
The scatterplot of a shown in Figure 4.2 shows an apparently regular spacing of terms in the cycles c(i) of a. What is the “spacing”? Indeed, since we are in mid cycle, we are talking the recurrent instances of the sum (a(n) + τ(a(n − 1))). The nature of the divisor counting function prefers even values.
We recall that τ(n) is most often even, and only odd iff all prime power divisors pe | n have even exponents e, i.e., iff n is a perfect square. The occasion of perfect squares among n is increasingly rare as n increases. Therefore the cycle prefers even terms. Many even numbers occur in the trajectories of all signatures. The effect is to produce two subphases in phase 1.
The range of phase (1a) includes a(k) ≤ m < min(414, L). It exhibits many configurations of even first differences, i.e., τ(a(n − 1)). The action of the divisor counting function in the sequence results in the agreement of all the main signatures on a set of mostly even terms and produces a “semi-coherent” zone in the scatterplot.
The range of phase (1b) appears to be 414 ≤ m < L and only appears in cycles c(i) with i ≥ 385. Most of the signatures common to a in the sequence’s first 220 terms include 414. The sequences that include 414 feature terms m > 414 that are common to most, hence a conspicuously “coherent” subphase.
The effect of coherent m in the cycles of a is that the terms in cycles tend to land on the same m. Hence the gaps in the range are unlikely to be filled unless something throws the cycle out of the usual signatures that have played in a. If a signature occurs that is distinct from the usual signatures, the trajectory of the cycle has a greater chance of hitting a gap and ending in phase (1).
We note that if phase (1b) is truly coherent, this implies that all terms in the phase are even and not perfect squares. If there is a perfect square in the trajectory of any cycle in phase (1b), it will likely crash unless the m in its trajectory already appeared in phase (2) in a previous cycle.
Crashes.
The sequence a comprises cycles c(i) that start with a term a(k) that is the fruit of Condition 0 (i.e., a(k) = τ(M), where M is the previous cycle’s last and maximum term). In the case of c(1), the predecessor of a(2) is given. Condition 1 persists until discovering a novel sum (m + τ(u)) = M. The usual case is that Condition 1 carries M such that it meets or exceeds the prevailing low L. Therefore the usual condition is that a cycle has both phase (1) and phase (2).
However, this is not always the case. At times, g ≤ M < L, meaning that the cycle ends “early” during phase (1) before u ≥ L. In the scatterplot the crashes appear conspicuously short of the phase (2) “fuzz” that dominates the top of the graph. Since L occurs after u in the hopper sequence h for the duration of a crashed cycle, it holds constant.
We have shown under Figure 3.2 that crashes are prohibited for 1 ≤ n ≤ 555 and 1267 ≤ n ≤ 5795 since g(n) > L(n) in those ranges.
The first instance of a crash is c(84) = a(910..914) = {12, 24, 30, 38, 46}, hence signature 12+12, with L(914) = 60. The cycle is also the first instance of signature 12+12 in a.
Hence it seems that the cycle blazes a new trail up through m, finding m = 46 which was missing in a. Indeed, m = 46 was the least gap g(913) in a; when 46 entered a, g(914) = 50.
The effect of the crashed cycle on the ensuing cycle is that the terms m potentially have a smaller spacing based on the number of divisors of u < L added to m. The spacing difference is much less pronounced than for the cycles in A345147.
The cycle discovers a gap in the range m “early”. Since this m is not among the usual suspects, there is a good chance a new signature starts, and the terms of such do not align with the well-trod trajectories, making it likely that we again suffer a crash. Multiple adjacent crashes represent a “gorge”.
It is evident that the signatures that include 414 must have presented extant m because these had first appeared in phase (2) of previous cycles. Therefore, the 414-bearing signatures must share a set of preferred m with those terms in phase (2), otherwise they would also present crashes early in the sequence. This has not been investigated.
A crash doesn’t necessarily derive from a new signature. In fact, the initial crash of a gorge often results from signature 4+32, which does not include 414. Subsequent crashes in a gorge involve long dormant signatures that arise primarily when n is small. Hence the latter trajectory had never played in a, usually presenting novel m < L.
An exhaustive study of the crashes c(i) in a appears in a text file here. The table shows index, gorge numeral, initial index k, run length ℓ, the first and last 3 terms, and the value of the prevailing low L(k+ℓ) so as to compare it to the last term of c(i), M.
Attempts to understand the triggering of a crash.
We have found that we can use a checksum of the form of the sum S of m (mod 2) such that m ≤ 414, where S itself is taken (mod 2). Most cycles have even S, but initial gorge crashed cycles seem to have odd S.
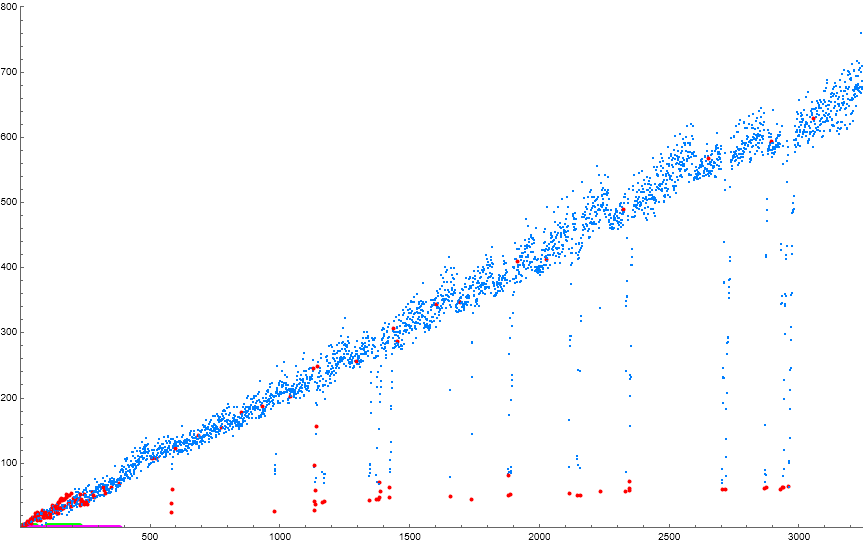
Figure 4.3 is a scatterplot of ℓ(i) for 1 ≤ i ≤ 3247, showing cycles c(i) such that S = 0 in blue, but accentuating those with S = 1 in red. We note that crashes are prohibited in the range of the green lines at the lower left near the origin, and that the term 414 does not appear in phase (1) until i = 385, therefore the magenta line indicates a domain we must ignore. We note that all the gorges feature S = 1.
The sensitivity of the sequence a to rare odd results of the divisor counting function interested us in studying the configuration of perfect square m in the cycles.
We can generate pure trajectories of cycles via the recursion of (w + τ(v)) beginning with the initial terms (a(k), a(k+1)). We can convert the cycle-signature x+y into the initial terms using (x, x+y) = (a(k), a(k+1)). Knowing that this sequence a is sensitive to m = 414, and that it appears that the trajectories seem to converge upon 414 (at least in the domain 1..220), we are only interested in the first couple dozen terms of these trajectories. It is interesting that it appears no squares occur for phase (1b) m > 414 as evidenced by the coherent zone in the large-scale scatterplot of a. Squares surely appear in phase (2), but their presence there is better understood and expected.
We find the perfect squares a(k), counting those that do not exceed 414 to produce a square-signature. The square signature is the decimal equivalent of the binary compactification of √(a(k)). The square-signature 0 pertains to a cycle trajectory that involves no perfect square m < 414.
For instance, given cycle-signature 16+20, we have initial terms {16, 36}. Then we have the trajectory:
16, 36, 41, 50, 52, 58, 64, 68, 75, 81, 87, 92, 96, 102, 114, 122, 130, 134, 142, 146, 150, 154, 166, 174, 178, 186, 190, 198, 206, 218, 222, 226, 234, 238, 250, 258, 266, 274, 282, 286, 294, 302, 314, 318, 322, 330, 338, 354, 360, 368, 392, 402, 414, 422, ...
There are 4 perfect squares {16, 36, 64, 81}, and taking their square roots, we have {4, 6, 8, 9}. We convert these roots to a binary number by mapping 2(R−1) and obtaining 23 + 25 + 27 + 28 = 8 + 32 + 128 + 256 = 424.
We can then classify the 3247 cycle-signatures according to their square-signatures. There are 39 distinct square-signatures for the cycles in a for 1 ≤ n ≤ 220. Of the 39 distinct square-signatures, 17 square-signatures 10, 74, 76, 288, 386, 388, 424, 4106, 4114, 4116, 4130, 4176, 4224, 25632, 25826, 25850, and 25853 pertain to a single cycle signature. The square-signature 0 pertains to 58 cycle-signatures.
The common cycle-signature trajectory T.
The smallest number common to all 275 square-signatures currently pertaining to a(n) for 1 ≤ n ≤ 220 is 422. Hence, taking into account the 6 rare cycle-signatures (4+32, 8+40, 32+30, 32+40, 48+4, 48+30), the actual demarcation between phase (1a) and phase (1b) is m = 422. The presence of m = 414 in the balance of the signatures only appears to be the demarcation.
The trajectory T common to all 275 cycle-signatures begins:
422, 434, 438, 446, 454, 458, 462, 466, 482, 486, 490, 502, 514, 518, 522, 530, 542, 550, 554, 566, 570, 574, 590, 598, 606, 614, 622, 626, 630, 634, 658, 662, 670, 674, 682, 686, 694, 702, 706, 722, 726, 732, 744, 756, 772, 796, 802, 808, 812, 820, 832, 844, 858, 864, 880, 904, 924, 932, 956, 962, 968, 976, 988, 998, 1010, 1014, 1022, 1034, 1042, 1050, 1054, 1078, 1086, 1098, 1106, 1118, 1126, 1134, 1138, 1158, 1162, 1170, 1178, 1202, 1210, 1214, 1226, 1230, 1234, 1250, 1254, 1264, 1280, 1290, 1308, 1324, 1336, 1342, 1350, 1358, 1382, 1390, 1394, 1402, 1410, 1414, 1430, 1438, 1454, 1458, 1462, 1476, 1484, 1502, 1514, 1518, 1522, ...
These are the terms m seen in the “coherent” phase (1b) region of the scatterplot of the sequence a. The first differences are:
12, 4, 8, 8, 4, 4, 4, 16, 4, 4, 12, 12, 4, 4, 8, 12, 8, 4, 12, 4, 4, 16, 8, 8, 8, 8, 4, 4, 4, 24, 4, 8, 4, 8, 4, 8, 8, 4, 16, 4, 6, 12, 12, 16, 24, 6, 6, 4, 8, 12, 12, 14, 6, 16, 24, 20, 8, 24, 6, 6, 8, 12, 10, 12, 4, 8, 12, 8, 8, 4, 24, 8, 12, 8, 12, 8, 8, 4, 20, 4, 8, 8, 24, 8, 4, 12, 4, 4, 16, 4, 10, 16, 10, 18, 16, 12, 6, 8, 8, 24, 8, 4, 8, 8, 4, 16, 8, 16, 4, 4, 14, 8, 18, 12, 4, 4, 16, 4, 4, ...
Distinct first differences given 216 terms of T are:
4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 72, 80
The smallest 216 terms of T are even and T is free of perfect squares. Can it be proven that all m ∈ T are even and not perfect squares?
We note that a(10252) = 422, but a(14786) in cycle c(389) is the first occasion of 422 = L. Therefore the “triple point” of Figure 1.2 is in a slightly different place than it would seem.
Are there future signatures that would induce us to move the demarcation between phase (1a) and (1b) to, say, m = 434 or m = 438, numbers that are also in the common trajectory?
Gorges.
The reason for examining the square signatures is to determine the similarity (semi-coherency) of terms m < 422 in the cycles and attempt to understand the follow-on crashes in a series of adjacent crashes we call “gorges”. We might understand that a given crashed cycle ends early with M < L. Why would this tend to cause the following cycle to crash as well?
The occasion of perfect square m in the cycle trajectory introduces odd addends to the recursive Condition 1 sum (a(n) + τ(a(n−1))). The odd addends may induce the cycle to fill a gap with M < L and end the cycle, since odd numbers are rare in a.
Conjecture 4.2: Gorges, or adjacent crashed cycles, arise from the introduction of small M = a(k+ℓ) → τ(M) → (τ(M) + τ(a(k+ℓ−1))), thereby ushering small coefficients in the cycle-signature (τ(M), τ(a(k+ℓ−1))). If M = a(k+ℓ) is small, then a(k+ℓ−1) < a(k+ℓ) since Condition 1 has generated both, and is an additive function that has a minimum difference of +4. Since small m have decreased access to large τ(m), it is likely that the cycle-signature is small and has not appeared in a for a while. Hence we discover a second low M < L.
As a consequence of a given cycle-signature C to introduce a missing m, the next occasion of C will have a longer trajectory. Eventually, the crash-prone signature C (e.g., 4+32) will perhaps meet L and no longer produce a crash, unless L is faster-growing than the frequency of C in a.
The affect of gorges on the least gap g and missing values m in general is to increase the former and fill in some of the latter.
Table 5.1 lists the gorge that begins at cycle c(i), its signature (a(k), a(k+1) − a(k)), the cycle’s starting index k, and the cycle length ℓ.
i sig. k ℓ
--------------------------------
84(I) 12+12 910 4
102(II) 8+12 1261 6
259(III) 8+8 6920 40
583(IV) 4+32 35478 24
981(V) 4+32 98340 25
1132(VI-A) 4+32 130440 27
1137(VI-B) 4+32 130924 36
1163(VII) 4+32 136081 38
1171(VIII) 4+32 137249 40
1346(IX) 4+32 181994 41
1373(X) 4+32 188010 43
1382(XI) 4+32 189550 44
1423(XII) 4+32 199767 47
1657(XIII) 4+32 273426 48
1740(XIV) 32+40 302228 43
1880(XV-A) 4+32 354289 50
1890(XV-B) 4+32 356111 51
2116(XVI) 4+32 449364 52
2146(XVII) 32+30 461204 49
2158(XVIII) 32+30 464776 50
2234(XIX) 4+32 499839 55
2333(XX) 4+32 547444 56
2347(XXI) 4+32 552523 57
2704(XXII-A) 4+32 742074 58
2719(XXII-B) 4+32 746311 59
2869(XXIII) 4+32 828866 60
2931(XXIV-A) 48+4 861280 59
2936(XXIV-B) 8+40 863163 61
2941(XXIV-C) 8+40 865069 62
2961(XV) 8+40 872005 63
...
Table 5.2 lists the gorge that begins with cycle i, assigned the Roman numeral designation, then all the signatures of cycles in the gorge. Gorges I, II, and III consist of a single-cycle.
84(I) 12+12
102(II) 8+12
259(III) 8+8
583(IV) 4+32 -> 8+2 -> 4+4 -> 2+6 -> 12+8 -> 10+24
981(V) 4+32 -> 2+8 -> 4+8 -> 18+16 -> 12+18 -> 20+24
1132(VI-A) 4+32 -> 6+4 -> 2+4 -> 21+6 -> [4+8]...
1137(VI-B) 4+32 -> 2+2 -> 6+20 -> 12+6 -> 4+12 -> 9+12 ->
8+4 -> 10+8
1163(VII) 4+32 -> 6+6 -> 2+12 -> 18+4 -> 8+8
1171(VIII) 4+32 -> 2+2 -> 2+6 -> 24+12 -> 6+12 -> 24+6
1346(IX) 4+32 -> 4+2 -> 2+4 -> 8+6 -> 10+8 -> 16+24 ->
18+8 -> 4+12 -> 8+12 -> 10+8
1373(X) 4+32 -> 4+6 -> 12+2 -> 12+12 -> 4+20 -> 6+4 ->
12+8
1382(XI) 4+32 -> 2+4 -> 2+20 -> 4+6 -> 4+32 -> 2+6 ->
4+4 -> 12+6 -> 20+12 -> 6+16 -> 6+8
1423(XII) 4+32 -> 2+2 -> 4+4 -> 6+12 -> 20+8 -> 6+4 ->
12+4 -> 12+6 -> 4+12 -> 10+32 -> 4+12 -> 8+24 ->
6+12
1657(XIII) 4+32 -> 8+2 -> 4+2
1740(XIV) 32+40 -> 4+8 -> 6+12 -> 8+16 -> 10+4 -> 4+10
1880(XV-A) 4+32 -> 4+4 -> 3+12 -> 6+8 -> 24+6 -> 6+8 ->
4+6 -> 6+4 -> 18+8 ->[24+24]...
1890(XV-B) 4+32 -> 4+4 -> 2+4 -> 4+8 -> 8+10 -> 2+8 ->
8+6 -> 12+24 -> 24+6 -> 10+8 -> 14+4
2116(XVI) 4+32 -> 4+4 -> 4+6 -> 4+8 -> 12+15 -> 20+4 ->
6+8 -> 16+4 -> 12+4 -> 20+24 -> 6+18 -> 24+16
2146(XVII) 32+30 -> 2+4 -> 2+4 -> 6+8 -> 16+8 -> 36+8 ->
4+12 -> 24+4 -> 24+24
2158(XVIII) 32+30 -> 2+2 -> 24+12 -> 16+8 -> 12+24
2234(XIX) 4+32 -> 2+2
2333(XX) 4+32 -> 12+2 -> 4+2 -> 12+8 -> 6+24 -> 6+12 ->
30+8 -> 12+24 -> 12+8
2347(XXI) 4+32 -> 2+12 -> 2+4 -> 4+4 -> 16+8 -> 18+12 ->
6+12 -> 12+20 -> 36+6 -> 24+16 -> 30+4 -> 36+16 ->
16+4
2704(XXII-A) 4+32 -> 4+2 -> 4+8 -> 4+10 -> 2+8 -> 16+16 ->
8+24 -> 12+4 -> 12+12 -> 28+4 -> 12+16 -> 28+8 ->
12+4 -> 24+32 ->[16+24]...
2719(XXII-B) 4+32 -> 2+4 -> 2+8 -> 18+8 -> 8+4 -> 2+16 ->
4+20 -> 18+4 -> 24+10 -> 6+4 -> 6+24 -> 12+16 ->
24+12 -> 12+12 -> 12+8 -> 12+24 -> 12+8 -> 12+12 ->
48+16 -> 16+16
2869(XXIII) 4+32 -> 4+2 -> 8+4 -> 4+4 -> 8+8 -> 4+32 ->
2+4 -> 4+2 -> 12+24 -> 12+12 -> 32+12 -> 12+16
2931(XXIV-A) 48+4 -> 4+2 -> 12+6 -> 10+16 ->[12+4]...
2936(XXIV-B) 8+40 -> 4+4 -> 2+12 -> 36+6 ->[18+16]...
2941(XXIV-C) 8+40 -> 2+4 -> 4+2 -> 16+8 -> 4+18 -> 4+8 ->
12+4 -> 16+4 -> 12+16 -> 12+8 -> 6+8 -> 16+12 ->
8+16 -> 24+10 -> 6+16 -> 12+4
2961(XXV) 8+40 -> 8+2 -> 2+8 -> 6+4 -> 16+4 -> 12+4 ->
4+20 -> 2+6 -> 2+12 -> 16+24 -> 12+4 -> 12+10 ->
12+8 -> 6+8 -> 16+8 -> 30+20 -> 12+12 -> 16+8 ->
6+16 -> 12+16 -> 12+36 -> 20+8 -> 12+12 -> 12+16
...
In some gorge crash cases, we have signatures following the first crash that have not appeared in a for a while. It seems to stand to reason that these signature trajectories hadn’t played out fully, especially if they appeared before i = 389 when 422 enters a in phase (1). This would seem to make finding a missing m more likely.
Phase 2 provenance of the common trajectory T.
The occasion of the crash-prone C = 4+32 seems to imply that phase (2) does not cover its terms, that it is “off the grid” with regard to the distinct and primarily even terms m that phase (2) yielded for smaller n. That the trajectory of 4+32 may have squares that usher a trajectory that discovers m missing in the phase (2) population at smaller n.
Having found a common trajectory T common to the 275 signatures, we might see that for m < g and m ≥ 422, phase (1a) isn’t the only limiting factor. In fact, if m hadn’t entered a in a previous phase (2), it would trigger a crash by definition, since L is the demarcation between the phases, and therefore m < L. Thus, the terms m generated by Phase (2) must appear in T, and in the union of semi-coherent terms in phase (1a). If this is not true, then we would see m in T triggering crashes, that is, the regular operation of phase (1b) would trigger M < L and end a cycle early.
For 1 ≤ n ≤ 220, the greatest prevailing low is L(1048248) = 6362. This admits the smallest 580 terms m of T; all these terms first appear in phase (2). Hence, phase (2) seems to cover T before any collision in phase 1b can be had.
It would stand to reason that phase (2) would cover T, since we often see the repetition of τ(u) where u is constant over a finite range. Of course, for prime u, we would have the repeated addition of 2, squared prime u would space terms in phase (2) by 3, and squarefree semiprime u would introduce the repeated addition of 4. Therefore we would see gaps (just with these values) perhaps only at ±1 (mod 6), not taking into account the value of the addend m in Condition 1. Therefore the exit from phase (1) furnishes m in phase (2) upon which oftentimes repeated addition of small numbers serves to cover at least many even m. This coverage might prove sufficient to ensure that all m in T are covered by the time L increases to admit m into phase (1b).
Figure 5.1 is a scatterplot of a(n) − L(n) for 1 ≤ n ≤ 40000, i.e., the phase (2) terms of a less the prevailing low L of the hopper sequence h. The plot suggests the coverage of even m ahead of the phase (1b) manifestation of m in T ensures that the so-called “coherent” subphase does not involve m in T finding gaps and ending the cycle before M ≥ T.
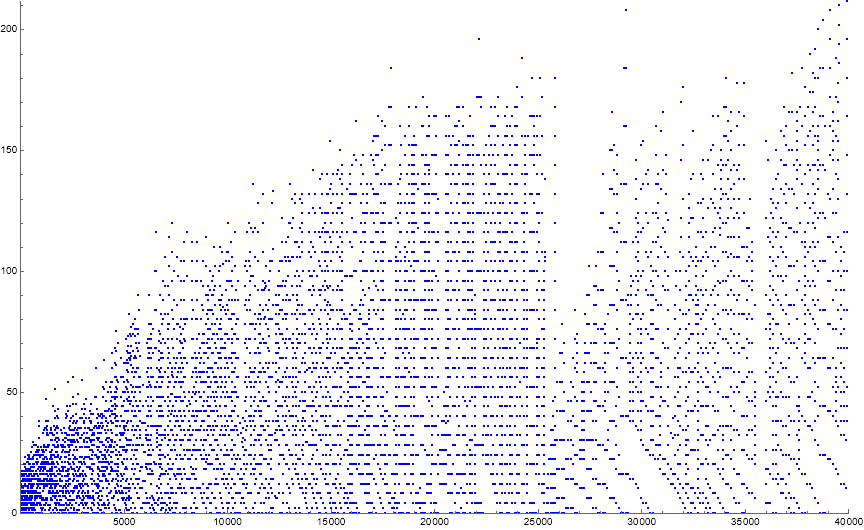
Indeed, the question remains, does phase (2) always cover even m such that m in T are assured to already be in a during a later phase (1b)? Also, is T assuredly always free of perfect squares and thus, always even? How does T assuredly avoid perfect squares?
Conclusion.
We have described a dozen principal features of the sequence s20210622 = a as stated above. These include the nature of the cycle and its relationship to the prevailing low, the conditions of the algorithm, and the manifestation of crashes. We have described the three subphases of a cycle. We have examined crashes and gorges and classified the cycles into signatures taken from their first two terms. For 1 ≤ n ≤ 220, these 3247 cycles belong to 275 distinct cycle-signatures. The cycle signatures feature recurrent trajectories that admit as many as 20 possible squares that would introduce m that potentially might not appear in a and trigger a crash. Six cycle-signatures appear to be responsible for the crashes that have occured in the first million terms. The cycle-signatures further belong to one of 39 distinct square-signatures. We have examined a trajectory T whose least term is 422, common to all 39 square signatures present for 1 ≤ n ≤ 220. We have shown that the smallest 580 terms of T first appear in a on account of phase (2), hence we surmise that phase (2) covers even m in T before they might appear in phase (1b) and trigger a crash. We have seen that a crash featuring a particularly low M yields a signature with low coefficients that kicks off a following cycle that is also prone to crash, creating a gorge.
Open questions exist; chief among them:
- Are all m > 0 in a?
- Are all T even, i.e., are there any squares in T?
- Are there only 39 distinct square-signatures and 275 cycle-signatures for a?
- Does the least gap exceed the prevailing low for n > 220?
- What is the reason for the reduction in the rate of change of the prevailing low around n = 26000?
This concludes our examination.
Appendix:
Table A: Index n ≤ 220 of the first instance of a distinct least gap g > 0 in a:
n g(n)
-----------
2 1
3 3
4 5
5 7
6 9
7 12
9 17
11 31
13 36
14 41
17 58
20 74
21 82
23 112
29 160
35 189
37 198
38 220
44 294
46 325
50 914
94 1267
100 1389
120 1872
121 1927
124 1957
125 2032
136 2155
139 2184
140 2302
142 2358
144 2835
148 3047
178 3672
185 3794
186 3832
187 3873
189 3924
193 4543
195 4785
197 35502
201 98365
...
Block[{a = {1}, h = {}},
Do[
If[FreeQ[#2, #1],
AppendTo[a, DivisorSigma[0, a[[-1]]] ],
AppendTo[a, a[[-1]] + DivisorSigma[0, First[h]] ];
Set[h, Rest@ h]] & @@ {First[#1], #2} & @@ TakeDrop[a, -1];
Set[h, Insert[h, a[[-2]], LengthWhile[h, # < a[[-2]] &] + 1]], 120]; a]
Concerns OEIS sequences:
A000005: The divisor counting function τ(n).
A002182: a(n) The highly composite numbers, i.e., indices of records of τ(n).
Document Revision Record.
2021 0627 2215 (Draft).