The Sailboat Sequence.

A sequence of David Sycamore.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0628.

Introduction.

Let s(1) = 1; If s(n) = s(k) for 1 ≤ k < n , then s(n+1) = c(s(n)) where c(m) is the cardinality of m in s(1..n − 1), else s(n+1) = s(s(n)+1).

Sycamore’s concept uses offset 0, hence s(0) = 1, etc., but hereinafter we shall use offset 1 so as to avoid computational error associated with the use of lists in Mathematica. Because of this, the definition is slightly different from Sycamore’s, and the indices should be decremented if one is interested in the original offset.

The sequence s begins:

0, 0, 1, 0, 2, 1, 1, 2, 1, 3, 0, 3, 1, 4, 2, 2, 3, 2, 4, 1, 5, 1, 6, 1, 7, 2, 5, 1, 8, 1, 9, 3, 3, 4, 2, 6, 1, 10, 0, 4, 3, 5, 2, 7, 1, 11, 3, 6, 2, 8, 1, 12, 1, 13, 4, 4, 5, 3, 7, 2, 9, 1, 14, 2, 10, 1, 15, 2, 11, 1, 16, 3, 8, 2, 12, 1, 17, 2, 13, 1, 18, 4, 6, 3, 9, 2, 14, 1, 19, 1, 20, 5, 4, 7, 3, 10, 2, 15, 1, 21, 1, 22, 6, 4, 8, 3, 11, 2, 16, 1, 23, 1, 24, 7, 4, 9, 3, 12, 2, 17, 1, ...

s(2) = 0 since s(1) = 0 sets a record in a (hence is new) and s(0 + 1) = 0.
s(3) = 1 since s(2) = s(1) = 0; m = 0 appears once in s(1..1).
s(4) = 0 since s(3) = 1 sets a record in a (hence is new) and s(1 + 1) = 0.
s(5) = 2 since s(4) = s(2) = s(1) = 0; m = 1 appears 2 times in s(1..3).
etc.

This sequence can be generated by Code 1. We have generated 2¹⁸ terms.

Figure 1.1 is a scatterplot of s(n) for 1 ≤ n ≤ 2⁸. Red points are records, large gold points are the result of Condition 0, large blue are zeros, and green are fruits of Condition 1. Click for a scatterplot of s(n) for 1 ≤ n ≤ 2¹⁸.

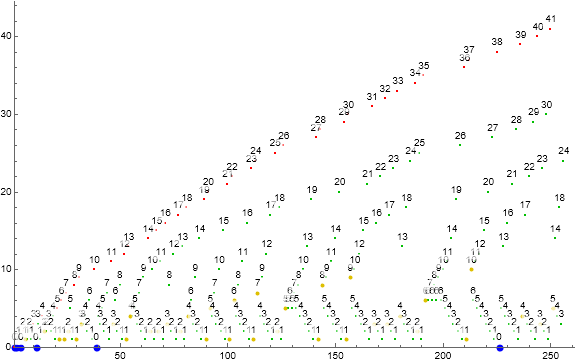
Figure 1.2 is a scatterplot of s(n) for 1 ≤ n ≤ 2¹⁶.

Let b(n) = 1 if s(n) = s(k) for k < n else let b(n) = 0. Hence we have a characteristic function of the occasion of m in s at a smaller index. The sequence b begins:

0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, ...

It is evident that we have many runs of 1s but 0 is singleton. Taking the indices k₀ of 0 in b, we have:

1, 3, 5, 10, 14, 21, 23, 25, 29, 31, 38, 46, 52, 54, 63, 67, 71, 77, 81, 89, 91, 100, 102, 111, 113, 122, 126, 141, 143, 154, 156, 167, 173, 179, 187, 191, 210, 212, 225, 236, 244, 250, 260, 264, 285, 287, 302, 308, 320, 324, 347, 349, 366, 368, 385, 393, 401, 411, 417, 431, ...

The first differences ℓ are:

2, 2, 5, 4, 7, 2, 2, 4, 2, 7, 8, 6, 2, 9, 4, 4, 6, 4, 8, 2, 9, 2, 9, 2, 9, 4, 15, 2, 11, 2, 11, 6, 6, 8, 4, 19, 2, 13, 11, 8, 6, 10, 4, 21, 2, 15, 6, 12, 4, 23, 2, 17, 2, 17, 8, 8, 10, 6, 14, 4, 27, 2, 19, 4, ...

Maxima and minima.

Records R are common and the list of records is that of the nonnegative numbers. The indices of records R_i are:

1, 3, 5, 10, 14, 21, 23, 25, 29, 31, 38, 46, 52, 54, 63, 67, 71, 77, 81, 89, 91, 100, 102, 111, 113, 122, 126, 141, 143, 154, 156, 167, 173, 179, 187, 191, 210, 212, 225, 236, 244, 250, 260, 264, 285, 287, 302, 308, 320, 324, 347, 349, 366, 368, 385, 393, 401, 411, 417, 431, ...

Hence the records represent the sole manifestation of novel m. In other words, if s(n) ≠ s(k), then s(n) has set a record, the previous record is s(n) − 1, and the next s(n) + 1.

We see that R_i ≡ k₀, since records m represent the only novel m in s. Hence (ℓ − 1) represents the run lengths of Condition 1 in s. We might partition s into subsequences t(i) = s(k…k+ℓ), where k is an index of a zero in b, i.e., k ∈ k₀.

We know that there cannot be adjacent records m, since records are novel, thus trigger Condition 0 which reports s(m + 1). For m = s(1) = 0, we report s(0+1) = 0. Once we have adjacent identical m, the novel report s(m + 1) < m. As a consequence, we cannot have adjacent records, and s(n) < n.

The minimum of s is 0. Zeros appear at indices {1, 2, 4, 11, 39, 226, 3636, 257943, …}.

Table 1.1 lists the index i for s(i) = 0, and the novel instigator s(i−1) → 0.

     i  s(i-1)
-------------
     1      -
     2      0
     4      1
    11      3
    39     10
   226     38
  3636    225
257943   3635
...

We see that the numbers 1 + {0, 1, 3, 10, 38, 225, 3635, 257942, …} are indices of 0, the result of the Condition 0 report of s(m + 1), and hence merely reflections of the very first zero, s(1) = 0.

Thus, we may say m = (i − 1) → 0, where i is the most recent index such that s(i) = 0. We surmise that m = 257942 might appear after 2²⁴ terms. Hence, zeros are rare as n increases.

The most common term in s(1..n) = 1 for 9 ≤ n ≤ 10 and n ≥ 13, since 1 results from the setting of records, and is the root of trajectories m for all m outside of s(i−1).

There are two sources of m' in the sequence, of course, those novel m → s(m+1) = m', and those extant m ⇒ c(m) = m', where “→” represents Condition 0 and “⇒” Condition 1. Since the novel m must be records, we may restate Condition 1 as record m → s(m+1) = m', or even, the first instance of m → s(m+1) = m'. By the last statement it is clear that all terms in s are restated at least once as n increases.

Thus, there are 1s that result from new m and are thus reflections of s(m+1), and there are 1s that derive from extant m that report the total number of instances of m that have come before m in s. Since every m appears at least once in the sequence, and since the first appearance must be a record, the s(n) such that s(n) → 1 strictly increase as n increases; these are reflections of previous 1s. When s(n) = s(k) for k < n, we have s(n) ⇒ 1 for the second appearance of s(n).

We have 2 ⇒ c(2) → 1 for n ≥ 19, otherwise 1 ⇒ m ⇒ 1 for certain record m. So the second appearance of m is largely attributable to a preceding 2. ***

Subsequences t(i).

Since we have a single instance of Condition 0 followed by a number (ℓ−1) ≥ 1 of iterations of Condition 1, we can partition the sequence into subsequences t(i) = s(k…k+ℓ) according to condition. Such subsequences begin with a reflected term s(s(k−1)+1), followed by iterations of cardinalities m ⇒ c(m).

The first subsequences are:

 0 → 0 ⇒
 1 → 0 ⇒
 2 → 1 ⇒ 1 ⇒ 2 ⇒ 1 ⇒
 3 → 0 ⇒ 3 ⇒ 1 ⇒
 4 → 2 ⇒ 2 ⇒ 3 ⇒ 2 ⇒ 4 ⇒ 1 ⇒
 5 → 1 ⇒
 6 → 1 ⇒
 7 → 2 ⇒ 5 ⇒ 1 ⇒
 8 → 1 ⇒
 9 → 3 ⇒ 3 ⇒ 4 ⇒ 2 ⇒ 6 ⇒ 1 ⇒
10 → 0 ⇒ 4 ⇒ 3 ⇒ 5 ⇒ 2 ⇒ 7 ⇒ 1 ⇒
11 → 3 ⇒ 6 ⇒ 2 ⇒ 8 ⇒ 1 ⇒
...

Naturally the subsequence t(i) begins with m = (i − 1), a record R in s and therefore novel, triggering Condition 0. Thereafter, we have a number (ℓ−1) of iterations of Condition 1. For t(i) with i > 1, the first invocation of Condition 1 results in s(k) > s(k+1), since s(k) is a record and all previous s(n) < s(k) by definition. The subsequence t(i) proceeds with Condition 1 until it reaches 1. For t(i), c(1) = s(k), therefore, when we have obviously-existing s(k+ℓ) = 1, c(1) increments and sets a new record, ending t(i).

The subsequences t(i) for 1 ≤ i ≤ 3 are irregular. The subsequence t(1) = {0, 0} has nothing else to report but zeros, but since there are 2 zeros, m = 0 is the commonest entry and therefore its cardinality sets a record when called. Hence 0, not 1, terminates the subsequence. t(2) = {1, 0} again ends in 0, since there are more 0s in the sequence s than any other figure, and c(0) = 2 becomes the source of the record that kicks off t(3). Finally, t(3) = {2, 1, 1, 2, 1} enters three 1s into the sequence s, c(1) > c(0), therefore the record derives from c(1) = 3 that kicks off t(4). Zeros become rare as c(m) = 0 is not allowed; the sole source of zeros is therefore Condition 0 recalls, which become more rare as n increases. So for i > 3, all subsequences end in 1, and c(1) = (i − 1) commences the next subsequence.

We see that if m → s(m+1) = M, where M = 0 for n ≤ 4 else M = 1, then the subsequence terminates with ℓ = 2.

Figure 3.1 is a scatterplot of s(n) for 1 ≤ n ≤ 212, showing the subsequences in a color function i (mod 5). The labels are not s(n) but s(n−1) so as to illustrate the Condition 1 trajectories. The large colored dots indicate the fruits of Condition 0, i.e., record m → s(m+1), a recall value. The large black dots accentuate the first term in an occasion of a dithered repeated m.

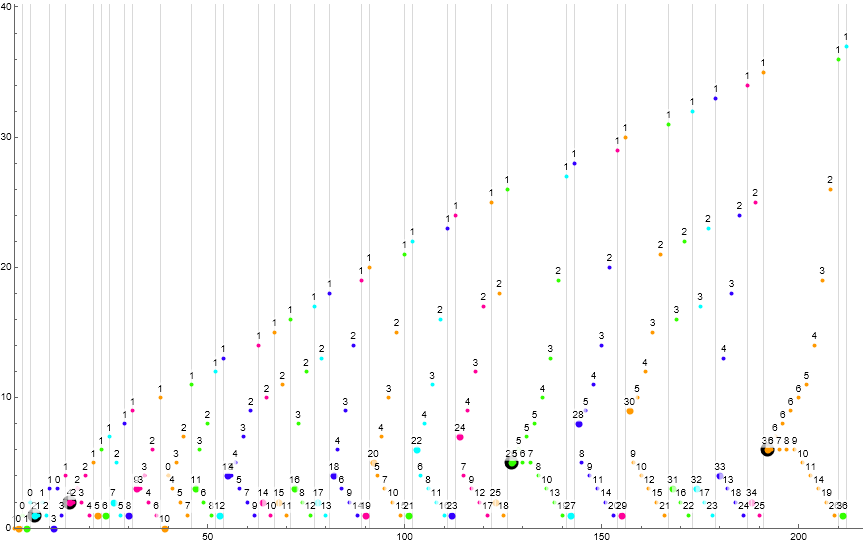
The scatterplot Figure 3.1, seen in the light of subsequences t(i), reveals 4 principal features of the sequence s.

1. Arrangement of s into subsequences t(i). The novel instigator s(k) → s(k+1) = s(s(k)+1) initiates a subsequence t(i) and places the recall-term s(k+1) < s(k) for k > 2. Thereafter, within the subsequence t(i) = s(k…k+ℓ), Condition 1 m ⇒ c(m) iterates recursively until we have s(k+ℓ) = 1 for i > 2.
2. Trajectories c(m). Since s(k+1) < s(k), the subsequent c(m) increment with the reiteration of small m. Hence we have the trajectories c(m) resulting from the recursion of Condition 1 in subsequence t(i). The trajectory of m = 0 manifests early and sets the first records, but since 0 is rare as it can only arise from reflection of earlier terms via Condition 0, the trajectory is not visually apparent in a scatterplot after c(0) = 4. The trajectories c(m) for m > 0 are plain to see as n increases. In a large scatterplot they take on a scalloped shape as n increases. Consider the j-th appearance of c(m) = v. the (j + 1)-th appearance of c(m) = v + 1. Therefore the commonest m sets records, and the union of s(1..k) where s(k) = c(m) represents the natural numbers [0 … c(m)].
3. Bisection of subsequences t(i) reveals a “preferential reverse indexing” of m at subsequence position s(k + ℓ − 2c(m) + 2). We find that m = 1 appears in t(i) at s(k + ℓ), meaning the last term of the subsequence for i > 2. Additionally, for sufficiently large i, we find m = 2 appears at s(k + ℓ − 2), i.e., the 3rd from last term in t(i), and m = 3 at s(k + ℓ − 4), 5th from last, etc. Hence, we have m ⇒ c(m) intercalated between these odd negative-indexed terms. This is responsible for the “butterflying” effect, where negatively-indexed even terms appear on the large end, and negatively-indexed odd terms appear on the small end of the range m (i.e., the y-axis in the scatterplot).
4. “Herringbone” numbers h. There is a pattern in certain subsequences t(i) wherein s(k+1) = s(k+2) = s(k+4) = … = s(k + 2r). This situation has c(s(k+1)) increment r times from s(k+1) = c(s(k+1)). We shall refer to such numbers as herringbone numbers h_i = c(h_i) in subsequence t(i) with repetition length r and instigator m → h_i.

Infinite restatement of m in s.

Condition 0 triggers the algorithm novel m → s(m + 1), a recall algorithm. Since the only novel m in s are its records R, the index (m + 1) increases as n increases, such that we have progressively later terms recalled into s. Furthermore, every term s(m) is reverberated later in the sequence through induction on account of R.

Therefore, for sequence s, we have the transformation of the sequence R_i → R = k₀ → N₀. Certainly, the indices of records map to records, therefore the indices of Condition 0, i.e., novel m, map to the nonnegative numbers. Ultimately, R_i → N₀.

A consequence of the inverse of this transformation is s(k) reappears at s(n+1) for n in R_i. We can reconstruct s using the terms s(n+1) for n in R_i. This is tantamount to s(n) = s(k+1) in t(n), that is, s(n) is reiterated in the second term of subsequence t(n).

Let us for the moment assume the recursion of Condition 1 between Condition 0 is finite, hence 1 < ℓ < ∞.

The reproduction of m = s(k) at s(n+1) for n in R_i implies that m > 0 will appear an infinite number of times in s on account of induction on R and the fact R_i > R. The case m = 0 cannot be generated by Condition 1, but on account of induction on R, 0 also repeats infinitely in s but much less frequently. The effect of Condition 1 merely places additional instances of m > 0 in s to be reverberated later in the sequence.

The sequence s would prove infinite since all terms are reflected at some later point following records that are the nonnegative integers. The reappearance of extant m = 1 ⇒ c(1) = R, which is 1 greater than the last record R and by definition new to s, recalling the next term in s.

If Condition 1 or ℓ is infinite after a certain k, then we will see no further records. However, Condition 1 involves the report of the cardinality c(m) of m in s. Therefore, suppose we have an infinite identical m in s. The report of m necessitates c(m) between instances, therefore adjacent m cannot be sustained. We would have m ⇒ m ⇒ m + 1. Ignoring this, at some point, c(m) > R and thereby triggers Condition 0, ending the run of Condition 1, a contradiction. Suppose we never repeat m in subsequence t(i). We know that 0 ≤ m ≤ R, therefore we know that such a prohibition entails 1 < ℓ ≤ R + 1, contradicting an infinite run of Condition 1. Finally, suppose that we may repeat any 0 ≤ m ≤ R infinitely. If we repeat any m in a finite range infinitely, we report the cardinality c(m), which obviously increments for each appearance of m, therefore some of the m in the run must be cardinalities of other m. However, at a certain point c(m) > R for some m, triggering Condition 0 and ending the run, a contradiction. Hence, Condition 1 cannot be repeated after Condition 0 in subsequence t(i) indefinitely, and ℓ is in fact finite.

Therefore s is infinite and contains an infinite number of copies of any distinct term s; the records R are the nonnegative integers. All m have trajectories in s, all cardinalities c(m) increase to infinity, and there are an infinite number of subsequences that begin with Condition 0 on account of the occasion of a final 1 in the previous subsequence for i > 2 (otherwise, a final 0), etc.

Trajectories of c(m).

The prominent striations that appear to emanate in an irregular way from origin are a manifestation of the trajectories of c(m) for m > 0, attributable to the predominant Condition 1 provenance of most of the terms in the sequence.

We speak of trajectories since we report m ⇒ c(m), and obviously for each new occasion of m in s, c(m) increments. If the reporting of a particular m ⇒ c(m) occurs frequently enough, to the eye, it seems to produce a stream in the scatterplot. Surely there is a trajectory for m = 0, but it reports so infrequently for large n that it doesn’t carry visual weight so as to read as a stream.

The cardinality of a particular m is not always reported into s; at times m enters s via Condition 0. This introduces imperfections in an otherwise orderly progression of any striation attributable to c(m). Indeed, m enters s through Condition 0 an infinite number of times, only much less frequently for small m than through Condition 1.

Since s is infinite and contains infinite copies of m in the nonnegative integers, we may trace the cardinality of any 0 ≤ m < R in s(1..n) as n increases.

Figure 5.1 is a scatterplot of s(n) for 1 ≤ n ≤ 2⁸, labeling s(n) instead with s(n−1) = m, the progenitor of s(n). We apply a color function m (mod 8) to represent the fruits of Condition 1 m ⇒ c(m) with small dots. The fruits of Condition 0, m → s(m + 1) appear in large black dots, rehashing s in order of appearance and delimit the subsequences t(i). Evident in the scatterplot are the trajectories of 1 through 5, with larger m less visually apparent at this range.

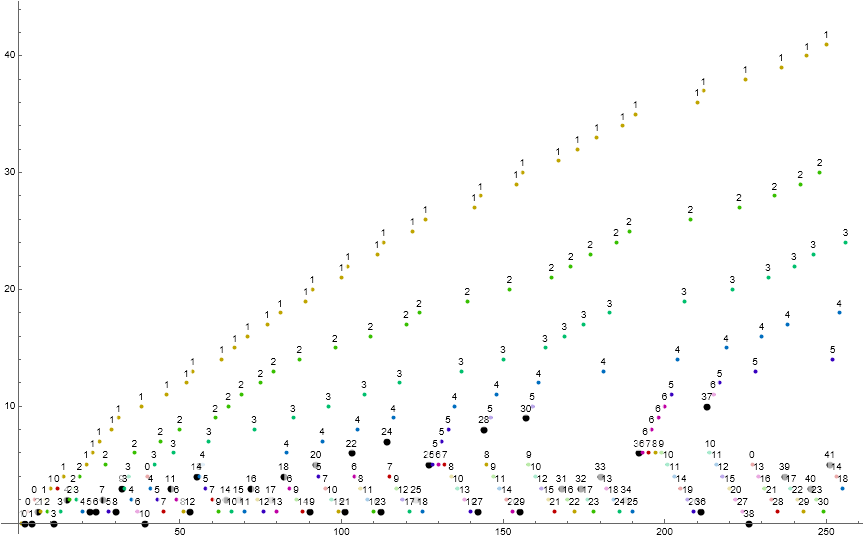
We should expect the crossing of trajectories as the cardinality of c(m) overtakes c(m') for m ≠ m'. Indeed this happens for m = 1 and m' = 0 in the first dozen terms. The large scale scatterplot seems to suggest that the trajectories do not cross, hence, the cardinality c(m) > c(m') for 1 < m < m'. What makes the trajectories for m > 0 stay in their lanes?

The records R in s increment as n increases, albeit in an irregular, discontinuous fashion. This suggests that the numbers m in s are introduced in order. A second appearance through either condition certainly happens by definition after the first, hence c(1) ≥ c(2). We know that c(1) exceeds c(0) since the latter cannot be generated by Condition 1, the dominant condition in the sequence, hence the number of zeros in s is relatively few compared to the number of 1s. Hence the trajectories must roughly remain in their lanes, but certainly so as n increases.

Herringbone numbers h.

In fact, the situation of greater cardinality for smaller m > 0 intensifies as n increases.

Suppose we begin a subsequence t(i), i > 2, with s(k) = (i − 1) such that s(k+1) = s(i) = m = 1. We have s(k+1) = 1 ⇒ c_i(1) > c_(i−1)(1), and thus a record in s(k+2), hence novel s(k+2) and the subsequence ends when it yields s(c_i(1)+1) = s(i + 1) via Condition 0. We know that 1 terminates the subsequence t(i) because it is commonest for i > 2, and thus its cardinality sets a record (by definition).

Now suppose that we have s(k+1) = s(i) = m “low”. Since m is small, it is more common and a “high” number c(m) will follow. But this “high” m is not common so it is followed by a low c(m). The low and high numbers may alternate.

Alternating low and high numbers eventually set a record when the low m = 1, triggering Condition 0 and ending the subsequence t(i).

Suppose that we have s(k+1) = s(i) = h such that c(h) = h. Then we have h ⇒ h ⇒ (h+1), that is, 2 consecutive identical terms h. From this point, perhaps since (h+1) > h, c(h+1) < h, and hence we have alternating low and high numbers. It is also likely that we might have h ⇒ h ⇒ (h+1) ⇒ h ⇒ (h+2), etc. At a certain point, the intervening high m will trigger interleaved progressively lower m until m = 1.

Figure 6.1 is a scatterplot of s(n) for 1 ≤ n ≤ 360, with a color function that highlights subsequence i (mod 3). The large black circles show the instance of a pattern {h, h}, i.e., repeated terms h.

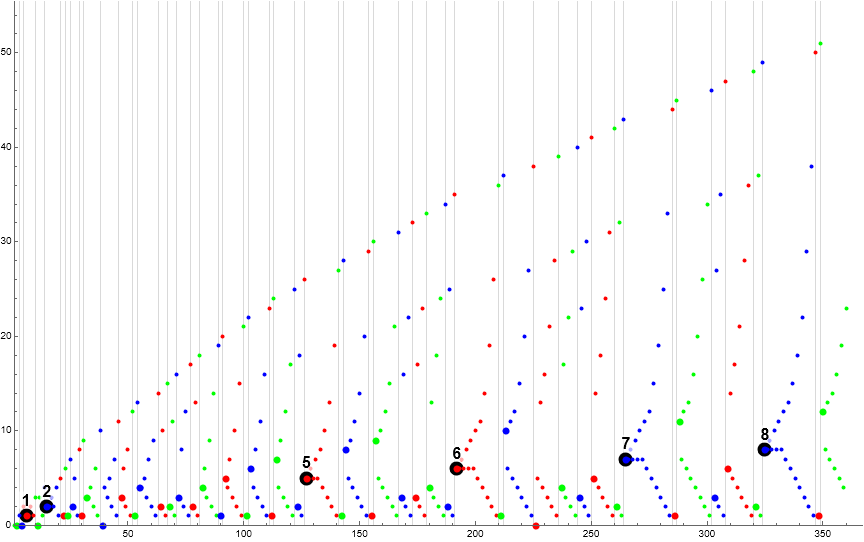
Indeed we can find instances of duplicated h in s. The first appears in t(2) = {2, 1, 1, 2, 1}, where we have L = 2 reiterations of s(k+1) = 1 following the first.

Table 6.1 is a list of the first 8 cases of duplicated h. The term h = s(k+1). Table A describing the smallest 188 cases of duplicated h in s(n) for 1 ≤ n ≤ 2¹⁸ appears in the appendix.

 i     k   L   c(i) = s(k..(k+l−1))
-----------------------------------
 1     1   2   {0, 0}
 3     5   3   {2, 1, 1, 2, 1}
 5    14   3   {4, 2, 2, 3, 2,  4, 1}
10    31   2   {9, 3, 3, 4, 2,  6, 1}
14    54   2  {13, 4, 4, 5, 3,  7, 2,  9, 1}
27   126   4  {26, 5, 5, 6, 5,  7, 5,  8, 4, 10, 3, 13, 2, 19, 1}
36   191   5  {35, 6, 6, 7, 6,  8, 6,  9, 6, 10, 5, 11, 4, 14, 3, 19, 2, 26, 1}
44   264   5  {43, 7, 7, 8, 7,  9, 7, 10, 7, 11, 6, 12, 5, 15, 4, 19, 3, 25, 2, 33, 1}
50   324   5  {49, 8, 8, 9, 8, 10, 8, 11, 8, 12, 7, 13, 6, 15, 5, 18, 4, 22, 3, 29, 2, 38, 1}
...

The longest L = 41 for 1 ≤ n ≤ 2¹⁸, starting with s(257118) = 3632 followed by h = 186.

An example of a subsequence with repeating h is t(65):

64 ⇒ 10 ⇒ 10 ⇒ 11 ⇒ 10 ⇒ 12 ⇒ 10 ⇒ 13 ⇒ 10 ⇒ 14 ⇒ 10 ⇒ 15 ⇒ 9 ⇒ 16 ⇒
8 ⇒ 17 ⇒ 7 ⇒ 19 ⇒ 6 ⇒ 21 ⇒ 5 ⇒ 25 ⇒ 4 ⇒ 31 ⇒ 3 ⇒ 39 ⇒ 2 ⇒ 50 ⇒ 1 →

In this subsequence h = 10 is repeated L = 5 times after s(k+1). What we see is that there is a range {h…(h+L−1)} where m in this range has identical cardinalities. The action of such a subsequence is to build a “cliff” c(h) and a “plain” c(m) for m in {(h+1)…(h+L−1)}. Observations show that L is nondecreasing as k increases.

We may take a snapshot of the values of cardinalities c(m) for 0 ≤ m ≤ R at k. For t(65) = s(487..515) = {64, 10, 10, 11, 10, …, 1}, we list such cardinalities:

6, 65, 50, 39, 31, 25, 21, 19, 17, 16, 10, 10, 10, 10, 10, 9, 8, 7, 7, 6, 6, 5, 5, 5, 5, 4, 4, 4, 4, 4, 4, 3, 3, 3, 3, 3, 3, 3, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1

Ignoring c(0) = 6, the cardinalities generally grade down as m increases, however we see c(10..14) = 10. The cardinalities feature a “gutter” that includes the “cliff” c(9) = 16 followed by the “plain” c(10..14) = 10.

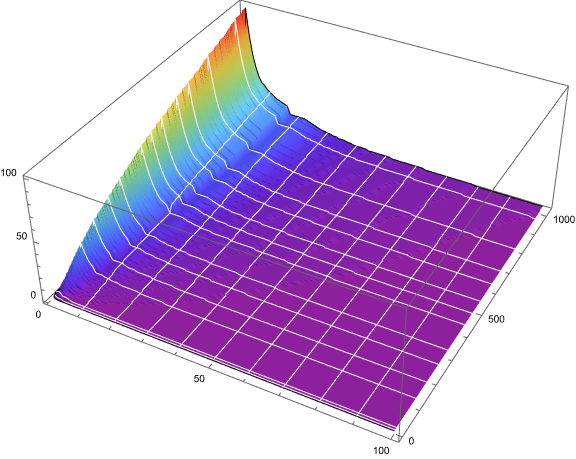
Figure 6.2 is a 3-dimensional plot of s(n) for 1 ≤ n ≤ 2¹⁰, on the y-axis at right, 0 ≤ m ≤ 100 on the x-axis at bottom, and the color function and height representing c(m) at left. The white gridlines that move left to right “down” the slope correspond to s(k) that start t(i) with duplicated h; t(65) appears just below the label 500 on the right (y) axis. The “gutter” is a prominent feature of the snapshots of the range of cardinalities.

Bisection of subsequences t(i).

We can examine other patterns in the series of subsequences, among terms justified in reverse to the end of the subsequence. When we see the patterns laid out in this way, many things make sense about the scatterplot. We shall use a reverse index j that counts down from (k+ℓ−1) toward k.

Let subsequence bisection a₁ include terms s(k+ℓ−j) in subsequence t(i) with odd 1 ≤ j ≤ ℓ and let subsequence bisection a₂ have even j. We note that s(k+0) = (i − 1), s(k+1) = s(i), s(k+2) = c(s(i)), etc., and for i > 2, s(k+ℓ−1) = 1.

The terms a₁(j/2) begin with 1 and usually increase to 2, 3, 4, etc., while the terms a₂((j−1)/2) are much larger, falling from a record a₂(0) = s(k) that is the first term of the subsequence t(i+1). As j increases, a₁ and a₂ approach one another. The pattern is plainer to see in the table below.

Table 7.1. A list of terms in subsequence t(i) presented in reverse, starting with term j = 1, meaning s(k+ℓ−1), the last term which is 1 for i > 2, and proceeding backward toward term j = ℓ, meaning s(k) = (i − 1), the first term. The penultimate term j = (ℓ− 1) in the reversed subsequence, s(k+1) = s(i). We bold terms in the odd bisection a₁ (which are on the “low” end) and those in the even bisection a₂ (which are figures on the “high” end). We place in parentheses repeated h, and the record R = (i − 1) that starts the subsequence t(i).

 i  1   2  3   4  5   6  7
--------------------------
 1 (0) (0)
 2  0  [1]
 3  1   2 (1) (1)[2]
 4  1   3  0  [3]
 5  1   4 (2)  3 (2) (2)[4]
 6  1  [5]
 7  1  [6]
 8  1   5  2  [7]
 9  1  [8]
10  1   6  2   4 (3) (3)[9]
11  1   7  2   5  3   4  0 [10]
12  1   8  2   6  3 [11]
13  1 [12]
14  1   9  2   7  3   5 (4) (4) [13]
15  1  10  2 [14]
16  1  11  2 [15]
17  1  12  2   8  3 [16]
18  1  13  2 [17]
19  1  14  2   9  3   6  4 [18]
20  1 [19]
21  1  15  2  10  3   7  4   5 [20]
22  1 [21]
23  1  16  2  11  3   8  4   6 [22]
24  1 [23]
25  1  17  2  12  3   9  4   7 [24]
26  1  18  2 [25]
27  1  19  2  13  3  10  4   8  (5)  7  (5)  6  (5) (5) [26]
28  1 [27]
29  1  20  2  14  3  11  4   9   5   8 [28]
30  1 [29]
31  1  21  2  15  3  12  4  10   5   9 [30]
32  1  22  2  16  3 [31]
33  1  23  2  17  3 [32]
34  1  24  2  18  3  13  4 [33]
35  1  25  2 [34]
36  1  26  2  19  3  14  4  11   5  10  (6)  9  (6)  8  (6)  7  (6) (6)[35]
----------------------------------------------------------------------------
 i  1   2  3   4  5   6  7   8   9  10  11  12  13  14  15  16  17  18  19

Let us ignore the bracketed record and focus on subsequences i > 2, since there are nonconformities associated with the replacement of 0 by 1 as commonest term in s.

Firstly, we see that a₁ contains m in order as j increases, but that m must be introduced by repetition as h. Furthermore, the increasing, ordered portion of a₁ lengthens by 1 whenever h appears.

Secondly, we see that if s(i) = 1 for i > 3, then we have the shortest possible subsequence t(i) with length ℓ = 2. Plainly, R → 1 ⇒ R', thus the subsequence ends. There is a relationship of the magnitude of s(i) (for sufficiently large i) and ℓ, but locally longest subsequences pertain to those with h.

Thirdly, quite naturally, for the ordered portion of a₁ that features incrementing m, we have cardinalities that follow (which pertain to the following term!) that increment as i increments, certainly so long as the following m is not preempted by low s(i).

It seems that any given m appears such that c(m) = m hence we have repeated m = h. This would imply that m appears m times by the time we have repeated h. This makes sense since such repetition as {h, h} cannot otherwise occur. We observe that there are occasions of m with c(m) = (m − 1) in preceding subsequences that have the progression out of focus and the bisections immediately diverge.

Therefore we have R → s(i) that happens to resonate with a range of m that have identical c(m); the c(m) increase as n increases, but more markedly for small m, and each m see duplication as {h, h}. The situation propagates as n increases, with L nondecreasing as h increases. If it weren’t for the duplication of h, we would see the latest R in a run of intercalated records set a record for ℓ.

We can employ h as the index of an occasion of duplicated h in subsequence t(J). Outside of t(J), for J < i < J', the longest possible subsequence t(i) has length ℓ = 2h.

In a strange way, given s(k+ℓ−j) with j odd, after m having been duplicated, s(k+ℓ−(j+1)) functions as the cardinality of s(k+ℓ−j) in s that haven’t followed R. Suppose we have h ⇒ c(h) = h at subsequence t(i), i.e., duplicated h. If we have K subsequences between the h-th occasion and the (h+1)-th occasion of duplicated h that have the maximum ℓ = 2h, then when h' = (h+1) arises, we find that the “reverse cardinality” of h = h + K, and hence L' = K + 3.

The development of the “cliff” and “plain” that creates a “gutter” among the cardinalities at n seems to arise when we have h appear. The multiple copies of h send that m into a cliff (markedly increasing cardinality) and broaden the plain of identical cardinalities.

The occasion of {h, h} delimits the “upper end” of a sail shape in the scatterplot, where the bisections of the subsequences converge until the next herringbone number h' = (h+1) duplicates in s. Therefore the action of cardinalities and the arising of herringbone numbers h in their turn produce the characteristic “sailboat” shape of voids in the scatterplot.

Summary.

1. The sequence s is infinite; all nonnegative integers m are repeated infinitely.
   1. Since m = 0 cannot result from Condition 1, it is repeated much less often.
   2. The cardinalities of m > 0 grade from 1 down to h in a “hyperbolic” manner, then from h down to R in a gentle manner. The cardinality of 1 in s is greatest for n > 13.
2. Records are the nonnegative integers. Let R < R' be adjacent records: R' = R + 1 for all R, since records R > 0 are the result of Condition 1, a cardinality function. The only novel m in the sequence are its records.
3. The minima consist of 0 ≤ m ≤ 1. Since 0 cannot be generated by Condition 1, the only zeros in s are reflections of s(1) via Condition 0. Therefore, the cardinality of 1 surpasses that of 0 and 1 is the commonest M in s for n ≥ 12.
4. The appearance of the commonest term M instigates a record in s: 1 ⇒ c(1) = R for n >
5. Occasions of the Condition 0 algorithm m → s(m+1) report all terms m in s in order, later in the sequence. Hence all terms m are restated in s. Since the restatements or reflections of m = s(k) appear at s(n) for n > k, there are infinite reflections of m in s.
6. The sequence s can be divided into finite subsequences t(i) with at least 1 instance of Condition 1 follows Condition 0.
   1. Subsequences begin with s(k) = (i − 1) and end with the commonest m in s, which for i ≤ 2 is m = 0, and for all other i, is m = 1.
   2. The Condition 1 recursion in the coda of the subsequence proceeds from some value m toward 1 and toward a record in a manner that intercalates terms in these bifurcated processes. Hence the run of Condition 1 is finite and the subsequence t(i) has length 2 ≤ ℓ < ∞. As a consequence, there are infinite occasions of Condition 0 through the reporting of c(M) = R, and infinite records that recreate the sequence of nonnegative integers.
   3. If s(i) = 1, ℓ_i = 2.
7. The scatterplot exhibits trajectories associated with m ⇒ c(m) such that m > 0 have cardinalities that are nonincreasing as m increases toward the record r. Therefore the scatterplot has trajectories that do not cross except for that of m = 0.
8. Let a₁ be terms s(k+ℓ−j) in subsequence t(i) with odd 1 ≤ j ≤ ℓ and let a₂ have even j. We note that s(k+0) = (i − 1), s(k+1) = s(i), s(k+2) = c(s(i)), etc., and for i > 2, s(k+ℓ−1) = 1. The terms a₁(j/2) begin with 1 and usually increase to 2, 3, 4, etc., while the terms a₂((j−1)/2) are much larger, falling from a record a₂(0) = s(k) that is the first term of the subsequence t(i+1). As j increases, a₁ and a₂ approach one another.
9. There are cases of duplicated terms h. In this case, we have the subsequence R → s(R+1) ⇒ h ⇒ h ⇒ (h + 1) ⇒ … with L copies of h. This pattern has h nondecreasing as i increases, but h ≠ 2 and h ≠ 3, and L nondecreasing at a slower rate. The term h can be repeated only twice adjacently. This is the extreme case of No. 8 above.
10. The “sailboat” sequence is so-named for the conspicuous voids that open up at a particular subsequence t(i) then gradually narrow as i increases to a subsequence that has duplicated h. The voids affect the trajectories, causing them to increase and moderate to produce a “scallop” over each sailboat.

This concludes our examination.

Appendix:

Table A1: List of the occasions of repeated h in s(n) for 1 ≤ n ≤ 2¹⁸. This duplicated h is found in subsequence t(i). The first term s(k) = (i − 1) is followed by s(k+1) = s(k+2) = h. We have h = s(h + 2x) for 1 ≤ x ≤ (L − 1). There are L copies of h in subsequence c(i).

     k  (i-1)   h   L
---------------------
     1     0    0   2
     5     2    1   3
    14     4    2   3
    31     9    3   2
    54    13    4   2
   126    26    5   4
   191    35    6   5
   264    43    7   5
   324    49    8   5
   435    60    9   6
   487    64   10   6
   543    68   11   6
   625    74   12   6
   689    78   13   6
   801    86   14   6
   962    97   15   7
  1137   108   16   8
  1326   119   17   9
  1416   123   18   9
  1652   138   19   9
  1899   151   20  10
  2162   164   21  11
  2310   170   22  11
  2464   176   23  11
  2658   184   24  11
  2780   188   25  11
  3146   207   26  11
  3503   222   27  12
  3776   233   28  12
  4008   241   29  12
  4204   247   30  12
  4488   257   31  12
  4640   261   32  12
  5120   282   33  12
  5595   299   34  13
  5821   305   35  13
  6187   317   36  13
  6361   321   37  13
  6947   344   38  13
  7528   363   39  14
  8131   382   40  15
  8453   390   41  15
  8783   398   42  15
  9173   408   43  15
  9455   414   44  15
  9955   428   45  15
 10169   432   46  15
 10961   459   47  15
 11714   480   48  16
 11942   484   49  16
 12844   513   50  16
 13699   536   51  17
 13941   540   52  17
 14961   571   53  17
 15926   596   54  18
 16274   602   55  18
 16954   618   56  18
 17218   622   57  18
 18386   655   58  18
 19495   682   59  19
 19773   686   60  19
 21075   721   61  19
 22310   750   62  20
 22794   758   63  20
 23436   770   64  20
 23844   776   65  20
 24708   794   66  20
 25016   798   67  20
 26504   835   68  20
 27925   866   69  21
 29380   897   70  22
 30014   907   71  22
 30568   915   72  22
 31380   929   73  22
 31844   935   74  22
 32898   955   75  22
 33246   959   76  22
 35044  1000   77  22
 36711  1033   78  23
 38414  1066   79  24
 39222  1078   80  24
 39846  1086   81  24
 40846  1102   82  24
 41366  1108   83  24
 42628  1130   84  24
 43016  1134   85  24
 45152  1179   86  24
 47083  1214   87  25
 49052  1249   88  26
 50052  1263   89  26
 50746  1271   90  26
 51952  1289   91  26
 52528  1295   92  26
 54016  1319   93  26
 54444  1323   94  26
 56946  1372   95  26
 59159  1409   96  27
 59601  1413   97  27
 62295  1464   98  27
 64680  1503   99  28
 65574  1513  100  28
 66478  1523  101  28
 67510  1535  102  28
 68434  1545  103  28
 69600  1559  104  28
 70544  1569  105  28
 71840  1585  106  28
 72664  1593  107  28
 74184  1613  108  28
 74862  1619  109  28
 76690  1645  110  28
 77190  1649  111  28
 80226  1702  112  28
 82955  1743  113  29
 85728  1784  114  30
 87142  1800  115  30
 88188  1810  116  30
 89740  1828  117  30
 90650  1836  118  30
 92440  1858  119  30
 93186  1864  120  30
 95304  1892  121  30
 95852  1896  122  30
 99342  1953  123  30
102427  1996  124  31
105558  2039  125  32
107240  2057  126  32
108388  2067  127  32
110216  2087  128  32
111212  2095  129  32
113292  2119  130  32
114106  2125  131  32
116534  2155  132  32
117130  2159  133  32
121104  2220  134  32
124565  2265  135  33
125409  2271  136  33
128047  2303  137  33
128665  2307  138  33
132913  2370  139  33
136624  2417  140  34
137498  2423  141  34
140356  2457  142  34
140996  2461  143  34
145528  2526  144  34
149499  2575  145  35
150619  2583  146  35
153109  2609  147  35
154025  2615  148  35
157147  2651  149  35
157817  2655  150  35
162677  2722  151  35
166956  2773  152  36
167640  2777  153  36
172760  2846  154  36
177271  2899  155  37
178853  2911  156  37
180447  2923  157  37
182229  2937  158  37
183847  2949  159  37
185823  2965  160  37
187465  2977  161  37
189629  2995  162  37
191295  3007  163  37
193641  3027  164  37
195129  3037  165  37
197651  3059  166  37
198933  3067  167  37
201899  3095  168  37
202941  3101  169  37
206581  3139  170  37
207339  3143  171  37
212967  3214  172  37
217988  3269  173  38
223067  3324  174  39
225585  3344  175  39
227391  3356  176  39
230099  3378  177  39
231709  3388  178  39
234601  3412  179  39
235985  3420  180  39
239341  3450  181  39
240463  3456  182  39
244525  3496  183  39
245339  3500  184  39
251599  3575  185  39
257118  3632  186  40
259053  3645  187  40
...

Code 1: Generate a(n):

Block[{a = {0}, c, s = {}},
  Do[If[IntegerQ@ c[#],
    AppendTo[a, c[#]]; c[#]++; Set[s, Rest@ s],
    AppendTo[a, a[[# + 1]]]; Set[c[#], 1]] &@ a[[-1]];
    Set[s, Insert[s, a[[-2]], LengthWhile[s, # < a[[-2]] &] + 1]], 120]; a]

Document Revision Record.

2021 0703 1000 Draft.