Recordbearing Inventory Sequence.
OEIS A348328, a sequence of David Sycamore, Mevagissey, England.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 1011.
Introduction.
We consider an inventory sequence one beginning with a seed (usually 0) that reports cardinality c(m) of numbers m that appear in the sequence in turn following a reset triggered by the report of a zero. The turns involve reporting the number of 0s, then 1s, then 2s, etc. until we write a 0, wherein we return to reporting the number of 0s once again. Because of this, we may partition the sequence into segments or cycles delimited by occasions of 0. If the sequence starts with seed 0, then this should be deemed the zeroth or first such cycle. Subsequent cycles include a number of nonzero terms ending with a zero. Thus we might see the sequence an irregular triangle T(n,k), where n represents the cycle number, and k an index in the cycle that governs the reports of cardinalities c(k).
It is clear that the register c(m) may increment even when it hasn’t reported, and that the scatterplot will exhibit a series of trajectories associated with the registers c(m). Every alteration of the registers is not visible, since increment may occur after a report in a given cycle. We expect the cycle length ℓ to be nondecreasing.
The inventory sequence as such stands to be a pure sequence of counting and millions of terms can be calculated in short order, resulting in a scatterplot characterized by nondecreasing periodicity and trajectory.
Joseph Rozhenko wrote the original inventory sequence OEIS A342585. This sequence merely counts m and reports c(m) in turn, i.e., c(0), c(1), c(2), etc. until we encounter a null register; it is the simplest version of the inventory sequence as such and is a fast computation study. This sequence begins as follows:
0, 1, 1, 0, 2, 2, 2, 0, 3, 2, 4, 1, 1, 0, 4, 4, 4, 1, 4, 0, 5, 5, 4, 1, 6, 2, 1, 0, 6, 7, 5, 1, 6, 3, 3, 1, 0, 7, 9, 5, 3, 6, 4, 4, 2, 0, 8, 9, 6, 4, 9, 4, 5, 2, 1, 3, 0, 9, 10, 7, 5, 10, 6, 6, 3, 1, 4, 2, 0, 10, 11, 8, 6, 11, 6, 9, 3, 2, 5, 3, 2, 0, 11, 11, 10, ...
Dr. Neil Sloane included this sequence among several highlighted 28 August 2021; after which many auxiliary sequences and variants issued forth. Certain variants included a sort of payload function through which we examine the terms. The payload function normally reports directly following a reset. Some variants admit an intermediate zero so as to fully report all nonzero registers.
We consider a variant A348328 = a such that we start with a(0) = 0, thereafter, after the appearance of a zero, we report the number of records in the sequence, then we report the number of 0s, 1s, etc. until we report a null register (i.e., a 0), and we recommence with reporting the number of records, the number of 0s, the number of 1s, etc. In terms of computation, we assign the register c(−1) to records.
The sequence a begins as follows:
0, 1, 1, 2, 1, 0, 3, 2, 3, 2, 2, 0, 4, 3, 3, 4, 4, 3, 0, 5, 4, 3, 4, 6, 5, 2, 1, 0, 7, 5, 4, 5, 6, 6, 4, 3, 1, 0, 8, 6, 5, 5, 7, 7, 6, 5, 3, 1, 0, 9, 7, 6, 5, 8, 7, 8, 6, 5, 3, 1, 0, 10, 8, 7, 5, 9, 7, 10, 7, 8, 5, 2, 2, 0, 11, 9, 7, 7, 9, 7, 11, 7, 12, 5, 4, 2, 2, 1, 0, 13, 10, 8, 9, 9, 8, 12, 7, 13, 7, 6, 3, 2, 2, 2, 0, 14, 11, 8, 12, 10, 8, 12, 8, 14, 10, 6, 5, 3, 4, 2, 2, 0, ...
This sequence can be generated by Code 1. We have generated 212 cycles = 15018495 terms, but have also analyzed 10000 cycles (174926478 terms).
Table 1 lists terms −1 ≤ k in cycles 0 ≤ n ≤ 10:
n r 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
--------------------------------------------------------
0: 0
1: 1 1 2 1 0
2: 3 2 3 2 2 0
3: 4 3 3 4 4 3 0
4: 5 4 3 4 6 5 2 1 0
5: 7 5 4 5 6 6 4 3 1 0
6: 8 6 5 5 7 7 6 5 3 1 0
7: 9 7 6 5 8 7 8 6 5 3 1 0
8: 10 8 7 5 9 7 10 7 8 5 2 2 0
9: 11 9 7 7 9 7 11 7 12 5 4 2 2 1 0
10: 13 10 8 9 9 8 12 7 13 7 6 3 2 2 2 0
...
Table 2 lists the number of m in row 0 ≤ n ≤ 10 of a, writing “.” for zero for clarity. Hence, for n = 2, there is 1 zero, no 1s, three 2s, and two 3s.
n: 0 1 2 3 4 5 6 7 8 9 10 11 12 13
----------------------------------------------
0: 1
1: 1 3 1
2: 1 . 3 2
3: 1 . . 3 3
4: 1 1 1 1 2 2 1
5: 1 1 . 1 2 2 2 1
6: 1 1 . 1 . 3 2 2 1
7: 1 1 . 1 . 2 2 2 2 1
8: 1 . 2 . . 2 . 3 2 1 2
9: 1 1 2 . 1 1 . 4 . 2 . 2 1
10: 1 . 3 1 . . 1 2 2 2 1 . 1 2
...
The records r include the following:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 31, 32, 33, 34, 37, 38, 39, 43, 44, 45, 46, 47, 49, 52, 53, 55, 58, 61, 62, 63, 67, 70, 71, 73, 76, 78, 81, 84, 87, 89, 91, 94, 95, 104, 113, 121, 129, 135, 142, 147, 151, 155, 164, 171, 177, 185, 192, 198, 204, 211, 218, 226, 231, 237, 242, 248, 255, 261, 264, 268, 270, 272, 275, 278, 283, 284, 294, 303, 312, 317, 324, 331, 339, 349, 357, 367, 374, 381, 382, 396, 409, 423, 435, 448, 460, 470, 478, 484, 492, 497, ...
Given 10000 cycles, there are 10092 records. The records appear on average 1 to a cycle, however there are cycles that never set records (assuming the zeroth cycle constitutes a(0) = 0, these are cycles 27, 38, and 46; are there any others?), and there are cycles that feature 2 records:
1, 4, 9, 24, 25, 68, 91, 102, 103, 138, 139, 259, 260, 287, 288, 289, 326, 327, 328, 329, 330, 331, 332, 368, 378, 379, 380, 646, 647, 648, 649, 868, 869, 1216, 1217, 1218, 1219, 1220, 1221, 1222, 1558, 1559, 1560, 1561, 2951, 2952, 2953, 2954, 3207, 3208, 3209, 3210, 3211, 3970, 3971, 3972, 3973, 3974, 3975, 3976, 3977, 3978, 3979, 3980, 6576, 6577, 6578, 6579, 6580, 7136, 7137, 7138, 7139, 7140, 7141, 7142, 7143, 7144, 7145, 7146, 7147, 9640, 9641, 9642, 9643, 9644, 9645, 9646, 9647, 9648, 9649, 9650, 9651, 9652, ...
Seeing as many of these indices occur in runs, we might abbreviate thus:
1, 4, 9, 24..25, 68, 91, 102..103, 138..139, 259..260, 287..289, 326..332, 368, 378..380, 646..649, 868..869, 1216..1222, 1558..1561, 2951..2954, 3207..3211, 3970..3980, 6576..6580, 7136..7147, 9640..9652, ...
Are there any cycles that set 3 records?
Furthermore, records tend to be set in the first term for the first thirty or so cycles, but as n increases, the records occur at the k-th term in a cycle for k > 4.
Figure 1: Scatterplot of a(n) ≤ 405 for 1 ≤ n ≤ 216, showing a tangle of detail in the densest part of the plot.
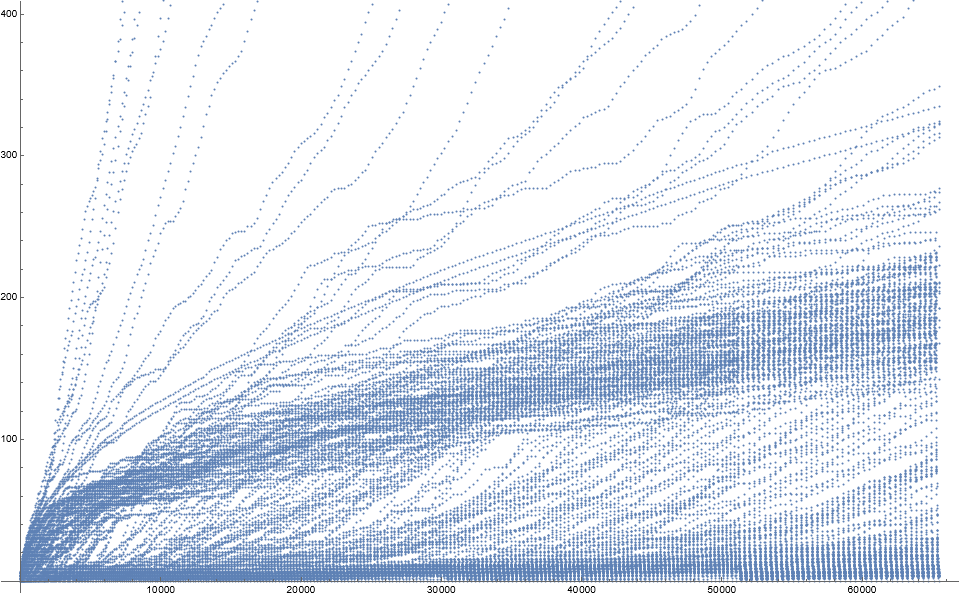
The scatterplot of course exhibits trajectories associated with the reporting of c(m) at most once per cycle. The two purer curves correspond to c(r) (the cardinality of records) and c(0), respectively.
Figure 2: Scatterplot of a(n) for 1 ≤ n ≤ 43058, showing 256 cycles. The colors pertain to certain trajectories. Black = c(r), red = c(0), orange = c(1), yellow = c(2), green = c(3), cyan = c(4), blue = c(5), purple = c(6).
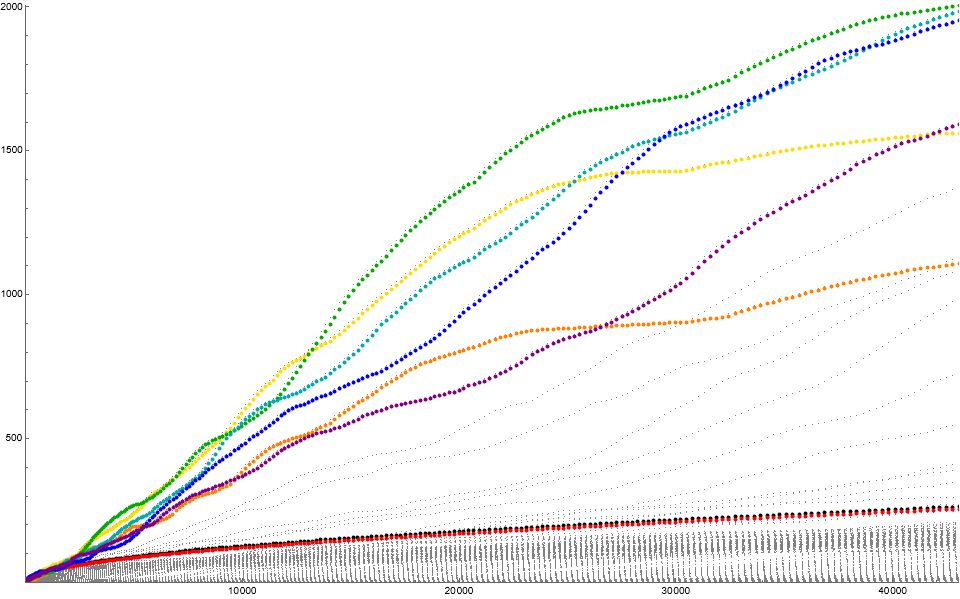
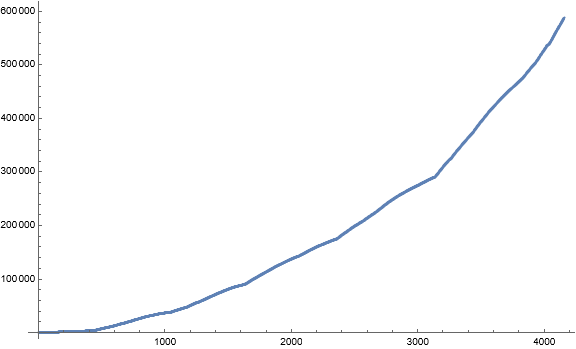
Figure 3: Scatterplot of records r(i) for 1 ≤ i ≤ 4158.
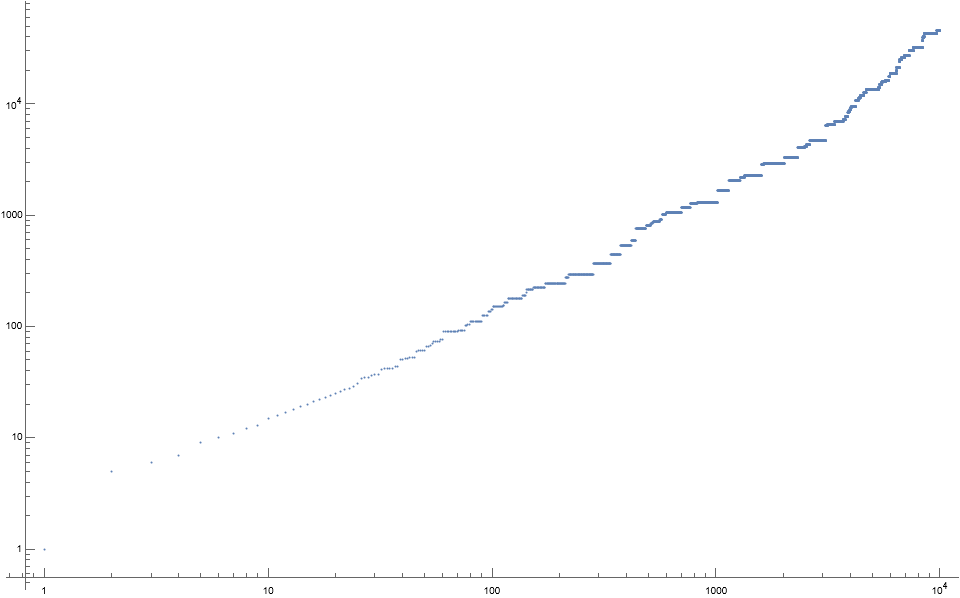
We may derive row lengths ℓ and sums s. Sequence ℓ begins as follows:
1, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 31, 34, 35, 35, 36, 37, 37, 41, 42, 42, 42, 42, 44, 44, 50, 50, 52, 52, 53, 53, 53, 59, 61, 61, 61, 61, 66, 66, 68, 70, 74, 74, 74, 74, 76, 76, 90, 90, 90, 90, 90, 90, 90, 90, 90, 90, 92, 92, 92, 92, 92, 103, 103, 105, 105, 111, 111, 111, 111, 111, 111, 111, 111, 111, 111, 111, 126, 126, 126, 126, 126, 136, 136, 136, 142, 142, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 150, 154, 154, 163, 163, 163, 163, 180, 180, 180, ...
This leads to a sequence z of indices of 0 in a via z = −1 + partial sums of ℓ:
0, 5, 11, 18, 27, 37, 48, 60, 73, 88, 104, 121, 139, 158, 178, 199, 221, 244, 268, 293, 319, 346, 374, 403, 434, 468, 503, 538, 574, 611, 648, 689, 731, 773, 815, 857, 901, 945, 995, 1045, 1097, 1149, 1202, 1255, 1308, 1367, 1428, 1489, 1550, 1611, 1677, 1743, 1811, 1881, 1955, 2029, 2103, 2177, 2253, 2329, 2419, 2509, 2599, 2689, 2779, 2869, 2959, 3049, 3139, 3229, 3321, 3413, 3505, 3597, 3689, 3792, 3895, 4000, 4105, 4216, 4327, 4438, 4549, 4660, 4771, 4882, 4993, 5104, ...
Figure 4: Log-log scatterplot of ℓ(n) for 0 ≤ n ≤ 10000:
The row sums s begin as follows:
0, 5, 12, 21, 30, 41, 53, 65, 80, 94, 111, 129, 147, 167, 187, 209, 232, 256, 280, 305, 331, 358, 386, 418, 448, 482, 518, 554, 589, 626, 664, 705, 747, 789, 831, 872, 916, 960, 1011, 1060, 1111, 1163, 1216, 1268, 1321, 1380, 1442, 1502, 1563, 1625, 1690, 1755, 1820, 1890, 1963, 2037, 2107, 2178, 2250, 2322, 2417, 2504, 2591, 2677, 2766, 2853, 2939, 3024, 3109, 3196, 3283, 3369, 3456, 3542, 3628, 3738, 3837, 3939, 4039, 4148, 4254, 4361, 4466, 4571, 4677, 4783, 4888, 4993, 5099, 5205, 5348, 5469, 5590, 5710, 5830, 5970, 6100, 6230, 6372, 6511, 6658, 6802, 6946, 7091, 7235, 7379, 7524, 7668, 7811, 7954, 8098, 8247, 8395, 8557, 8717, 8874, 9031, 9211, 9384, 9557, ...
This concludes our examination.
Appendix:
Block[{c, k, m, r = 0},
c[-1] = 1; c[0] = 1;
{0}~Join~Reap[Monitor[Do[k = -1;
While[IntegerQ[c[k]], Set[m, c[k]]; Sow[m];
If[IntegerQ@ c[m], c[m]++, c[m] = 1];
If[m > r, r = m; c[-1]++]; k++];
Sow[0]; c[0]++, {i, 2^8}], i]][[-1, -1]]]
Concerns OEIS sequences:
A342585: The inventory sequence.
A343880: Indices of 0 in A342585.
A347299: Row lengths of A342585.
A347315: Row sums of A342585.
A347316:
Irregular triangle read by rows: T(n,k) = number of times k appears in n-th row of A342585.
A347317: Version of A342585 that admits interposing null registers and reports all registers with value.
A348328: Sequence a.
Document Revision Record.
2021 1011 2120 Original version.
2021 1014 1415 Additional analysis.