The Doorman Sequence.

A sequence of David Sycamore, Mevagissey, England, 2021 0725.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 1106.

Introduction.

We consider the sequence of natural numbers A27 and set a vector of registers r(n) = n, and the greatest prime factor or gpf(x) = p, i.e., A6530(x) = p. We then generate sequence a using the following algorithm. Beginning with r(1), we attempt to find r(k) > r(n) such that gpf(k) = gpf(n). If found, we set r(k) = r(k)/p, then append r(n) to a. Since 1 is the empty product, there are no other empty products (that exceed 1), hence 1 does not appear in a, and we move on to r(2). We must write r(2) rather than 2, since it is possible that r(n) < n via reduction by some r(k) for k < n. Code 1 generates the sequence a, and we presume an offset of 2, that is, that a(n) for n ≤ 1 is not defined.

The sequence a begins:

2, 3, 2, 5, 2, 7, 2, 9, 2, 11, 4, 13, 2, 15, 2, 17, 18, 19, 4, 21, 2, 23, 8, 25, 2, 27, 4, 29, 6, 31, 2, 33, 2, 35, 12, 37, 2, 39, 40, 41, 6, 43, 4, 9, 2, 47, 16, 49, 50, 51, 4, 53, 18, 55, 8, 57, 2, 59, 12, 61, 2, 63, 2, 65, 6, 67, 4, 69, 10, 71, 24, 73, 2, 15, ...

We see a(n) ≤ n for n > 1, and that there are many fixed points such that we might define a second sequence b that lists these.

This sequence can be generated by Code 1. We have generated 1500 terms.

Examples.

Let’s run through how the first dozen or so terms come about.

We start with r(1) = 1, the empty product. Since there are no other empty products, 1 does not appear in a.

a(2) = 2 since, starting with r(2) = 2, we find r(4) = 4 exceeds r(2) and has 2 as its greatest prime factor. Hence, we set r(4) = 4/2 = 2, and r(2) = a(2) = 2.

Generally, r(p) cannot be modified on account of p prime; it calls r(2p) = 2p, the least number that exceeds p with p as greatest prime factor, setting r(2p) = 2, hence a(p) = p, and is a fixed point in a that appears in the list b.

Therefore, a(3) = 3, a(5) = 5, a(7) = 7, etc., while r(6) = 2, r(10) = 2, r(14) = 2, and each of these may not be further reduced, since they are equal to the smallest prime 2. Therefore, generally, a(2p) = 2, thus, a(4) = a(6) = a(10) = a(14) = 2. We see the term 2 often in a.

a(4) = 2 since 4 = 2p = 2². We must find r(k) > 2 such that 2 is the greatest prime factor. We know that only perfect powers 2^e for e > 1 may satisfy this condition. Therefore, we consider r(8) = 8, and reset it to 4.

a(6) = 2 for the same reason a(4) = 2; r(6) = r(2·3) was reduced to 2 by a(3) = 3; again we find r(8) = 4 satisfies and we reduce it to 2. Hence, a(8) = 2.

r(8) = a(8) = 2, therefore we reduce r(16) to 8. Eventually r(16) is whittled down to 2 by r(10) and r(12). Generally it appears that a(2^e) = 2 for e ≥ 1. Indeed, r(2^e) is the only font of admittance to any term in a that has shrunk to 2, a point of exhaustion, and since there are infinite perfect powers of 2 that appear an order of magnitude further apart as e increases, while the number of 2s in a ascribe to doubled primes and powers of 2, we will always see a(2^e) = 2. This, however is not proved.

r(9) = 9; it had not been reduced by any previous number that is 3-smooth but not a power of 2 (i.e., in A065119: 3, 6, 9, 12, 18, 24, 27, 36, 48, 54, 72, 81, 96, 108, 144, 162, …). We find r(12) > r(9) and reduce the former to 4. Therefore a(9) = 9 and is a fixed point along with the primes.

r(10) = 2 and reduces r(16) to 4 while becoming a(10).

r(12) = 4, reduces r(16) to 2 while becoming a(12).

r(14) = 2, reduces r(32) to 16 while becoming a(14), etc.

Hence a = {2, 3, 2, 5, 2, 7, 2, 9, 2, 11, 4, 13, 2}, but we have modified r(16) = 2 and r(32) = 16 thus far.

The least k > m such that gpf(k) = gpf(m).

We examine a related sequence A071830(m) = K(m) that lists the least k > m that has the same greatest prime factor as m. The sequence has offset 2.

4, 6, 8, 10, 9, 14, 16, 12, 15, 22, 18, 26, 21, 20, 32, 34, 24, 38, 25, 28, 33, 46, 27, 30, 39, 36, 35, 58, 40, 62, 64, 44, 51, 42, 48, 74, 57, 52, 45, 82, 49, 86, 55, 50, 69, 94, 54, 56, 60, 68, 65, 106, 72, 66, 63, 76, 87, 118, 75, 122, 93, 70, 128, 78, 77, 134, 85, 92, ...

Five conclusions can be drawn about the sequence.

1. K(1) is undefined, since 1 is the sole empty product.
2. K(p) = 2p for p prime.
3. K(2^e) = 2^{(e + 1)} for e > 0.
4. For m ≤ p² with gpf(m) = p, expressing m = kp, K(m) = (k + 1)p. This, since prime q > p and q − p ≥ 2.
5. For all other m = kp, K(m) = (k + j) p for some j such that gpf(k + j) = p.

We can generate terms of A071830 efficiently using Code 2 which is based on the conclusions above. It renders 2¹⁶ terms in a second and 2²⁰ terms in less than a minute.

If we are not satisfied with conclusion 5, which necessitates testing, we may examine the strictly p-smooth numbers to find m at index i.

Figure 1: Scatterplot of a(n) for 1 ≤ n ≤ 1500.

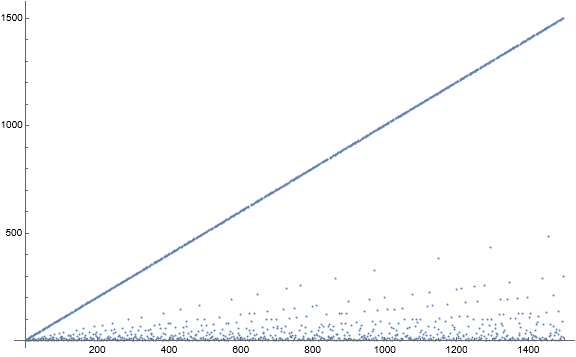
The prominent line is that of the fixed points a(n) = n. We apply a scatterplot logarithmic on both axes to orient the lines of terms evident in the plot.

Figure 2: Log-log scatterplot of a(n) for 1 ≤ n ≤ 1500.

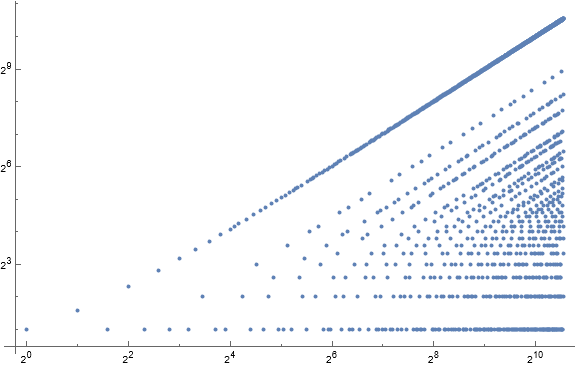
Strictly p-smooth numbers.

A number m is considered p-smooth for some prime p iff p ≤ gpf(m). Hence we place it in the sequence S_p of p-smooth numbers. As a consequence, m | P(π(p))^e, e ≥ 0, where P(n) = A2110(n). We find 2-smooth numbers S₂ = A79 (perfect powers of 2), 3-smooth S₃ = A3586, 5-smooth S₅ = A051037, etc. The sequence of 3-smooth numbers begins as shown below:

1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, 48, 54, 64, 72, 81, 96, 108, 128, 144, 162, 192, 216, 243, 256, 288, 324, 384, 432, 486, 512, 576, 648, 729, 768, 864, 972, ...

Consider numbers that are p-smooth but not q-smooth for q < p such that π(q) = π(p) − 1. We shall call such numbers “strictly p-smooth” ß_p. Therefore, we find strictly 2-smooth numbers in ß₂ = A79, 3-smooth numbers in ß₃ = A065119, 5-smooth in ß₅ = A080193, 7-smooth in ß₇ = A080194, 11-smooth in ß₁₁ = A080195, and 13-smooth in ß₁₃ = A080196. Example: the sequence of strictly 3-smooth numbers begins as follows:

3, 6, 9, 12, 18, 24, 27, 36, 48, 54, 72, 81, 96, 108, 144, 162, 192, 216, 243, 288, 324, 384, 432, 486, 576, 648, 729, 768, 864, 972, 1152, 1296, 1458, 1536, 1728, 1944, 2187, ...

Such strictly p-smooth numbers m in ß_p are those that have gpf(m) = p. Therefore ß_p ⊆ S_p, specifically, ß_p = p × S_p. So, for example, we may find ß₅ simply by 5 S₅, that is, A080193 = 5 × A051037. Hence,

p^e ⊆ ß_p ⊆ S_p,
with e ≥ 1.

We generate ß_p via Code 3.

Returning to A071830(m) = K(m) conclusion 5, for m = ß_p(i) with gpf(m) = p, K(m) = ß_p(i+1). This eliminates testing but introduces the need to generate or memoize ß_p to obtain a sufficient number of terms so as to construct ß_p(i+1) but ought to speed generation of the sequence K.

Linear features in the scatterplot.

Let s( j) for j ≥ 1 be the j-th diagonal line apparent from the top left toward the right in Figure 2. Thus, s(1) is the line of fixed points, s(2) includes the term a(4) = 2, s(3) contains a(6) = 2, a(12) = 4, that is, all terms reduced by 3. We see singleton s(4) contains a(8) and generally s(2^{(e − 1)}) contains a(2^e). The striation s(p) contains strictly p-smooth numbers that are not found in s(1), the line of fixed points in sequence b.

Conjecture: s(p) is infinite and is missing a finite number of strictly p-smooth terms in ß_p that instead appear in s(1) = b, which includes p itself.

We see that the 2s in a pertain to n = 2p and n = 2^e.

Generally, odd prime p appears only at a(p), hence only at s(1) and thus are fixed points. As a corollary, p appears once in a.

It appears a(n) = 3 for n in A138636 outside of {12, 18}, i.e., 6q for q prime that are not 3-smooth.

Conjecture: generally, a(n) = c composite for c × q outside of certain terms that appear in s(1) or are p-smooth for p ≤ gpf(c).

Fixed points.

The fixed points b populate the prominent line a(n) = n. This sequence begins:

2, 3, 5, 7, 9, 11, 13, 15, 17, 18, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 40, 41, 43, 47, 49, 50, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 77, 79, 83, 84, 85, 87, 89, 90, 91, 93, 95, 97, 99, 101, 103, 107, 109, 111, 112, 113, 115, 117, 119, 121, 123, ...

We find primes, odds, and evens in this sequence. The smallest even composite in b is 18, the smallest odd composite missing from b is 45. Indeed, we may section the fixed points by parity. Evens include the following:

2, 18, 40, 50, 84, 90, 112, 140, 154, 176, 220, 224, 234, 242, 312, 330, 338, 340, 364, 374, 396, 416, 456, 468, 494, 510, 532, 546, 608, 612, 646, 650, 680, 684, 690, 728, 748, 760, 792, 836, 874, 912, 918, 920, 928, 950, 952, 986, 988, 1012, 1044, 1058, 1156, 1178, 1216, 1218, 1224, 1240, 1242, 1254, 1288, 1360, 1364, 1368, 1392, 1426, 1450, 1456, 1482, ...

Odd composites missing from b include the following:

45, 75, 81, 105, 125, 135, 147, 165, 189, 225, 231, 243, 245, 297, 315, 325, 343, 351, 357, 375, 385, 405, 429, 441, 455, 475, 495, 507, 513, 525, 567, 595, 625, 627, 637, 663, 665, 675, 693, 715, 729, 735, 741, 765, 819, 825, 845, 847, 855, 875, 891, 897, 931, 935, 945, 957, 969, 975, 1015, 1029, 1035, 1071, 1089, 1125, 1155, 1197, 1209, 1215, 1225, 1235, 1265, 1275, 1287, 1309, 1311, 1323, 1331, 1365, 1375, 1377, 1395, 1421, 1425, 1463, 1479, 1485, ...

There doesn’t seem to be a reason, by examination of prime decomposition of these numbers, to which enter a unscathed, aside from a “sheltering” process via exhaustion of preceding registers-become-terms with the requisite gpf.

We now examine the fixed points a second way, that is, via strictly p-smooth numbers in ß(p). We find the following strictly p-smooth numbers in s(1), that is, the set of fixed points f(p).

Table 1: Strictly p-smooth numbers m that are fixed points in a, where p appears as the first term of each row.

 2
 3    9   18   27
 5   15   25   40   50   90
 7   21   35   49   63   84  112  140  175  224
11   33   55   77   99  121  154  176  220  242  ...
13   39   65   91  117  143  169  195  234  273  ...
...

Table 2: p-smooth numbers m/p that are fixed points in a:

 2:  1
 3:  1   3 : 6   9
 5:  1   3   5 : 8  10  18
 7:  1   3   5   7   9 :12  16  20  25  32
11:  1   3   5   7   9  11 :14  16  20  22 ...
13:  1   3   5   7   9  11  13  15 :18  21 ...
     ...

Hence we see that kp with odd k < q, q = prime(π(p) + 1) are certainly strictly p-smooth. (We mark the point where q would appear in Table 2 with “:”. A limited number of kp with k of any parity and strictly p-smooth also enter as fixed points. At a certain point, it seems strictly p-smooth kp is not a fixed point as k increases for each p.

At any rate, these strictly p-smooth fixed points f(p) do not appear in s(p).

This concludes our examination.

Appendix:

Code 1: Generate a(n):

Block[{a, d, k, m, r},
  Reap[
    Do[If[! IntegerQ[r[i]], Set[r[i], i]];
      Set[d, FactorInteger[r[i]][[-1, 1]]];
      Set[k, (r[i]/d) + 1];
      While[Nor[! IntegerQ[r[#]], r[#] > r[i]] &@ Set[m, k d], k++];
      If[IntegerQ[r[m]],
        r[m] /= FactorInteger[r[m]][[-1, 1]],
        Set[r[m], m/(FactorInteger[m][[-1, 1]])]];
      Sow[r[i]], {i, 2, 2^16}]
    ][[-1, -1]]
  ]

Code 2: Efficiently generate A071830:

Array[Which[
  PrimeQ[#], 2 #,
  IntegerQ@ Log2[#], 2^(IntegerExponent[#, 2] + 1),   True,
    If[#1 <= #2^2, (#1/#2 + 1) #2,
      Block[{k = #1/#2 + 1},
        While[FactorInteger[k][[-1, 1]] > #2, k++]; k #2]] & @@
          {#, FactorInteger[#][[-1, 1]]}] &[#] &, 2^16, 2]

Code 3: Efficiently generate ß_p using code that authors a nested series of loops. The text is highlighted in italic; the code writes text based on input then converts the text into an expression. (We may also generate S_p using a slightly modified version of the same code that replaces the boole statement with a textual 0).

strictlySmooth[q_, m_ : 0] :=
  Block[{w , lim}, lim = If[m <= 0, Product[Prime@ i, {i, q}], m];
    ToExpression@
      Function[w,
        StringJoin["Block[{n = ", ToString@ lim, "}, Union@ Flatten@ Table[",
          StringJoin@
            Riffle[Map[ToString@ #1 <> "^" <> ToString@ #2 & @@ # &, w],
          " * "], ", ", Most@ Flatten@ Map[{#, ", "} &, #], "]]"] &@
            MapIndexed[
              Function[p,
                StringJoin["{", ToString@ Last@ p, ", ",
                  ToString@ Boole[First[#2] == PrimePi[q]], ", Log[",
                  ToString@ First@p, ", n/(",
                  ToString@ InputForm[
                    Times @@ Map[Power @@ # &, Take[w, First@ #2 - 1]]],
                  ")]}"]]@ w[[First@ #2]] &, w]]@
                    Map[{#, ToExpression["p" <> ToString@ PrimePi@ #]} &,
                      Prime@ Range@ PrimePi[q]]
];

Concerns OEIS sequences:

A000040: The primes.
A000079: Perfect powers of 2.
A002110: The primorials, products of the smallest n primes.
A002473: 7-smooth numbers.
A003586: 3-smooth numbers.
A006530: The greatest prime factor of n, or gpf(n).
A051037: 5-smooth numbers.
A051038: 11-smooth numbers.
A065119: 3-smooth numbers that are not perfect powers of 2.
A071830: Least k > n such that gpf(k) = gpf(n)..
A080193: 5-smooth numbers that are not 3-smooth.
A080194: 7-smooth numbers that are not 5-smooth.
A080195: 11-smooth numbers that are not 7-smooth.
A080196: 13-smooth numbers that are not 11-smooth.
A080197: 13-smooth numbers.
A080681: 17-smooth numbers.
A080682: 19-smooth numbers.
A080683: 23-smooth numbers.
A138636: 6 p for p prime.

Document Revision Record.

2021 1106 2215 Draft.
2021 1107 0830 Add segments on A071830, ß_p, and code for the latter.