On the regular counting function applied to the highly composite numbers.
A301892(n) = A010846(A002182(n))
Michael De Vlieger, St. Louis, Missouri, 2018 0328 1030, revised 2018 0331 1415.
(This document is originally a text “data brief”. Data briefs intend to express observations and conjectures about sequences I’ve written. The data is the most important part of the document and can be very long. In this edition of the brief, the data is abbreviated, with links to the full analysis. Data briefs and the material in the math section of this site is intentionally starkly minimally designed so as to focus on the logic and data rather than formatting.)
We define an “n-regular” number as 1 ≤ m ≤ n such that m | ne with integer e ≥ 0. A number that is not regular is said to be “non-regular”.
The divisor d is a special case of regular number m such that d | ne with e = 0 or e = 1.
Regular numbers m can exceed n; we are concerned only with regulars m ≤ n herein.
Regular numbers, apart from 1, occupy the cototient of n. The union of the regulars and the cototient leaves us with the “semitotative” for composite n > 6 listed in row n of A272619.
We are not concerned with “semidivisors” m such that m | ne with e > 1, listed in row n of A272618, but with the regular and divisor counting functions A010846(n) and A000005(n),
respectively.
Contents.
Table 1: Comparison of A010846(A002182(n)) and A002183(n).
Table 2: A301893(i) = Numbers k that set records for the ratio rcf(k)/τ(k).
Table 3: The intersection of A002182 and A244052.
(Observations and conjectures follow each table.)
Code.
Table 1: Comparison of A010846(A002182(n)) and A002183(n).
Questions:
- How many regular numbers do the highly composite numbers have, given that the divisor is a special case of regular number?
- Do they also set records for the regular counting function (i.e., are the highly composite numbers also "highly regular")?
- Are the HCNs representative of numbers that set records for the ratio rcf(k)/τ(k)?
(1) A002182(n)
(2)
Index of A002182(n) in A244052. If A002182(n) is not in A244052, left blank.
(3) Index of A002182(n) in A301893 (see Table 2). (A301893 computed through 36 × 106).
(4) A301893(n) = numbers k that set records for the ratio rcf(k)/τ(k).
(5) A301892(n) = A010846(A002182(n)).
(6) A108602(n) = A001221(A002182(n)).
(7) A002183(n)/A301892(n)
(8) “Multiplicity Family” of A002182(n): MN( m/A002110(A108602(m)) ). (See Table 4).
MN = Multiplicity Notation = A054841(a(n)) here represents the reverse of A054841 in OEIS; i.e., “little-endian” rather than big-endian, e.g., A054841(84) = 1013 but here it is 2101. We use A054841 or “multiplicity notation” here since the terms of a(n) are products of relatively small primes and the notation succinctly expresses their prime decomposition. This is notation Achim Flammenkamp employed in his studies of highly composite numbers.
| n | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
| --- | -------- | ----- | ----- | ----- | ----- | ---------- | ---- | ------- |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 2 | 2 | 2 | 2 | 2 | 1 | 1 | 0 | |
| 3 | 4 | 3 | 3 | 3 | 1 | 1 | 1 | |
| 4 | 6 | 4 | 2 | 4 | 5 | 0.8 | 2 | 0 |
| 5 | 12 | 6 | 6 | 8 | 0.75 | 2 | 1 | |
| 6 | 24 | 8 | 8 | 11 | 0.727273 | 2 | 2 | |
| 7 | 36 | 9 | 14 | 0.642857 | 2 | 11 | ||
| 8 | 48 | 10 | 15 | 0.666667 | 2 | 3 | ||
| 9 | 60 | 11 | 12 | 26 | 0.461538 | 3 | 1 | |
| 10 | 120 | 14 | 16 | 36 | 0.444444 | 3 | 2 | |
| 11 | 180 | 16 | 18 | 44 | 0.409091 | 3 | 11 | |
| 12 | 240 | 20 | 49 | 0.408163 | 3 | 3 | ||
| 13 | 360 | 24 | 58 | 0.413793 | 3 | 21 | ||
| 14 | 720 | 30 | 76 | 0.394737 | 3 | 31 | ||
| 15 | 840 | 22 | 32 | 131 | 0.244275 | 4 | 2 | |
| 16 | 1260 | 24 | 36 | 156 | 0.230769 | 4 | 11 | |
| 17 | 1680 | 26 | 40 | 174 | 0.229885 | 4 | 3 | |
| 18 | 2520 | 48 | 206 | 0.23301 | 4 | 21 | ||
| 19 | 5040 | 60 | 266 | 0.225564 | 4 | 31 | ||
| 20 | 7560 | 64 | 308 | 0.207792 | 4 | 22 | ||
| 21 | 10080 | 72 | 339 | 0.212389 | 4 | 41 | ||
| 22 | 15120 | 80 | 388 | 0.206186 | 4 | 32 | ||
| 23 | 20160 | 84 | 428 | 0.196262 | 4 | 51 | ||
| 24 | 25200 | 90 | 460 | 0.195652 | 4 | 311 | ||
| 25 | 27720 | 47 | 96 | 766 | 0.125326 | 5 | 21 | |
| 26 | 45360 | 100 | 550 | 0.181818 | 4 | 33 | ||
| 27 | 50400 | 108 | 568 | 0.190141 | 4 | 411 | ||
| 28 | 55440 | 120 | 979 | 0.122574 | 5 | 31 | ||
| 29 | 83160 | 128 | 1124 | 0.113879 | 5 | 22 | ||
| 30 | 110880 | 144 | 1238 | 0.116317 | 5 | 41 | ||
| 31 | 166320 | 160 | 1411 | 0.113395 | 5 | 32 | ||
| 32 | 221760 | 168 | 1548 | 0.108527 | 5 | 51 | ||
| 33 | 277200 | 180 | 1659 | 0.108499 | 5 | 311 | ||
| 34 | 332640 | 192 | 1754 | 0.109464 | 5 | 42 | ||
| 35 | 498960 | 200 | 1983 | 0.100857 | 5 | 33 | ||
| 36 | 554400 | 216 | 2048 | 0.105469 | 5 | 411 | ||
| 37 | 665280 | 224 | 2160 | 0.103704 | 5 | 52 | ||
| 38 | 720720 | 240 | 3689 | 0.065058 | 6 | 31 | ||
| 39 | 1081080 | 256 | 4211 | 0.060793 | 6 | 22 | ||
| 40 | 1441440 | 288 | 4617 | 0.062378 | 6 | 41 | ||
| 41 | 2162160 | 320 | 5245 | 0.061011 | 6 | 32 | ||
| 42 | 2882880 | 336 | 5731 | 0.058629 | 6 | 51 | ||
| 43 | 3603600 | 360 | 6135 | 0.05868 | 6 | 311 | ||
| 44 | 4324320 | 384 | 6482 | 0.059241 | 6 | 42 | ||
| 45 | 6486480 | 400 | 7308 | 0.054735 | 6 | 33 | ||
| 46 | 7207200 | 432 | 7539 | 0.057302 | 6 | 411 | ||
| 47 | 8648640 | 448 | 7949 | 0.056359 | 6 | 52 | ||
| 48 | 10810800 | 480 | 8477 | 0.056624 | 6 | 321 | ||
| 49 | 14414400 | 504 | 9198 | 0.054795 | 6 | 511 | ||
| 50 | 17297280 | 512 | 9681 | 0.052887 | 6 | 62 | ||
| 51 | 21621600 | 576 | 10306 | 0.05589 | 6 | 421 | ||
| 52 | 32432400 | 600 | 11515 | 0.052106 | 6 | 331 | ||
| 53 | 36756720 | - | 640 | 19994 | 0.03201 | 7 | 32 | |
| 54 | 43243200 | - | 672 | 12448 | 0.053985 | 6 | 521 | |
| 55 | 61261200 | - | 720 | 23259 | 0.030956 | 7 | 311 | |
| 56 | 73513440 | - | 768 | 24532 | 0.031306 | 7 | 42 | |
| 57 | 110270160 | - | 800 | 27570 | 0.029017 | 7 | 33 | |
| 58 | 122522400 | - | 864 | 28408 | 0.030414 | 7 | 411 | |
| 59 | 147026880 | - | 896 | 29917 | 0.02995 | 7 | 52 | |
| 60 | 183783600 | - | 960 | 31849 | 0.030142 | 7 | 321 | |
| 61 | 245044800 | - | 1008 | 34500 | 0.029217 | 7 | 511 | |
| 62 | 294053760 | - | 1024 | 36278 | 0.028227 | 7 | 62 | |
| 63 | 367567200 | - | 1152 | 38557 | 0.029878 | 7 | 421 | |
| 64 | 551350800 | - | 1200 | 43016 | 0.027897 | 7 | 331 | |
| 65 | 698377680 | - | 1280 | 77028 | 0.016617 | 8 | 32 | |
| 66 | 735134400 | - | 1344 | 46436 | 0.028943 | 7 | 521 | |
| 67 | 1102701600 | - | 1440 | 51652 | 0.027879 | 7 | 431 | |
| 68 | 1396755360 | - | 1536 | 93907 | 0.016357 | 8 | 42 | |
| 69 | 2095133040 | - | 1600 | 105210 | 0.015208 | 8 | 33 | |
| 70 | 2205403200 | - | 1680 | 61730 | 0.027215 | 7 | 531 | |
| 71 | 2327925600 | - | 1728 | 108330 | 0.015951 | 8 | 411 | |
| 72 | 2793510720 | - | 1792 | 113928 | 0.015729 | 8 | 52 | |
| 73 | 3491888400 | - | 1920 | 121118 | 0.015852 | 8 | 321 | |
| 74 | 4655851200 | - | 2016 | 130970 | 0.015393 | 8 | 511 | |
| 75 | 5587021440 | - | 2048 | 137566 | 0.014887 | 8 | 62 | |
| 76 | 6983776800 | - | 2304 | 146038 | 0.015777 | 8 | 421 | |
| 77 | 10475665200 | - | 2400 | 162599 | 0.01476 | 8 | 331 | |
| 78 | 13967553600 | - | 2688 | 175323 | 0.015332 | 8 | 521 | |
| 79 | 20951330400 | - | 2880 | 194715 | 0.014791 | 8 | 431 | |
| 80 | 27935107200 | - | 3072 | 209588 | 0.014657 | 8 | 621 | |
| 81 | 41902660800 | - | 3360 | 232236 | 0.014468 | 8 | 531 | |
| 82 | 48886437600 | - | 3456 | 241387 | 0.014317 | 8 | 4211 | |
| 83 | 64250746560 | - | 3584 | 440351 | 0.008139 | 9 | 52 | |
| 84 | 73329656400 | - | 3600 | 266983 | 0.013484 | 8 | 3311 | |
| 85 | 80313433200 | - | 3840 | 467403 | 0.008216 | 9 | 321 | |
| 86 | 97772875200 | - | 4032 | 286547 | 0.014071 | 8 | 5211 | |
| 87 | 128501493120 | - | 4096 | 529244 | 0.007739 | 9 | 62 | |
| 88 | 146659312800 | - | 4320 | 316236 | 0.013661 | 8 | 4311 | |
| 89 | 160626866400 | - | 4608 | 561065 | 0.008213 | 9 | 421 | |
| 90 | 240940299600 | - | 4800 | 623240 | 0.007702 | 9 | 331 | |
| 91 | 293318625600 | - | 5040 | 373244 | 0.013503 | 8 | 5311 | |
| 92 | 321253732800 | - | 5376 | 670993 | 0.008012 | 9 | 521 | |
| 93 | 481880599200 | - | 5760 | 743774 | 0.007744 | 9 | 431 | |
| 94 | 642507465600 | - | 6144 | 799574 | 0.007684 | 9 | 621 | |
| 95 | 963761198400 | - | 6720 | 884524 | 0.007597 | 9 | 531 | |
| 96 | 1124388064800 | - | 6912 | 918857 | 0.007522 | 9 | 4211 | |
| 97 | 1606268664000 | - | 7168 | 1002878 | 0.007147 | 9 | 522 | |
| 98 | 1686582097200 | - | 7200 | 1014877 | 0.007094 | 9 | 3311 | |
| 99 | 1927522396800 | - | 7680 | 1048383 | 0.007326 | 9 | 631 | |
| 100 | 2248776129600 | - | 8064 | 1088291 | 0.00741 | 9 | 5211 | |
| 101 | 3212537328000 | - | 8192 | 1185830 | 0.006908 | 9 | 622 | |
| 102 | 3373164194400 | - | 8640 | 1199750 | 0.007202 | 9 | 4311 | |
| 103 | 4497552259200 | - | 9216 | 1284854 | 0.007173 | 9 | 6211 | |
| 104 | 6746328388800 | - | 10080 | 1413882 | 0.007129 | 9 | 5311 | |
| 105 | 8995104518400 | - | 10368 | 1512270 | 0.006856 | 9 | 7211 | |
| 106 | 9316358251200 | - | 10752 | 2607576 | 0.004123 | 10 | 521 | |
| 107 | 13492656777600 | - | 11520 | 1661238 | 0.006935 | 9 | 6311 | |
| 108 | 18632716502400 | - | 12288 | 3095217 | 0.00397 | 10 | 621 | |
| 109 | 26985313555200 | - | 12960 | 1946228 | 0.006659 | 9 | 7311 | |
| 110 | 27949074753600 | - | 13440 | 3417004 | 0.003933 | 10 | 531 | |
| 111 | 32607253879200 | - | 13824 | 3547008 | 0.003897 | 10 | 4211 | |
| 112 | 46581791256000 | - | 14336 | 3864992 | 0.003709 | 10 | 522 | |
| 113 | 48910880818800 | - | 14400 | 3910396 | 0.003682 | 10 | 3311 | |
| 114 | 55898149507200 | - | 15360 | 4037208 | 0.003805 | 10 | 631 | |
| 115 | 65214507758400 | - | 16128 | 4188170 | 0.003851 | 10 | 5211 | |
| 116 | 93163582512000 | - | 16384 | 4557034 | 0.003595 | 10 | 622 | |
| 117 | 97821761637600 | - | 17280 | 4609691 | 0.003749 | 10 | 4311 | |
| 118 | 130429015516800 | - | 18432 | 4931474 | 0.003738 | 10 | 6211 | |
| 119 | 195643523275200 | - | 20160 | 5419232 | 0.00372 | 10 | 5311 | |
| 120 | 260858031033600 | - | 20736 | 5791113 | 0.003581 | 10 | 7211 | |
| 121 | 288807105787200 | - | 21504 | 10174493 | 0.002114 | 11 | 521 | |
| 122 | 391287046550400 | - | 23040 | 6354166 | 0.003626 | 10 | 6311 | |
| 123 | 577614211574400 | - | 24576 | 12036043 | 0.002042 | 11 | 621 | |
| 124 | 782574093100800 | - | 25920 | 7431427 | 0.003488 | 10 | 7311 | |
| 125 | 866421317361600 | - | 26880 | 13263098 | 0.002027 | 11 | 531 | |
| 126 | 1010824870255200 | - | 27648 | 13758600 | 0.00201 | 11 | 4211 | |
| 127 | 1444035528936000 | - | 28672 | 14970020 | 0.001915 | 11 | 522 | |
| 128 | 1516237305382800 | - | 28800 | 15143047 | 0.001902 | 11 | 3311 | |
| 129 | 1732842634723200 | - | 30720 | 15625881 | 0.001966 | 11 | 631 | |
| 130 | 2021649740510400 | - | 32256 | 16200656 | 0.001991 | 11 | 5211 | |
| 131 | 2888071057872000 | - | 32768 | 17604683 | 0.001861 | 11 | 622 | |
| 132 | 3032474610765600 | - | 34560 | 17805134 | 0.001941 | 11 | 4311 | |
| 133 | 4043299481020800 | - | 36864 | 19029413 | 0.001937 | 11 | 6211 | |
| 134 | 6064949221531200 | - | 40320 | 20884747 | 0.001931 | 11 | 5311 | |
| 135 | 8086598962041600 | - | 41472 | 22298971 | 0.00186 | 11 | 7211 |
Observations
(These observations do not include those well-known by those interested in HCNs)
- The ratio τ(x)/rcf(x) for x = A002182(n) generally declines as x increases. This implies that for numbers that set records in the divisor counting function, the number of regular numbers is very much higher as n increases.
- Only 13 HCNs are also “highly regular”, i.e., appear in A244052. The largest HCN that is also highly regular is 27720, the 25th HCN and the 47th highly regular number. This seems to be associated with the fact that the prime decomposition of numbers in A002182 involves “more enriched” small primes as n increases, while the numbers in A244052 are either squarefree or in A060735.
- Only 2 and 6 set records for the ratio τ(x)/rcf(x). In other words, the highly composite numbers seem generally not representative of the highest possible ratio of number of divisors to the number of regulars.
- The value of A301892(n) jumps when ω(n) increases, in line with what we would expect of the regular counting function regarding not-necessarily squarefree products of n versus (n + 1) smallest primes.
Conjectures
- The intersection of A002182 and A244052 is finite, consisting of 13 terms:
{1, 2, 4, 6, 12, 24, 60, 120, 180, 840, 1260, 1680, 27720}.
All of these terms are also in A060735 and not in A288813, as the latter are squarefree and have "gaps" among prime divisors.
This intersection has the following number of terms in the "tiers" 0 through 5 of A244052:
{1, 2, 3, 3, 3, 1}.
A "tier" n consists of all terms m in A244052 with A002110(n) ≤ m < A002110(n + 1).
If we look at A060735 as a number triangle T(n,k) = k × A002110(n) with 1 ≤ k < prime(n + 1),
the terms are:
{0, 1},
{{1,1}, {1,2}},
{{2,1}, {2,2}, {2,4}},
{{3,2}, {3,4}, {3,6}},
{{4,4}, {4,6}, {4,8}},
{5,12}
(It is this observation that spurred development of Tables 3, 4, 6, and Graph 5.) - If it is true that the only non-squarefree terms in A301893(n) are {18, 150}, then
the intersection of A002182 and A301893(n) is finite and consists of {1, 6}. (see Table 2 Conjecture 1).
Table 2: A301893(i) = Numbers k that set records for the ratio rcf(k)/τ(k).
Question:
- What numbers set records for the ratio of the regular counting function and the divisor counting function?
(1) k = A301893(i)
(2) Index of A301893(i) in A244052. If A301893(i) is not in A244052, left blank.
(3) rcf(k) = A010846(k).
(4) τ(k).
(5) τ(k)/rcf(k)
PC(n) = A287352(n) is the "pi-code" or first differences of indices of prime divisors p of n, e.g., A287352(60) = 1,0,1,1 since 60 = 2 × 2 × 3 × 5. The terms are delimited by (.).
| i | k = (1) | (2) | (3) | (4) | (5) | PC(k) |
| --- | -------- | ----- | ----- | ----- | ---------- | ---------- |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 2 | 6 | 4 | 5 | 4 | 0.8 | 1.1 |
| 3 | 10 | 5 | 6 | 4 | 0.666667 | 1.2 |
| 4 | 18 | 7 | 10 | 6 | 0.6 | 1.1.0 |
| 5 | 22 | 7 | 4 | 0.571429 | 1.4 | |
| 6 | 30 | 9 | 18 | 8 | 0.444444 | 1.1.1 |
| 7 | 42 | 10 | 19 | 8 | 0.421053 | 1.1.2 |
| 8 | 66 | 22 | 8 | 0.363636 | 1.1.3 | |
| 9 | 78 | 23 | 8 | 0.347826 | 1.1.4 | |
| 10 | 102 | 25 | 8 | 0.32 | 1.1.5 | |
| 11 | 114 | 26 | 8 | 0.307692 | 1.1.6 | |
| 12 | 138 | 27 | 8 | 0.296296 | 1.1.7 | |
| 13 | 150 | 15 | 41 | 12 | 0.292683 | 1.1.1.0 |
| 14 | 174 | 29 | 8 | 0.275862 | 1.1.8 | |
| 15 | 210 | 17 | 68 | 16 | 0.235294 | 1.1.1.1 |
| 16 | 330 | 18 | 77 | 16 | 0.207792 | 1.1.1.2 |
| 17 | 390 | 19 | 80 | 16 | 0.2 | 1.1.1.3 |
| 18 | 510 | 86 | 16 | 0.186047 | 1.1.1.4 | |
| 19 | 570 | 88 | 16 | 0.181818 | 1.1.1.5 | |
| 20 | 690 | 94 | 16 | 0.170213 | 1.1.1.6 | |
| 21 | 870 | 101 | 16 | 0.158416 | 1.1.1.7 | |
| 22 | 1110 | 106 | 16 | 0.150943 | 1.1.1.9 | |
| 23 | 1230 | 110 | 16 | 0.145455 | 1.1.1.10 | |
| 24 | 1290 | 112 | 16 | 0.142857 | 1.1.1.11 | |
| 25 | 1410 | 114 | 16 | 0.140351 | 1.1.1.12 | |
| 26 | 1590 | 118 | 16 | 0.135593 | 1.1.1.13 | |
| 27 | 1770 | 121 | 16 | 0.132231 | 1.1.1.14 | |
| 28 | 1830 | 122 | 16 | 0.131148 | 1.1.1.15 | |
| 29 | 2010 | 126 | 16 | 0.126984 | 1.1.1.16 | |
| 30 | 2130 | 128 | 16 | 0.125 | 1.1.1.17 | |
| 31 | 2190 | 130 | 16 | 0.123077 | 1.1.1.18 | |
| 32 | 2310 | 29 | 283 | 32 | 0.113074 | 1.1.1.1.1 |
| 33 | 2730 | 30 | 295 | 32 | 0.108475 | 1.1.1.1.2 |
| 34 | 3570 | 31 | 313 | 32 | 0.102236 | 1.1.1.1.3 |
| 35 | 3990 | 32 | 322 | 32 | 0.099379 | 1.1.1.1.4 |
| 36 | 4830 | 339 | 32 | 0.094395 | 1.1.1.1.5 |
(See full table of 1114 rows in this text file.)
Observations
- There are 2 non-squarefree terms {18, 150} less than 36 × 106.
- No primes p appear in A301893. This is because all regular m divide p, and since all the regulars of 1 also divide 1, no primes appear in A301893. If we were to ignore 1, then the prime 2 would set a record for the ratio of rcf(k)/τ(k).
- The values of τ(A301893(i)) are in A000079, i.e., powers 2e except e = 1 (see number 2 above).
- Aside from the 2 non-squarefree terms, many terms m are products of A002110(j) × ph, with h > j between some lower and upper bound outside of when m is in A002110. Example: 30 is in A002110; {42, 66, 78, 102, 114, 138, 174} are A002110(3) × ph with 2 ≤ h ≤ 8.
- There are a few terms of the form A002110(j) × pg × ph, with h > g > j + 1. In other words, there is a gap in the indices of the prime divisors between the 3rd and 2nd largest prime divisors, as well as one potentially between the 2nd and largest prime divisors. The smallest m of this type is 46410 = 2 × 3 × 5 × 7 × 13 × 17, followed by 51870 = 2 × 3 × 5 × 7 × 13 × 19.
- Regarding A001221(A301893(i)), the sequence seems to be divided into “tiers” wherein ω(A301893(i)) either increases or holds as i increases. Thus we might speak of “tiers” for all terms m ≤ A002110(6) = 30030. However, 36330 immediately follows 30030 in the sequence and ω(36330) = 5. For m > 30030, the numbers m with omega of a particular value are increasingly mixed with terms that have a different value. These intermingled “tiers” do seem to have a floor and ceiling. The tiers consist of terms as described in number 3 above:
- Tier 0 contains {1}.
- There is no tier 1 since this would contain numbers m with ω(m) = 1.
- Tier 2 contains {6, 10, 18, 22}; 12 is missing since rcf(12)/τ(12) = 8/6 was bested by 10 with ratio 6/4. Otherwise, A002110(1) × h with 1 ≤ h ≤ 4 and h ≠ 3, also excepting the term 18.
- Tier 3 contains A002110(2) × h with 1 ≤ h ≤ 8, as well as 150 = 2 × 3 × 5².
- Tier 4 contains A002110(3) × h with 1 ≤ h ≤ 18, and h ≠ 8.
- Tier 5 contains A002110(4) × h with 1 ≤ h ≤ 30. This tier is interrupted by A002110(6) as before mentioned, but continues after 30030 with 36 ≤ h ≤ 38. There are further intrusions of numbers with ω(m) = 6, as well as missing values in the range 47 ≤ h ≤ 356. The 5th tier seems to terminate at A301893(319) = A002110(7), whereinafter no number with ω(5) appears.
- “Tier” 6 has a floor at A002110(6) and its ceiling has not yet been seen in computation.
- “Messy bands” of terms m in A244052 appear in A301893. The indices j of these terms m in A244052 appear as follows, usually with significant intrusions of A301893 not in A244052:
- A244052 tier 0: j = 1 at i = 1.
- A244052 tier 2: j = {4, 5, 7} starting at A301893(3) = 6 = A002110(2); includes the non-squarefree 18.
- A244052 tier 3: j = {9, 10, 15} starting at A301893(6) = 30 = A002110(3); includes the non-squarefree 150.
- A244052 tier 4: 17 ≤ j ≤ 19 at 15 ≤ i ≤ 17 respectively. (A301893(15) = 210 = A002110(4)).
- A244052 tier 5: 29 ≤ j ≤ 32, at 32 ≤ i ≤ 35 respectively. (A301893(32) = 2310 = A002110(5)).
- A244052 tier 6: 48 ≤ j ≤ 53 starting at A301893(62) = 30030 = A002110(6).
- A244052 tier 7: 72 ≤ j ≤ 77 starting at A301893(319) = 510510 = A002110(7).
- A244052 tier 7: 104 ≤ j ≤ 111* starting at A301893(777) = 9699690 = A002110(8).
* it is unclear whether this is the maximum value of j for m in A244052 tier 7.
Conjectures
- The only non-squarefree terms in A301893 are 18 and 150.
- Primorials A002110(j) for j = 0 and j > 2 appear in A301893.
- Aside from 18 and 150, there are a few of the smallest terms k in tier t of A244052 in A301893. These terms are squarefree and also appear in A288813.
- There will always be “intrusions” of m of ω(m) < t among terms k in tier t of A244052 with t > 6, equating to m ≥ A002110(6) i.e., m ≥ 30030. Corollary to this is that the ranges j = 1, 17 ≤ j ≤ 19 and 29 ≤ j ≤ 32 in A244052 are the only contiguous terms of A244052 tier t in A301893.
Table 3: The intersection of A002182 and A244052.
Based on Conjecture 1.1, we re-examine the terms m that are in both A002182 and A244052, then produce a chart plotting them with n = primorial A002110(ω(m)) and k = m/A002110(ω(m)).
The intersection of A002182 and A244052 is finite, consisting of 13 terms: {1, 2, 4, 6, 12, 24, 60, 120, 180, 840, 1260, 1680, 27720}. All of these terms are also in A060735 and not in A288813, as the latter are squarefree and have “gaps” among prime divisors. This intersection has the following number of terms in the “tiers” 0 through 5 of A244052:
{1, 2, 3, 3, 3, 1}.
A “tier” n consists of all terms m in A244052 with A002110(n) ≤ m < A002110(n + 1). If we look at A060735 as a number triangle T(n,k) = k × A002110(n) with 1 ≤ k < prime(n + 1), the terms are plotted below. The top figure is the coordinates (n,k) in A060735. The middle figure is the decimal number, and the bottom set of numbers delimited by “.” are the exponents of the prime pertaining to the place in which the exponent appears. For example, “2.1.1” → 2² × 3 × 5 = 60.

Observations
- The terms in the multiplicity notations of these numbers hold or decrease. For k = 3 or k = 5, we would have 1.2, 1.2.1, 1.2.1.1, or 1.1.2, 1.1.2.1, 1.1.2.1.1, etc. Such configurations of prime divisors are absent from terms in A002182.
- If we were to extend the irregular triangle beyond k < p(n + 1), then we could perhaps plot all terms of A002182 on a grid. In the grid below, dots “.” appear for terms in A060735, if not occupied by a term in A002182, which if in A060735 is followed by an asterisk. These dotted and asterisked positions are fully occupied by many but not all terms in A244052 and illustrates some of the “divergence” of the two record-setter sequences.

- Since we observe the terms plotted on a grid tend to occupy certain values of k, we might condense the grid and merely annotate coordinates for each of the terms. We can use
{ω(m),m/A002110(ω(m))} = {A108602(i), A002182(i) / A002110(A108602(i))} to furnish T(n,k).
Continuing investigation.
Note: the consideration of Table 3 has led to further investigation that continues at this data brief.
If we take the investigation quite far, we can produce the following graph of {m/A002110(ω(m)), ω(m)}, eliminating columns m/A002110(ω(m)) without HCNs. The black pixels represent an HCN (i.e., m in A002182) while the red pixels represent an SHCN (i.e., m in A002201, also in A002182, since A002201 is a subset of A002182). The HCNs plotted here derive from [1], while the SHCNs plotted in red derive from my processing the b-file at A000705.
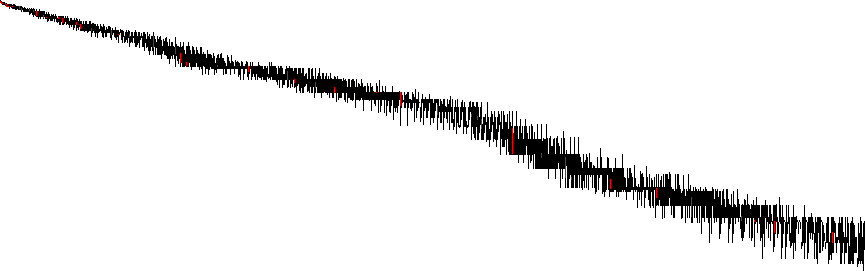
Concerns sequences:
A000005: Divisor counting function τ(n), i.e., number of numbers 1 ≤ d ≤ n such that d | ne with 0 ≤ e ≤ 1.
A000079: Nonnegative integer powers of 2.
A001221: ω(n) = Number of distinct prime divisors of n.
A002110: The primorials.
A002182: Highly composite numbers, i.e., where records are set in A000005.
A002183: Records in A000005 = A000005(A002182(n)).
A010846: Regular counting function, abbreviated rcf(n), i.e., number of numbers 1 ≤ m ≤ n such that m | ne with e ≥ 0.
A054841: For n = Product_pe, write ek in the k-th place, or write 0 if pk does not divide n.
A060735: Irregular triangle read by rows: T(n, k) = k × A002110(n) for 1 ≤ k < prime(n + 1).
A108602: A001221(A002182(n)).
A244052: Highly regular numbers, i.e., where records are set in A010846.
A288813: Irregular triangle read by rows: T(m, k) is the list of squarefree numbers A002110(m) < t < 2 × A002110(m) such that A001221(t) = m.
A301892: a(n) = A010846(A002182(n)).
A301893: Where records occur in A010846(n)/A000005(n).
See [2] for these and other A-number sequences in this work.
References
[1]: Achim Flammenkamp, “Highly Composite Numbers”, retrieved 2018 0329 2330 GMT. Downloads appear at the bottom of page and require “gunzip” application.
[2]: Neil Sloane, The Online Encyclopedia of Integer Sequences, retrieved 2018 0329 2330 GMT. See “Concerns Sequences” for individual links.
Original text-format data brief can be seen here.
////// Revision Record //////
201803281015 Created.
201803281330 A301892 extended to 115 terms.
201803281945 A301892 extended to 125 terms.
201803282030 Table 3 added.
201803290830 A301892 extended to 135 terms.
201803290845 Converted Table 1 last column to MN( A002182(n)/A002110(A108602(n)) ).
201803310845 Data brief converted to HTML; portion ascribed to A301413 partitioned.
201803311415 Improved tables and charts.
(Updated 29 March 2018)