 |
Alpha-2 FactorGlossary |
Alpha-2 (α2) Factor
Consider the number base n. An alpha-2 factor tα2 is an integer necessarily coprime to n that divides α2 = (n² + 1). In base n, α2 = (n² + 1) is always written “101”, assuming standard positional notation and Hindu-Arabic-like numerals.
In base n, the alpha-2 factor tα2 enjoys special properties that can facilitate work with these numbers.
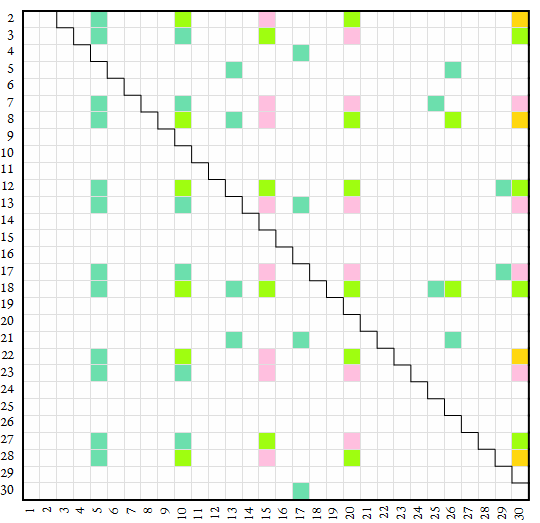
The map below plots alpha-2 factors in green (tα2 ■) and semicoprime alpha-2-regular inheritors in yellow-green (sα2 ■). Products of alpha-2 factors with neighbor factors, coprime to base n, appear in pink, while products of alpha-2 factors with neighbor factors and n-regular numbers, semicoprime to base n, appear in gold. Number base n appears on the vertical axis and digit k appears on the horizontal.
Divisibility test for alpha-2 factors
The base-n divisibility test applying to a factor of (n² + 1), involves the pairing of base-n digits beginning with the unit digit and working towards significance (meaning leftward from the radix point), then taking the alternating sum of the numbers formed by these digit pairs.
For instance, we know that octal “3641100” is divisible by 5 since we add “3 − 64 + 11 − 00” = “−61 + 11” = “−50”, and octal “50” is clearly divisible by 5. Thus octal “3641100” = decimal 1,000,000 is divisible by 5.
The same test works in base 12. We know that duodecimal “402854” is divisible by 5 since we add “40 − 28 + 54” = “68”, and duodecimal “68” is clearly divisible by 5. Thus duodecimal “402854” = decimal 1,000,000 is divisible by 5.
The test constitutes convenient methods for testing for divisibility by the number 5 in bases 8, 12, and 18 (or any base n ≡ ±2 (mod 5)). In octal and duodecimal, these tests for fivefoldness are effective since the multiples of 5 less than the hundredlike square of base might be easily memorized. In societies using these bases, we might anticipate this “rule of 5” to be rather important as five, though not as small as 3, is a rather common prime factor.
The alpha-2 test that applies to 5 in bases n ≡ ±2 (mod 5), which includes octal and duodecimal, completes a system of divisibility tests for 5 such that there is always a test for 5 in any nonzero positive integer number base. In bases n divisible by 5, we have the regular test. In bases 5k + 1, we have the omega test, and in bases 5k − 1 we have the alpha test. Since there is always a divisibility test for the numbers 2−6, we have compound tests for any factor of 60 as well in every base.
Since the alpha-2 test (also known as the alternating digit sum test over digit blocks of size 2) is a practical solution to determine whether x is divisible by k = 5 in bases n that are 2 or 3 larger than a multiple of 5, we may see the alpha-2 test commonly in such bases. It might be known as the “Rule of 5” in such bases. This rule would require one to memorize the multiples of 5 less than the hundred-like, n², therefore there is a human-cognitive practicality limit that applies to such rules. Regarding k = 5, the rule would likely be practical for bases 2 (binary), 3, 7, 8 (octal), 12 (duodecimal), and 13.
Unvigesimal (base 21) is a sort of toolbox for detection of divisibility by the smallest 7 primes. Of course, 3 and 7 are divisors with the regular divisibility test. Since 5 | (21 − 1), we can use the digit sum to check for divisibility by 5. Since 11 | (21 + 1), we can use the alternating sum to check for divisibility by 11. Finally, we can use the alpha-2 tests to check for divisibility by 13 and 17. In fact, with the exception of 16 and 19, all unvigesimal digits possess some workable and non-modular divisibility test. In contrast, regarding the non-modular divisibility tests for the smallest 7 primes, decimal only cover 2, 3, 5, and 11, and duodecimal just 2, 3, 5, 11, and 13.
Source [1] conflates the alpha-2 divisibility test simply an alternating-sum-of-digits “trick” (in the parlance of the paper) involving a block of 2 digits.
Numbers k that are alpha-2 for some base n
Generally, numbers k such that sqrt(−1) mod k exists (OEIS A008784 aside from 1 and 2, see comment 3 by Todorov) occur as alpha-2 for some base n.
Alpha-2-regular inheritors
An alpha-2-regular inheritor (sα2 ■) is a necessarily composite sα2= r × tα2 semicoprime to n such that the coprime factor tα2 divides (n² + 1) and the regular factor r is practical. Armed with a regular divisibility test for r and an alpha-2 divisibility test for tα2, we can use a compound divisibility test for the alpha-2 inheritor sα2. In base 12, given the above-mentioned test for 5 and the duodecimal evenness test, we can determine whether an arbitrary duodecimal number x is divisible by ten. Example: the above-mentioned duodecimal number “402854” is known to be divisible by five; we know it is also divisible by ten since it ends in one of {0, 2, 4, 6, 8, a}, where “a” = digit ten. This is akin to the decimal divisibility test for 6; we know if a number is divisible by three and is even, it is divisible also by 6.
Other alpha-2 inheritors
We can produce alpha-2 inheritors using neighbor factors (i.e., factors of alpha (n + 1) and of omega (n − 1)). These show as pink in the map above.
The alpha-2-alpha factor is a necesarily composite tα2α= tα × tα2, a product of 2 factors that are coprime to base n such that tα2 divides (n² + 1) and tα divides (n + 1). Here, we combine the alpha divisibility rule for tα and the alpha-2 divisibility rule for tα2 to arrive at a compound divisibility test for tα2α. These apply to the following:
For k = 15, base n mod k ≡ 2 or 8, which includes binary, octal, bases 17 and 23, etc.
For k = 20, base n mod k ≡ 3 or 7, which includes bases 3, 7, 23, 27, etc.
For k = 30, base n mod k ≡ 17 or 23, which includes bases 17 and 23, etc.
The alpha-2-omega factor is a necesarily composite tα2ω= tω × tα2, a product of 2 factors that are coprime to base n such that tα2 divides (n² + 1) and tα divides (n − 1). Here, we combine the omega divisibility rule for tω and the alpha-2 divisibility rule for tα2 to arrive at a compound divisibility test for tα2ω.
For k = 15, base n mod k ≡ 7 or 13, which includes bases 7, 13, 22, 28, etc.
For k = 20, base n mod k ≡ 13 or 17, which includes bases 13, 17, 33, 37, etc.
For k = 30, base n mod k ≡ 7 or 13, which includes bases 7, 13, 37, 43, etc.
To test for k = 60 in base n = 43, we can combine the alpha-2 test for 5 and the omega-2 test for 12.
Furthermore, we can combine several tests based on prime power factors to produce compound tests for certain numbers k. For instance, we can express k = 60 as 3 × 4 × 5. In base n = 28, 3 | (28 − 1), 4 | 28², and 5 | (28² + 1). Therefore we can use the omega test for 3, the regular test for 4 (examining 2 last digits) and the alpha-2 test for 5 to determine if a number is divisible by 60 in octovigesimal (base 28). These show as gold in the map above.
Base-n expansion of 1/tα2
Alpha-2 factors tα2 > 1 in the denominator 1/tα2 have a 4 digit purely recurrent expansion in base n, as the recurrent period of 1/tα2 is 4. In decimal, octal, 1/5 = .14631463… and in duodecimal same is .24972497…. In base 3, the tenth is .00220022… since 10 = 3² + 1. The thirteenth expressed in quinary (base 5) is .01430143….
The base-n expansions of alpha-2 inheritors sα2 involve at least one nonrepeating digit associated with the regular factor r and 4 recurrent digits associated with the alpha-2 (coprime) factor tα2. The number of nonrepeating digits is the richness ε of the n-regular factor r. If r | n, (i.e., r is a divisor of n), then there will be only one nonrepeating digit, since r | nε with ε = 1.
The table below diagrams the behavior of numbers k at the top as unit fractions 1/k, with bold numerals nonrepeating, italic repeating. The alpha-2 numbers and their factors tα2 > 1 appear in dark green while the alpha-2 inheritors are highlighted in yellow-green (■) with regular factor, in muted yellow green with alpha factor (■), and in muted green with omega factor (■).
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 2 | 1 | 01 | 01 | 0011 | 001 | 001 | 001 | 000111 | 00011 | 0001011101 | 0001 | 000100111011 | 0001 | 0001 | 0001 |
| 3 | 1 | 1 | 02 | 0121 | 01 | 010212 | 01 | 01 | 0022 | 00211 | 002 | 002 | 001221 | 00121 | 0012 |
| 4 | 2 | 1 | 1 | 03 | 02 | 021 | 02 | 013 | 012 | 01131 | 01 | 010323 | 0102 | 01 | 01 |
| 5 | 2 | 13 | 1 | 1 | 04 | 032412 | 03 | 023421 | 02 | 02114 | 02 | 0143 | 013431 | 013 | 0124 |
| 6 | 3 | 2 | 13 | 1 | 1 | 05 | 043 | 04 | 03 | 0313452421 | 03 | 024340531215 | 023 | 02 | 0213 |
| 7 | 3 | 2 | 15 | 1254 | 1 | 1 | 06 | 053 | 0462 | 0431162355 | 04 | 035245631421 | 03 | 0316 | 03 |
| 8 | 4 | 25 | 2 | 1463 | 125 | 1 | 1 | 07 | 06314 | 0564272135 | 052 | 0473 | 04 | 0421 | 02 |
| 9 | 4 | 3 | 4 | 17 | 14 | 125 | 1 | 1 | 08 | 07324 | 06 | 062 | 057 | 053 | 05 |
| 10 | 5 | 3 | 25 | 2 | 16 | 142857 | 125 | 1 | 1 | 09 | 083 | 076923 | 0714285 | 06 | 0625 |
| 11 | 5 | 37 | 28 | 2 | 19 | 163 | 14 | 124986 | 1 | 1 | 0a | 093425a17685 | 087 | 08 | 0762 |
| 12 | 6 | 4 | 3 | 2497 | 2 | 186a35 | 16 | 14 | 12497 | 1 | 1 | 0b | 0a35186 | 09724 | 09 |
| 13 | 6 | 4 | 3 | 27a5 | 2 | 1b | 18 | 15a | 13b9 | 12495ba837 | 1 | 1 | 0c | 0b36 | 0a74 |
| 14 | 7 | 49 | 37 | 2b | 249 | 2 | 1a7 | 17ac63 | 158 | 13b65 | 1249 | 1 | 1 | 0d | 0c37 |
| 15 | 7 | 5 | 3b | 3 | 27 | 2 | 1d | 1a | 17 | 156c4 | 13b | 124936dca5b8 | 1 | 1 | 0e |
| 16 | 8 | 5 | 4 | 3 | 2a | 249 | 2 | 1c7 | 19 | 1745d | 15 | 13b | 1249 | 1 | 1 |
| 17 | 8 | 5b | 4 | 36da | 2e | 274e9c | 2 | 1f | 1bf5 | 194adf7c63 | 17 | 153fbd | 13afd6 | 1249 | 1 |
| 18 | 9 | 6 | 49 | 3ae7 | 3 | 2a5 | 249 | 2 | 1e73a | 1b834g69ed | 19 | 16gb | 152a | 13ae7 | 1249 |
| 19 | 9 | 6 | 4e | 3f | 3 | 2dag58 | 27 | 2 | 1h | 1dfa6h538c | 1b | 18ebd2ha475g | 16ehc4 | 15 | 13ad |
| 20 | a | 6d | 5 | 4 | 36d | 2h | 2a | 248hfb | 2 | 1g759 | 1d6 | 1af7dgi94c63 | 18b | 16d | 15 |
| 21 | a | 7 | 5 | 4 | 3a | 3 | 2d | 27 | 2 | 1j | 1f | 1cj8 | 1a | 18 | 16bh |
| 22 | b | 7 | 5b | 48hd | 3e | 3 | 2gb | 29h | 248hd | 2 | 1i7 | 1f5 | 1c | 1a5j | 185b |
| 23 | b | 7f | 5h | 4di9 | 3j | 36d | 2k | 2chka5 | 26kg | 2 | 1l | 1hfl57 | 1ei | 1c63 | 1a |
| 24 | c | 8 | 6 | 4j | 4 | 3a6kdh | 3 | 2g | 29e | 248haljf6d | 2 | 1k795cm3geib | 1h3a6kd | 1e9 | 1c |
| 25 | c | 8 | 6 | 5 | 4 | 3e7 | 3 | 2jb | 2c | 26kb9 | 2 | 1n | 1jg | 1g | 1e |
| 26 | d | 8h | 6d | 5 | 48h | 3iem7b | 36d | 2n | 2f | 29bl7 | 248h | 2 | 1m7b3ie | 1j | 1g6d |
| 27 | d | 9 | 6k | 5alg | 4d | 3n | 3a | 3 | 2io8 | 2c79m | 26k | 2 | 1p | 1lg5a | 1if5 |
| 28 | e | 9 | 7 | 5gmb | 4i | 4 | 3e | 3 | 2mb5g | 2f7hmpcka5 | 29 | 248h6cpnjalf | 2 | 1o7d | 1l |
| 29 | e | 9j | 7 | 5n | 4o | 4 | 3i | 36cpmg | 2q | 2id57qafnl | 2c | 26k | 2 | 1r | 1ng9 |
| 30 | f | a | 7f | 6 | 5 | 48h | 3mf | 3a | 3 | 2logar85dj | 2f | 296rkn | 248h | 2 | 1q7f |
| ........... | ............ | ............... | ........... |
Color Canon
The colors used to represent alpha-2 factors in this work appear in the table below:

References
[1] Marc Renault, Stupid Divisibility Tricks, (See PDF), Section 3.3, Math Horizons (2006). Retrieved in June 2019.