Glossary

Home

Glossary

This glossary briefly defines concepts used in this work. The concepts usually link to pages with expanded definitions, references, and further information. (This glossary is continually updated before the official live date of this website.) Terms followed by an asterisk (*) are terms coined by the author or herein usually for convenience. Many of the terms in the glossary feature links to standard definitions, the MathsIsFun more basic and appropriate for middle school students, the PrimePages and MathWorld more professional and appropriate for university math students.

A

Addend — a number that we add to another number to obtain a sum. See the MathsIsFun or MathWorld definition.

Addition — written a + b = c, the operation of finding the difference c between a and b. We can thus say c − b = a or c − a = b, as addition is the inverse operation of subtraction. The numbers a and b are addends, and c the sum. See the MathsIsFun or MathWorld definition.

Alpha Number (α ■, enhanced ■) — regarding base n, the number (n + 1). In base 10, α = 11. Alpha is coprime to base, but has semiminimum period 2. Therefore alpha or any of its factors in the denominator has a 2-digit purely recurrent expansion in base n. In decimal, 1/11 = .090909…. In octal, 9 is alpha and is written “11”; “1/11” = .070707… and 1/3 = .252525…. Base n divisibility tests for alpha involve taking the alternating sum of digits of x. If the sum is an integer multiple of α, then so is x. Decimally, 14641 is divisible by 11 since (1 + 6 + 1) − (4 + 4) = 8 − 8 = 0 is an integer multiple of 11 (note: 14641 = 11⁴). In any base n, α is written “11” and its small multiples kα with 1 ≤ k ≤ (n − 1) are a pair of the same digit. (Color canon: ta, #c8dcb2, enhanced: taa, #00aaa0)

   Alpha Factor (t_α ■, enhanced ■) — a divisor of the number α = (n + 1). t_α | (n + 1) implies GCD(t_α, n) = 1. In base n, the behavior of α also ascribes to its factors t_α. In base 15, the number 16 is alpha; its factors (greater than 1) are 2, 4, 8, and 16 (which in pentadecimal is written “11”). The alternating sum divisibility tests ascribe to 2, 4, 8. In base 15, 1/2 = .777…, 1/4 = .3b3b3b…, and 1/8 = .1d1d1d…. We note here that since 15 is an odd base, 2 | 14 and 2 | 16 (it is an alpha-omega factor), and its behavior (i.e., a single repeating digit) appears instead to ascribe to (n − 1). (Color canon: ta, #c8dcb2, enhanced: taa, #00aaa0)

   Alpha-Omega Factor (t_αω ■, enhanced ■) — the number 2 in an odd base n divides both the even neighbors ω = (n − 1) and α = (n + 1). The behavior of 2 in odd bases is the same as the omega factor. (Color canon: tb, #c8c4e8, enhanced: tbb, #803090)

Alpha Test — See “Alpha Divisibility Test”.

Alternating Digit Sum — the adding of all the even-ordered and all the odd-ordered digits of an integer separately, then subtracting one sum from the other. The alternating sum of 58564 is (5 + 5 + 4) − (8 + 6) = 14 − 14 = 0. The alternating sum of digits of a number is useful in the alpha intuitive divisibility test.

Arbitrary — something chosen at random or done according to whim. We speak of an “arbitary number” and mean the selection of any nonzero positive integer. The term is used to show that a method might be applied to any number.

Argam* (Numerals) — an extension of the Hindu Arabic numerals to cover transdecimal number bases. The term derives from Arabic, meaning “numbers”. The singular of “argam” is “ragam”.

Arithmetic — a branch of mathematics that primarily deals with integers and computation. The branch includes the basic operations like addition and multiplication, but also the factorization of integers and divisibility tests. The field of number theory is also called “higher arithmetic”. See the MathsIsFun or MathWorld definitions.

   Modular Arithmetic — the determination of remainder (residue) in a division problem n ÷ k = x + r written n ≡ r (mod k). Oftentimes the clock is used as an example, modular arithmetic seen as "clock arithmetic", since we are only interested in the remainder m in the division problem. On the 12-hour clock, k = 12, and we might say 16 ÷ 12 = 1 + 4, or 16 ≡ 4 (mod 12). We observe 8 + 9 ≡ 5 (mod 12), thinking 9 hours after 8 am is 5 pm. Modular arithmetic is not the focus of this work, yet it does provide a toolset to determine divisibility and divisibility tests in any base. Of the most importance to us, the congruence n ≡ 0 (mod k) implies k | n, that is, k is a divisor of n. For an online introduction, consider Khan Academy. A succinct, advanced description appears at Stanford. See the MathWorld definition.

Arithmetic Relationship — a connection between one number and another based on arithmetic or number-theoretical qualities. The greatest common denominator is an example; gcd(6, 10) = 2, since 2 is the largest number that divides both; gcd(3, 10) = 1 since 3 and 10 have no prime factor in common. Corollary to this are statements like 5 | 10 (read “5 divides 10”) or 3 is coprime to 10. The counting functions relate a number to a kind of entity. The prime counting function π(n) yields the number of primes not exceeding n: π(10) = 4 since there are four primes (2, 3, 5, 7) that do not exceed 10.

   Constitutive (Arithmetic) Relationship* — in this work, the term refers to one of three mutually exclusive states (apart from the number 1) of the nonzero integer k with respect to integer base n. These are n-regular, n-semicoprime, or n-coprime, with the number 1 both regular and coprime to n. An n-regular number k divides some perfect power n^e. An n-coprime number k has no prime factor in common with n. An n-semicoprime number k is nonregular and noncoprime to n. The divisor d is a special case of n-regular number. Numbers that have arithmetic relationship to the squarefree kernel rad(n) have the same relationship to any number with the same set of distinct prime factors of rad(n). For instance, the set of numbers {1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, …} are regular to 6, but also to 12, 18, 24, 36, 48, 72, etc.; any of the numbers in the set are regular to any multiple of 6.

B

Base, Number (Radix) — a number, usually an integer n > 1, that is used as the scale of a number system that represents an arbitary number x in terms of sums of products of coefficients that are numeral (usually) 1 ≤ k < n and perfect powers of the base, n^ε. We can convert a (decimal) number x to base n by dividing x by n recursively, noting the remainders and proceeding till we have exhausted the number x. For instance, we can convert the number 217 to base 6 as follows: 218/6 = 36 R2, 36/6 = 6 R0, 6/6 = 1 R0, 1/6 = 0 R1; taking the first remainder as the smallest digit, we have 218 = 1002₆.
This work uses the term “base” as it is the more publicly common term, though “radix” would seem less confusing, as multiple important concepts in mathematics use the word “base”. See MathsIsFun, MathWorld, or Prime Pages definitions.

   Alternating Base — a mixed radix system where the base alternates across at least every other place. In decimal coded sexagesimal,

   Auxiliary Base* — a number a in base n that facilitates divisibility by many small integers. Decimal auxiliary bases include 12, 60, and 360; these are used in systems of measure of length, time, and angle. The use of 60 minutes in an hour enables division of the hour by 1, 2, 3, 4, 5, 6, 10, 12, 20, 30, and 60 integer parts, emphasizing the divisions by 2, 3, 4, 6, 12 by sacrificing divisibility by 5 and 10. We speak of 5-, 10-, 15-, and 30-minute intervals more often than 6- or 12-minute intervals, which are 1/10 and 1/5 of an hour respectively. The apparently round sixths, quarters, and thirds conveyed by decimal 60 are said to be “clean” compared to the apparently less-round fifths and tenths. In base 12, 60 would not make a good auxiliary base, since 12 is already highly divisible itself, and we might be left using strictly duodecimal measures. A hexadecimal auxiliary base might be 240.

   Coded Base — See Coded Base.

   Mixed Radix — a nonstandard number system wherein the base changes across each position. A simple example of a mixed radix system is the reckoning of time. Consider the duration of weeks, days, hours, minutes, and seconds; in this system, we have 7 days to the week, 24 hours to the day, 60 minutes to the hour and same number of seconds to the minute. We might note the bases in this system as 7:24:60:60. Thus, we could express a million seconds as 1, 4, 13, 46, 40, or 1 week, 4 days, 13 hours, 46 minutes, and 40 seconds.

Benford’s Law — See the MathWorld or Prime Pages definitions.

Bigendian — a method of writing terms such that the most significant comes first. The standard positional notation we use today is bigendian: the number 123, has hundreds written first. The expression of time of day is bigendian: hours come before minutes, which come before seconds.

Binary — The number system based on 2, representing all numbers using the numerals 0 and 1. Binary digits are often called bits. See MathsIsFun or MathWorld definitions.

Bit — a binary digit, i.e., one of the digits of n expressed in base 2. A binary numeral either 0 or 1. See the MathWorld definition.

Bitwise — having to do with the digits of n expressed in base 2.

Boolean Function — a function relating to logic, resulting in a strictly true or false value. See the MathWorld definition.

   Boolean And — The Boolean and(x, y) function is true when both x and y are true.

   Boolean Not — The function not(x) is true if x is false, or false if x is true.

   Boolean Or — The Boolean or(x, y) function is true when either x and y are true, or both are true.

   Boolean Xor — The function xor(x, y) is true when either x and y are true, but false when both are true.

Borrow — in subtraction, the decrementation of the

Byte — a group of 8 binary digits, also called an “octet” especially in France. A byte equates to 2 hexadecimal digits (i.e., 2 nybbles), 4 quaternary digits, or a single base-256 (hexaducentoquinquagesimal) digit. See the MathWorld definition.

C

Canonical — regarding mathematics, the standard or conventional method when a number of possible methods might be used. See the MathWorld definition.

   Color Canon — See “Color Canon”.

Carry — in addition, the incrementation of the immediately-larger place when the coefficient in the place under addition meets or exceeds base n. Example: in base ten, consider 17 + 6. The sum of the units digits is 13 ≥ 10, thus we retain 3 in the units place, and increment the next larger place to 2, thus we have 17 + 6 = 23. See the MathWorld definition or the MathsIsFun interactive demonstration of addition.

In multiplication, the addition of digits outside of the place under multiplication to the next larger place. Decimally, 15 × 9 has the unit place contain 45; we keep the 5 and add 4 to the product 1 × 9 = 9. Thus we have 135 as the final product. See the MathsIsFun interactive demonstration of multiplication.

Centovigesimal — a number system based on 120.

Ceiling Function — a function rounds a non-integer to the next integer. The ceiling of the number π = 3.14159… is 4, but the ceiling of the integer 3 is 3. See the MathWorld or Prime Pages definition.

Clean* — said of the representation of a number in a base, either auxiliary or as used, either as terminating fraction or integer, with the fewest number of significant digits.

Coded Base — a usually large number base n whose digits are represented in base m < n.

Coding Base — a number 1 < m < n, integers, with m a divisor of a large n, used to break the span of n into smaller sub-digits or figures so that more than one figure is required to represent a place value in the alternating positional notation of base n. Example: in decimal-coded sexagesimal commonly used in the expression of time, we express base-60 digits decimally. Thus, 1:40 pm is a two-digit sexagesimal number where the digit 40 is expressed by two decimal digits 4 and 0.

Coefficient — in the base-n positional notation of a real number x, digit k in the ε-th place is the coefficient of the perfect power n^ε and has the value kn^ε. Example. In the decimal number 32.5, the coefficient in the tens place is 3. In decimal-coded sexagesimal, the number 6:40 (as perhaps in the notation of time of day), the coefficient in the units (or minutes) place is the decimal number 40; the 4 is the decade-figure and the 0 is the unit-figure.

Color Canon — the colors by which this work codes various relationships between integers k > 0 and bases n.

Complement — (regarding sets) all elements that are in a larger set A but not in B. The set of numbers in A = 1 ≤ k ≤ n that are not divisors of n the complement of the set B of divisors of n. For n = 10, set A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, set B = {1, 2, 5, 10}, and the complement of B is {3, 4, 6, 7, 8, 9}. See the MathsIsFun or MathWorld definition.

Composite — An integer that is the multiple of at least 2 primes. A composite number has more than 2 divisors. Per the Unique Factorization Theorem, a composite is any integer n > 1 that is not prime. See the MathsIsFun, MathWorld, or PrimePages definition.

   Highly Composite — numbers n that set records for the number of divisors (i.e., the divisor counting function). {1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, …}. In this sequence, 6 has 4 divisors, 10 has as many, but 12 has 6 divisors. See OEIS A002182, or Achim Flammenkamp’s technical data. See the MathWorld definition.

   Largely Composite — numbers n such that have as many or more divisors than all numbers k < n. {1, 2, 3, 4, 6, 8, 10, 12, 18, 20, 24, 30, 36, 48, 60, 72, …}. In this sequence, 12 has 6 divisors; 18 and 20 have as many, but 24 has 8 divisors. Sequence attributed to Ramanujan, see OEIS A067128.

   Superior Highly Composite — numbers n whose ratio τ(n)/n^e > τ(k)/k^e for some e > 0, for all k > 1 (τ(n) is the divisor counting function). See OEIS A002201, or the MathWorld definition.

Composition* — a term used in this work that refers to the prime decomposition of n. Example: 60 = 2 × 2 × 3 × 5, thus the composition of 60 is {2, 2, 3, 5}.

Compound, Regular* — A term used in this work to signify an n-regular number g that is the product of some nonzero positive perfect power of the base, n^ε and a proper regular γ. Regular numbers g that are not proper regulars in base n are called regular compounds. Example: the number 5³ = 125 is a decimal proper regular, since it is not divisible by n = 10. We can generate a family of compound regulars using the form g = γn^ε with ε ≥ 0. Thus, 1250, 12,500, 125,000, etc. are compound regulars generated by g = 125 × 10^ε.

Congruency — an integer k is described as congruent to m modulo n if n is a divisor of (k − m).

Constitutive Relationship* — See “Constitutive Arithmetic Relationship”.

Coprime (adjective) — nonzero integers k and n having greatest common divisor 1 (i.e., GCD(k, n) = 1). In other words, k and n are not both divisible by any prime p. In this work, the term is preferred over “relatively prime”, “k prime to n”, etc. for succinct clarity, to eliminate confusion with the term “prime”. These terms are equivalent to “coprime”. See MathWorld or PrimePages definitions (of “relatively prime”).

Coprime (noun) — a number t that is coprime to the base. The numbers 1 ≤ t < n that are coprime to the base are called totatives of that base. Coprimes of rad(n) (the squarefree kernel of n) are also coprime to any number with the same distinct prime factors as n. The coprime relationship is one of the three constitutive arithmetic relationships.

   Alpha Coprime (t_α ■, enhanced: ■) — a number that divides α = (n + 1). In octal, the numbers 3 and 9 are alpha coprimes. (Color canon: ta, #c8dcb2, enhanced: taa, #00aaa0)

   Alpha-2 Coprime (t_α2, enhanced: ■) — a number that divides α = (n² + 1) but not any neighbor of n. In octal, the numbers 5 and “15” = thirteen are alpha-2 coprimes. (Color canon: enhanced: ta, #c8dcb2)

   Alpha Omega Coprime (t_αω ■, enhanced: ■) — the number 2 in an odd base. (Color canon: tb, #c8c4e8, enhanced: tbb, #803090)

   Coprime Factor — the coprime component of a number semicoprime to n. See “Coprime Factor”.

   Coprime and Regular — the number 1 divides base n since 1 divides all numbers, and is coprime to base n since GCD(1, n) = 1.

   Omega Coprime (t_ω ■, enhanced: ■) — a number that divides ω = (n − 1). Decimally, 3 and 9 are omega coprimes (totatives). (Color canon: to, #c8dee8, enhanced: too, #0070c0)

   Omega-2 Coprime (t_ω2, enhanced: ■) — a number that divides α = (n² − 1) but not any neighbor of n. Decimally, the numbers 33 and 99 are omega-2 coprimes. The numbers 3 and 9 divide (10 − 1) = 9 and are omega coprimes, and 11 = (10 + 1), the decimal alpha number. (Color canon: enhanced: to, #c8dee8)

   Opaque Coprime (t, ■) — a number coprime to base that is not a neighbor factor. (Color canon: t, #e8e9ea)

Cototient — the set of integers 1 < k < n whose elements k have at least one prime factor p that divides n. These are the numbers that are not coprime to n, and thus are not counted by the Euler totient function φ(n). For n = 10, the cototient includes {2, 4, 5, 6, 8, 10}, since the totatives of 10 are {1, 3, 7, 9}. The nondivisors in the cototient of 10 are {4, 6, 8}; these are the neutral numbers of 10 less than 10.

Counting function — an arithmetic function that yields the number of entities in a given domain.
   Divisor counting function — τ(n) — the number of divisors of the integer n. See OEIS A000005, MathWorld definition.
   Euler totient function — φ(n) — the number of totatives of the integer n (i.e., reduced residues mod n). See OEIS A000010, MathWorld, or Prime Pages definition.
   Neutral counting function — ξ(n) — the number of neutral numbers less than or equal to n. See OEIS A045763.
   Prime counting function — π(n) — the number of primes less than or equal to n. See OEIS A000720, MathWorld definition.
   Regular counting function — RCF(n) or r(n) — the number of n-regular numbers less than or equal to n. See OEIS A000005.
   Semidivisor counting function — ξ_d(n) — the number of semidivisors less than the integer n. See OEIS A243822.
   Semitotative counting function — ξ_t(n) — the number of semitotatives of the integer n. See OEIS A243823.

Cube — a number x multiplied by itself twice, written x³. The number 27 is the cube of 3, since it is 3 × 3 × 3.

D

Decimal — base 10 number system, rarely “denary”. We often use the adverb “decimally” to convey the notion that something is done “in decimal,” that is, with ten as the base. See MathWorld definition. See an introduction at MathsIsFun.

   Decimal Point — a symbol, in the United States usually a period (full stop, “.”) and in Europe a comma (“,”), that demarcates the integer part from the fractional part of a number represented in standard positional notation in base 10. This is the decimal radix point, the term “radix point” applies to any base.

   Decimal Coded — an adjective that describes a base n > 10 whose digits are written in decimally, usually with leading zeros to fill the n-places. Decimal coded sexagesimal is the most commonly seen variety and is in everyday use worldwide to express time. We write “3:20” and understand this to mean three hours and twenty minutes (a minute is sixty to the hour), which is tantamount to saying 3 and one third hours. We write “2:05”, the minute using a leading zero to maintain two decimal places per sexagesimal place. Decimal coded sexagesimal is an ideal auxiliary base as it provides flexibility to decimal though the sacrifice of clean representations of fivefoldness to obtain clean representations of threefoldness. Using decimal as a coding base eliminates the need for novel transdecimal numerals. We note that base 12 is decimal coded in the common am/pm manifestation of hours, but we do not generally note leading zeros.

Decomposition, Prime Power — the expression of an integer n as a product of prime powers: n = p₁^e1 × p₂^e2 × … × p_k^ek. Normally these prime powers are sorted such that the smallest prime appears first. For example, 1920 = 2⁶ × 3 × 5.

Denominator — in a ratio n/d, integers, d ≠ 0, the number d is the denominator. See MathsIsFun or MathWorld definition.

Decrement — the reduction of an integer k by 1; k − 1. If k = 5, decrementing k has k = 4.

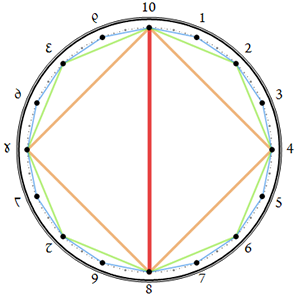
Diagram, Geometric — (cyclic diagram) a graphic plotting regular d-sided polygons at same scale, with one vertex aligned, centered on the same point, for all divisors d > 1 of n. Below, the polygons with the number of sides corresponding to the divisors of 16 are plotted in a clock-like dial. For the case of d = 2, we plot a “digon”, a “2-sided polygon”.

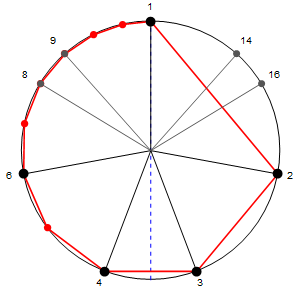
Diagram, Logarithmic — (logarithmic wheel) a polar graphic such that the circle indicates the base-n logarithmic mantissae with 0 and 1 aligned. The graphic is normally made to portray proper n-regular numbers k to a certain richness e. Below, the red line joins the numbers 1 ≤ k < n, the dashed blue line indicates the square root of 12, and the plotted points, noted in duodecimal are the proper regular numbers of 12 to richness 2. (The term “log wheel” we attribute to Wendy Y. Krieger).

Difference — the result of subtracting. The difference between 6 and 4 is 2. See MathsIsFun or MathWorld definitions.

Digit — One of the coefficients in the standard positional notation of a number x expressed in some base n, normally n is understood to be 10. Also, one of the symbols (also called numerals) that represent an integer 0 ≤ k < n used in the standard positional notation of arbitrary numbers x expressed in base n. See MathWorld definition. In this work, we refer to symbols that represent integers 0 ≤ k < n as “numerals”, while place values are referred to as digits.

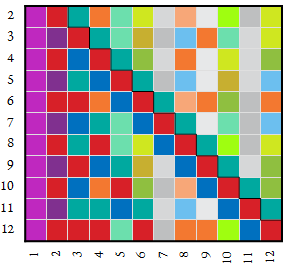
   Digit Map — a chart that uses a color code to indicate the arithmetic relationship of numbers 1 ≤ k ≤ n with base n. The sample below pertains to base 120. Red numbers are divisors of 120, orange and shades of peach are regular to 120. Factors of 119 appear in dark blue and factors of 121 appear in teal. Opaque totatives appear in various grays. The colors shown here adhere to the color canon used in this work. (See this link for more on the maps.)

The maps numbers k represented in many bases n can be made into a compendium that, at least for small bases n, can facilitate the comparison of bases. The vertical axis of the map below applies to bases n, while the horizontal axis applies to the number k. This map shows all flavors of arithmetic relationship studied in this work, colored according to the color canon.

   Significant Digit — a coefficient k in the base-n expansion in standard positional notation that helps establish the number x beyond its magnitude. The significand is made up of significant digits. In the decimal number 108,000, “108” is the significand made up of three significant digits. The number 7.125 is completely made up of significant digits. Finally, 0.09375 has the significand “9375”. In standard positional notation, the least significant digit is the rightmost in the significand, while the most significant digit is the leftmost. Another way of approaching this definition is that a significant digit helps establish the mantissa of the logarithm of a number. (This definition differs from the notion of scientific notation and significant figures used in technical writing.)

Digital Root — the digit that is the result of adding the digits of an integer x again and again. For instance, the digital root of decimal 19683 is 1 + 9 + 6 + 8 + 3 = 27, 2 + 7 = 9.

Digitwise* (adjective) — having to do with the range of digits or numerals of base n.

Divide, to (verb) — An integer k is said to divide integer n if the result of division is also an integer k′. This is abbreviated “k | n”, read “k divides n”. This is equivalent to saying that k is a divisor or factor of n. See MathWorld or PrimePages definition.

   “evenly divide” — See “Divide, to”. The term is used in some sources and is equivalent to k | n. We avoid it in this source to avoid confusion with the term “even”.

Dividend — for a and b ≠ 0, written either a ÷ b = c or a/b = c, we call the number a the dividend. See the MathsIsFun or MathWorld definition.

Divisibility — the determination that an arbitrary number x is divisible by a usually small number k, all nonzero integers. The number x is divisible by k if and only if there is a nonzero integer m such that k × m = x. For instance, the number 10 is divisible by 2 since 2 × 5 = 10; 9 is not divisible by 2 since 9/2 = 4.5, which is not an integer.

   Divisibility Rule — See “Divisibility Test”.

Divisibility Test — A method involving examination or manipulation of the base-n digits of the arbitrary integer x intended to determine whether x is divisible by a usually small integer k. This method is normally practical, meaning that it is faster than dividing x/k. If the test is easily memorized by an average person, this work calls such a test “intuitive”. Examples: the decimal evenness test, see if x ends in 0, 2, 4, 6, or 8, or for divisibility by 3, add the digits of x; if the sum is divisible by 3, x is divisible by 3. Some tests are not as well-known despite their being around since the Talmud (the left trim 1 test for divisibility by 7). See MathsIsFun or MathWorld definitions. See Marc Renault’s summary of a variety of decimal divisibility tests, and Eric L. McDowell’s Divisibility Tests — a History and User’s Guide in the MAA Convergence. See this page for simple divisibility rules for numbers 2 ≤ k ≤ 8 in any base n > 1.

   Compound Divisibility Test — a divisibility test that combines two or more tests based on mutually coprime factors. Such tests pertain to necessarily composite n-semicoprime numbers k, and we break k = r × t into its regular factor r and coprime factor t (with respect to base n), which are implicitly mutually coprime. For instance, given the decimal divisibility tests for 2 (a regular test) and 3 (an omega test), we can derive a test for 6. If a number x is even and the sum of its digits is divisible by 3, then x is divisible by 6. We know 216 is divisible by 6 since 2 + 1 + 6 = 9 (divisible by 3) and it is even. If one knows left- and right-trim tests, these might also be combined. For instance, given the right-trim rule for divisibility by 7 involving 2, we can test for divisibility by 28. We know 784 (split into 7,84 for the 7 rule) is divisible by 28 since it is even and 84 − (2 × 7) = 84 − 14 = 70, which is clearly divisible by 7. We cannot apply such a rule to a prime power (such as 16) since there is no way to divide the number into mutually coprime factors.

   Intuitive Divisibility Test* — a divisibility test in base n that seems related to the number tested and is easily borne in mind by the average person. For the purposes of this work, we limit the IDTs to the regular and the neighbor-factor divisibility tests. Some left- and right-trim tests are simple, for instance the decimal left-trim test pertaining to 7. A number x is divisible by 7 if we take the leftmost digit, multiply it by 2, and add the sum to the rest of the digits. If the result is divisible by 7 so is x. 343 is divisible by 7 since 3 × 2 = 6, 43 + 6 = 49, and 49 is clearly divisible by 7. Though this test is simple, it involves remembering we need to double the leftmost digit, whereas doubling and divisibility by 7 are not necessarily intuitive to the average person. Any number that does not have a regular or neighbor-factor divisibility test or any composite for which all prime power factors are resolved via a combination thereof is said to be “opaque” in base n.

   Regular Divisibility Test* — a test for divisibility by n-regular k, meaning a nonzero integer k | n^e with richness e ≥ 0. This includes divisibility tests for divisors d. Such tests involve examining the last e digits of an arbitrary integer x and seeing whether this group is one of n^e/k combinations (n^e/k is the multiplicative complement of k), each with e digits. The evenness test is a regular test for all even bases. The decimal test for divisibility by 25 is a practical regular test: x is divisible by 25 if the last 2 digits of x are one of {00, 25, 50, 75}. Regular intuitive divisibility tests (i.e., those of this format) are not practical for numbers that have high richness. The decimal intuitive divisibility test for 16 requires examining the last 4 digits of x to see if the group is one of 625 4-digit combinations. Only low-richness n-regular numbers have practical regular divisibility tests.

   Modular Divisibility Test — a divisibility test for integer k in base n using a residue d (mod k) congruent to n². We break the base-n digits of arbitrary integer x into a and b (i.e., the number “12345” into a = “1” and b = “2345”). Then we take b − da = m; if m is divisible by k, then so is x.

      Left Trim Divisibility Test — a modular divisibility test for integer k in base n using a residue d (mod k) congruent to n², involving breaking an arbitrary integer x into groups a and b (i.e., the number “12345” into a = “1” and b = “2345”). Then we take b − da = m; if m is divisible by k, then so is x. There are left trim tests involving at least 1 leftmost digit; the number used based on what seems practical.

      Right Trim Divisibility Test — a modular divisibility test for integer k in base n using a residue d (mod k) congruent to n², involving breaking an arbitrary integer x into groups a and b (i.e., the number “12345” into a = “1234” and b = “5”). Then we take b − da = m; if m is divisible by k, then so is x. There are right trim tests involving at least 1 rightmost digit; the number used based on what seems practical.

   Neighbor-Factor Divisibility Test — a base-n test for divisibility by a factor of (n − 1) or (n + 1) (i.e., any factor of (n² − 1)), or 2 for odd bases n. These tests are practical so long as addition in base n is practical and the number of digits is reasonable.

      Alpha Divisibility Test — the base-n intuitive divisibility test for a factor of alpha α = (n + 1). This test involves the alternating sum of the digits of the arbitrary integer x. The test pertains to 11 in base 10: a number x is divisible by 11 if we add all every other digit of x, and then add all the other digits we hadn't added first, subtracting one sum from the other. If the result is divisible by 11, so is x. We can tell 1771561 is divisible by 11, since (1 + 7 + 5 + 1) − (7 + 1 + 6) = 14 − 14 = 0, which is a multiple of 11. This rule is seldom necessary, but in octal, the alpha rule applies to 3. In octal, “46343” is divisible by 3 since (4 + 3 + 3) − (6 + 4) = “12” − “12” = (1 + 2) − (1 + 2) = 3 − 3 = 0, which is a multiple of 3.

      Alpha-Omega Divisibility Test — the evenness test in an odd base, which is simply the omega divisibility test, though the more arduous alpha test also works. Example, in base 15, we know “1716061” is divisible by 2 since (1 + 7 + 1 + 6 + 0 + 6 + 1) = “17”, (1 + 7) = 8, which is clearly divisible by 2. Alternatively, (1 + 1 + 0 + 1) − (7 + 6 + 6) = 3 − “14” = “−11” (i.e., decimal 16), which is also clearly divisible by 2. (Pentadecimal “1716061” = decimal 16,777,216 = 2²⁴).

      Omega Divisibility Test — the base-n intuitive divisibility test for a factor of omega ω = (n − 1). This test involves the digit sum (or digital root) of the arbitrary integer x. If the sum of these digits is divisible by x, so is x. In base 10, we have the Rule of 9. We add the digits of x; if the sum is divisible by 9, so is x. This rule also pertains to decimal 3 since 3 is a factor of 9. In base 12, the rule applies (quite uselessly) to 11. In hexadecimal, the omega rule applies to 3, 5, and digit-15 (but not to 9, since 9 is not a factor of 15).

   Power-Neighbor-Factor Divisibility Test — a base-n test for divisibility by a factor of (n² − 1) or (n² + 1) that does not divide (n − 1) or (n + 1).

      Alpha-2 Divisibility Test — the base-n divisibility test applying to a factor of (n² + 1), involving the pairing of base-n digits beginning with the unit digit and working towards significance (meaning leftward from the radix point), then taking the alternating sum of the numbers formed by these digit pairs. For instance, we know that octal “3641100” is divisible by 5 since we add “3 − 64 + 11 − 00” = “−61 + 11” = “−50”, and octal “50” is clearly divisible by 5. Thus octal “3641100” = decimal 1,000,000 is divisible by 5. The same test furnishes convenient methods for the number 5 in bases 12 and 18. In octal and duodecimal, these tests for fivefoldness are effective since the multiples of 5 less than the hundredlike square of base might be easily memorized. In societies using these bases, we might anticipate this “rule of 5” to be rather important as five, though not as small as 3, is a rather common prime factor.

      Omega-2 Divisibility Test — the base-n divisibility test applying to a factor of (n² − 1) that does not divide (n − 1) or (n + 1), involving the pairing of base-n digits beginning with the unit digit and working towards significance (meaning leftward from the radix point), then taking the digit sum of the numbers formed by these digit pairs.

Divisible — See “Divisibility”.

Division — a and b ≠ 0, written either a ÷ b = c or a/b = c. We can thus say c × b = a, as division is the inverse operation of multiplication. The number a is called the dividend, b the divisor, and c the quotient. When expressed as a/b, the expression can be interpreted as a the numerator and b the denominator of a fraction. When both a and b ≠ 0 are integers, the fraction is rational. See the MathsIsFun or MathWorld definitions.

Divisor (■■) — A number d such that k × d = n, all integers; a nonzero integer that when multiplied by another nonzero integer produces n. In this work, as a rule we refer to such numbers d as “divisors” when they divide base n, and divisors of other numbers as “factors” for clarity. (The terms “factor” and “divisor” are generally interchangeable in number theory.) See MathWorld, Prime Pages, or MathsIsFun definition.
Regarding division, the nonzero number b (not necessarily an integer) by which we divide the dividend a to yield a quotient c. In the problem 5 ÷ 2.5 = 2, the number 2.5 is the divisor. (Color canon: for the divisor 1: u, #c028c0; otherwise d, #d82028; muted: #f88890; impractical: #f8c8c8)

   Complementary Divisor — the integer d' = n/d; the factor d' by which we can multiply a divisor d to produce n.

   Distinct Prime Divisor — one of the primes p that divide n. For example, 12 = 2 × 2 × 3, so the distinct prime divisors of 12 are 2 and 3. The “little omega” function ω(n) = OEIS A001221(n) yields the number of distinct prime factors of n.

   Prime Divisor — Any prime p such that k × p = n, all integers. In this work, we generally refer to such numbers p as “prime divisors” when they divide base n, and prime divisors of other numbers as “prime factors” for clarity. (The terms “factor” and “divisor” are generally interchangeable in number theory.)

   Prime Divisors with Multiplicity — a list of the prime factors p of n whether p is repeated or not. For example, 24 = 2 × 2 × 2 × 3; there are only 2 distinct prime divisors but 4 prime divisors with multiplicity. The “big Omega” function Ω(n) = OEIS A001222(n) yields the number of prime factors of n with multiplicity.

   Proper Divisor — all divisors 1 ≤ d < n of a nonzero integer n. In other words, all divisors of n but n itself. The proper divisors of n are a subset of the proper n-regular numbers.

   Trivial Divisor — the divisors 1 and n divide all nonzero integers n; for this reason they are called “trivial divisors”. See MathWorld for the mathematical definition of the word “trivial”.

D·N·T — The analysis of the nonzero integer n in terms of integers 1 ≤ k ≤ n that are divisors (D), neutrals (N), and totatives (T). The three kinds of numbers are mutually exclusive except that 1 (see “Unit”) is both a divisor and a totative of n. We can think of “neutrals” (neutral numbers) as nondivisors in the cototient of n. This work uses the term “cardinal” to mean any 1 ≤ k ≤ n that is a divisor of n or a totative of n, i.e., a non-neutral k. Through counting functions, we determine the “predominance” of any of the three basic types of numbers 1 ≤ k ≤ n; we consider the divisor counting function τ(n) = A000005(n), neutral counting function ξ(n) = A045763(n), and Euler totient function φ(n) = A000010(n), for D, N, and T respectively. The finite set of numbers, those that have as many or more divisors than totatives, i.e., {1, 2, 3, 4, 6, 8, 10, 12, 18, 24, 30} appear in A020490. Only {2, 4, 6, 12} have more divisors than totatives; all other numbers have more totatives than divisors. The numbers that have more neutral numbers than “cardinal” {42, 54, 60, 66, 70, 72, 78, …} appear at A083244; the first odd number in this sequence is 315. We might also generate lists of the three types of numbers D, N, and T; example: for n = 10, we have divisors {1, 2, 5, 10}, totatives {1, 3, 7, 9}, and neutrals {4, 6, 8}. These lists appear in A027750, A133995, and A038566 for D, N, and T, respectively. This is the most common span-covering analysis of n on account of the long-standing familiarity with the divisor counting function and Euler totient function, their ease of computation.

The following map plots divisors in red (d ■), neutral numbers in gold (s ■), coprimes in light gray (t ■), and the number 1 which is both a divisor and coprime to n in purple (u ■). Bases n appear vertically in rows, numbers k appear horizontally. In this map, totatives only appear to the left of the zigzag line, since they are coprime numbers t < n.

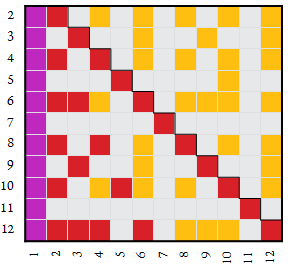
The following map shows the two species of neutral numbers, with semidivisors in orange (g ■), and semicoprimes in yellow (h ■), In this map, semitotatives and totatives only appear to the left of the zigzag line, since the former are semicoprime numbers s < n, and the latter are coprime numbers t < n.

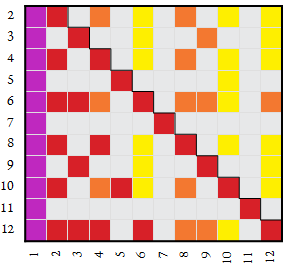
Domain — all the possible input n of a function f(n) = x is called its domain, whereas all the possible output x is called the range of the function. See MathsIsFun or MathWorld definitions.

Dozen — a grouping of twelve.

Dozenal — see “Duodecimal”.

Ducentodecimal — a number system based on 210. The number 210, a primorial, is the smallest number divisible by the smallest 4 primes (2, 3, 5, 7) and has 16 divisors {1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210}, with a record-setting RCF(210) = 68.

Dumilletrecentodecimal — a number system based on 2310.

Duodecimal — base 12 number system, also “dozenal”, rarely “duodenary”. See Mathworld or MathsIsFun definition.

Duplation — The multiplicative operation of doubling a number, used in “Russian” multiplication and in the hexadecimal roll operation. The operation is equivalent to the “roll left” function accessible on some programmers’ calculators.

E

Euler Number — e — See “Napier’s Constant”.

Euler Totient Function — φ(n) — See “Euler Totient Function”, a type of counting function.

Even — a number divisible by 2.

Evenness Test — a divisibility test that determines whether an arbitary number x is divisible by 2. In even bases, we examine the last digit to see if it is an even numeral; if so, x is divisible by 2 (i.e., even). In odd bases, we add the digits of x; if the sum is even, then x is even.

Exponent — in the expression n^ε, the number ε to which we raise n to yield a power of n. When n and ε are integers, n^ε is a perfect power and an integer as well. When we write the prime power decomposition n = p₁^e1 × p₂^e2 × … × p_k^ek, the integer exponents e represent the multiplicities of the corresponding primes. For instance, for the number 126 = 2 × 3² × 7, the multiplicity (exponent) of 3 is 2. See the MathsIsFun or MathWorld definitions.

F

Factor — A number m such that k × m = n, all integers; a nonzero integer that when multiplied by another nonzero integer produces n. In this work, as a rule we refer to such numbers m as “divisors” when they divide base n, and divisors of other numbers as “factors” for clarity. The terms “factor” and “divisor” are generally interchangeable in number theory.

   Coprime Factor — the product of all prime factors q of k semicoprime to base n that do not divide n. Consider k semicoprime to base n. Semicoprime k is composite since it is the product of at least one prime divisor p and at least one prime nondivisor q of n. Given this definition of semicoprime, we can write any semicoprime k = r × t, where the regular factor r is the product of all prime factors p that also divide n, and t the coprime factor, product of all prime factors q that do not divide n. As a consequence, the semicoprime is one of two distinct species of s neutral to n, meaning 1 < GCD(s, n) < n. The semicoprime k does not divide some perfect power of n, due to its nondivisor prime factors q. Example; 14 is semicoprime to 10 as it is the product of 2 | 10 and 7 coprime to 10; 7 is the coprime factor of 14 since GCD(7, 10) = 1.

   Distinct Prime Factor — one of the primes p that divide n. For example, 12 = 2 × 2 × 3, so the distinct prime factors of 12 are 2 and 3. The “little omega” function ω(n) = OEIS A001221(n) yields the number of distinct prime factors of n.

   Least Prime Factor (LPF) — the smallest prime divisor of n. LPF(10) = 2. See OEIS A020639.

   Neighbor Factor — a number k that divides (n − 1) or (n + 1). Neighbor factors as denominators expanded in base n have brief periods.

   Prime Factor — A prime p such that k × p = n, all integers.

   Prime Power Factor — Given the standard form prime power decomposition of the integer n = p₁^e1 × p₂^e2 × … × p_k^ek, where p₁ < p₂ < p_k, simply one of the prime powers p^e. Example: the prime power decomposition (commonly known as “factorization”) of 60 = 2² × 3 × 5, any of the terms, i.e., 2² = 4, 3, or 5, are prime powers. Since they divide 60, they are prime power factors. Certainly, 2 is also a prime power factor since 2 = 2¹, however in this work we mean one of the terms in the prime power decomposition of n.

   Regular Factor — the product of all prime factors p of k semicoprime to base n that also divide n. Consider k semicoprime to base n. Semicoprime k is composite since it is the product of at least one prime divisor p and at least one prime nondivisor q of n. Given this definition of semicoprime, we can write any semicoprime k = r × t, where the regular factor r is the product of all prime factors p that also divide n, and t the coprime factor, product of all prime factors q that do not divide n. As a consequence, the semicoprime is one of two distinct species of s neutral to n, meaning 1 < GCD(s, n) < n. The semicoprime k does not divide some perfect power of n, due to its nondivisor prime factors q. Example; 6 is semicoprime to 10 as it is the product of 2 | 10 and 3 coprime to 10; 2 is the regular factor of 6 since 2 is a divisor of 10, and a divisor is a special case of regular number.

   Greatest Prime Factor (GPF) — the largest prime divisor of n. GPF(10) = 5. See OEIS A006530.

“Factorization” — an informal term for writing the prime factors and their powers according to the standard form prime power decomposition of the integer n > 1, that is, n = p₁^e1 × p₂^e2 × … × p_k^ek, where p₁ < p₂ < p_k. See the PrimePages definition of the standard or canonical form for factorization.

Factorial — the product of the smallest n nonzero positive integers, usually written n!. {1, 2, 6, 24, 120, 720, 5040, …}. See OEIS A000142, the MathWorld, or Prime Pages definition.

Figure* — in this work, the term figure describes a component symbol of a compound numeral. In decimal-coded sexagesimalwe use in the expression of time, consider the notation “6:40” which is equivalent to the decimal 400 (i.e., 400 minutes after 12:00). The 6 and 0 are unit figures in the sixties and unit digits respectively, while the 4 is the decade figure in the unit digit. Generally we refer to upper- and lower-figures in instances outside of decimal coding (the use of base 10 to represent the digits of a large base). We might also use the term sub-rank in cases where three figures represent one digit in a very large base, numbering the ranks from the least to most significant sub-ranks. Hexadecimal with bitwise digits might be considered a binary-coded form involving 4 figures per hexadecimal digit.

   Decade Figure — in decimal-coded bases, the numeral-component that represents multiples of 10. In decimal-coded sexagesimal we use in the expression of time, we write “6:40”; in this number, which is equivalent to the decimal 400 (i.e., 400 minutes after 12:00) the 4 is the decade figure in the unit digit.

   Significant Figure — regarding scientific notation, a digit or coefficient in a real number 0 < x ≤ 1 that assures certainty in a calculation based on readings or measurements that have a level of uncertainty. This work uses the expression “significant digit” for a different notion, but significant figures are commonly also referred to as significant digits. See the MathWorld definition.

   Unit Figure — Let integer m > 1 be a sub-base or coding base and let integer n > m, m | n be the base. A symbol representing one of the integers 0 ≤ k < m in order to be used to express the least significant component of a coefficient in the alternating positional notation in base n. Example, the “narrow wedge-shaped marks” used to represent the units 1 through 9 in cuneiform sexagesimal notation.

Fivefoldness — the state of divisibility by five.

Five-smooth — a number divisible by primes that are less than or equal to 5, {1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, …}. See OEIS A051037. Also called “Hamming Numbers”.

Floor Function — a function that returns only the integer part of the number, dropping any fractional part. The floor of the number π = 3.14159… is 3. See the MathWorld or Prime Pages definition.

Fourfoldness — the state of divisibility by 4, also called “even-evenness”.

Fraction — a real number 0 < n < 1, but usually we mean a ratio of integers n and nonzero d written thus: n/d, with n the numerator and d the denominator. When n < d, the ratio is called a proper fraction. See the MathsIsFun or MathWorld definition.

   Expanded Fraction — a ratio that is converted into digital form in the positional notation of base n. For example, the ratio 7/8 expanded decimally is .875, but in octal .7, and in duodecimal .a6. In base 9, the same ratio expanded is .777….

   Fractional Part — Let n be the largest integer less than or equal to a real number x. The fractional part of x is that part k = x − n. In other words, the fractional part is the difference between the original number and its floor function. This implies that k < 1. The fractional part of 12.75 is .75. The fractional part of the number π is π − 3, which is approximately .14159265….

   Mixed Recurrent Fraction — a ratio that has an infinitely repeating periodic expansion in base n, with at least 1 non-repeating digit after the radix point. Mixed recurrent fractions pertain to ratios with denominators that are semicoprime to base. See “recurrent fraction” for examples of purely vs. mixed recurrent fractions.

   Natural Fraction — See “Natural Fraction”.

   Purely Recurrent Fraction — a ratio that has an infinitely repeating periodic expansion in base n, with no non-repeating digits. Purely recurrent fractions pertain to ratios with denominators that are coprime to base. See “recurrent fraction” for examples of purely vs. mixed recurrent fractions.

   Recurrent Fraction — a ratio that has an infinitely repeating periodic expansion in base n. Recurrent fractions are those with a nonregular denominator. Decimally, 1/12 = .08333…, 1/13 = .076923076923…, both of these are recurrent. The first example is mixed-recurrent because “08” is not recurrent (it is associated with the regular factor 4, thus includes 2 digits). The second example is purely recurrent since there are no non-repeating digits. Though we can write terminating fractions with trailing endlessly repeating 9s (e.g., 1/8 = .124999…) and thus recurrent, we do not include such fractions in this category. See the MathsIsFun or MathWorld definition. See also Hardy & Wright, Chapter IX, “The Representation of Numbers by Decimals”, Section 9.2, “Terminating and recurring decimals”, pages 141−144.

   Terminating Fraction — a ratio that has a finite number of digits to the right of the radix point when expanded in base n. Decimally, 1/2 = .5, 1/625 = .0016. In base 12, 1/3 = .4, terminating in 1 digit since 3 is a divisor. In base 14, 1/7 = .2, again terminating in 1 digit since 7 is a divisor. See MathsIsFun or MathWorld definition (pertaining to decimal only).

   Unit Fraction — a ratio whose numerator is 1.

Fractional Part — the noninteger part of a real number. Example: in the decimal number 6.25, .25 is the fractional part, also called a mantissa. See the MathWorld definition.

Function — a relationship for which there is a unique connection between elements of a domain (input) and a range (output). See the MathsIsFun or MathWorld definition.

   Boolean Function — See “Boolean Function”.

   Ceiling Function — See “Ceiling Function”.

   Counting Function — See “Counting Function”.

   Euler Totient Function — See “Euler Totient Function”.

   Floor Function — See “Floor Function”.

   Möbius Function — See “Möbius Function”.

Fundamental Theorem of Arithmetic — every positive integer n > 1 can be expressed uniquely as a product of at least one prime (excepting the rearrangement of the prime factors). The standard prime decomposition is thus n = p₁^e1 × p₂^e2 × … × p_k^ek. (We often abbreviate the formula n = Π p^ε, meaning that n is the product of prime powers.) Therefore we may express 84 = 2² × 3 × 7. See the MathsIsFun, MathWorld, or Prime Pages definitions.

G

Gradation, Step — the naming of steps or ranks of counted objects that forms a threshold. In units of time, minutes and hours are step gradations. In decimal, the ten, hundred, thousand, etc. are step gradations, the gradation being the base, 10. See Menninger, “Principles of the Number Sequence”, p. 45.

Gradus Suavitatis* — A term pertaining to harmony and pleasantness in music devised by Euler, here considered a means of extending the natural fractions and ordering denominators according to their importance. A sequence related to the gradus suavitatis function was suggested by Lamadrid 22 January 2019 as a means of discerning the importance or preference of nonzero positive integers d as denominators. For n = Π p^ε, the gradus suavitatis function GS(d) = 1 + Σ ε_k × (p_k − 1) and appears at OEIS A275314. Listing the indices of the function for a given output value (see Euler’s chart), we arrive at ({1}, {2}, {3, 4}, {6, 8}, {5, 9, 12, 16}, …). Sorted in reverse by greatest prime factor, the sequence {1, 2, 4, 3, 8, 6, 16, 12, 9, 5, 32, 24, 18, 10, …} suggests which denominators are most important. The natural fractions 1/2, 1/4, 3/4, 1/3, and 2/3 fall into this arrangement; we would then expect the odd eighths, then 1/6, 5/6, then the odd sixteenths, etc. to follow in importance. See Leonhard Euler, Tentamen novae theoriae mvsicae ex certissimis harmoniae principiis dilvcide expositae, Petropoli, ex typographia Academiae scientiarvm, 1739, page 41.

Gross — a grouping of the square of twelve or one hundred forty four; the second rank of integers expressed duodecimally.

Grouping — counting by organizing a certain number of items or objects into sets of fixed number n in order to count them. See Menninger, “Principles of the Number Sequence”, p. 39.

   Grouping of Higher Order — a grouping whose elements are also groupings. The levels of grouping are called ranks. See Menninger, “Principles of the Number Sequence”, p. 41.

Golden Ratio (Φ) — an irrational number ½(1 + √5) = 1.6180339887… that appears in the parameters of regular geometric figures involving fivefold symmetry. The number has many interesting properties, chief among them perhaps the properties Φ = 1/(Φ − 1) and Φ² − Φ − 1 = 0. See the MathsIsFun and MathWorld definitions.

Greatest Common Divisor GCD(m, n) — the largest factor that both integers m and n have. Example: GCD(10, 14) = 2, since 10 and 14 are both divisible by 2 and no larger number divides them both. We can use the GCD as a test for certain relationships. A divisor d of n has GCD(d, n) = d. A number t is coprime to n if GCD(t, n) = 1, the empty product. A number s is said to be neutral to n if 1 < GCD(s, n) < s. See MathsIsFun, MathWorld, or Prime Pages definition.

H

Hexadecimal — base 16 number system, rarely, “sedenary”, “sexadecimal”. The system is used to abbreviate binary code and to specify RGB color. See MathsIsFun or Mathworld definition.

Hexatrigesimal — a number system based on 36.

Highest Common Factor See “Greatest Common Divisor”.

Human Cognition — the capability of thought and processing data, here mostly concerned with arithmetic and calculation, by human beings. Aspects that are dependent on human cognition require scientific experimentation and empirical methods, complete with statistically-significant samples, control populations, reproducibility, etc., to assure soundness. Aspects of number bases or their use subject to the limitations or effects of human cognition suffer subjective processing or human error. Since the number base and human arithmetic are forms of human communication, the expression and interpretation of number, all the effects of human communication ascribe to writing and reading numbers. This includes interference, confusion, and unintended messages, as well as limitations imposed by the sender and receiver populations, usually presumed to be average people.

Hundred-like — in base n, the expansion of the square of n, i.e., n², written “100”. The term is used to avoid concocting nomenclature for this number. The octal hundred-like is decimal 64, while the duodecimal hundred-like is the well-known gross of 12 dozens.

A second interpretation of “hundred-like” can mean a base-n number around 100 in magnitude, as in the definition of the “greater round”.

I

Identity — an operation that yields the input number k as its result. In addition, k + 0 = k, thus 0 is the additive identity. In multiplication, k × 1 = k, thus 1 is the multiplicative identity.

   Additive Identity — addition of 0 to any number k, since k + 0 = k. See the MathsIsFun or (advanced) Mathworld definition.

   Multiplicative Identity — multiplication by 1, since k × 1 = k. See the MathsIsFun or (advanced) Mathworld definition.

Impractical — concerning regular intuitive divisibility tests, such that prove unusable due to limitations of human cognition of an average population. See Practicality.

Increment — (verb) to increase an integer k by a set amount j, usually understood to be 1. As a noun, the set amount j by which we increase an integer k. If j is understood to be 1, then incrementing k = 6 would yield k = 7. If we use j > 1, then we say “increment k by j” to clarify the number jby which we increase k.

Index — an integer that indicates the place of a value in an ordered set. Using the alphabet as an example, we say that the letter C is the third letter: its index is 3. Said of standard positional notation, an index is that exponent of the base

Indivisible — said of a number n that k does not divide evenly; k is not congruent to 0 (mod n).

Inheritor — regarding divisibility tests, a composite number k that can be factored into mutually coprime prime powers p^m such that, for each prime power, we have a divisibility test. This enables us to apply tests pertaining to each prime power factor p^m to arrive at a compound divisibility test for k. The divisibility tests for any prime power may be based on the adding of blocks of digits of the number x to be tested (neighbor tests), examination of a block of final digits (regular test), left- or right-trim tests, etc. Any composite k for which we can combine tests from prime power factors. Example: we can determine if a decimal number x is divisible by 60 since we have divisibility tests for 3 (alternating sum), 4 (regular, examinging 2 end digits), and 5 (regular, examining the last digit). We know 216,000 is divisible by 60 since 2 + 1 + 6 = 9 is clearly divisible by 3, it ends in “00”, thus is divisible by 4, and in a zero, thus is divisible by 5 (216,000 = 60³). This way, 60 is classified as an omega-inheritor, since, aside from regular prime power factors, it has an omega factor 3.

   Alpha Inheritor (h_α ■) — a necessarily composite k = r × t_α semicoprime to n such that t_α | (n + 1) and r is practical. In decimal, the number 22 is an alpha inheritor since 22 = 2 × 11; the decimal evenness test is practical, and 11 = (10 + 1). Therefore we have a workable compound divisibility test for 22 in base 10: if x is even and divisible by 11, then x is divisible by 22. The decimal number 176 is not a practical alpha inheritor. (Color canon: ha, #d0e820; impractical, hai, #e8f690)

   Alpha Omega Inheritor (h_αω ■) — a necessarily composite k = r × t_α × t_ω semicoprime to n such that t_α | (n + 1) and t_ω | (n − 1) and r is practical. In base 34, the number 30 is an alpha omega inheritor, since 30 = 2 × 3 × 5; 3 | 33, 2 | 34, and 5 | 35. Therefore we have a practical three-part compound divisibility test for 30 in base 34: if x is even and divisible by 3 and 5, then x is divisible by 30. In an odd base n, we interpret the coprime factor 2 as 2 | (n − 1) since the digit sum divisibility test is simpler. Therefore any even semicoprime also divisible by a practical regular r and a factor t_α | (n + 1) is deemed an alpha omega inheritor. In pentadecimal (base 21), 66 is an alpha omega inheritor since 2 | 20, 3 | 21, and 11 | 22. (Color canon: hb, #c8b030; impractical, hbi, #e0d880)

   Regular Inheritor —regarding intuitive divisibility tests, a composite k = r × t semicoprime to n such that the regular factor r is practical, and the coprime factor t divides a neighbor or other amenable number that is coprime to base n. The alpha, alpha-omega, omega, alpha-2, and omega-2 inheritors are regular inheritors.

   Omega Inheritor (h_ω ■) — a necessarily composite k = r × t_ω semicoprime to n such that t_ω | (n − 1) and r is practical. In decimal, the number 6 is an omega inheritor since 6 = 2 × 3; the decimal evenness test is practical, and 3 is a divisor of (10 − 1). Therefore we have a workable compound divisibility test for 6 in base 10: if x is even and divisible by 3, then x is divisible by 6. The decimal number 48 is not a practical omega inheritor. (Color canon: ho, #90c040; impractical, hoi, #c8e0a0)

Integer — a number, negative, positive, or zero, that has no fractional part: a whole number. Examples of integers include −5, 0, and 11. See the MathsIsFun or MathWorld definitions.

   Integer Length — the number of digits in a number x expanded in base n. In decimal, the number 60 has integer length 2. In binary, 60 is written “110110”, which has 6 digits, so its binary integer length is 6. The cube of the base always has integer length 4, its appearance in that base, “1000”, is thousand-like.

   Integer Part — regarding the real number x, the largest integer n ≤ x. The integer part of 6.25 is 6. The integer part of the number π is 3. We can derive the integer part using floor(x).

Interference — in communication, any environmental or intrinsic disruption of a message. Interference muddles the message or confuses the receiver.

Interpret — in communication, the decoding of a message by the receiver expressed by the sender. As regards number bases, the message decoded is a number.

Intersection — a set formed from the elements that are common to two sets. If set A includes {1, 3, 7, 9} and set B includes {1, 2, 5, 10}, the intersection of these is {1}. See MathsIsFun or MathWorld definition.

Iverson Bracket — square brackets that represent a function that return 1 if the enclosed condition is true, and 0 if false. See MathWorld definition.

J

 

K

 

L

Lamadrid Base Naming Convention — a method of furnishing standard English base names proposed by Fernando Martínez Lamadrid. The convention preserves the commonest base names like “octal”, “decimal”, “hexadecimal”, “vigesimal”, “sexagesimal” and produces names for bases b < 10,000. This standard is used in this work.

Least Common Multiple (LCM) — the smallest integer that is a multiple of at least 2 numbers. The least common multiple of 10 and 12 is 60. See the Prime Pages or MathWorld definition.

Little-endian — a method of writing terms such that the least significant comes first. In the date “4 July 1776”, the day comes before the month, which is followed by the year; this is a little-endian date format.

Logarithm — the inverse of exponentiation; for n^k, k = log_n (n^k). The logarithm to base 10 of 1000 = 3, since 10³ = 1000. The perfect power n^k has an integer logarithm k. See the MathsIsFun, MathWorld, and Prime Pages definition.

   Natural Logarithm — a logarithm based on Napier’s Constant e ≈ 2.7182818….

M

Mantissa — the fractional part of a real number. The term is usually applied to the fractional part of logarithms in base n. Note that log₁₀ 2 = 0.30103…, log₁₀ 20 = 1.30103…, log₁₀ 200 = 2.30103…; log_n 2 × 10^ε = ε + .30103…. Thus, for 1 ≤ k < n, log_n k × n^ε = ε + .M, where M is the log_nmantissa of k.

Map — See digit map.

Mediation — The multiplicative operation of halving a number, used in “Russian” multiplication, where it is actually taking the floor of half of a number, and in the hexadecimal roll operation. The operation is equivalent to the “roll right” function accessible on some programmers’ calculators.

Medium (pl: media) — in communication, a channel or space by which a message is transmitted.

Message — in communication, the intended content or subject of communication. As regards number bases, we are typically dealing with the expression and interpretation of a message that is a number.

Minuend — a number k from which we subtract m; in the expression k − m = n, k is the minuend. See MathsIsFun or MathWorld definition.

Möbius Function — μ(n) — an arithmetic function with the definition μ(n) = 0 if n has at least 1 repeated prime factor, μ(n) = 1 if n = (−1)^k, and μ(n) = 0 if n is a product of k distinct primes. A nonzero value of μ(n) indicates the number n is squarefree. See OEIS A008683; numbers with μ(n) = −1 are in A030059, those with μ(n) = 0 are in A013929, and those with μ(n) = 1 are in A030229. See MathWorld definition.

Modulo — the nonzero integer k by which we divide n to obtain a residue (remainder) r.

Multiple — the product of at least one multiplication operation. In the expression k × m = n, n is the multiple or product. If k and m are integers, then they are factors or divisors of n. See MathsIsFun or MathWorld definition.

Multiplicand — a number m which we multiply by k; in the expression k × m = n, m is the multiplicand. See MathsIsFun or MathWorld definition.

Multiplication — basically, an operation that represents the addition of a number a repeated b times. We write a × b = c with a the multiplier, b the multiplicand, and c the product. The numbers a and b are factors of c. We may write a × b = c as a · b = c or simply ab = c. Division, expressed as c ÷ b = a or c ÷ a = b, is the inverse operation of multiplication, provided the divisor (the number following ÷) is nonzero. See MathsIsFun or MathWorld definition.

   Multiplication Table — an array that shows each product of digits in the span of base n. The span is shown in the top row and leftmost column, and the products appear where the columns and rows cross. The table of products usually feature n² values, and the header rows and columns may be omitted since 1 × k = k, however, if we are dealing with values k in the span of n, then there are only (n² + n)/2 unique values. Often the decimal multiplication table involves the span 1−12, thus 78 unique values instead of 55. (See Maths Chase for an illustration of a test regarding the 12× table.) The memorization of the table presents a human cognition question regarding the difficulty of certain combinations and the length of time to memorize the table for the average student. This definition is a generalized case of the MathsIsFun or MathWorld definitions that pertain to base 10. Maths Chase demonstrates instructive decimal multiplication table facts and exercises.

   “Russian” Multiplication — a method of multiplication reliant on recursive mediation of the multiplier k and duplation of the multiplicand m. The figures are maintained in columns, which k heads the left and m the right column. In the left column, we continually mediate using the function M(k) = ⌊½k⌋ writing the result in a new row until k = 1. In the right column we double the number m in each line for as long as the mediated number k ≥ 1 in the left column. Once the table is full, we strike out all rows that have an even k then sum the remaining numbers in the right column.

An ancient variant of Russian multiplication practiced in Egypt involved transcribing the coefficients of the binary equivalent of the multiplier, then multiplying these with the multiplicand. Hence it was a reverse form of the above that proceeded from 1 to the largest perfect power of 2 that does not exceed k. The Egyptians added the numbers in the right column that corresponded with 1s in the binary expansion of the multiplier.

For more see Numberphile’s Russian Multiplication interview with Johnny Ball.

Multiplicative Complement — one of a pair of n-regular numbers k and k′whose product is some perfect power of base n. For each n-regular number k, there is a multiplicative complement k′ such that k × k′ = n^e, where integer e ≥ 0 is the richness of the regulars k and k′. The term “reciprocal” is used to mean “multiplicative complement” in the study of ancient Mesopotamian sexagesimal arithmetic. In order to reduce confusion in this work we refrain from this definition and instead use the term “multiplicative complement”.

Multiplicity — in this work, multiplicity refers to the power of a particular prime divisor p of n. For 60 = 2² × 3 × 5, the multiplicity of the prime 2 is 2, while the multiplicities of the other prime divisors is 1.

Multiplicity Notation* — MN(n) — a function that writes the exponents e of the prime factors p of n in the π(p)-th place. Example: 84 = 2² × 3 × 7: the multiplicity notation that represents 84 is “1012”. See OEIS A054841, where it is known as “Exponential Prime Power Representation” per W. Nissen. Used here, we express MN(n) in a bigendian way, with the largest prime's exponent in the leftmost place, reversing A054841. Multiplicity notation is an abbreviation of prime decomposition for numbers that are products of many small primes.

Multiplier — a number k by which a second number n is multiplied; in the expression k × m = n, k is the multiplier. See MathsIsFun or MathWorld definition.

Multus* (■) — a composite prime power, such as 4, 27, or 125. These numbers are listed in OEIS A246547. The color code for multus numbers is gold. The name is a coinage of 2022, deriving from Latin multus, meaning “many”, as there are many copies of the same prime producing such numbers. In terms of OEIS, A246547 = A246655 \ A40, that is, prime powers without primes themselves. The product of multiple multus numbers is a sort of tantus number called a plenus number.

Myriad — Greek word for the number 10,000. The term is used as a shorthand for English “ten thousand”. See “MathWorld” definition.

Myriad-like — in base n, the expansion of n⁴, written “10000”. The term is used to avoid concocting nomenclature for this number.

N

Napier’s Constant — e — the base of the natural logarithm, e.g., decimal 2.718281828….

Natural fraction — one of the set of fractions most commonly used by humanity, across cultures, and throughout history. The set specifically includes 1/2, 1/4, 3/4, 1/3, and 2/3.

Neighbor — the integer n ± 1. In this work we call α = (n + 1) the alpha number, and ω = (n − 1) the omega number, as these have special properties when written in integer base n.

   Neighbor Factor — See “Neighbor Factor”.

   Neighbor, Perfect Power — A factor of n^ε ± 1. Consider ω = (n − 1), the omega number; factors t_ω | ω are coprime to n, but are minimally recurrent, with period 1. Similarly, α = (n + 1) the alpha number has factors t_α | α are coprime to n, but are semiminimally recurrent with period 2. Therefore, the omega number as denominator has a purely recurrent expansion in base n that involves a single repeating digit, while the alpha number involves 2 repeating digits. A decimal example of omega is 1/3 = .111… and 1/11 = .090909…. Furthermore, the omega enjoys the digit sum divisibility test while the alpha has the alternating sum divisibility test. On account of these simple relations, we recognize the neighbor factors as tools in base n, especially when these neighbors are highly factorable and infill primes that interpose among the prime divisors of n. We can continue with the omega-2 factors t_ω2, those factors that divide (n² − 1) but neither (n − 1) nor (n + 1); these enjoy the paired-digit sum divisibility test. Similarly, the alpha-2 factors t_α2, those factors that divide (n² + 1) that enjoy the paired-digit alternating divisibility test. Decimally these apply to the numbers 33 and 101 respectively and thus are obscure. Certain numbers can employ these perfect power neighbors to derive methods that furnish divisibility tests for their factors. For instance, in base 12, the number 5 is a long prime practically as opaque in that base as 7 is decimally. Since 5 | (12² + 1), we can determine an arbitrary duodecimal number x is divisible by 5 by splitting x into pairs of digits (units and dozens, grosses and great grosses, etc.) then taking the alternate sum. Example: duodecimal “5954” is divisible by 5 since “59” − “54” = 5 and 5 is clearly divisible by 5 (duodecimal “5954” = decimal 10,000).

Neutral* (adjective) (s ■) — a nondivisor k that is not coprime to base n. Neutral numbers k are indicated by 1 < gcd(k, n) < k. The neutral number is implicitly composite since a prime must either divide n or be coprime to it. There are two species of neutral number: a semidivisor is a number k that divides some perfect power of n greater than base n itself, and a semicoprime that is a number k that does not divide any integer power of n and is not coprime to n. The number of neutral numbers ξ < n is given by the neutral counting function ξ(n) = n − (τ(n) + φ(n) − 1), where τ(n) is the number of divisors of n, and φ(n) is the number of totatives of n. (Color canon: s, #ffc010)

Noise — See “Interference”.

Nomenclature — the words we use to express a number in written and spoken language. See Menninger and Ifrah for extensive analysis of nomenclature. In English, we have a rudimentary nomenclature for base 12. For instance, the dozen, gross, and great gross are the first three ranks of a duodecimal base. We might use the English words for the numerals 0 through 11 as they are, and thus write a sentence like “seven times ten is five dozen ten” or say “three dozen divided by six is six” and be fully understood by any native English speaker.

Nonary — the number system based on 9, sometimes called “enneal”.

Noncoprime — a number k that has some common prime factor with n, both nonzero integers. (i.e., nonzero integers k and n such that GCD(k, n) > 1). Regular and semicoprime numbers are noncoprime to n (except 1, both regular and coprime to n). If a number k has at least one prime factor in common with n, it is noncoprime.

Nondecimal — not pertaining to the number 10. Usually referring to a number base that is not based on 10. Hexadecimal and binary are nondecimal bases.

Nondivisor — for k and n, integers, the ratio n/k is not an integer. Example: 4 is a nondivisor of 10. All numbers greater than 10 are nondivisors.

Nonregular — a number k that does not divide any power n^e, integers. Such a number k as denominator of a fraction has a recurrent expansion in base n. See MathWorld definition (their definition pertains to base 10; this is a generalized definition).

Nontrine (adjective) — a number not divisible by three, i.e., x is not congruent to 0 (mod 3).

Nonzero — a number that is not zero. This constraint is usually in place to avoid division by zero. See MathWorld definition.

Notation — a manner of communication complete with rules for transmitting numbers, operations, and other messages between sender and receiver.

   Positional Notation — See “Positional Notation”.

   Scientific Notation — the expression of a large number x in base n using the j most-significant digits of x (that is, j significant figures) as k × n^ε where k is a coefficient 1 ≤ k < n. For example, c the constant speed of light is 299,792,458 m/s. We might only be interested in 3 significant figures, so we write c = 3.00 × 10⁸ m/s, the trailing zeros used to maintain the number of significant figures in the constant.

Null — an empty value.

Number — in this work, we typically mean “integer” when we write “number”, that is, the result of counting items and the number zero. Generally defined, a number is a member of a possibly ordered set which might include numbers that are rational but not integer, positive, negative, real, complex, transcendental, or some other constant. We are mostly concerned with the representation of real numbers by expression in the standard positional notation of an integer base n. See the MathWorld definition.

   Irrational Number — a number that cannot be expressed as a ratio. Such numbers expanded in any base neither terminate nor are periodic. See the MathsIsFun or Mathworld definition.

   Number Base — See “Base”.

   Number System — a form of communication that is a means of representing numbers; a method used to express numbers. Tally, Roman numerals, and positional notation based on a number base n are all number systems. Sometimes we say “base n number system”, meaning some form of representing arbitrary numbers with respect to the number n.

   Number Theory — A branch of mathematics, sometimes called “higher arithmetic”, that primarily deals with the properties of integers (e.g., primality, divisibility, partitions) and their relationships (e.g., multiplicative relationships, greatest common divisors, squarefree kernels, etc.). Number theory governs the mechanics of a number base, though the expression of numbers in a base and the interpretation and manipulation of the expressions by human beings is a form of communication and the province of human cognition. See the MathWorld definition, or HowStuffWorks. A great, succinct, but advanced description appears at Stanford. See this link for “things of interest to number theorists”.

   Rational Number — See “Ratio”.

   Real Number — a number that may be an integer, positive, negative, or 0, or any number with a nonzero fractional part. The following decimal numbers are real: −5.333…, 0, 4, 375-½. Numbers that are not real are imaginary, that is, of the form a + bi, with i = √−1. See the MathsIsFun or MathWorld definition.

   Transcendental Number — a necessarily irrational number that cannot be produced using algebra. The numbers π and e are transcendental. See the PrimePages or MathWorld definitions.

Numeral — a symbol, written or spoken, that represents a number. See Mathworld definition, also see Menninger. In general we assign numerals to all integers 0 ≤ k < n to represent place values in the standard positional notation of an arbitrary number x expressed in base n.

   Alphanumeric Numeral* — one of the set of numerals that borrows transdecimal numerals from the English alphabet {a, b, c, …, z} and appends these to the set of Hindu Arabic numerals to represent transdecimal digits {10, 11, 12, …, 35}, respectively. Further, the uppercase letters may likewise be appended either in place of or along with the lowercase. The marshaling of letters to behave as numerals renders them unavailable for variables, or at least introduces confusion. Some letterforms, such as uppercase-I, lowercase-l, conflict with the numeral 1. Commonly, hexadecimal is represented using alphanumeric numerals, using lower or uppercase A through F for digits 10 through 15 respectively.

   Bitwise Numeral* — a numeral that visually portrays the binary digits of a number. Bruce Martin’s 1968 proposal for hexadecimal numerals is a clear example of bitwise numerals.

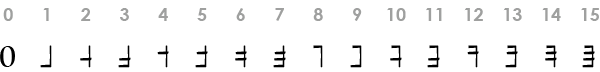
   Compound Numeral* — a symbol composed of more than one component or figure that together represent a place value in the alternating positional notation of an arbitrary number x expressed in base n. Example, the decade figure and unit figure of cuneiform sexagesimal numerals together constitute a compound numeral.

   Cuneiform Numeral — a symbol representing a number, wedge-shaped due to being impressed into a soft medium by a stylus or reed. The Mesopotamian sexagesimal number system used cuneiform numerals.

   Hindu-Arabic Numeral (HAN) —One of the set of decimal numerals used in today’s numbers: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} just as they appear and are commonly written.

   Natural Numeral* — Strictly, a symbol, written or spoken, representing any positive or negative real number in order to be used to express place values in the standard positional notation in base n. The term is equivalent to “proper numeral” when this term pertains to a positive integer base. It also includes components of compound numerals in bases expressed in alternating positional notation.

   Proper Numeral* — Strictly, a numeral representing one of the integers 0 ≤ k < n in order to be used to express place values in the standard positional notation in base n. In decimal, these are the integers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, represented here in the Hindu Arabic numerals, but any similar decimal system of numerals constitute a system of proper numerals.

   Quasi-numeral — See “Quasi-numeral”.

   Transdecimal Numeral* —A term this work uses for any numeral that represent digits k > 9, used in bases n > 10.

Numerator — in a ratio n/d, integers, d ≠ 0, the number n is the numerator. See MathsIsFun or MathWorld definition.

O

Octal — base 8 number system, rarely “octonary”, “octonal”, “octimal”, “octaval”. See Mathworld definition.

Octodecimal — a number system based on 18.

Octoquadragesimal — a number system based on 48.

Odd — a number not divisible by 2.

OEIS — the On-Line Encyclopedia of Integer Sequences, a curated and peer-reviewed internet repository for integer sequences of interest to professional and amateur mathematicians. The OEIS is referenced in this work in order to direct readers to a standard database complete with further references and links that may yield more information about certain kinds of numbers discussed herein. (Disclosure: the author of this work is an associate editor at OEIS. This work and the OEIS are not functionally related, however, and no claim herein necessarily constitutes a claim made by the OEIS.)

Omega (Functions) — ω(n) or Ω(n) — these functions render the number of prime divisors of an integer. See immediately below.

   Big Omega — Ω(n) — the number of prime factors of n with multiplicity. Example: the prime factors of 12 are 2 × 2 × 3, thus Ω(12) = 3. See OEIS A001222.

   Little Omega — ω(n) — the number of distinct prime divisors of n. Example: the prime factors of 12 are 2 × 2 × 3, but there are only 2 distinct primes, {2, 3}. Thus ω(12) = 2. See OEIS A001221.

Omega-Multiplicity Diagram* — a partition of the natural numbers ℕ by the number of distinct prime divisors ω(n) and the maximum multiplicity M(n) of a number n. The number 1 is the empty product and is in a category of its own. Prime numbers (■) have ω(n) = M(n) = 1 and appear in OEIS A40. Varius numbers (■) are composite squarefree numbers with ω(n) = 1 but M(n) > 1 and appear in OEIS A120944. Multus numbers (■) are composite prime powers with ω(n) > 1 but M(n) = 1 and appear in OEIS A246547. Finally, tantus numbers (■) are composite numbers that are neither squarefree nor prime powers with both ω(n) and M(n) exceeding 1, and are listed in OEIS A126706. The names of the several novel species of number are coinages of early May 2022.

Omega-Multiplicity Diagram

	M(n) = 1	M(n) > 1
ω(n) > 1	■ multus	■ tantus
ω(n) = 1	■ prime	■ varius

Omega (Number) (ω ■, enhanced ■) — regarding base n, the number (n − 1). In base 10, ω = 9. Omega is coprime to base, but has minimal period. Therefore omega or any of its factors in the denominator has a 1-digit purely recurrent expansion in base n. In decimal, 1/3 = .333…, and 1/9 = .111…. In hexadecimal, 1/3 = .555…, 1/5 = .333…, and 1/f = .111…. Base n divisibility tests for omega involve adding the digits of x. If the sum is divisible by ω, then so is x. Decimally, 729 is divisible by 3 since 7 + 2 + 9 = 18 is divisible by 3; likewise it is also divisible by 9. Note: this omega ought not be confused with the omega functions. (Color canon: to, #c8dee8, enhanced: too, #00c070)

   Omega Factor (t_ω ■, enhanced ■) — a divisor of the omega number; for base n, a factor of the number (n − 1), to which the properties of the omega number also ascribe. (Color canon: to, #c8dee8, enhanced: too, #00c070)

Omega Test — See “Omega Divisibility Test”.

Opacity* — the state of a nonregular number indivisible by a neighbor factor, thus having no intuitive divisibility test. Decimally, the nonregular 3 is not opaque, since it is a neighbor factor (i.e., of 10 − 1 = 9). Therefore 6 = 2 × 3, product of a regular and a neighbor factor (thus an omega-semitotative) has a compound divisibility test: if a number is even and divisible by 3, it is divisible by 6. In base 12, the number 5 is opaque, since it is not a neighbor factor or a divisor of 12. Therefore the number ten = 2 × 5, product of a regular and an opaque totative, is an opaque semitotative.

Opaque* — said of an integer k > 1 for which there are no practical intuitive divisibility tests. Any number that does not have a regular or neighbor-factor divisibility test or combination thereof is said to be “opaque” in base n. Regarding the positive integers 2 ≤ k ≤ n, the numbers {2, 4, 5, 8, 10} are regular to 10, but the decimal regular divisibility test for 8 involves 125 3-digit combinations and is not practical. The numbers 3 and 9 divide a neighbor of 10 (i.e., 9). The number 6 = 2 × 3, a product of a regular and a neighbor-factor of 10. Therefore 7 and 8 are opaque in base 10. The alpha-2 and omega-2 divisibility tests, as well as the left- and right-trim tests are considered “non-intuitive” and show as opaque. In certain bases, such “non-intuitive” tests would indeed prove fairly useful when they apply to small, often-used factors scuh as 5 or perhaps 7.

Operation — an arithmetic process or function, the most common of which are addition, subtraction, multiplication, division, and exponentiation. See the MathsIsFun or MathWorld definition.

Overtrine (adjective) — a number one more than a multiple of 3, i.e., 3x + 1, or a number congruent to 1 (mod 3).

P

Parity — the relationship of integer x with the number 2, i.e., either even or odd. See MathWorld or MathsIsFun definition, or test your mettle regarding decimal odds and evens with a simple game at Maths Chase.

Partition — any combination of nonzero positive integers that when summed yield an integer n. Basically the partitions of n are “all the unique ways we can make n through addition of positive integers”. Conventionally these integers are ordered from greatest to least. The partitions of 5 are (5), (4, 1), (3, 2), (3, 1, 1), (2, 2, 1), (2, 1, 1, 1), and (1, 1, 1, 1, 1). The numbers that appear in a partition are called “parts”. The partition function P(n) yields the number of (unrestricted) partitions an integer n possesses. A partition can be charted, the charts called Young or Ferrers diagrams. See the MathWorld definition for more detail. We normally refer to “additive partitions” when partitions are discussed, but “multiplicative partitions” are any combination of integers k > 1 that produce an integer n. The multiplicative partitions of n can be thought of as “all the unique ways we can make n through multiplication of positive integers larger than 1”. For instance, we can produce 12 in four unique ways: (1 ×) 12 = 2 × 2 × 3 = 2 × 6 = 3 × 4. See the OEIS Wiki for more.

Pentadecimal — the number system based on 15, sometimes called “quindenary” or “quindecimal”.

Percent — parts per hundred, usually followed by the symbol “%”. The fraction 1/8 = 12.5%.

Pergrade — parts per 120, expressed in decimal-coded centovigesimal, usually followed by the symbol “p/g”. The fraction 1/9 = 13;40 p/g (i.e., 13 1/3 pergrade). Pergrade is useful since many denominators are regular (thus terminate) or neighbor-factors with respect to 120.

Period (Recurrent) — λ — The number λ of repeating digits or reptend in a recurrent fraction expressed in base n. See the Prime Pages definition.

   Maximum (Recurrent Period) — A term used in this work that describes the length λ_t = (q − 1) of a reptend m for a denominator q coprime to base n. The base-n expansion of a fraction with q in the denominator can only involve at most λ_t = (q − 1) places. The maximum recurrent period is sometimes the commonest period for prime q across bases n. Other sources have the term “long prime” for a q that has the maximum period λ_t = (q − 1) in base n. A decimal example of a long prime is 7; 1/7 = .142857…, a 6-place mantissa. (Color canon: tpp, #bfc0c1)

   Semimaximum (Recurrent Period) — A term used in this work that describes the length λ_t = ½(q − 1) of a reptend m for a denominator q coprime to base n. The term “semimaximum” is used because λ_t = ½(q − 1) is the longest period possible outside of the maximum period λ_t = (q − 1), and is nearly as or as common as the maximum for prime q across bases n. A decimal example of a prime with a semimaximum period is 13; 1/13 = .076923…, a 6-place mantissa. (Color canon: tp, #d7d8d9)

   Intermediate (Recurrent Period) (t ■) — A term used in this work that describes the length 2 < λ_t < ½(q − 1) of a reptend m for a denominator q coprime to base n. The intermediate period is possible if and only if (q − 1) has more than 4 integer divisors. A decimal example of a prime with an intermediate period is 37; 1/37 = .027027…, a 3-place mantissa. (Color canon: t, #e8e9ea)

   Semiminimum (Recurrent Period) (t_α ■) — A term used in this work that describes the length λ_t = 2 of a reptend m for a denominator q coprime to base n. The semiminimum period λ_t = 2 belongs to the alpha number α = (n + 1) and its integer factors t_α. The term “semiminimum” is used because λ_t = 2 is the smallest period possible outside of the minimum period λ_t = 1. (Color canon: ta, #c8dcb2, enhanced: taa, #00aaa0)

   Minimum (Recurrent Period) (t_ω ■) — A term used in this work that describes the length λ_t = 1 of a reptend m for a denominator q coprime to base n. The minimum period λ_t = 1 belongs to the omega totative ω = (n − 1) and its integer factors t_ω. The base-r expansion of a fraction with q in the denominator must involve at least λ_t = 1 places. A decimal example of digits with the minimum recurrent period is 1/3 = .333… and 1/9 = .111…, single-place mantissae. (Color canon: to, #c8dee8, enhanced: too, #0070c0)

Pi-Code (or π-code) — the first differences of the indices of the prime factors of n with multiplicity, sorted least to greatest. For example, 360 = 2³ × 3² × 5 = 2 · 2 · 2 · 3 · 3 · 5. Since the index of 2 = 1 (it is the first prime), the index of 3 = 2 (the second), etc., we write 1,1,1,2,2,3 and the differences, starting with the first number in this list, are 1,0,0,1,0,1. Thus, the π-code is “100101”. Pi-code aids in studying the prime decomposition of squarefree or moderately powerful numbers that are the product of many primes.

Place — In the standard positional notation of base n, a location in a string of digits that represents a perfect power n^ε, where ε represents the index of the place. A digit k in the ε-th place is the coefficient of the power n^ε and has the value kn^ε. Example: in the decimal number “789.25”, there is a 7 in a place that has the value 10³, thus 7 in that position signifies 7 × 10³ = 7000. We say that 7 is in the “hundreds place”.

   Hundreds Place —In decimal standard positional notation, the third digit from the right in an integer, representing k × 10², with an integer coefficient 1 ≤ k < 10. The hundreds place has index 2, therefore consitutes the second decimal rank. In the decimal number “1975”, the number 9 appears in the hundreds place. In other number systems we might speak of “hundred-like”places through analogy with base ten.

   Hundredths Place — In the decimal expansion of a fraction, rational or irrational, the second place to the right of the decimal point. In the decimal number 6.875, the 7 appears in the hundredths place.

   Place Value — the perfect power n^ε that pertains to a place in the positional notation of base n. The digit that appears in the place is called the coefficient. Example: in the decimal number “789.25”, the number 8 is in the tens place; the place value at the number 8 is ten, and at the 7 is hundred, whereas the 8 is the coefficient in the tens place. When we read the number 789.25, we think of the equation 7 × 10² + 8 × 10¹ + 9 × 10⁰ + 2 × 10⁻¹ + 5 × 10⁻², products of coefficients and perfect powers of the base. See MathsIsFun definition, or play the simple game at Maths Chase.

   Tens Place — In decimal standard positional notation, the second digit from the right in an integer, representing k × 10¹, with an integer coefficient 1 ≤ k < 10. The tens place has index 1, therefore constitutes the first decimal rank. In the decimal number “1975”, the number 7 appears in the tens place.

   Tenths Place — In the decimal expansion of a fraction, rational or irrational, the first place immediately to the right of the decimal point. In the decimal number 6.875, the 8 appears in the tenths place.

   Thousands Place — Regarding decimal standard positional notation, the digit third from the right in an integer, representing k × 10³, with an integer coefficient 1 ≤ k < 10. The thousands place has index 3, therefore constitutes the third decimal rank. In the decimal number “1975”, the number 1 appears in the thousands place. In other number systems we might speak of “thousand-like” places through analogy with base ten.

   Thousandths Place — In the decimal expansion of a fraction, rational or irrational, the third place to the right of the decimal point. In the decimal number 6.875, the 5 appears in the thousandths place.

   Units Place — In decimal standard positional notation, the rightmost digit in an integer or immediately to the left of the decimal point, representing k × 10⁰, with an integer coefficient 1 ≤ k < 10. The units place has index 0, and is sometimes called the ones place. In the decimal number “1975”, the number 5 appears in the units place.

Plenus* (■) — a composite number n that is the product of more than 1 composite prime power. Examples include 36 = 2² × 3², 72 = 2³ × 3², and 225 = 15² = 3² × 5². Indeed all powers of squarefree semiprimes (outside of the semiprimes themselves) are plenus numbers. Powers (greater than 1) of a varius number are plenus. For plenus numbers n, we have multiple distinct prime divisors p, where p | n implies p² | n. These numbers are listed in OEIS A286708. Plenus numbers are also tantus numbers; the are a special case, hence A286708 ⊂ A126706. Likewise, plenus numbers are related to multus numbers (A246547), since the prime power factors of a plenus number are multus numbers. Indeed, A286706 = A1694 \ A961 = A1694 ∪ A24619; that is, plenus numbers are a subset of powerful numbers; they are powerful numbers that are not prime powers. The color code for plenus numbers is magenta. The name is a coinage of June 2022, from Latin plenus meaning full, satisfied, or plump, since n is a product of more than 1 prime power whose exponent exceeds 1.

Positional Notation — a means of expressing a number x = k₁ n^i_1 + k₂ n^i_2 + k₃ n^i_3 + k₃ n^i_4… with indices i₁ > i₂ > i₃ > i₄ … and generally with all the coefficients k positive integers less than n in base n as “k₁k₂k₃k₄…”, that is, writing only the coefficients k of each perfect power of the base in a position or place nⁱ corresponding to their index i. In decimal standard positional notation, the places, starting from the decimal point, pertain to ones (or units), tens (10¹), hundreds (10²), thousands (10³), etc., thus the decimal number “1234” has 1 in the thousands, 2 in the hundreds, etc., in a bigendian manner. The decimal “1234” = 1 × 10³ + 2 × 10² + 3 × 10¹ + 4 × 10⁰ = 1000 + 200 + 30 + 4. We might write a number instead to base n = 12. Then the places would pertain to units, dozens (12¹), grosses (12²), great grosses (12³), etc. In this case the same expression, interpreted in dozenal, “1234” = 1 × 12³ + 2 × 12² + 3 × 12¹ + 4 × 12⁰ = 1 × 1728 + 2 × 144 + 3 × 12 + 4 = 1728 + 288 + 36 + 4 = decimal 2056. We might also write a number in a non-standard way, such as little-endian, where the smallest places appear on the left, thus “321” meaning one hundred twenty three, or in a “balanced” way, where we can have negative coefficients, etc.

   Standard Positional Notation — The expression of a number using positional notation in which the coefficients k are integers 1 ≤ k < n and the places are in bigendian order.

Power — an exponent ε to which a number n is raised, normally shown in superscript on the right of a number: n^ε. Supposing n and ε are integers, ε represents the number of times we multiply n with itself. Thus, 2³ = 2 × 2 × 2 = 8. Also, integers n^ε that are the result of raising n to the ε-th power. The logarithm of x to base n (written log_n x) yields the exponent ε to which ε is raised to yield x. Thus, log₂ 8 = 3. For numbers x that are not perfect powers of n, ε is not an integer. See Mathworld or MathsIsFun definition.

   Perfect Power — An integer that results from raising n to the e-th power, both integers. 100 is a perfect power of 10 since it is 10². This phrase is often simply “power”. See Mathworld definition.

   Prime Power — See “Prime Power”.

Powerful Number — a number n whose prime divisors p have multiplicity ε > 1. *** See OEIS A001694 or the MathWorld definition.

Practicality — the ability to reliably use a divisibility rule or arithmetic method. Practicality indicates the limitation of human cognition in taking advantage of a number-theoretic property of base n and its relationship with a number k. For example, the decimal evenness test is practical: a number is even if it ends in one of 5 digits: {0, 2, 4, 6, 8}. The rule is simple enough for a small child to master. The decimal intuitive divisibility test for divisibility by 8 is impractical: we must compare the last three digits of an arbitrary number x with one of 125 possible 3-digit combinations {000, 008, 016, 024, …, 992}. This test can be made practical via range folding, but there is a point beyond which the regular test is irrecovably impractical. An evenness test in a sufficiently large base can also prove impractical, as there are too many even digits to memorize.

Primality — of or having to do with prime numbers. A primality test is a method of determining whether a number is prime. Prime sieves are a common method of determining whether a relatively small number is prime. One of the simplest sieves perhaps is the evenness test: we know the only even prime is 2, thus any larger even number is composite, yet all odd numbers are not prime, and we will need to do more work to determine primality. Such tests become difficult as the magnitude of the prime-candidate increases. In these cases one may attempt to obtain a prime certificate. See PrimePages for more.

Prime — An integer p that has two divisors, 1 and p is prime. Every integer n > 1 is the product of one or more primes p. A prime p either divides a number p or is coprime to it. If a prime p divides n, it must divide one of its factors k. The number 1 is not prime by definition. See OEIS A000040, MathsIsFun, Mathworld, or Prime Pages definition. Take a look at the Prime Pages for in-depth information on primes. Maths Chase has a simple game that tests recognition of prime numbers expressed decimally.

   Even Prime — The number 2 is the only even prime. All greater even numbers are multiples 2k and composite.

   Long Prime — (or “full period prime”) A prime p such that the unit fraction 1/p, expanded in base n, has period (p − 1). The number 7 in base 10 is a long prime, since 1/7 = .142857142857…, the reptend “142857” has 6 digits. See the MathWorld or Prime Pages definition.

   Odd Prime — All primes k > 2 are odd; any prime except 2.

   Prime Power — See “Prime Power”.

   Prime Sieve — See “Prime Sieve”.

   Prime Signature — See “Prime Signature”.

   “Prime to …” — See “Coprime”.

   Relatively Prime — See “Coprime”.

   (Generalized) Wieferich Prime — See “Wieferich Prime”.

Prime Power — a real number p^e with p prime and integer e > 0. The number 16 is a prime power since it is 2⁴. See OEIS A000961 or the MathWorld definition. The OEIS lists prime powers in A961 along with the empty product 1. The prime powers appear in A246655 without 1. Multus numbers are composite prime powers, listed in OEIS A246547, with only one distinct prime divisor and multiplicity greater than 1. Therefore, in terms of OEIS, A246547 = A961 \ ({1} ∪ A40) = A246655 \ A40.

Prime Sieve — (the Sieve of Eratosthenes) a method of determining which numbers on a list of the smallest numbers are prime. See the interactive MathsIsFun activity or PrimePages (spoiler alert for the MathsIsFun activity!) for more.

Prime Signature — a list of nonzero multiplicities of the distinct prime factors of n, usually sorted greatest to least. The number 8 = 2³, so its prime signature is {3}; the number 24 = 2³ × 3, its prime signature is {3,1}. The number 420 = 2³ × 3² × 7, and the number 360 = 2³ × 3² × 5, but these numbers both have the same prime signature {3,2,1}. See OEIS A118914 for a list sorted least to greatest, and A025487 for a list of the smallest numbers with a given prime signature {1, 2, 4, 6, 8, 12, 16, 24, 30, 32, 36, …}. See the MathWorld definition.

Primorial — a product of the smallest n prime numbers p: {1, 2, 6, 30, 210, 2310, 30030, …} (1 is in the sequence since it is the empty product). See OEIS A002110, definitions in MathWorld or Prime Pages.

Product — the result of at least one multiplication operation, e.g., 2 × 3 = 6; 6 is the product. See MathsIsFun or MathWorld definitions.

   Empty Product — since 1 times any number n yields n (the multiplicative identity), 1 is considered multiplicatively empty; it is the empty product. It is a number that is not the product of any number of primes.

   Unique Product — a combination of multiplier and multiplicand k × n and its conjugate n × k which yield the same product. For instance the numbers 4 × 7 and 7 × 4 in the decimal multiplication table both pertain to the same “unique product”, 28. Though (3 × 4, 4 × 3) and (2 × 6, 6 × 2) have the same product 12, we have two distinct unique products. The number of unique products in a multiplication table is (n² + n)/2 for base n

Q

Quadratfrei — See “Squarefree”.

Quarter — one fourth, 1 of 4 equal divisions of a whole.

Quaternary — having to do with 4, fourfold; also the number system based on 4.

Quinary — having to do with five, fivefold; also the number system based on 5.

Quinmillequadragesimal — a number system based on 5040.

Quasi-numeral* — a group of numerals that serve as surrogates signifying a number other than the strict interpretation of the numerals. Example: decimal “25” is a quasi-numeral that means “one quarter (of a hundred)”.

R

Radix — See “Base”.

Radix Point (Adjective) — a symbol, in the United States usually a period (full stop, “.”) and in Europe a comma (“,”), that demarcates the integer part from the fractional part of a number represented in standard positional notation in base b. The decimal point or simply “decimal” is used in base ten. In this work we use the base-neutral term “radix point” for numbers in all bases other than decimal. See Prime Pages.

Radical (function) — rad(n) — See “Squarefree Kernel”.

Range Folding — concerning regular intuitive divisibility tests, the performance of a simpler test on a digit more than 1 digit from the right to alleviate the number of combinations that may contain the final digits of an arbitrary number. Example: consider the decimal divisibility test for 8. “An arbitrary integer x is divisible by 8 if the last 3 digits of x match one of 125 three-digit combinations {000, 008, 016, 024, …, 992}”. It is conceivable that memorizing 125 three digit combinations is out of reach for most people. We can simplify the rule by applying an evenness test on the 3rd digit from the right. This way the rule becomes “An arbitrary integer x is divisible by 8 if the 3rd digit from right is even and the last 2 are one of 13 two-digit combinations {00, 08, 16, 24, …, 92}, or the 3rd digit from right is odd and the last 2 are one of 12 two-digit combinations {04, 12, 20, 28, …, 96}”.

Rank (Positional Notation) — the power of base n that pertains to the place. In the decimal number 123, the numeral 2 is in the second rank, while 3 is in the first rank.

Ratio — integers n and d written either n:d or n/d, with n the numerator and d ≠ 0 the denominator, also commonly called a fraction. Carrying out division of n/d, we obtain a quotient, thus a quotient and a ratio, when are integers, is the same thing. A number that is a ratio is said to be “rational”, while number that cannot be expressed as n/d with integers, are called “irrational”. See the MathsIsFun, PrimePages, or MathWorld definition.

Receiver — The audience (intended or unintended) of communication; someone who senses a message, usually someone to whom the message was sent by the sender.

Reciprocal — the multiplicative inverse of n = n⁻¹. The reciprocal of a fraction a/b = b/a. See MathsIsFun or Mathworld definition. The term “reciprocal” has a second definition pertaining to the study of Mesopotamian sexagesimal arithmetic, see “multiplicative complement”.

Reciprocal Divisor Method — See “Multiplicatively Complementary Factor Method”. ***

Records Index — regarding a function f(n) that generates a sequence of numbers that generally increases, the places where values in that sequence that set records as n increases. For instance, the divisor counting function τ(n) over the range 1 ≤ n ≤ 12 is {1, 2, 2, 3, 2, 4, 2, 4, 3, 4, 2, 6}; the records transform is {1, 2, 3, 4, 6} (i.e., OEIS A002183). The indices of the records are {1, 2, 4, 6, 12} (i.e., the highly composite numbers, OEIS A002182). The records transform is useful in attempting to maximize a function while economizing the input. See MathWorld definition.

Records Transform — regarding a function f(n) that generates a sequence of numbers that generally increases, the values in that sequence that set records as n increases. For instance, the divisor counting function τ(n) over the range 1 ≤ n ≤ 12 is {1, 2, 2, 3, 2, 4, 2, 4, 3, 4, 2, 6}; the records transform is {1, 2, 3, 4, 6} (i.e., OEIS A002183). The indices of the records are {1, 2, 4, 6, 12} (i.e., the highly composite numbers, OEIS A002182). The records transform is useful in attempting to maximize a function while economizing the input. See MathWorld definition.

Recurrent (Adjective) — repeating or cyclical.

Regular (Adjective) — a nonzero number k that divides some perfect power of base n, i.e., k | n^ε with ε ≥ 0, integers. Also, a number k that is not divisible by nondivisors of n. Divisors d are a special case of n-regular number such that d | n^ε with integer 0 ≤ ε ≤ 1. Example: in decimal, the regular numbers are any multiple of the perfect powers of 2 or 5, i.e., {1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, …}. Among these are the divisors of 10, {1, 2, 5, 10}. The smallest exponent ε such that regular k | n^e is known as the richness of regular k. Regular numbers k as denominators m/k enjoy terminating expansions in base n; the number of digits right of the radix point is equivalent to the richness e. Example: 8 is regular to 10, thus in decimal 1/8 has three digits to the right of the decimal point (1/8 = .125). The regular divisibility test involves examining the last ε digits of the number x to see if it is one of n^ε/k combinations. Example: in base 10, to see if a number is divisible by 4, we examine the last 2 digits. If the number formed by these digits is one of {00, 04, 08, 12, 16, …, 96} (25 combinations), it is divisible by 4. The regular relationship is one of the three constitutive arithmetic relationships.

   Primitive Regular — A proper regular R in base n is a regular number r | n^εsuch that LCM(n, r) ≠ r. See “Proper Regular”.

   Proper Regular — in base n, an n-regular r that does not have trailing zeros when expressed in base n. In other words, an n-regular r that is not a multiple of base n. A proper regular R in base n is a regular number r such that LCM(n, r) ≠ r. The proper divisors of n are a subset of the proper regulars of n. In base 10, the regular numbers are {1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, 80, 100, 125, 128, …}, but the proper regulars are {1, 2, 4, 5, 8, 16, 25, 32, 64, 125, 128, …}, that is, the powers of 2 and 5. In hexadecimal, 1 and all the positive powers of 2 are regular, but the set of proper regulars is finite: {1, 2, 4, 8}. Each proper regular r produces a family of regular numbers that are multiples r × n^ε. In base 10, the proper regular 2 has a family of regulars that include {2, 20, 200, 2000, …}. In this way, the proper regulars can be seen as primitive regulars, simplifying the infinite set of n-regular numbers.

   Regular and Coprime — the number 1 is both regular and coprime to n, since 1 | n and GCD(1, n) = 1.

   Regular Factor — the regular component of a number semicoprime to n. See “Regular Factor”.

Remainder — in division of two integers a/b = d + c where a is not an integer multiple of b, a nonzero residue c left over in the dividend. See MathsIsFun or MathWorld definitions.

Reptend (or “repetend”) — A group of digits (numerals) that repeat in the expansion of a rational number (fraction) in base b. Decimally, 1/7 = .142857142857…, the reptend is the group of digits that repeat: “142857”. The length of the reptend known as the period of 7 in base 10.

Residue — in modular math we write the division problem a/b = d + c as a = c (mod b); the remainder c is called the residue.

   Quadratic Residue — simply, the base n digits in which a square might end. In other words, the residue r of a square k² with respect to base n. Decimally, the squares {0, 1, 4, 9, 16, 25, …} end in {0, 1, 4, 5, 6, 9}; these are the decimal quadratic residues. In base 16, the quadratic residues are several {0, 1, 4, 9}, but base 13 has 7: {0, 1, 3, 4, 9, 10, 12}. The numerals of base n in which a square may not end are called quadratic nonresidues. See the MathWorld definition.

   Reduced Residue System — all the possible residues that are coprime to n, i.e., the set of totatives of n.

Richness* — regarding n-regular numbers k that divide some power of the base (i.e., k | n^e with e ≥ 0), the smallest integer exponent e of base n that k divides. The richness of the number 1 in base n is 0 since 1 | n⁰. Divisors d | n have richness e = 1. Numbers k with richnesses e ≤ 1. Semidivisors k have richnesses that exceed 1. Nonregular numbers have richness as well; in these cases the richness pertains to the regular factor. For coprimes t, the richness is 0 since 1 is the regular factor of t. For semicoprimes, the richness is greater than 1.

Roll Function — otherwise known as “roll right” where it represents mediation or halving, or “roll left” where it represents duplation or doubling. Method of shifting a hexadecimal number rightward or leftward one bit. See the Penjee Programmers 64 Bit Calculator, specifically, the “RoR” or roll-right button, and the “RoL” or roll-left button.

Roll Table — a means of multiplication through powering up or down (geometric progression) on a prime divisor p | n where n is the number base. The method proves particularly handy in bases that are prime powers, specifically octal or hexadecimal. In the case of octal or hexadecimal, the geometric progression is known as mediation (for halving) and duplation (for doubling). See the essay “Making Hexadecimal Useful”.

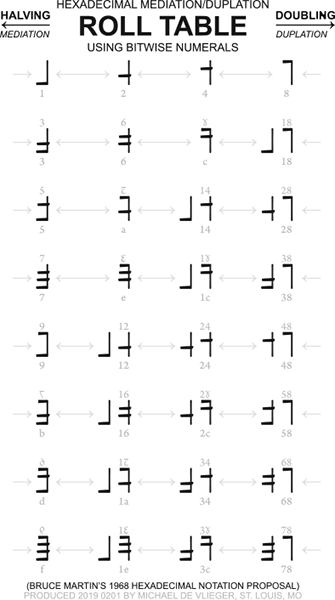
Round Number — A product of many small factors. See MathWorld. For the purposes of this work, we say a number k is round in base n if it is an n-regular number of low richness, or it is a regular quasinumeral or surrogate for a commonly needed fraction. In base 10, the numbers 1000, 1250, 750, or 2,500,000 are round, since “25”, “75” and “125” evoke the fractions 1/4, 3/4, and 1/8 decimally. The number 250,000, colloquially known as “a quarter million”, is round decimally.

   Greater Round* — an n-regular number R_G in the vicinity of a hundred, in this work taken to be 120 ± 30.

   Lesser Round* — an n-regular number R_L in the vicinity of the number of symbols in an alphabet, in this work taken to be 30 ± 6.

R·S·C — The analysis of the nonzero integer n in terms of the infinite sets R, S, and C of positive integers k that are regular (R), semicoprime (S), or coprime (C) to n. The three kinds of numbers are mutually exclusive except that 1 (see “Unit”) is both regular and coprime to n. The infinite sets pertain to the squarefree kernel m of n. For example, the numbers regular to 12, {1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, …}, i.e., the infinite set of 3-smooth numbers listed in A003586, pertain to 6, 18, 24, 36, 48, …, (cf. A033845 = 6 × A003586). The smallest number in the latter sequence is 6. Therefore the 6-regular numbers are regular in any number that shares the strictly-same set of distinct prime divisors of 6, i.e., only {2, 3} and no other prime divisor. For this reason, we may note that R₆ = A003586, using a subscript to denote the infinite set of numbers regular to the squarefree number 6. Since the sets R, S, and C are infinite, we may only capture a finite range bounded by n (i.e., the span 1 ≤ k ≤ n) if we take into account counting functions as in the D·N·T analysis. For R·S·C, we use the regular counting function RCF(n) = A010846(n), the semicoprime counting function ξ_t(n) = A243823(n), and the Euler totient function φ(n) = A000010(n), for R, S, and C respectively. Analogous to A020490, there is a finite set of numbers that have as many regulars 1 ≤ k ≤ n than totatives: {1, 2, 3, 4, 6, 8, 10, 12, 14, 18, 20, 24, 30, 36, 42, 60, 66, 84, 90, 120, 150, 210, 420}, or more regulars 1 ≤ k ≤ n than totatives: {2, 4, 6, 10, 12, 18, 24, 30, 36, 42, 60, 66, 84, 90, 120, 150, 210}. The numbers that have more semitotatives than any other kind {144, 162, 174, 186, 192, 198, 200, 204, 216, …} appears in A294575 (the odd numbers {945, 1155, 1365, 1575, 1785, …} are the focus of A294576). We might also generate lists of the three types of numbers R, S, and C; example: for n = 10, we have divisors {1, 2, 4, 5, 8, 10, (16, 20, 25, 32, …)}, coprimes {1, 3, 7, 9, (11, 13, 17, 19, …)}, and neutrals {6, (12, 14, 15, 18, …)}. The portion of these lists less than n appear in A010846, A243823, and A038566 for R, S, and C, respectively. This work considers R·S·C a generalization of D·N·T, with the divisor of n a special case of n-regular number.

See this page for detail and book references.

The following map plots regulars in orange (g ■), semicoprime numbers in yellow (h ■), coprimes in light gray (t ■), with the number 1 which is both regular and coprime shown in orange at left. Bases n appear vertically in rows, numbers k appear horizontally.

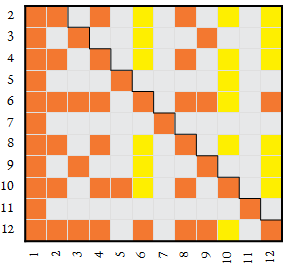
S

Semicoprime — a necessarily composite nonregular n-neutral number s such that gcd(s, n) > 1. A semicoprime is a positive, composite integer not coprime to the base that does not divide any perfect power of the base. Example: decimal 14 is semicoprime since it isn’t coprime to 10 (it is divisible by 2, like 10), and does not divide any perfect power of 10. Another definition of a semicoprime is a positive integer pq < n that is the product of at least one prime divisor p of n, and at least one prime q that is a nondivisor of n. The semitotative is a semicoprime number s < n. (Color canon: h, #fff000; opaque, hh, #f0e4c0)

Also a constitutive arithmetic relationship between two integers a and b such that a does not divide b or any perfect power b^e, and a is not coprime to b.

Semidivisor (g ■) — a necessarily composite nondivisor n-regular, n-neutral number ξ_d | n^e with richness e > 1. A semidivisor divides some perfect power of the base, but not the base itself. Example: decimal 8 divides 1000, but not 10, thus it is a semidivisor. All regular numbers larger than the base are semidivisors. The semidivisor counting function ξ_d(n) is the number of semidivisors ξ_d < n. (Color canon: g, #f47830; compound, gc, #f8a878; impractical, gi, #f8c8a8)

Semidivisor counting function — ξ_d(n) — see “Counting function, semidivisor”.

Semitotative (h ■) — a necessarily composite nonregular n-neutral number ξ_t < n such that gcd(ξ_t, n) > 1. A semitotative is a positive, composite integer not coprime to the base that does not divide any perfect power of the base. Example: decimal 6 is a semitotative since it is less than 10, not coprime to 10 (it is divisible by 2, like 10), and does not divide any perfect power of 10. Another definition of a semitotative is a positive integer pq < n that is the product of at least one prime divisor p of n, and at least one prime q that is a nondivisor of n. The semitotative is a semicoprime number s < n. (Color canon: h, #fff000; opaque, hh, #f0e4c0)

Senary — the number system based on 6, sometimes called “hexal”.

Sender — in communication, the origin or source of the content of a message, transmitted through a medium to be sensed by the receiver and interpreted.

Septenary — the number system based on 7, sometimes called “septimal”.

Sevenfoldness — the state of divisibility by 7.

Seven-smooth —a number divisible by primes that are less than or equal to 7, {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, …}. See OEIS A002473.

Sexagesimal — base 60 number system, rarely “sexagenary”. An adjective pertaining to the number 60. The decimal-coded sexagesimal number system was used by the Sumerians in the third millennium BC, continued by the Babylonians. The system today is used as a decimal auxiliary base to code time and angle.

   Decimal Coded Sexagesimal (DCS) — a base 60 number system that represents each sexagesimal digit decimally. This system is commonly used in our current expression of minutes and seconds. For instance, we express 10000 seconds as 2:46:40 or 2 hours 46 minutes 40 seconds. Each sexagesimal place contains two-digit decimal numbers when they are not in the leading position. The more significant decimal digit is a decade-figure, while the lesser significant decimal digit is the unit-figure, with decimal coded sexagesimal seen as an alternating base. The ancient Mesopotamian representation of sexagesimal used different cuneiform markings as decade- and unit-figures.

Sieve — the process of eliminating numbers from a list given a set of rules. We can sieve for odd numbers by crossing out any even number we see; the numbers left not crossed out are odd. The term is usually applied to testing for primes: this is called a “prime sieve”. See the MathWorld definition.

Significance — in this work, a coefficient or digit k is considered significant if it contributes to the definition of a number other than merely establishing its magnitude. In other words, the digit k helps establish the mantissa of log_n x. The significant digits occur in the significand. In the decimal number 7.5625, all the digits are significant. In 105,000, the digits “105” are significant; the trailing zeros merely establish the exponent of log₁₀(105,000). In the decimal expansion of 1/12, .08333… the digits after the zero are significant, and we merely approximate the ratio when we truncate the infinite series.

In scientific notation, a digit is considered significant if it preserves the certainty of operations involving measurements that have a degree of uncertainty. In this work, we focus on the former notion.

   Significant Digit — See “Significant Digit”.

   Significant Figure — See “Significant Figure”.

Significand — regarding numbers expressed in base n, any numeral that appears between the most and least significant digits, ignoring trailing zeros. For example, in the decimal number 102400, the number 1024 is the significand; if we add 1 to 102400 to get 102401, all six digits comprise the significand. Likewise, in the decimal .390625, all six digits comprise the significand. Proper regular numbers can be derived from any n-regular number by taking the significand. In decimal, the number 250 is regular, but 25, its significand, is its root proper regular. See the MathWorld definition: the meaning in this work is tailored to the topic of number bases, therefore leading zeros are not considered part of a significand.

Span* — used informally in this work, the term pertains to the integers 0 ≤ k < base n. All the numerals 0 through 9 occur in the span of base 10.

Square — a number x multiplied by itself, written x². The number 4 is the square of 2, since it is 2 × 2.

Squarefree — a number n that is not the product of any square s > 1, where s = k², all integers. The number 6 is squarefree since it is 2 × 3 and neither factor is square, but 12 is not squarefree since 12 = 2² × 3. See OEIS A005117 or the MathWorld definition. Varius numbers (■) are composite squarefree numbers in OEIS A120944, hence A120944 ⊂ A5117.

   Squarefree Kernel — The product of the distinct prime divisors of n. For example, the squarefree kernel of 60 = 2² × 3 × 5 is 30 = 2 × 3 × 5. See OEIS A007947.

Sub-base — a base m < n, m usually a divisor of n, integers, such that we can break numerals into several figures or components. In our everyday use of base-60 in the representation of hours, minutes, and seconds, we write each base-60 numeral in decimal. Therefore the sexagesimal conversion of the decimal number 1000, a two-digit sexagesimal number, we write as 16:40. Each sexagesimal numeral is broken into two components which correspond to expression in the decimal sub-base. (In everyday life, we do not write leading zeros, e.g. 9:40 am as 09:40, so it is perhaps more proper to say the notation is decimal-coded.

Subtraction — written a − b = c, the operation of finding the difference c between a and b. We can thus say c + b = a or b + c = a, as subtraction is the inverse operation of addition. The number a is called the minuend, b the subtrahend, and c the difference. See MathsIsFun or MathWorld definition.

Subtrahend — a number m which we subtract from k; in the expression k − m = n, m is the subtrahend. See MathsIsFun or MathWorld definition.

Sum — the result of adding; a total. See the MathsIsFun or MathWorld definition.

   Partial Sum — one of the results in the running total of a series of addends at a given index. In the series 1 + 2 + 3 + 4, the partial sums are 1, 3, 6, and 10; this is because 1 = 1, 1 + 2 = 3, 1 + 2 + 3 = 6, and 1 + 2 + 3 + 4 = 10. See the Mathworld definition.

Surrogation* — a general term applied in this work to a single numeral or a group of numerals that connote a base b number other than the value of the numeral or group. An example of such is the decimal numeral 5, which connotes “half” or “halfway”. A group of decimal numerals, “25” conveys “one quarter (of a hundred)”; in this case, since a group of numerals do not constitute a numeral, we call the group a quasi-numeral.

Symbology — a term sometimes used to describe the general consideration of the design of numerals to use for nondecimal bases. There are two principal approaches, described by Ralph Beard in his 1945 essay, “The Opposed Principals”. The “least change” approach retains our present numerals, only adding transdecimal numerals for bases greater than 10. The “separate identity” approach remakes all the numerals, including those for numbers less than 10. The 2010 essay “A Numeral Toolbox” describes some design techniques one might use to produce their own symbology. See Menninger and Ifrah for more on symbols used in historic number systems.

System, Number — See “Number System”.

T

Tally — a physical reckoning of items counted, usually by writing a stroke for each item counted. Standard tally involves crossing through four previous marks diagonally to mark a fifth mark; in this way the grouping is quinary, and the bundles of 5 are then counted to arrive at a faster answer. See MathsIsFun definition.

Tantus* (■) — a number that is neither a prime power nor squarefree, such as 12, 20, 60, 120, 216, and any highly composite number greater than 6. These numbers are listed in OEIS A126706. The color code for tantus numbers is blue. The name derives from Latin tantus, “so (many)”, since we have a diverse set of distinct primes p | n, and at least one prime p appears more than once, that is, the multiplicity of p in n is greater than 1. The smallest tantus number is 12; other examples are 36, 50, and 686. The highly composite numbers excepting {1, 2, 4, 6} are tantus, as well as the superior highly composite numbers. Therefore, A4490 \ {2, 6} ⊂ A2182 \ {1, 2, 4, 6} ⊂ A126706. Furthermore, plenus numbers, products of multiple composite prime powers, are a special case of tantus number; 36 = 2² × 3² is a plenus number.

Ternary — having to do with 3, also the number system based on 3.

Tetradecimal — the number system based on 14, sometimes called “quattuordenary” or “quattuordecimal”.

Tetravigesimal — a number system based on 24.

Thousand-like* — in base n, the expansion of the cube of n, i.e., n³, written “1000”. The term is used to avoid concocting nomenclature for this number. The decimal number 216 is thousand-like in base 6, since in base 6, 216 = 6³ is written “1000”. The duodecimal great gross (1728 or a dozen grosses) is thousand-like in that base.

Theory, Number — See “Number Theory”.

Threefoldness* — the state of divisibility by 3.

Three-smooth — a number divisible only by primes 2 or 3 or both, {1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, …}. Also multiples k such that 6k are the numbers for which 6 is the squarefree kernel. See OEIS A003586.

Total — see “Sum”.

Totative — a number 1 < t < n that is coprime to n, i.e., GCD(t, n) = 1. Totatives are smaller than the base and have no prime factors in common with the base. The totatives of 10 are {1, 3, 7, 9}. The number of totatives of n is given by the Euler totient function φ(n). One might use the totatives of n as a prime sieve, since primes q that are not factors of base n have a base-n totative t as the last digit when expressed in that base. See MathWorld definition. For various flavors of totative, see this definition of coprime.

Totient — originally an adjective coined by James J. Sylvester in the 19th century, the term describes the set of items counted by the Euler totient function. These items are the numbers less than n that are coprime to n (i.e., 1 ≤ k ≤ n such that GCD(k,n) = 1).

Transdecimal (adjective) — usually said of a numeral, of or pertaining to a base b > 10.

Trecentosexagesimal — a number system based on 360.

Tridecimal — the number system based on 13, also called “tridenary”.

Trigesimal — a number system based on 30.

Trine (adjective) — a number divisible by 3.

U

Unary — a number system based on 1. Such systems have a 1 to 1 correspondence; one item counted is represented by one mark or token. Tally without bundling or grouping can be considered a unary system.

Undecimal — the number system based on 11, also called “undenary”.

Union — the combination of the members of two sets. See the MathsIsFun or MathWorld definition.

Unit (■) — the integer 1, the empty product both a divisor of and coprime to every integer. Since 1 divides every integer, it is also regular to every integer. Some sources define “unit” to mean “totative”, the latter being the term used in this work; here the word “unit” strictly refers to the number 1.

Unique Prime Factorization Theorem — See “Fundamental Theorem of Arithmetic”

Undertrine (adjective) — a number one less than a multiple of 3, i.e., 3x − 1, or a number congruent to 2 (mod 3).

V

Varius* (■) — a composite squarefree number n, such as 6, 10, 210, any primorial greater than 2. These numbers are listed in OEIS A120944. The color code for varius numbers is green. The name is a coinage of 2022, from Latin varius meaning variegated, since n is a product of variegated primes without copies of any of the same primes. In terms of OEIS, A120944 = A5117 \ A40, that is, the squarefree numbers without the primes.

Vigesimal — base 20 number system, rarely “vigenary”. A form of vigesimal was used by the precolumbian Mayan empire. See Mathworld definition.

   Quinary Coded Vigesimal (QCV) — the expression of a base 20 system that encodes digits in groups of 5. The Mayan implementation of vigesimal used numerals that tallied to the base of 5.

0  1  2  3  4

5  6  7  8  9

a  b  c  d  e

f  g  h  i  j

W · X · Y

Wieferich Prime — a prime p such that p² | n^{(p − 1)} − 1 for n = 2; the two smallest terms are 1093, 3511. As regards number bases, the Wieferich primes are such that their unit fractions (1/1093, 1/3511) have binary periods that are maintained from p to p². This work generalizes the definition to any number n. In decimal, 3 is a generalized Wieferich prime, since 1/3 = .333… and 1/9 = .111…; that is, 3 and 3² have the same period of 1. (This fact is a crucial detail regarding the relative utility of the decimal base). In octodecimal (base 18), the number 7 is a rank-3 generalized Wieferich prime, since 1/7 = .2a52a5…, 1/7² = .06b06b…, and 1/7³ = .00h00h…; i.e., they share the period 3.

Z

Zero — a numeral that signifies a null or empty place value. Numerals that are not zero are called “nonzero” numerals; likewise, a number that isn’t zero is described as “nonzero”. When zero appears alone, it is interpreted as signifying “nothing”, but following nonzero numerals, zero merely maintains positional notation. A zero that stands alone to signify nil is neither positive nor negative, but to be precise, when we mean the numbers {1, 2, 3, 4, …}, we use the locution “nonzero positive”. We understand that any position has the value zero when it isn’t specifically occupied by a nonzero numeral, thus we know that the ten-thousands place in the number 2048 has a null value. At the end of a number x expressed in base n, zero signifies that x is divisible by n. The number k of trailing zeros in an integer x signifies that x |n^k. Example, the decimal number 300 is divisible by 100.

   Leading Zero — a zero written to precede the significand in standard positional notation, in a place where a nonzero digit would represent the largest part of a number written in base n. In integers, leading zeros are normally unwritten, the places that are greater than the integer understood to be null. Example, decimal “007” has two leading zeros that are insignificant but maintain three digits for whatever reason. In the fractional number “0.0625”, the zero before the decimal point appears merely for clarity, but the zero immediately after the decimal point maintains the place values of the digits that follow it. Thus, “.0625” represents 1/16 in base ten, but “.625” is 5/8 without the leading zero.

   Significant Zero — a zero value that appears between nonzero digits, within the significand. (This is a slightly different definition, tailored for the discussion of number bases, than appears at Rensselaer Polytechnic, for example, that pertains to technical measure and scientific notation.) For instance, in the decimal number “102854”, the “0” in the ten-thousands place is significant, since it maintains that place between the nonzero place values. Leading and trailing zeros are not significant (in this work's definition). For instance, if we write the decimal number 12 for whatever reason “0012”, the two leading zeros are insignificant. Similarly, in the decimal number 12500, the last two zero digits are not significant, but serve to maintain the magnitude of the number. In the decimal expansion of 1/8, we may write “0.12500000”, the leading zero perhaps for clarity, but only “.125” is significant.

   Trailing Zero — a zero that follows the significand in standard positional notation, in a place where a nonzero digit would represent the smallest part of a number written in base n. In integers, the trailing zeros merely support the magnitude of the number represented, cf. the difference between decimal 250 and 2500. If we did not write the trailing zeros of an integer, we would be left confused. In a fractional number such as decimal “.375000”, the trailing zeros are unnecessary.

This page last modified Wednesday 23 June 2022.
Copyright © 2022 Michael De Vlieger