 |
Neutral (Number)Glossary |
Neutral Number
Consider the nonzero integers ξ and base n. We say ξ is neutral to n if it neither divides n nor is coprime to n. Neutral numbers ξ are indicated by 1 < GCD(ξ, n) < ξ. In other words, ξ is neither a factor nor a totative or coprime number with respect to n. Neutral numbers 1 < ξ < n are nondivisors in the cototient of n.
The map below plots neutral numbers in yellow-orange; while coprimes (totatives) appear in gray, divisors in red, and the number 1, both coprime and regular, in purple. Number base n appears on the vertical axis and digit k appears on the horizontal.
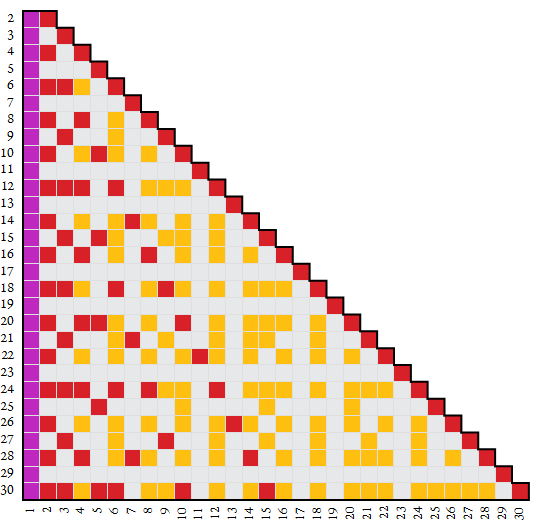
Neutral counting function.
Neutral numbers in the span of n that are counted neither by the divisor counting function τ(n) nor the Euler totient function φ(n). Therefore we can write a neutral counting function ξ(n) = OEIS A045763 thus:
ξ(n) = n − (τ(n) + φ(n) − 1)
or in terms of the OEIS:
A045763(n) = n − (A000005(n) + A000010(n) − 1),
For prime p, ξ(p) = 0. In other words, prime bases p do not have neutral numbers smaller than p. This said, we can construct neutral numbers larger than prime p. Any perfect power pm with m > 1 is neutral to p, the smallest of which is of course p², further, any product pq with q ≠ p is neutral to p, the smallest of which is of course 2p when p ≠ 2, otherwise 3p.
Neutral numbers must be composite
The neutral number is implicitly composite since a prime must either divide n or be coprime to it [1, 2]. Further, regarding neutral numbers k < n, base n must also be composite.
2 kinds of neutral number.
There are two species of neutral number [2]. These species have markedly different behaviors with respect to base n. A semidivisor ξd is an n-regular number k that divides some perfect power of n greater than base n itself. A semicoprime ξt is a number k that does not divide any integer power of n and is not coprime to n. (A semitotative is a number semicoprime to n and less than n, i.e., 1 < ξt < n) The number of neutral numbers ξ < n is given by the neutral counting function ξ(n) = n − (τ(n) + φ(n) − 1), where τ(n) is the number of divisors of n, and φ(n) is the number of totatives of n.
The map below only plots neutral numbers in the two species. Orange indicates semidivisors, while yellow indicates semitotatives. Number base n appears on the vertical axis and digit k appears on the horizontal.
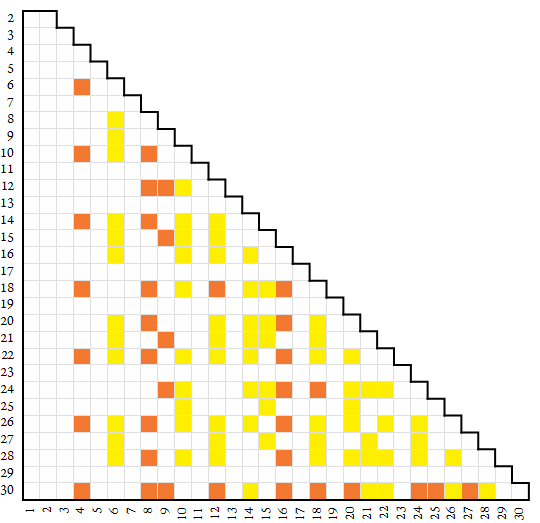
Testing for constitutive neutrality.
We know that an n-neutral number ξ is composite and neither divides nor is coprime to n. Therefore, f an arbitrary nonzero positive integer k is composite and if 1 < GCD(n, k) < k, k is neutral to n. For k > n, the smallest n-neutral number is always the smallest number exceeding n that is not coprime to n, since all divisors d ≤ n.
Neutral numbers in the OEIS.
There are a few sequences in the OEIS that examine neutral numbers 1 < ξ < n (i.e., nondivisors in the cototient of n) and their species, the semidivisors 1 < ξd < n and semitotatives 1 < ξt < n. Asterisked sequences were contributed by this work’s author.
A045763: Neutral counting function ξ(n) — here neutrals are termed “numbers unrelated to n”.
A061228: Smallest n-neutral k > n.
A073759: Largest n-neutral k < n.
A133995: Nondivisors in the cototient of n.
A304571: Characteristic function of nondivisors in the cototient of n.*
A300859: A045763 recordsetters (highly neutral numbers)*
A300914: Records in A045763.*
A295523: Nonprimes that have more semidivisors than semitotatives (the two kinds of n-neutral number).*
A294492: Recordsetters for A045763(n)/n.*
A300858: A243823(n) − A243822(n). (A300858(p) for p prime = 0, for n = {6, 10, 12, 18, 30}, A300858(n) is negative.)
A300860: A300858 recordsetters.*
A300861: Records in A300858.*
Semidivisors 1 < ξd < n:
A272618: Row n of this sequence lists semidivisors ξd < n.
A293555: Numbers n that set records for the semidivisor counting function ξd(n).
A299991: Numbers n that have more semidivisors than divisors (two kinds of n-regular number).
A299992: Numbers n that have fewer semidivisors than divisors.
A300155: Numbers n that have equal numbers of semidivisors and divisors.
A300156: Numbers n that set records for the difference between the semidivisor counting function ξd(n) and the divisor counting function τ(n).
A289280: Smallest n-regular r > n (the smallest semidivisor r greater than n).
Semitotatives 1 < ξt < n:
A243823: Semitotative counting function.*
A272619: Semitotatives of n.*
A304572: Characteristic function of numbers m such that m divides no integer power of n yet gcd(m, n) > 1.*
A292867: A243823 recordsetters.*
A293868: Records in A243823.*
A096014: Smallest m semicoprime to n: product of least prime factor p and smallest prime q that does not divide n.
A291989: Least m > n semicoprime to n.*
A294575: Semitotative-dominant numbers.*
A294576: Odd Semitotative-dominant numbers.*
A295221: Semitotative parity numbers.*
Color code.
In this work, neutral digits are represented by (■ web #ffc010, print 25m 100y), but more often, the two species are coded. The semidivisor (■ web #f47830, print 66m 100y) and semicoprime (■ web #fff000, print 100y). In detailed maps, there are many flavors of these species; see their entries for more information.

Provenance of the term “neutral”.
The term “neutral” in the constitutive sense is a 2008 coinage of the author of this site, while the usage of the Greek letter ξ to denote n-neutral numbers was used in the early 20th century and pertained to the neutral counting function, but the reference is lost. At OEIS, the terminology is often “numbers ξ unrelated to n”. The author and certain others find this usage unsatisfactory, the former on account of one species of neutral numbers (i.e., the semidivisor) being a product of numbers d that also divide n. It would thus appear that “unrelation” might instead pertain to numbers k coprime to n, as these do not have prime divisors in common.
The term was somewhat reluctantly borrowed from the Latin, at the risk of confusion with very many other mathematics and general concepts dubbed “neutral”, since an n-neutral number neither divides nor is coprime to n. The usage of Greek κανενας (kanenas) and terms from other languages were thought to render what seems to be a more prominent arithmetic concept overly “alien”, so these were abandoned.
The coinage of a term for the noncoprime nondivisor itself was reluctant but for the fact that it simplifies the locutions (“nondivisors in the cototient“, “noncoprime nondivisor”, “numbers that neither divide nor are coprime”) that would otherwise be applied to n-neutral numbers.
The terms “semidivisor”, “semitotative”/“semicoprime”, and “noncoprime nondivisor” are likewise coinages of the author.
References.
[1] Ore 1948, Chapter 4, “Prime Numbers”, page 50, specifically: “Lemma 4-1. A prime p is either relatively prime to a number or divides it” and ensuing proof.
[2] De Vlieger 2011, “Neutral Numbers”.