 |
Range foldingGlossary |
Range folding
Concerning regular divisibility tests, the practice of employing a simple prime divisor test on a specific digit from the least significant in order to render more practical an impractical divisibility test.
Qualities of a regular divisibility test
Let the nonzero positive n-regular integer r | nε with richness ε ≥ 0. We can test an arbitrary nonzero integer x to see if it is an integer multiple of r in base n by the examination of a block of the least significant, rightmost digits. The number of digits in the block is the richness ε. If the block of digits matches one of nε/r combinations, each with ε digits, then r | x (x is divisible by r). Let the reference range be the list of combinations to which one needs to refer when using a regular divisibility test. For the purposes of this essay we regard the number of combinations in the reference range as its breadth nε/r.
For divisors, the case is rather simple provided the base is not too large; we have single digits as the combinations. The evenness or parity test might perhaps prove the most common in any base since 2 is the smallest prime. In decimal we know a number x is divisible by 2 (i.e., 2 | x) if it ends in one of 10/2 = 5 single-digit combinations {0, 2, 4, 6, 8}. In tetradecimal (base 14) we would have 14/2 or 7 single digit combinations {0, 2, 4, 6, 8, a, c} (where “a” is digit-10 and “c” is digit-12). In duodecimal (base 12) we also have the test 3 | x using 12/3 = 4 single digit combinations {0, 3, 6, 9}.
The regular tests also include semidivisors (nondivisor regular numbers). In decimal we can test 4 | x using 10²/4 = 25 two-digit combinations {00, 04, 08, 12, 16, …, 92, 96}, and we can test 25 | x using 10²/25 = 4 two-digit combinations {00, 25, 50, 75}. We see that perhaps 25 two-digit combinations might be a little much to memorize. We have a decimal test for 8 | x using 10³/8 = 125 three-digit combinations {000, 008, 016, 024, …, 984, 992}. At this point it is clear that the test is impractical for most people.
Folding the reference range
Under certain conditions we can “fold” or shorten the reference range by applying a simple divisibility test pertaining to a small prime divisor P on a non-final digit. We call this prime divisor P the folding factor for the sake of this essay. We note that P must be a factor common to n and r. We also note that range folding is usually useful for regular numbers r with p < √n. For n = 10, we observe that the regular tests pertaining to powers 2m are less practical than those for 5m, since the breadth of their reference ranges are 5m and 2m, respectively.
Let us number the digits, proceeding leftward from the radix point or rightmost end of the base n number x by the place value they represent. For instance, in the decimal number “12345”, the “5” appears at D = 0, since the place value occupied by “5” is 100 = 1. Thus, a “3” appears at D = 2 since it has place value 10² = 100. Range folding applies the prime divisor test to a digit at D between 1 and 3 inclusive. This then decreases the number of combinations quite effectively.
Looking at decimal 8 | x, we note that 8 | 10³ thus has richness ε = 3, thus the breadth 1000 / 8 = 125. There are 125 combinations that are the multiples 8k for 0 ≤ k ≤ 125. We might regard about 30 two- or three-digit combinations as practical (taking 30 as about the length of an alphabet). If we check the evenness of the D = 2 place (the hundreds place), we can fold the reference range to breadth 25. The folded regular test is thus:
“An arbitrary nonzero integer x is divisible by 8 in base ten if the hundreds place is even and the 2 least significant digits are one of {00, 08, 16, 24, 32, …} (13 possible values) or the hundreds place is odd and the 2 least significant digits are one of {04, 12, 20, 28, 38, …} (12 possible values).”
Range folding likely happens mentally concerning the decimal divisibility test for 4. Rather than that breadth of 25 two-digit combinations, we perhaps see it as the following:
“An arbitrary decimal nonzero integer x is divisible by 4 if the tens place is even and the least significant digit is one of {0, 4, 8} or the tens place is odd and the least significant digit is one of {2, 6} (5 possible values).”
Range folding in decimal largely applies to 4 | x and 8 | x. We observe that the tests for the perfect powers of 5 (i.e., 25, 125, 625) are less-necessary but more practical than the tests for the related perfect powers of 2. For example, 25 | x has breadth 4, 125 | x has breadth 8, and 625 | xhas breadth 16.
Extension to nondecimal bases
In nondecimal bases, range folding operates much like it does in decimal, but might engage a different folding factor P.
In even squarefree semiprimes such as 6, 14, 22, etc., these rules might look familiar and could pertain as they do in decimal to 4 | x and 8 | x. The senary (base 6) only has breadth 9 and is solidly practical, with 8 | x at breadth 27 likewise acceptable, but we might shorten 16 | x to 27 three-digit combinations with an evenness test at the thousandlike D = 3. In base 14, we could shorten 4 | x from 49 to 7 combinations:
“An arbitrary tetradecimal nonzero integer x is divisible by 4 if the fourteens place is even and the least significant digit is one of {0, 4, 8, c}, or the fourteens place is odd and the last digit is one of {2, 6, a}.”
In this case the rule is reminiscent of the decimal equivalent.
For other bases, perhaps practically those that have the factor 3, we might consider rules that pertain to that folding factor rather than P = 2.
A duodecimal example 9 | x illustrates the effect in a nondecimal base. The duodecimal semidivisor 9 has richness ε = 2, thus the breadth nε/r = 144 / 9 = 16. There are 16 (or one dozen four) possible multiples of 9 that are less than duodecimal “1000” (decimal 1728) in the reference range, which is perhaps practical as it is less than about 30. If we check the D = 1 place (the dozens place) for divisibility by 3, we can fold the reference range to 4. This doesn’t render an impractical regular test practical, instead it makes for an even more convenient folded regular IDT. The folded IDT is thus:
“An arbitrary nonzero integer x is divisible by 9 in base r = 12 if the dozens place is an integer multiple of 3 and the least significant digit is one of {0, 9}, or the dozens place is one more than an integer multiple of 3 and the least significant digit is one of {6}, or the dozens place is one less than an integer multiple of 3 and the least significant digit is one of {3}.”
In a base 12 world, the concept of threefoldness might prove much more relevant so as to merit its own nomenclature (see link for more). Therefore we use the word “trine” meaning divisible by 3 much like “even” means divisible by 2, and “nontrine” meaning indivisible by 3 much like “odd” means not divisible by 2. There are two kinds of nontrine; “overtrine” pertains to 3k + 1, examples, {1, 4, 7, 10, 13, …}, and “undertrine” − 1 pertains to 3k + 1, e.g., {2, 5, 8, 11, 14, …}. Using this language the above rule is perhaps streamlined:
“An arbitrary nonzero integer x is divisible by 9 in base r = 12 if the dozens place is trine and the least significant digit is one of {0, 9}, or the dozens place is overtrine and the least significant digit is 6, or the dozens place is undertrine and the least significant digit is 3.”
There appears to be a sensible limit on the size of the folding factor P. The case of parity (pertaining to 2) is simple and literally binary. The case for threefoldness (pertaining to 3) is a bit more complicated with 3 cases. For P = 5, we would have 5 cases, maybe a bit more than average memory might recall for what should be a handy test. Fortunately these cases require P to be the least prime divisor of n (or perhaps merely P < √n), where n ≥ 35. Let’s examine a perhaps-ridiculous example of r = 25 in base n = 55 = 5 × 11. We note that 25 | 55². Unfolded, the regular rule is as follows:
“An arbitrary pentaquinquagesimal nonzero integer x is divisible by 25 if the 2 least significant digits are one of {“0,0”, “0,25”, “0,50”, “1,20”, “1,45”, …, “54,30”} (121 possible values).”
This is made relatively “less insane” through the following (if one might muster the five cases):
“An arbitrary pentaquinquagesimal nonzero integer x is divisible by 25 …
if the hundredlike place is an integer multiple of 5 (i.e., 5k) and the last digit is one of {00, 25, 50}*,
or the hundredlike place is 5k + 1 and the last digit is one of {20, 45},
or the hundredlike place is 5k + 2 and the last digit is one of {15, 40},
or the hundredlike place is 5k + 3 and the last digit is one of {10, 35},
or the hundredlike place is 5k + 4 and the last digit is one of {5, 30}.”
* We note that these decimally expressed digit pairs are single digits in base 55.
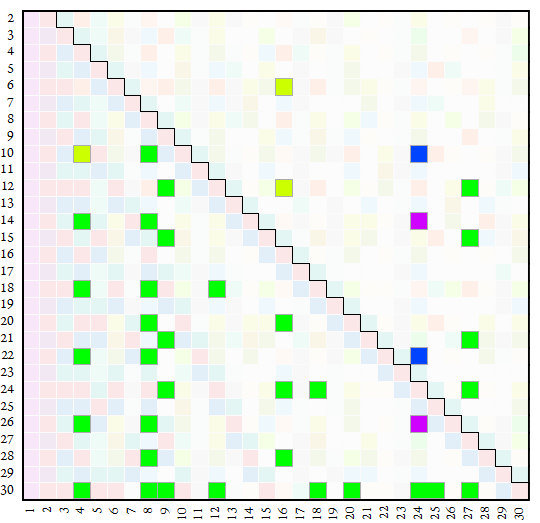
The map below shows some candidates for range folding. Recall that range folding requires the number r to be a semidivisor that is not a perfect prime power, thus necessarily composite, in a number base n that is also neither prime nor a perfect prime power. Number base n appears on the vertical axis and digit k appears on the horizontal. Numbers that benefit from range folding are highlighted, with brilliant green showing numbers that more or less require range folding, lighter yellow green numbers that do not require range folding however it could prove helpful, blue being numbers that inherit the range-folded test, combining it with the omega test, and purple inheritors combining the regular test with the alpha.
Impractical evenness tests
We are inclined to consider the evenness (or parity) test essential and ever-practical, especially in an even base. The concept of even and odd seems downright basic.
At some point an even base n = 2k has breadth k that exceeds an ability to acquire for the average person. Today we teach kids about even numbers in kindergarten and first grade; in decimal, k = 5 and is simple to acquire. At what point do we render the evenness test impractical? As a rule of thumb we might consider k = 30 as the limit, perhaps teaching evenness at a slightly older age. Even then, this might be too broad for young children to grasp. Unfortunately, range folding is reliant on a small prime folding factor P; we cannot range-fold the evenness test.
The counterintuitive thought is that the evenness test (tantamount to the omega or digit-sum divisibility test) is perhaps more practical for large odd bases n than large even bases!
Range folding as an effect of cognitive arithmetic
The n-regular numbers r that have reference ranges that can be folded are few, limited by human cognition. Similarly, the folding factors that are practical may be limited to only 2 and 3 (perhaps 4 and 5), and the breadth for most people will be some number around 30. We must bear in mind that a divisibility test is simply a “handy trick” to gauge, say, the amenability of a denominator to simplification. At some point people will turn to arithmetic (division) instead of using a divisibility test. Thus, the parameters for range folding are rather narrow.
In short, range folding seems to be a method that only might convert a couple n-regular numbers r on the margin to practicality, provided base n is not a perfect prime power, the folding factor P is 2 or 3, and the richness ε > 1 is low.