 |
The Constitutive FunctionsRadicologist Essays |
RSC Pertains to the Squarefree Kernel of n.
Let the infinite set C include all numbers coprime to base n, meaning gcd(c, n) = 1 for all c in C. It follows that 1 and all primes q that do not divide n are in C, and all products of any primes q to any positive integer multiplicity also are in C. Therefore it is plain to see that the set C is unbounded and infinite. Example: the set C pertaining to 10 is {1, 3, 7, 9, 11, 13, 17, 19, 21, 23, 27, 29, …}. It is easy to see a pattern. C contains all numbers c such that c (mod n) ≡ t in T, where T is the (necessarily finite) set of totatives T of n (i.e., the reduced residue system of n). C is clearly infinite by induction.
Let the infinite set R include all “regular” numbers r such that r | ne with integer e ≥ 0. It is easy to see that the divisor d | n is a special case of r where 0 ≤ e ≤ 1. Therefore R contains 1 and the other divisors d, as well as any number r that divides some power of n. Since we can always increment e to obtain a larger perfect power ne, and since those powers have some divisors r (at least ne itself) that do not divide n(e − 1), by induction we show R to be infinite. Example: the set R that pertains to 10 is {1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, …}; this contains 1 and the other divisors of 10 (i.e., 2, 5, 10) and integers k | 10m, with m > 1, i.e., (4, 8, 16, 20, 25, 32, 40, 50, 64, …). The set R is easy to describe: it is the union of the perfect powers pm of the prime divisors p | n and their products. Since the combinations of primes p | n with multiplicity are infinite and any product of such a combination is n-regular, R is clearly infinite.
The intersection of R and C is {1}, since 1 | n and gcd(1 , n) = 1; this is a unique property of the number 1. Outside of this term, sequences R and C are distinct but not coterminous; we can produce numbers outside of these infinite sequences. Just taking the positive integers that do not exceed 10 into account, regarding 10, we have the numbers in C {1, 3, 7, 9} and those in R {1, 2, 4, 5, 8, 10}. We have not listed 6, which lies outside of both sets: 6 is a nondivisor in the cototient of 10 and does not divide any perfect power of 10. The numbers that do not appear, regarding 10, include {6, 12, 14, 15, 18, 22, 24, 26, 28, 30, 34, …} = OEIS A105115.
We know that there are numbers ξ such that 1 < gcd(ξ, n) < ξ. These numbers ξ are “neutral” to n since they neither divide nor are coprime to n. For n = p prime, there are no neutral ξ < p, but we can show that ξ | pe for e > 1 are neutral, since they cannot divide p, but also ξ (mod p) ≡ 0 and are not coprime to p. Further we can produce composite ξ from the smallest prime divisor p of p (i.e., p itself) and the smallest q coprime to p (the least prime that does not divide p; for any odd prime p, q = 2). This ξt = pq does not divide p since it is larger than p and for the factor q not one of p, and it cannot be coprime to p since gcd(pq, p) = p. Therefore we have produced two species of neutral ξ that apply to all numbers n, even for n = prime p that exceed p, but we have shown that there are neutral ξ < n for composite n > 4. We know that one species, those that divide a perfect power ne for e > 1, ascribe to regular R. The second species of neutral numbers does not ascribe either to R or to C, for the condition 1 < gcd(ξ, n) < ξ. We know that we can produce an infinite number of composite numbers that are the product of at least one prime p | n and q such that gcd(q, n) = 1. Therefore we can produce a third infinite set S distinct from the union of R and C. We know from the proofs related to neutral numbers that there are no other species and thus we can divide all positive integers into members of the three infinite sets R, S, and C that are coterminous except for the case that applies to 1. This third set S contains numbers ξt semicoprime to n.
In base n, the three sets primarily manifest themselves in the behavior of the expansion of fractions. The n-regular numbers r in R as denominators have terminating expansions in base n. The numbers c > 1 coprime to n that appear in C, when a denominator, have purely recurrent expansions in base n. Finally, the numbers ξt in S as denominators have a mixed recurrent expansion in base n.
Let us refer to the “RSC” relationships as the “constitutive arithmetic relationships” of n.
Constitutive classes pertain to squarefree kernels.
It is known that the numbers T coprime to n in C are also coprime to any other number divisible by the distinct prime divisors p of n. We can extract the squarefree kernel of n, rad(n) = OEIS A007947(n), simply by multiplying the distinct prime divisors of n. For instance, rad(12) = 6, since 6 = 2 × 3, and 12 = 2² × 3. Therefore, the numbers T coprime to the dozen are also coprime to 6, and indeed to any other number that is the product of both 2 and 3 (i.e., numbers in A033845). Thus we can subscript C6 since the numbers coprime to 6 are also coprime to (6, 12, 18, 24, 36, 48, …).
We know that another definition of regular number r is one such that all prime divisors p also divide n. Therefore it too pertains to A007947(n), and we can likewise subscript R6. Since the sets are coterminous (with the exception of the number 1 shared between R and C), we can subscript S6. Indeed the 12-semicoprime numbers ξ = {10, 14, 15, 20, 21, 22, 26, 28, 30, 33, …} are shared between any base 6 × R6 = 6 × A003582.
Therefore, the RSC configuration for duodecimal is also shared by senary, octodecimal, tetravigesimal, etc., and that for decimal is shared with vigesimal, etc.
This means we can talk of shared efficiencies between bases with the same squarefree root. The regulars, semicoprimes, and coprimes of these bases are the same; the numbers whose fractions terminate, are mixed recurrent, and recurrent are shared, etc.
Reflecting on this essay 3—9 April 2019, I made some further observations about the constitutive relationships.
Relative size of the constitutive classes.
For p prime, only perfect powers pm, integers, are in Rp; the scale of is related to logp(x). Multiples kp that are not perfect powers are s in Sp, and all other numbers and 1 are c in Cp. From the definition of semicoprime, we know that any number s = cpm. We know the totient ratio φ(p)/p approaches the asymptote 1 as p increases. Therefore, for primes, Cp >> Sp >> Rp, with the first ever larger, last ever smaller as p increases. We know that primorials pi# minimize the totient ratio. It seems that Rp# is larger than that for a prime, but still related to log(x). Therefore Sp# would seem to be the largest of the three: Sp > Cp >> Rp, and for no number n > 1, Rp would dominate. Regular numbers among k for composite n seem rather common when k is small, but are ever scarcer as k increases. An open question: are there more coprimes in the universe than semicoprimes?
Primes and composites in the constitutive classes.
Starting with primes, we observe two axioms. A prime p either divides n or is coprime to n when a nondivisor q. The only divisors of prime p are 1 and p itself; all other k < p are coprime to p. Therefore, we know that the only primes in R are the prime divisors p | n, and all other primes q are in C. We know the number k = 1 is at once coprime to n and divides it. Therefore the balance of these two classes is comprised of composites. In the case of C, the composites are multiples of any multiplicity of any number of distinct nondivisor primes q. The multiples of any number of distinct prime divisors p in any multiplicity are regular to n and are in R. We know that given the first axiom in this paragraph, S can only contain composites; this is also supported by the definition of the semicoprime. The composites in this class are any product of at least one prime p and at least one prime q. From this examination, it might seem easy to justify the relative scales of these infinite classes, that clearly, C and S must be very large and R, though infinite, only a trickle compared to the other two classes.
The case n = 1.
Let’s think of n = 1, since it is a unique case among the nonzero positive integers. Recall that 1 is the empty product, the multiplicative identity. Because of this, 1 is coprime to all primes; no prime is regular to 1, in fact, 1 is the only regular number with respect to 1, making R finite. Furthermore, since all primes are coprime to 1 and none are regular, there can be no semicoprimes with respect to 1. The class S is null. Thus the class C is completely infinite with respect to 1, as any product of primes is coprime to 1.
The totient ratio as a means of scaling the classes.
Seeing as the size of R compared to the other classes is vanishingly small, O(x) in comparison, we might regard the totient ratio φ(n)/n as a key metric when examining the constitutive classes with respect to n. This ratio as stated above is maximized by primes p as p approaches infinity, and is minimized by the primorials p#. The totient ratio is that ratio of all nonzero positive integers in Z that are coprime to n, since any k ≡ t (mod n), where t is a totative t < n with gcd(t, n) = 1, is likewise coprime to n. Since R varies approximately as to log(x), and is O(x) in comparison to the two other constitutive classes, we might mostly ignore it. Therefore the scale of S is very near 1 − φ(n)/n. We can plot the totient ratio:

The y axis of this chart is the totient ratio, ranging from 0 at the bottom-most gray line and 1 at the top-most. The x axis equates to the index of the greatest prime factor of rad(n). The blue line joins 2 at left to the odd primes. The red line joins 2 at left to 6 and the primorials. The function φ(p)/p = (p − 1)/p for primes p. It is simple to write the ratios: 1, 1/2, 2/3, 4/5, 6/7, 10/11, 12/13, etc. For primorials, we might refer to the handy OEIS: φ(pi#)/pi# = A038110(i)/A060753(i). The first few ratios φ(pi#)/pi# are: 1, 1/2, 1/3, 4/15, 8/35, 16/77, 192/1001, 3072/17017, ….
The ratios for any other number with the greatest prime divisor px fall between the blue and red lines. The first isolated dots in the third column pertain, top to bottom, to 15 = 3 × 5, and 10 = 2 × 5, therefore from top to bottom in the 3rd column we have 5, 15, 10, 30. No two squarefree numbers have the same totient ratio since they are products of different combinations of primes.
Odd, Even, and other numbers in the chart.
Let’s examine a more detailed chart with the squarefree k labeled. We've traced the sequence of primes as the upper bound of the totient ratio for k with gpf(k) = pn in blue, and the sequence of primorials (OEIS A002110) as the lower bound of same in red.
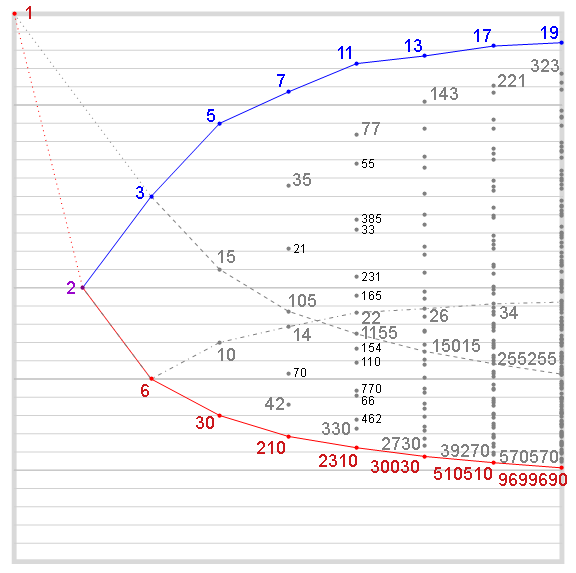
Likewise we can trace the odd numbers k with gpf(k) = pn that have the lowest totient ratio. These are shown joined by a dashed gray line, forming the sequence {3, 15, 105, 1155, 15015, 255255, 4849845, 111546435, …} (OEIS A070826). These are p#/2, i.e., primorials divided by 2. Note the plot of φ(1)/1 = 1 at upper left corner. In our case we include 1 in this sequence (joining it with a dotted gray line), as it is odd. For k = 105 (n = 4), we have totient ratio 16/35 < ½, thus is the odd number with the smallest greatest prime factor that has more semicoprimes than coprimes (i.e., S > C). (It also seems that 105 is the smallest odd number overall with totient ratio less than ½.)
The even numbers k with gpf(k) = pn that have the lowest totient ratio appear joined with a dotted and dashed gray line. The numbers that comprise this sequence are 2 joined with 2p, {2, 6, 10, 14, 22, 26, 34, 38, …} (OEIS A077017). Since these numbers are even, their totient ratios can never exceed ½. Therefore no even number has φ(k)/k > ½. Numbers that are perfect powers of 2 have φ(n)/n = ½. We can say that numbers dominated by coprimes (i.e., C > S) are odd or perfect powers of 2. We include the powers of 2 since the totient ratio is exactly ½, and R must count for some infinitesimal portion of the non-coprime half. This implies that only odd numbers appear above the middle of the chart.
The numbers {6, 15, 35, 77, 143, 221, 323, …} (OEIS A006094, products of 2 successive primes) are the numbers k with the second-highest totient ratio for k with gpf(k) = pn. The numbers {3, 10, 42, 330, 2730, 39270, 570570, 11741730, 281291010, …} (pi#/p(i − 1), OEIS draft A306237) are the numbers k with the second-lowest totient ratio for k with gpf(k) = pn.
Let’s consider the numbers k with gpf(k) = pn with φ(k)/k that meet or barely exceed ½. These numbers (apart from 2) are odd: {1, 2, 3, 15, 21, 231, 273, 255, 285, 167739, 56751695, 7599867, 3829070245, 567641679, 510795753, 39169969059, 704463969, 3717740976339, 42917990271, 547701649495, 45484457928390429, 59701280265935165, …}. Writing the multiplicities of primes pi in the i-th position, starting from the right as in a decimal number we have {0, 1, 10, 110, 1010, 11010, 101010, 1000110, 10000110, 101110010, 1101111100, 10111010010, 111100111100, 1101101010010, 11000111100010, 111010101100010, 1010001011010010, 10111110001100010, 100010101101100010, 1010100010010111100, 11111101001100100010, 110000110101111110100, …}. Aside from the final zeros that correspond to odd terms, there does not seem to be a pattern to the prime divisors of terms in this sequence. The terms jump up and down in scale such that it leaves us with open questions regarding the smallest odd term in the sequence.
Finally, consider the numbers k with gpf(k) = pn with φ(k)/k that meet or lie just below ½. Apart from the first 3 terms, these appear to be all odd: {2, 6, 10, 105, 165, 195, 4641, 5187, 5313, 266133, 8870433, 3068957045, 11063481, 10164297, 667797009, 909411789, 32221169781185, 1963007211216415, 421522466365, 3012887561310445, …}. Again these correspond to {1, 11, 101, 1110, 10110, 100110, 1101010, 10101010, 100011010, 1110001010, 11100110010, 101111011100, 1100001110010, 10001010110010, 110010011010010, 1100100100110010, 11111000011011100, 110111100101101100, 1000011010100111100, 11101010010011101100, …}. Again, apart from the final zeros that correspond to odd terms beyond the first 3, there does not seem to be a pattern to the prime divisors of terms in this sequence. The terms jump up and down in scale, however, we can be absolutely sure that 105 is the smallest, examining the 227 − 1 (i.e., 134,217,727) terms k for n < 27 (Something that remains to be done; we have the 20 smallest terms).
The chart below pans out to include 100,000 columns:

We see that the totient ratio for primes indeed converges toward 1; in fact, the ratio for the 100,000th prime (i.e., 1299709) is 0.999999230597…. The red line that serves as the lower bound for numbers n that have a greatest prime factor that increases as we move right has not converged toward 0 as fast. This is because we are multiplying the previous (leftward-plotted) term by a number that is converging toward 1, so the recurrent reduction of is slowing. It seems that the red line would never get to 0 but we consider a product of all primes; even in this product, 1 is coprime to it, so φ(n) must at least be 1. In this chart, the smallest value of φ(n)/n is 0.0398807… (rounded); it pertains to the 100,000th primorial.
Summary.
There are three constitutive classes with respect to n that are mutually exclusive except in the case of k = 1. These are the coprime, the semicoprime, and the regular classes. A number k is said to be regular to n if k | ne with integer e ≥ 0, integers. An integer k is coprime to n if gcd(k, n) = 1. Finally, we define a third class as consisting of necessarily composite k that are the product of at least one prime p | n and at least one prime q such that gcd(q, n) = 1. We discussed the nature of primes and their appearance only in the coprime and regular classes, and the special nature of the number 1. We demonstrated that the coprime and regular classes pertain to the squarefree kernel of n and since these two classes pertain thus, the semicoprimes also pertain to the squarefree kernel of n. We examined the infinite scales of these classes relative to one another and assessed them using the totient ratio φ(n)/n.
It is for the reasons that the constitutive classes are infinite for n > 1 and pertain to the squarefree kernel of n that we might regard them as paramount rather than the divisor counting function paired with the Euler totient function, and the class of numbers that are neither divisors nor coprime to n I called "neutral" to n. The fact that the divisor is merely a special case of regular number seems to undergird the importance of the constitutive relationships. Since the scale of the regular constitutive class R is insignificant compared to that of the other two classes, the totient ratio φ(n)/n serves as a means by which we can assess the relative scale of these infinite classes with respect to n.
Written 2 August 2018 and extended in April 2019 by Michael Thomas De Vlieger.