OEIS A347113.
A sequence of Grant Olson.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0902-0927.
Abstract.
We examine the lexicographically earliest sequence OEIS A347113 in an attempt to explain a certain feature in the scatterplot wherein a tower of numbers repeatedly sets consecutive records. We find that the “towers” comprise the tail of an increasing run. The towers are Cunningham chains, however, we consider the possibility of certain poorly divisible composite terms k that could also contribute to tower-building. We show an association of towers with instances j | k but k sharing 1 ≤ d < ω(j) prime divisors p with j. We also study signatures present in increasing and decreasing runs. A summary of findings appears along with some open questions about the sequence.
Click here for the outline.
Introduction.
Let a(1) = 1; for n > 1, a(n) is the least novel positive number k such that k ≠ j and gcd(k,j) ≠ 1, where j = a(n−1) + 1. This is OEIS A347113 which begins:
1, 4, 10, 22, 46, 94, 5, 2, 6, 14, 3, 8, 12, 26, 9, 15, 18, 38, 13, 7, 16, 34, 20, 24, 30, 62, 21, 11, 27, 32, 36, 74, 25, 28, 58, 118, 17, 33, 40, 82, 166, 334, 35, 39, 42, 86, 29, 44, 48, 56, 19, 45, 23, 50, 54, 60, 122, 41, 49, 52, 106, 214, 43, 55, 63, 66, 134, 51, 64, 70, ...
a(2) = 4 since gcd( j,k) = gcd(2,4) = 2, but all smaller qualified k are coprime to j.
a(3) = 10 since gcd( j,k) = gcd(5,10) = 5, (but all smaller qualified k are coprime to j).
a(4) = 22 since gcd( j,k) = gcd(11,22) = 11, etc.
a(5) = 46 since gcd(23,46) = 23, etc.
a(6) = 94 since gcd(47,94) = 47, etc.
a(7) = 5 since gcd(95,5) = 5, etc., and we note that both j and k are composite.
a(8) = 2 since
gcd(6,2) = 2. We note that 2 has not appeared in a.
a(9) = 6 since
gcd(3,6) = 3.
a(10) = 14 since gcd(7,14) = 7, etc.
See Code 1 to generate A347113. We initially produced a 218-term dataset using an extensible form of this code that has been expanded incrementally to reach 219 = 524288 terms.
We present a summary of basic facts about the sequence.
- As a consequence of forbidden j = k and gcd(j, k) = 1, prime j implies j | k, therefore j < k. The least possible k > j such that j | k is 2j. Hence prime j | k yields k = 2j.
- Likewise, for prime k, that is, prime a(n), we have k | j, which implies j > k.
- Another consequence of forbidden j = k: local minima are nonadjacent, that is, terms A347757(m+1) − A347757(m) > 1.
- Let u(n) = A347755(n) be the least number that does not appear in a(1..n), and let r(n) = A347307(n) be a record. There are 3 regions with respect to prospective k;
- 1 < k < u is forbidden;
- u ≤ k ≤ r admits certain k, obviously including u but not r;
- all k > r may enter the sequence.
As a consequence, distinct terms in u constitute local minima in a; these appear in A347756(m) at a(A347757(m)).
- Local minima s in A347756 are prime except the trivial absolute minimum a(1) = s(1) = 1.
- Records r are the fruit of Cunningham chains p → 2p wherein multiple consecutive terms may set records.
- Because of the Cunningham chains, we see several apparently evenly-spaced linear features in the log-log scatterplot (Figure 1.2) above the line of a(n) = n.
- Cunningham chains appear in the tail (i.e., 1 or more final terms) of certain increasing runs.
- Having both j and k prime is disallowed, since j and k must be dissimilar primes. Dissimilar primes j and k are forbidden as they imply gcd(j, k) = 1, which is also disallowed.
General observations of interest, given 219 terms of a:
- Composite j | k yields k = 3j.
- Prime k | j = q such that j/q = p, p < q, both primes, in all cases except the first 3, i.e., a(7), a(8), and a(11), with (j, k) = {(95, 5), (6, 2), (15, 3)} respectively.
In other words, squarefree semiprime j = pq, p < q, yields k = q outside of the first 3 instances in this sequence. - There is 1 instance of composite k | j, i.e., a(33) = 25, with j = 75. Are there any others?
- Though it is possible that given prime j, 2j is already in a(1..n−1), this has not been observed.
- Furthermore, poorly divisible composite j may also yield 2j iff all j-noncoprime k < 2j are already in a(n). This has not been observed.
- However, is it possible that we might also see composite j → 2p? None have been observed.
- Aside from composite j | k, terms that involve neither j | k nor k | j cluster around a(n) = n in scatterplot except when the divisor is composite. Let “||” denote a | be with e > 1. The central group admits (j | k ∧ k || j) and the rare relation (j || k ∧ k | j). In other words, the terms in the central cluster are k such that 2 ≤ gcd(j, k) < min(j, k), including composite j | k and a(33), i.e., composite k | j.
What seems incredible are lines we see under a(n) = n, meaning the primes in a. These terms are the fruit of a fall. Why would these be arranged in seemingly linear rays?
The conclusion of this paper details findings that are summarized above.
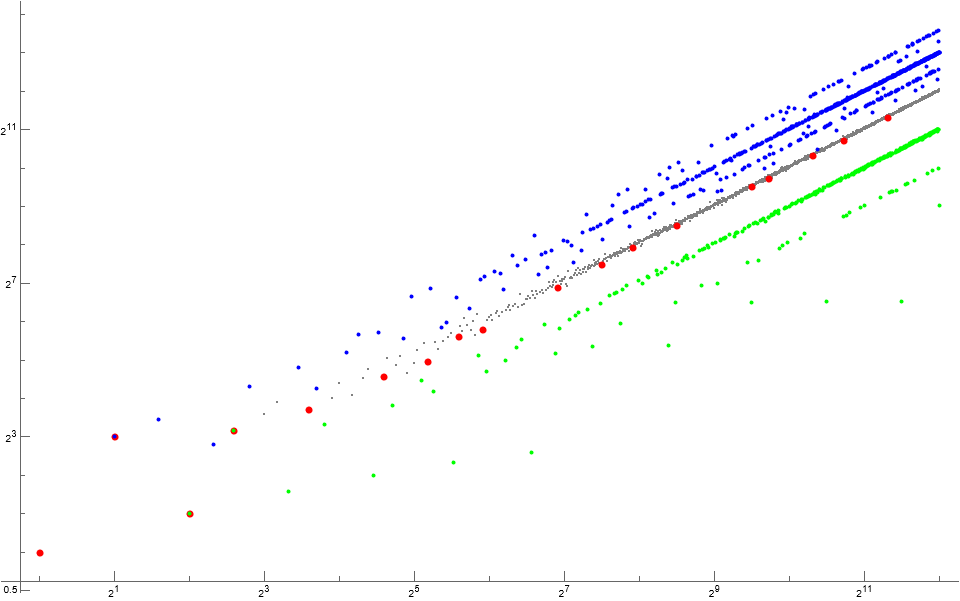
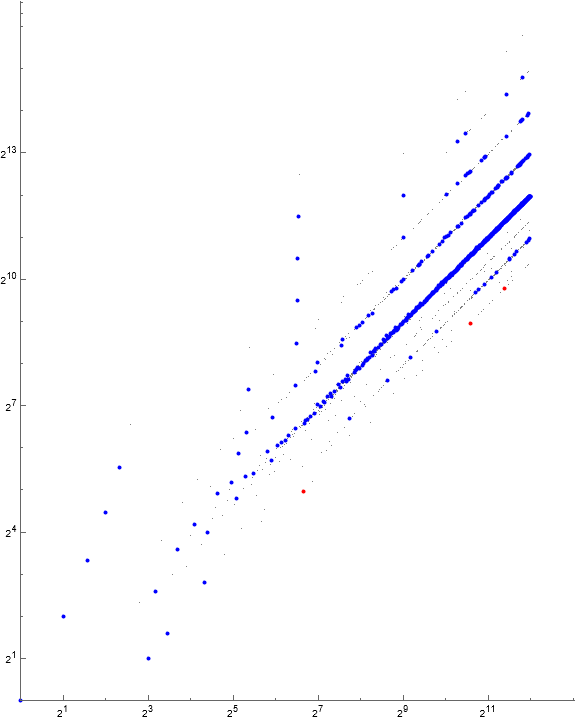
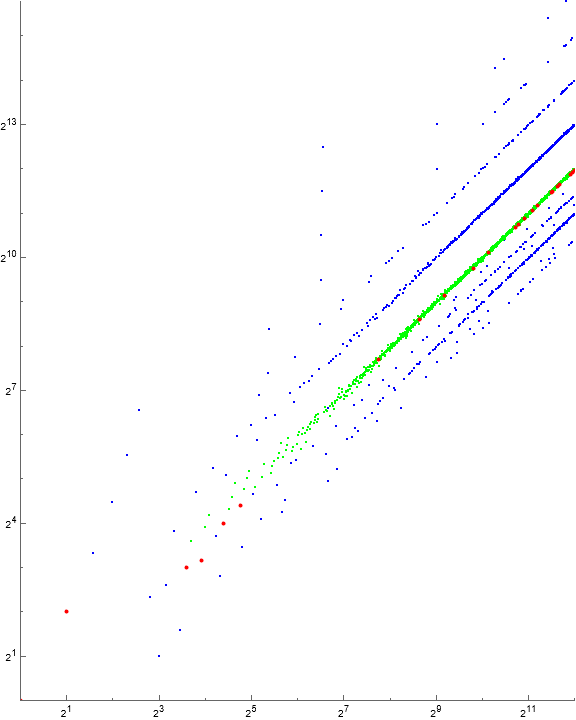
Figure 1.1 is a scatterplot of a(n) for 1 < n < 216, demonstrating quasi-radial linear features, with certain of these heavy. The “radial” arrangement induces us to use a logarithmic scatterplot from this point forward.
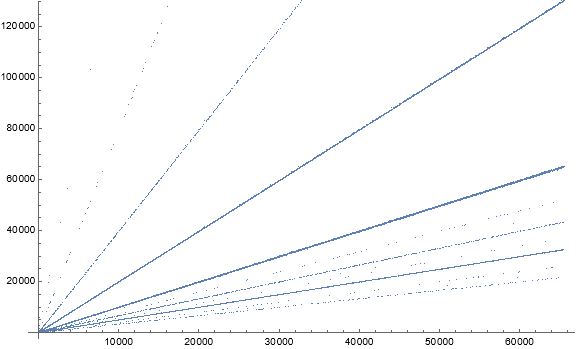
Figure 1.2 is a log-log plot of a(n) for 1 < n < 218, showing local maxima r in red, while local minima s appear in blue.
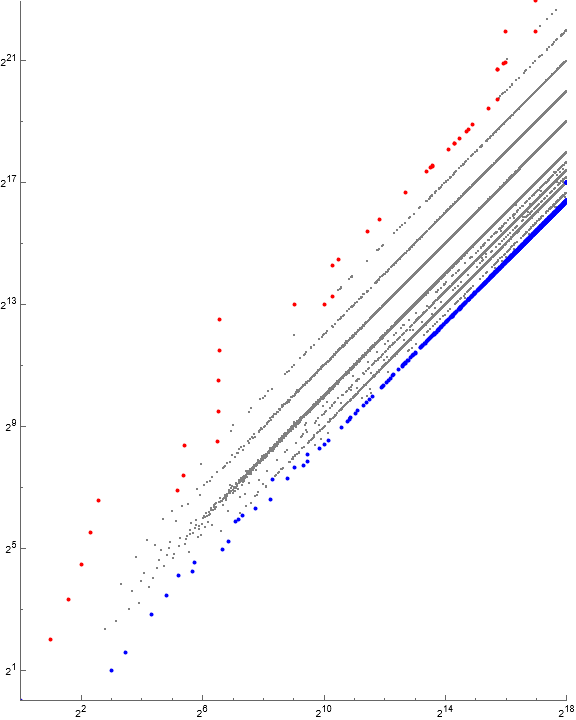
Figure 1.2 suggests perhaps that the quasi-radial lines in Figure 1.1 are perhaps instead quasi-exponential curves separated by a factor close to 2 in the case of the evenly-spaced features. Figure 1.3 suggests that the quasilinear features are reflections of points tightly arranged along the line n = a(n).
Therefore we shall refer to the points along the line n = a(n) = k as the “central group” and attempt to refine the definition.
Figure 1.3 is a log-log plot of a(n) for 1 < n < 216, emphasizing terms a(n) such that | a(n) − n | = 8 log n in large red points.
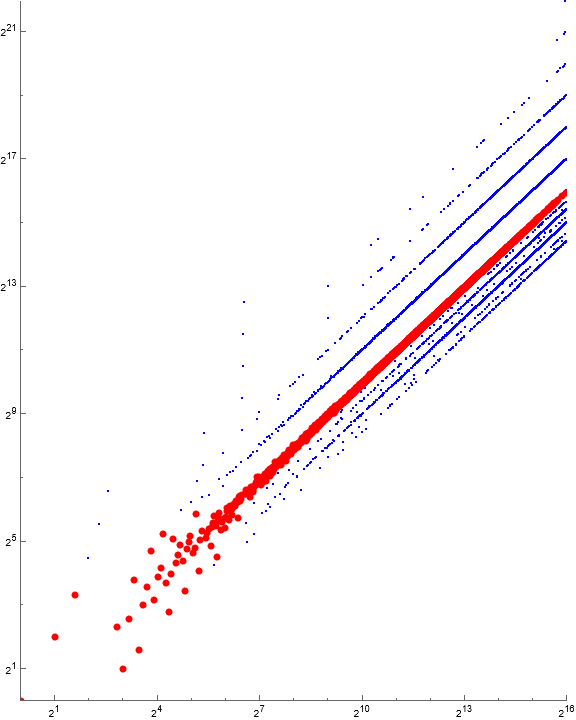
The inverse of a is t = A347306, which begins:
1, 8, 11, 2, 7, 9, 20, 12, 15, 3, 28, 13, 19, 10, 16, 21, 37, 17, 51, 23, 27, 4, 53, 24, 33, 14, 29, 34, 47, 25, 101, 30, 38, 22, 43, 31, 116, 18, 44, 39, 58, 45, 63, 48, 52, 5, 99, 49, 59, 54, 68, 60, 81, 55, 64, 50, 73, 35, 136, 56, 146, 26, 65, 69, 72, 66, 159, 74, 77, ...
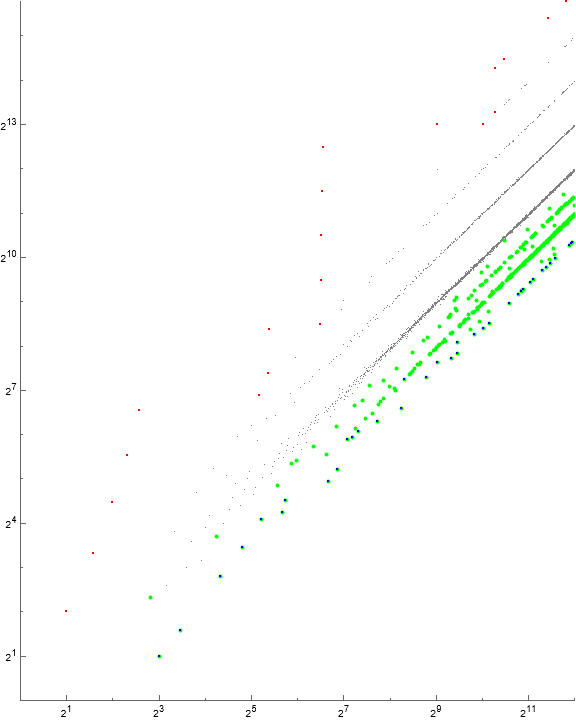
Prime k = pi is found at a(A347313(i)). Since primes must either divide or be coprime to another number and since coprimality is forbidden by definition of a, k | j implies j > k. Therefore prime k are the fruit of declining runs in a. In Figure 1.5, we see that the prime terms appear generally below the central group. All the local minima s outside of a(1) = s(1) = 1 are prime.
Figure 1.4 is a log-log plot of a(n) for 1 < n < 212, emphasizing in green terms a(n) = k prime.
Qualities of A347306:
t(p) > p prime, since prime p = k | j implies j > k.
t(q) < q for q = n/2 prime, since q = j | k implies j < k.
Hence, p appears generally above t(n) = n in scatterplot, while q appears generally below a(n) = n.
The scatterplot essentially sorts numbers into primes, n such that n/2 is prime, and all other n.
Figure 1.5 is a log-log plot of t(n) for 1 < n < 212, emphasizing in blue terms t(p) = k prime, and in green terms t(q) where q = n/2 prime. t(n) for highly composite n appear in red.
General properties of A347113.
Maxima and minima.
Maxima r = A347307(m) appear at a(A347308(m)), while local minima s = A347756(m) appear at a(A347757(m)). See Code 2.
The list r of maxima begins:
1, 4, 10, 22, 46, 94, 118, 166, 334, 358, 718, 1438, 2878, 5758, 8158, 8254, 9838, 19678, 22558, 43198, 56638, 103198, 169438, 184798, 190558, 193918, 274558, 315358, 318238, 357598, 419038, 439678, 486238, 698398, 858238, 1716478, 1723198, 1965118, 2029438, 4058878, 4068478, 8136958, 8577598, 9475198, 10909438, 12968638, 25937278, ...
These are found at the following indices:
1, 2, 3, 4, 5, 6, 36, 41, 42, 90, 91, 92, 93, 94, 519, 1044, 1251, 1252, 1422, 2748, 3591, 6528, 10685, 11661, 12028, 12236, 17326, 19899, 20074, 22571, 26429, 27702, 30538, 43975, 54016, 54017, 54229, 61703, 63862, 63863, 127935, 127936, 269513, 297679, 342675, 407267, 407268, ...
The records are even outside of the trivial first record 1, through the operation of Cunningham chains. Indeed, many terms are r such that j = r + 1 is prime. Those r such that j = r + 1 is composite represent the termination of a Cunningham chain.
The sequence a involves the recurrent mapping of the function f(x) = k ∉ a such that k ≠ j and gcd(k ,j) ≠ 1, where j = a(n−1) + 1, starting with the input 1. By definition all terms k in a are distinct and no non-positive terms k appear in a. The preclusion from repeating k ≥ 1 suggests that we may have a “least unused” number u(n). In other words, u(n) is the smallest positive integer that does not occur in a(1..n).
The sequence u = A347755 begins with u(0) = 1 since a(1) = 1 by definition:
1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 7, 7, 7, 7, 7, 7, 7, 7, 7, 11, 11, 11, 11, 11, 11, 11, 11, 17, 17, 17, 17, 17, 17, 17, 17, 17, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 19, 23, 23, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, 31, ...
Clearly the sequence u is tantamount to the local minima s since by definition these are the least gaps in coverage of a; when they are filled in, they set local lows. Local minima are set when the least unused u(n) = a(n + 1), thereafter, the sequence can only increase. Because k is distinct in a, and since by definition u(n) is the least number missing from a(1..n), distinct u(n) ∈ s.
We disambiguate between u(n) = A347755(n), the least positive number that does not appear in a(1..n), which may hold constant as n increases until some k = u(n), but generally is nondecreasing, and s(n) = A347756(n), which contains the distinct terms in u, that is, the local minima of a. (See Code 3.)
The sequence s = A347756 is a list tantamount to the sequence of local minima in a that begins as follows:
1, 2, 3, 7, 11, 17, 19, 23, 31, 37, 59, 61, 67, 79, 97, 151, 157, 199, 211, 229, 271, 307, 337, 367, 499, 577, 601, 619, 691, 727, 829, 877, 937, 1009, 1237, 1279, 1297, 1399, 1459, 1531, 1609, 1657, 1867, 2011, 2029, 2089, 2131, 2137, 2179, 2281, 2311, 2467, 2539, ...
We may find the first indices of s(i+1) in u, which is equivalent to the indices n of the local minima s(i) in a. We store these indices in S = A347757:
1, 8, 11, 20, 28, 37, 51, 53, 101, 116, 136, 146, 159, 213, 302, 318, 440, 520, 638, 698, 702, 912, 1031, 1128, 1528, 1758, 1832, 1891, 2107, 2198, 2523, 2671, 2857, 3069, 3760, 3892, 3946, 4256, 4438, 4638, 4880, 5022, 5656, 6092, 6147, 6322, 6470, 6492, 6579, ...
Table 2.1 lists the i-th record a(n) = r and the i-th local minimum a(n) = s.
i n r n s
--------------------------------
1 1 1 1 1
2 2 4 8 2
3 3 10 11 3
4 4 22 20 7
5 5 46 28 11
6 6 94 37 17
7 36 118 51 19
8 41 166 53 23
9 42 334 101 31
10 90 358 116 37
11 91 718 136 59
12 92 1438 146 61
13 93 2878 159 67
14 94 5758 213 79
15 519 8158 302 97
16 1044 8254 318 151
17 1251 9838 440 157
18 1252 19678 520 199
19 1422 22558 638 211
20 2748 43198 698 229
21 3591 56638 702 271
22 6528 103198 912 307
23 10685 169438 1031 337
24 11661 184798 1128 367
...
Let m be the initial k generated by the function f(a(n)) such that gcd(k, j) > 1. We may divide the range 1 ≤ m of the function f into three segments based on membership of m in a:
- m > r where r is the most recent record. Such m are novel to a and generate a(n+1).
- m < u where u is the least gap in a. Such m are extant in a and necessitate k > m such that gcd(k, j) > 1.
- u ≤ m < r. In this band, we have an increasing chance of finding novel k as m increases, certainly with the cases that m = u yields a novel k, and m = r yields and extant k and necessitates further search.
- There is a significant difference in available gaps between the lower u ≤ m ≤ n and upper n < m < r given the density of terms in the central group, especially as n increases. The upper band is rarified while the lower band is more saturated.
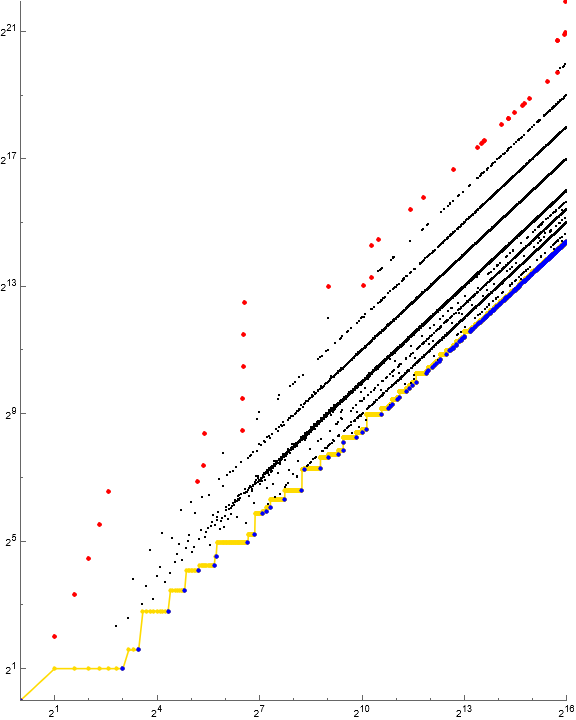
Figure 2.1: We can indicate u on a log-log scatterplot of a(1… 212). The records and local minima appear in red and blue, respectively, while u = A347755 is plotted gold. See Code 8.
Parity.
Let E(n) = A347312(n) = a(n) mod 2. The sequence begins as follows:
1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, ...
The scatterplot seems to indicate a stark bifurcation roughly along the line a(n) = n. We shall return to parity and the appearance that the sequence cleaves according to parity.
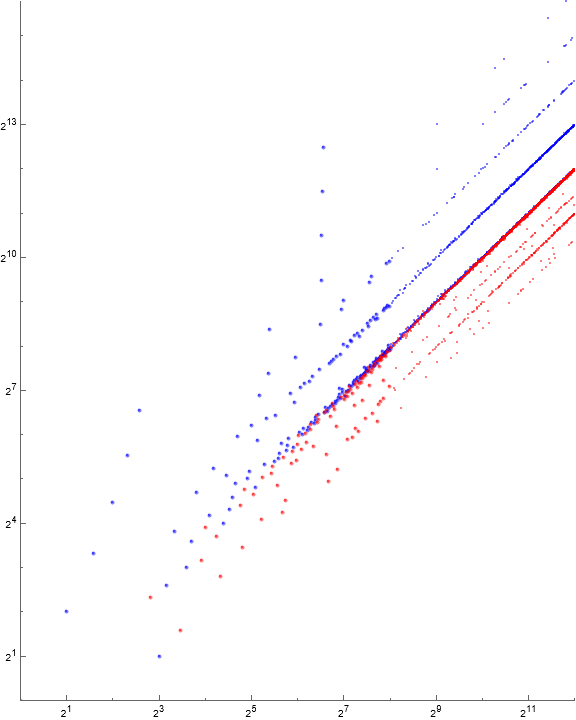
Figure 2.2 is a scatterplot of a(n) for 1 ≤ n ≤ 212 showing even k in blue and odd k in red.
Ratio j/k.
The consequence of the prohibition of j-coprime k and j = k include that k ≡ 0 (mod j) iff j < k and that k may not be in the reduced residue system of j. As regards the ratio j/k, through simplification N/D, we may have integer ratios for j < k, and unit fractions for j > k.
Table 2.2 lists various ratios j/k seen the dataset a(n) for 1 ≤ n ≤ 219, the number of these ratios in the dataset, the index n of the first instance of j/k, the values j and k = a(n), and the constitutive states seen that pertain to the ratios (which will be explained in section 4). The ratio “Other” includes any j ≡ m (mod k) or k ≡ m (mod j) for m ≠ 0.
Ratio card. n a(n-1)+1 a(n) states
------------------------------------------------------
other 453866 13 9 12 0, 2, 6
1/2 46959 2 2 4 3, 5
2 17897 20 14 7 1
3 4424 8 6 2 1, 7
5 542 11 15 3 1
2/3 225 16 10 15 0, 2
7 158 37 119 17 1
1/3 96 102 32 96 3
2/5 56 703 272 680 6, 8
11 40 440 1727 157 1
13 9 1923 15119 1163 1
17 4 1423 22559 1327 1
29 3 12029 190559 6571 1
31 2 397131 6323039 203969 1
19 2 7 95 5 1
47 1 144506 4595519 97777 1
41 1 520 8159 199 1
37 1 269514 8577599 231827 1
23 1 113529 1806719 78553 1
1 1 1 - 1 (9)
Integral ratios pertain to increase, fractional to decrease. The other offset ratios pertain to ambidirectional states explained in section 4.6.
Towers.
Through observation, the default case of poorly divisible j is to have k = 2 j, hence the “spacings” seem to be doublings of j, i.e., a(n+1) = 2(a(n) + 1). The two conspicuous red “towers” lend some creedence to the conjecture. The first evident “tower” has 1 → 4 → 10 → 22 → 46 → 94 = A033484(0…5) = 3(2n) − 2. The second has 358 → 718 → 1438 → 2878 → 5758, which has the same recurrence signature (3, −2). It seems we see the towers whenever there are recurrent occasions of prime j, meaning (a(n) + 1) prime. A composite k breaks the tower-cycle in both cases.
Composite j as an obstacle to tower cycles.
Is it true that composite j will always break cycle?
The least k ≠ j, with j prime, such that gcd(j,k) > 1, is 2j. For composite j, p | j, with p the least prime factor of j is the smallest k such that gcd(j,k) > 1. The more factorable j present many divisors, and indeed, many numbers neutral to j, such as numbers r | je with e ≥ 2, and numbers s such that s is the product of at least one p | j and at least one prime q that does not divide j. This is to say that j-noncoprime k are eligible to enter a so long as they do not already appear in a. For instance, j = 12 presents {2, 3, 4, 6, 8, 9, 10, 14, 15, 16, 18, 20, 21, 22, 24, …}. It seems unlikely that sufficiently composite numbers would prevent the sequence from decreasing, because for any composite j > 4, the number of potential k < j exceeds τ( j) − 2, and many of these potential k would still be available. However, the factors of highly divisible numbers m, along with nondivisor regular numbers of same tend toward commonly produced small m themselves. The actual k generated by sufficiently factorable j doesn’t seem predictable.
It would seem that there are chances for certain composite j, say, sufficiently large squarefree semiprimes j = pq with p = (q − 2), so as to minimize the chance that the factors of such are novel to a. Indeed, suppose the factors already in a as well as the semidivisor p² < pq. We see that pq < q² < 2pq, a squared factor that is a pq-semidivisor. In cases where p ≠ 2, 2pq is pq-semicoprime, otherwise 2pq = p²q; both are pq-neutral. Also, products of primes p, q and r where gcd(pq, r) = 1 abound as pq increases. In later study we come to find that semiprimes j = pq in particular instead yield prime k, which implies j > k, hence cannot form anything beyond the “base” of the tower.
In order for k = 2pq, we must have all of {p, q, p², q²} extant in a, as well as any product m < 2pq of at least one of {p, q} and prime r coprime to pq. Outside of 2² = 4 = a(2), p² is ever less likely to enter a before p, since the multiples 2p, 3p, 4p, etc., must be consumed and placed in a. The only way a perfect prime power pe may enter a is by means of j = mp, i.e., a(n) = mp − 1 and for some integer m, once all pε with ε < e are consumed. We observe that 2p appears in a ahead of p for all p as a result of the the tower-cycle process involving prime j = p, f(p) = 2p itself. Rarely do we have 3p ahead of p (primes such that p appears after 3p in a: 29, 359, 997, 2003, 2129, 2131, 3181, 3593, 4561, 4603, 4817, 5531, 7559, …). Therefore it may be possible that some poorly factorable composites k might trigger the doubling tower cycle k = 2 j, but ever more unlikely as their prime factors increase. None have been observed given 219 terms of a.
Prime j as the engine behind tower cycles.
Is it true that prime j = p will always perpetuate the cycle so as to produce a Cunningham chain? We know that by definition of f, j ≠ k, that is terms in a are distinct by definition. This means that we cannot have the same seed p for recursive mappings of f(p) = mp, hence the tower-cycles that appear in a are also distinct. The least k > p that is not coprime to p is 2p. Therefore f(p) = mp, m ≥ 2. Hence, the tower cycle will always be continued by prime j = p, however it is possible that a factor m > 2 accelerates tower growth. The appearance of prime j = p always presents f(p) = 2p in a(n) for n ≤ 219. Is there a case where prime j = p always presents f(p) = 3p? We do observe j/k = 3 in a, but this pertains to composite j in all cases. Therefore, we will call the tower building phenomenon a “duplation cycle”.
By definition, j = p is distinct in a, hence any Cunningham chain is also distinct along with any of its terms 2p, 2(2p + 1), etc.
It appears there is a tower-building phase that forms part of the increasing runs in a, and a collapse phase that does not prove as strong, governed by the least unused u. This is in actuality complicated by many terms that do not deviate far from the line defined by a(n) = k = n. The tower building phases evident in the striations k > n represent only a small but conspicuous fraction of all terms in a, and the striations k < n are even smaller in relative number.
Increase and Decrease.
Let the sequence d be that of the first differences of a. (See Code 4.)
3, 6, 12, 24, 48, -89, -3, 4, 8, -11, 5, 4, 14, -17, 6, 3, 20, -25, -6, 9, 18, -14, 4, 6, 32, -41, -10, 16, 5, 4, 38, -49, 3, 30, 60, -101, 16, 7, 42, 84, 168, -299, 4, 3, 44, ...
Then the sequence D, which is 1 if d(n) positive, else 0, prepended by 1, constitutes the characteristic of increase. (See Code 4.)
1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, ...
By this we might take run lengths ℓ:
6, 2, 2, 1, 3, 1, 3, 2, 2, 1, 3, 2, 4, 1, 3, 1, 5, 1, 3, 1, 3, 1, 1, 1, 4, 1, 4, 1, 4, 1, 3, 2, 3, 1, 3, 1, 2, 1, 1, 1, 8, 2, 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 3, 2, 4, 1, 2, 1, 4, 2, 4, 2, 5, 1, 2, 2, 4, 1, 1, 1, 4, 2, 2, 1, 2, 2, 2, 1, 5, 2, 5, 1, 2, 1, 2, 1, 5, 1, 1, 2, 3, 1, ...
From this it is easy then to determine the nature of increase and decrease in a as n increases. (See Code 5.)
Figure 3.1 is a scatterplot of a(n) for 1 ≤ n ≤ 210 with increasing runs joined by red lines, terminating in a high marked by a large red dot, and decreasing runs joined by blue lines, terminating in a low marked by a large blue dot. The first segment after the cusps are not joined for clarity.
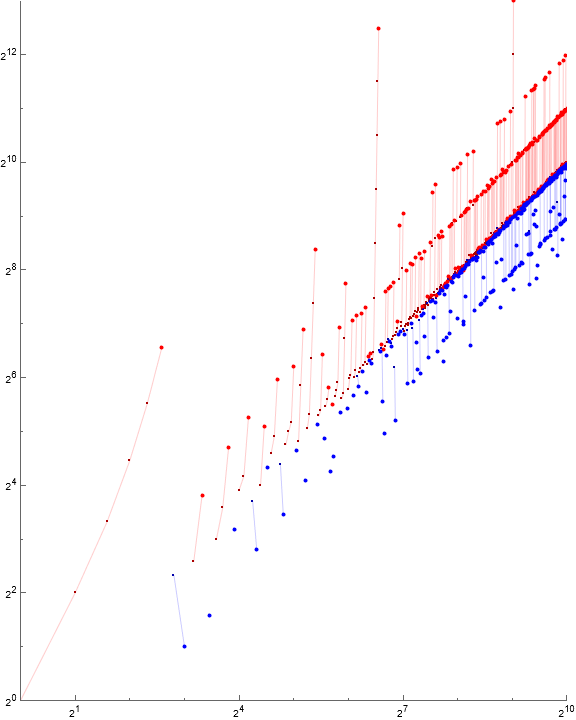
Figure 3.1 suggests that the initial move from a high or low cusp regresses the function toward the central group. From there, of course, the increases take the function toward records (not always setting them) or local minima (also not always setting them).
Therefore the first terms of the increasing runs and those of the decreasing runs are of interest.
Let H(i) be the i-th increasing run and L(i) be the i-th decreasing run.
Table 3.1 lists the first 21 rows of H:
1 {1, 4, 10, 22, 46, 94}
2 {6, 14}
3 {8, 12, 26}
4 {15, 18, 38}
5 {16, 34}
6 {24, 30, 62}
7 {27, 32, 36, 74}
8 {28, 58, 118}
9 {33, 40, 82, 166, 334}
10 {39, 42, 86}
11 {44, 48, 56}
12 {45}
13 {50, 54, 60, 122}
14 {49, 52, 106, 214}
15 {55, 63, 66, 134}
16 {64, 70, 142}
17 {68, 72, 146}
18 {75, 78, 158}
19 {76, 84}
20 {87}
21 {81, 88, 178, 358, 718, 1438, 2878, 5758}
...
Table 3.2 lists the first 21 rows of L:
1 {5, 2}
2 {3}
3 {9}
4 {13, 7}
5 {20}
6 {21, 11}
7 {25}
8 {17}
9 {35}
10 {29}
11 {19}
12 {23}
13 {41}
14 {43}
15 {51}
16 {65, 57}
17 {69}
18 {53}
19 {80}
20 {77}
21 {91, 90}
...
Duplation phases.
We see that there are some singleton increasing runs but such seem more prevalent among decreasing runs. Furthermore, it seems that the increasing runs tend to be longer. Reason supports a less restricted length of increasing runs.
Table 3.3 is a list of the least index n ≤ 218 of an increasing run H of length ℓ, showing a duplation phase in bold:
ℓ n H
---------------------------------------
1 52 {45}
2 9 {6, 14}
3 12 {8, 12, 26}
4 29 {27, 32, 36, 74}
5 38 {33, 40, 82, 166, 334}
6 1 {1, 4, 10, 22, 46, 94}
7 3545 {3485, 3489, 3495, 3500, 3504, 3510, 7022}
8 87 {81, 88, 178, 358, 718, 1438, 2878, 5758}
9 61695 {61269, 61276, 61306, 61408, 122818, 245638, 491278, 982558, 1965118}
...
Firstly, extension of a beyond the most recent record r admits any k since by definition of record, all k > r are novel. Contrast this to the increasingly rarified availability of gaps as k decreases toward u. For k < u, there are no available gaps.
Secondly, for j = prime p, f(p) = k = 2p, since 2p is the least k such that gcd(k,p) > 1. The term 2p is novel to a since the least number k such that gcd(k, j) > 1 must have at least one prime divisor in common with j. Semiprime 2p may only enter a via j = 2 or j = p. Considering j = 2, we see 2 j = 4 enter at a(2) because there was no other means by which 4 was the least available k on account of factors (and of course, a(2) is a special case following the given term). It is evident that for a(n−1) = (p−1) we see a(n) = 2p since we might only see 2p enter otherwise through a repetition of the appearance of 1 in the sequence, which is forbidden. Hence 2p may enter the sequence solely after the appearance of (p−1).
This implies that prime j = p necessitates increase since 2p always follows (p−1) in a.
Thirdly, a “duplation phase” may emerge that involves a finitely recurrent mapping of f(p) = k = 2p, provided k = 2p = (q−1) for some prime q. We would be correct in saying the duplation phase is a Cunningham chain if all the terms in the chain are prime. Such a chain breaks upon arriving at k such that k+1 is composite. This is because a composite j has relatively small k such that gcd(k, j) > 1 available. It may stand that certain poorly divisible composite k might yield k = 2p as well, however we know that squarefree semiprime j cannot be the source of these poorly divisible composite j.
Therefore we should see records in a achieved by means of at times particularly protracted chain-building.
Figure 3.2: scatterplot of a(n) for 1 ≤ n ≤ 212 showing integer factors m involved in increase mj = k > j. Blue signifies m = 2, while red signifies m = 3. We shall show that m = 2 pertains to prime j, while 3 pertains to certain composite j.
Mediation phases.
Table 3.4 is a list of the least index n ≤ 218 of a decreasing run L of length ℓ, showing a mediation phase in italic and a division (a(n)+1)/3 in italic.
ℓ n L
------------------------------
1 11 {3}
2 7 {5, 2}
3 291 {287, 279, 275}
4 581 {578, 573, 553, 277}
5 15544 {15404, 15399, 15389, 15371, 15311}
6 87862 {87395, 87273, 87263, 87163, 86881, 43441}
...
The term “mediation” is not completely appropriate, since mediation by definition represents division by 2, yet the factors take many distinct prime values. For a(n) with n ≤ 219, we see the following prime factors:
Table 3.5 is a list of prime r = j/k seen in a(n) for 1 ≤ n ≤ 219 in mediation phases that produce a series of striations in the scatterplot where k < n. The column n is the smallest index such that a(n−1)+1 = j and a(n) = k have the ratio j/k = r. The number c of mediation terms with ratio r seen in a(n) for 1 ≤ n ≤ 219appears in the last column.
r n j k c
-----------------------------------
2 20 14 7 17897
3 8 6 2 4424
5 11 15 3 542
7 37 119 17 158
11 440 1727 157 40
13 1923 15119 1163 9
17 1423 22559 1327 4
19 7 95 5 2
23 113529 1806719 78553 1
29 12029 190559 6571 3
31 397131 6323039 203969 2
37 269514 8577599 231827 1
41 520 8159 199 1
(43) - - - -
47 144506 4595519 97777 1
...
The primes r in Table 3.5 represent the least prime factor p of squarefree semiprime j = pq, p < q for n > 11, since k = q. For mediations seen at a(7), a(8), and a(11), that is, j/k = 95/5, 6/2, 15/3, respectively, the situation is reversed. This is the reason why r = 19 appears early; it resulted from the first termination of a Cunningham chain by composite 95. Therefore, for all other mediations, we see the least prime factor of a distinct squarefree semiprime. Hence we anticipate that r = 43 will appear, as will r = 53, 59, etc., not necessarily in order, yet smaller prime r will prove generally more common the smaller we consider r. When will r = 43 appear?
Inflexion Points.
Let the sequence η include all indices n of a(n) that start an increasing or decreasing run. Certainly we can have ηH and ηL for increasing and decreasing runs, respectively. The terms a(n) for n in η therefore represent inflexion in the sequence. We may then survey the nature of the terms so as to attempt to determine what caused change. (See Code 5.)
Sequence η begins:
(1,) 6, 8, 10, 11, 14, 15, 18, 20, 22, 23, 26, 28, 32, 33, 36, 37, 42, 43, 46, 47, 50, 51, 52, 53, 57, 58, 62, 63, 67, 68, 71, 73, 76, 77, 80, 81, 83, 84, 85, 86, 94, 96, 97, 99, 100, 101, 103, 104, 106, 108, ...
(We may prepend 1 by convention.)
We already know that prime j = p induce increase via f(p) = mj, m ≥ 2. The increasing runs terminate with composite (k + 1) in all 144729 full cases for n ≤ 219. In examination of the constitutive relations between j and k to be discussed below, we find that the inflexion points take any state admissible for increase and decrease respectively, therefore, the relation of j and k (e.g., j | k, etc.) cannot be used to judge why a given inflexion occurs.
The least j-noncoprime k ≠ j must be greater than or equal to u, the least unused number. Therefore, for highly divisible numbers, k is not easy to predict. For prime j, k = 2j, generating a Cunningham chain only to collapse upon composite j. This however does not explain inflexions amid neutral states, i.e., those where 1 < gcd(j,k) ≠ ( j or k).
Similarly, decreasing runs, stunted by rarification of available gaps as k approaches u, draw to a close upon squarefree semiprime j yield a prime k. It is not known whether this is always the case, but holds for n ≤ 219
We plan to explore the nature of inflexion at a later date. Some exploration of inflexion appears in the discussion of constitutive signatures associated with increase and decrease.
Group γ and the second term of directional runs.
Figure 3.1 seems to show a “herringbone” effect that suggests increase and decrease stem from the central group (i.e., group γ), however, we had eliminated line segments that join the inflexion point and the second term of the runs so as to clarify the plot.
Such a plot leads us to consider where the second term falls in the scatterplot, in terms of groups. For 219 terms in a, 95599 are second terms in directional runs. Group α comprises 753 terms, central group γ has 94721 terms, and group β has 125 terms. In contrast, 180565 inflexions appear in group α 26351 times, and in the central group 225878 times, while 14953 second terms appear in group β. Therefore it is true that the second terms of directional runs tend to appear in the central group.
Table 3.6 summarises the number of first (inflexion) and second terms in various groups.
Inf. 2nd
----------------------
Total 289459 152817
alpha 40677 1044
gamma 225878 151594
beta 22904 179
Constitutive analysis of { j, k}.
In the function f(x), we are dealing with gcd( j, k) > 1 shown in A347309, involving multiplicative properties of j with respect to k. Bear in mind that j coprime to k (i.e. j ⊥ k) is forbidden, and that j ≠ k by definition of the sequence. Unlike the other constitutive relations, j ⊥ k is symmetric; if j ⊥ k, then k ⊥ j. (The symbol ⊥ we attribute to Don Knuth, we employ || to mean regular under similar considerations as Knuth made for the perpendicular symbol used to mean coprime.)
Let us recognize three mutually exclusive, assymetric properties of any nonzero positive integers j and k, j ≠ k, gcd( j, k) > 1:
- j | k; gcd( j, k) = j. The expression j/k = m yields an integer.
- j | ke for e > 1. In other words, j is a semidivisor or nondivisor regular of k. We shall abbreviate k-semidivisor j as j || k. The expression j/k = m yields a rational number that is not an integer wherein the numerator and denominator n/d are such that n < j and m < d. A regular number j with respect to k has distinct prime divisors p that are a subset of those of k, and contains no prime factor q that does not also divide k.
- j is the product of at least one prime p | k and at least one prime q that does not divide k. In other words, j is semicoprime to k. We might also say j is nonregular and neutral to k. We shall abbreviate k-semicoprime j as j ◊ k. The expression j/k = m yields a rational number that is not an integer wherein the numerator and denominator n/d are such that n < j and m < d.
(The “constitutive” properties of pairs of nonzero positive integers are described in [1])
Cases 2 and 3 represent “neutral” relationships (meaning that j neither divides nor is coprime to k) [2] and pertain to j and k that are both composite [3], while Case 1 may pertain to any nonzero positive pair of numbers. We recognize that j | k is a special case of j || k, but here shall only use the latter notation to pertain to nondivisor regular j | ke for e > 1.
Divisibility and Directionality.
Through [3], we know that prime j = p necessitates j < k and j | k since the alternative is not available. Likewise, if we see k | j, then j > k since all terms in a are distinct by definition. We tend to see:
Prime j: f( j) = 2j, i.e., Cunningham chains,
Prime k: j = pq, p < q, distinct primes; f(pq) = p for n ≤ 11 and q for n > 11.
We also have mappings of f(x) for composite x that do not involve divisors and are thus not constrained by the exclusion of coprimality.
Bisection of a by means of constitutive relationships between j and k.
We know that j | k does not necessitate k | j; indeed j | k and k | j are both true iff j = k, since in order for one number to divide the other, the former may not exceed the latter. Similarly, j | ke for e ≥ 0, that is k-regular j does not necessitate j-regular k. Indeed k-regular j and j-regular k both true iff rad( j) = rad(k), that is, if and only if j and k share the same squarefree kernel. It is often the case that while we have k-regular j, k may have at least 1 factor q that does not divide j. We note that j | ke for e > 1 iff both j and k are composite, since prime j may only divide k otherwise j may only fall into Case 3, both as far as sequence a is concerned. Finally, j ◊ k may be k-regular as already discussed.
For prime j, we must have k = 2j such that gcd( j, k) ≠ 1. If j = 2, then k = 4, 2 | 4 and 4 || 2, but otherwise j | 2j and 2j ◊ j (on account of the former even and the latter odd by definition). If 2j is already in the sequence, then we move to 3j, etc.
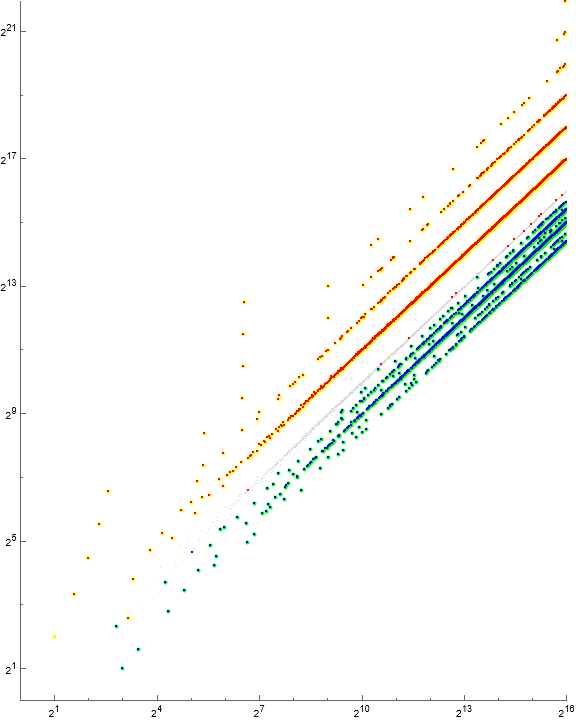
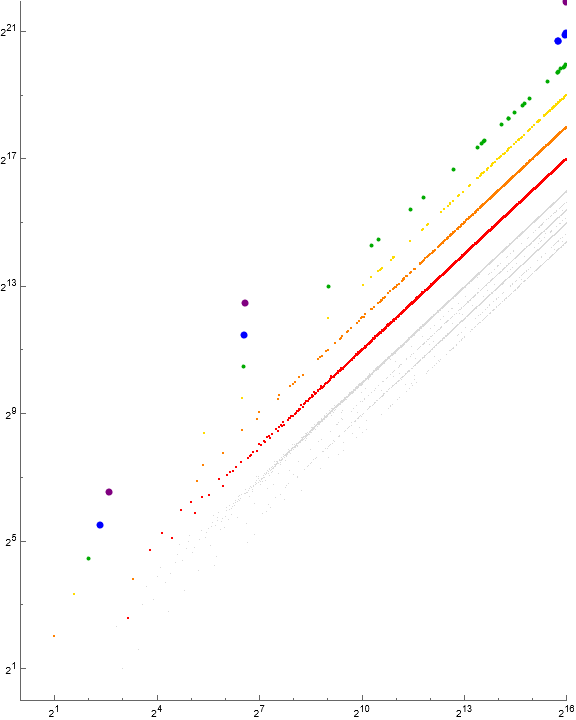
Figure 4.1 is a scatterplot of a(n) for 1 ≤ n ≤ 212 showing j | k in red, j || k in green, and j ◊ k in blue. Prime j is highlighted in yellow.
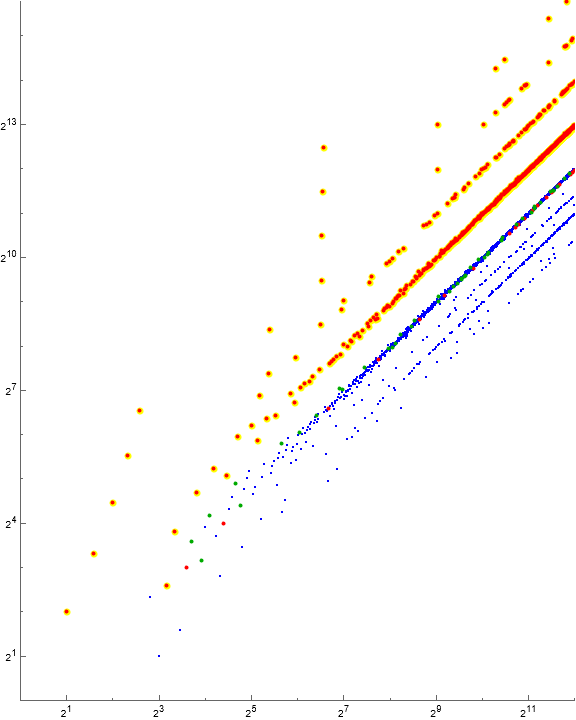
Figure 4.1 suggests that prime j = p is associated with p | k via f(p) = 2p. Aside from a(9) = 6 for which j = 3, prime j occurs above the central group in Figure 3.1. Therefore, it seem that nearly all k > n pertains to prime j, for k “sufficiently larger” than n. Further, j || k seems to occur only within the central group, while j ◊ k occurs in the central group and for k “sufficiently smaller” than n.
Let c(n) = −1 if j ◊ k, 0 if j | k, or 1 if j || k. Similiarly, c'(n) = −1 if k ◊ j, 0 if k | j, or 1 if k || j. We may define a sequence C(n) = 3×(c(n)+1) + (c'(n)+1) and thereby derive 9 possible states into which {j, k} might fall (see Code 6), as shown by Table 3.1:
Table 4.1: states of the constitutive relationships of j and k in sequence a:
| | | j ◊ k | j | k | j || k | |
| ------- | | | ------- | ------- | ------- |
| k ◊ j | | | 0 | 3 | 6 |
| k | j | | | 1 | (4) | 7 |
| k || j | | | 2 | 5 | 8 |
We cannot have state 4 as mentioned above because j and k are distinct by sequence definition. We also define C(1) = 9 by definition, as a(1) is given by directive, therefore the state 9 is used merely as a placeholder. Table 4.3 gives an example of each constitutive relationship or state in the final column.
States 0, 4, and 8 are symmetrical; 0 is the symmetrically semicoprime state, state 4 symmetrically divisible state, and 8 symmetrically semidivisible.
Since we say a state is neutral if it involves j neither dividing k nor coprime to k, we have completely neutral states in 0, 2, 6, and 8, which require both j and k to be composite. Only j- and k-divisor states 1, 3, 5, and 7 that include j | k or k | j may have a prime j or prime k respectively. Since state 4 is forbidden, both j and k prime is also impossible.
We say a state is regular iff either j | ke or k | je with e ≥ 0. As a consequence of mutually regular relationships, j and k require the same squarefree kernel K. Therefore, we have completely regular states in 4, 5, 7, and 8, with 4 of course forbidden, and 8 completely semidivisible. Since state 8 is both completely regular and completely neutral, j and k must have the same squarefree kernel K and neither j nor k may be prime.
Since j | k implies j < k and therefore, sequence increase on account of a prohibited state 4, states 3 and 5 imply increase. Conversely, since k | j implies j > k and therefore, sequence decrease on account of a prohibited state 4, states 1 and 7 imply decrease. We call these directional states.
We find that the completely neutral states that are not also completely regular, i.e., states 0, 2, and 6, are ambidirectional. Though the symmetrically semidivisible state 8 does not prohibit j > k, such hasn’t been seen and may not appear on account of the mechanics of A347113. State 0, the symmetrically semicoprime state, represents the least order since gcd(j, k) may be as low as p prime. State 0 is the commonest state in a.
Ambidirectional states pose an obstacle against a streamlined algorithm to generate A347113, especially given the predominance of the condition, because we cannot predict the behavior of terms in such states.
We may therefore employ constitutive analysis to terms in a and relate these with parity, directionality, and the ratio j/k so as to better explain the sequence, to form conjectures, and to attempt proofs.
Table 4.2: List of C(n) for 2 ≤ n ≤ 24, showing associated j and k.
n C(n) j k
----------------
2 5 2 4
3 3 5 10
4 3 11 22
5 3 23 46
6 3 47 94
7 1 95 5
8 1 6 2
9 3 3 6
10 3 7 14
11 1 15 3
12 5 4 8
13 6 9 12
14 3 13 26
15 7 27 9
16 0 10 15
17 6 16 18
18 3 19 38
19 1 39 13
20 1 14 7
21 5 8 16
22 3 17 34
23 0 35 20
24 0 21 24
...
Table 4.3 lists the least index n for which j and k have the constitutive relationship C.
C n j k gcd number num.even
-------------------------------------------
0 16 10 15 5 453568 236174 10 ◊ 15 ∧ 15 ◊ 10.
1 7 95 5 5 23083 1* 95 ◊ 5 ∧ 5 | 95.
2 29 12 27 3 319 26 12 ◊ 27 ∧ 27 || 12.
3 3 5 10 5 45544 45544* 5 | 10 ∧ 10 ◊ 5.
4 . . . . impossible (j | k ∧ k | j iff j = k)
5 2 2 4 2 1511 1511* 2 | 4 ∧ 4 || 2.
6 13 9 12 3 246 224 9 || 12 ∧ 12 ◊ 9.
7 15 27 9 3 2 0* 27 || 9 ∧ 9 | 27.
8 1127 440 1100 220 14 14 440 || 1100 ∧ 1100 || 440.
The most frequent state is 0, that is j ◊ k and k ◊ j. State 7 occurs at a(15) involving 27 || 9 but 9 | 27, and a(26) involving 63 || 21 but 21 | 63, but never again for n ≤ 219. State 8, the symmetrical regular state, is a little more common, found at the following indices:
1127, 4461, 11711, 39353, 98460, 110105, 128788, 164689, 177668, 191234, 313559, 374665, 475094, 507283, ...
We regard the parity of terms in the various states. The states {0, 2, 6, 8} are ambidirectional, and we see also that at least the first 3 states may be either even or odd. State 8, symmetrically nondivisor-regular, implies both j and k composite; the state perhaps requires both to be even; Table 4.4 shows this, however there is technically nothing restricting odd terms. The implicitly-increasing states 3 and 5 are always even, though there doesn’t seem to be a prohibition for the latter against oddness. We recognize that states 3 and 5 have j | k with k necessarily neutral, and that it may only be a relatively empty distinction that state 3 involves k ◊ j while state 5 instead k || j. The implicity-decreasing state 1 is always odd except for the case of a(8) = 2, and always prime except for the case of a(33) = 25. The 2 terms in state 7 are both odd.
Table 4.4 lists occasions where j || k and k || j for 2 ≤ n ≤ 219, listing the distinct prime factors necessarily common to both j and k.
n j k Distinct prime factors
------------------------------------------------
1127: 440 1100 2, 5, 11
4461: 1760 4400 2, 5, 11
11711: 4640 11600 2, 5, 29
39353: 15620 39050 2, 5, 11, 71
98460: 39140 97850 2, 5, 19, 103
110105: 43760 109400 2, 5, 547
128788: 51200 128000 2, 5
164689: 65480 163700 2, 5, 1637
177668: 70640 176600 2, 5, 883
191234: 76040 190100 2, 5, 1901
313559: 124760 311900 2, 5, 3119
374665: 149120 372800 2, 5, 233
475094: 189140 472850 2, 5, 7, 193
507283: 201980 504950 2, 5, 10099
...
Figure 4.2 is a scatterplot of a(n) for for 1 ≤ n ≤ 216 that applies a color function associated with C. Blue indicates C = 0 (j ◊ k, k ◊ j), purple C = 1 (j ◊ k, k | j), dark cyan C = 2 (j ◊ k, k || j), magenta C = 3 (j | k, k ◊ j), large gold C = 5 (j | k, k || j), large cyan C = 6 (j || k, k ◊ j), large orange C = 7 (j || k, k | j), and large green C = 8 (j || k, k || j). See Code 9.
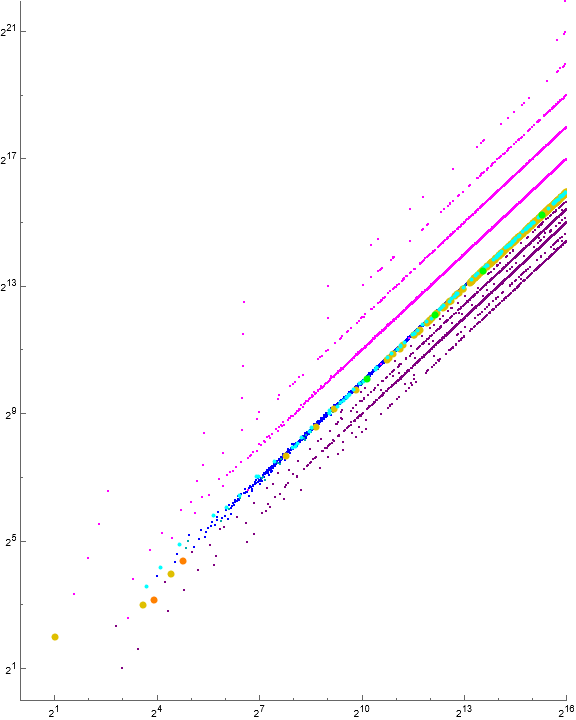
Figure 4.2 seems to sort the scatterplot by constitutive relationships.
Generally, k > n involves C = 3 (j | k, k ◊ j), while k < n involves the converse C = 1 (j ◊ k, k | j), with the other relationships falling along the central group.
Division of a into three groups based on divisibility.
With this sorting we now might divide the sequence into three groups (see Code 7):
- Group α that contains a(n) such that C(n+1) = 3, i.e., (j | k ∧ k ◊ j), k generally larger than n,
- Group β that contains a(n) such that C(n+1) = 1, i.e., (j ◊ k ∧ k | j), k generally smaller than n,
- The central group γ containing a(n) such that a(n+1) does not involve j | k or k | j.
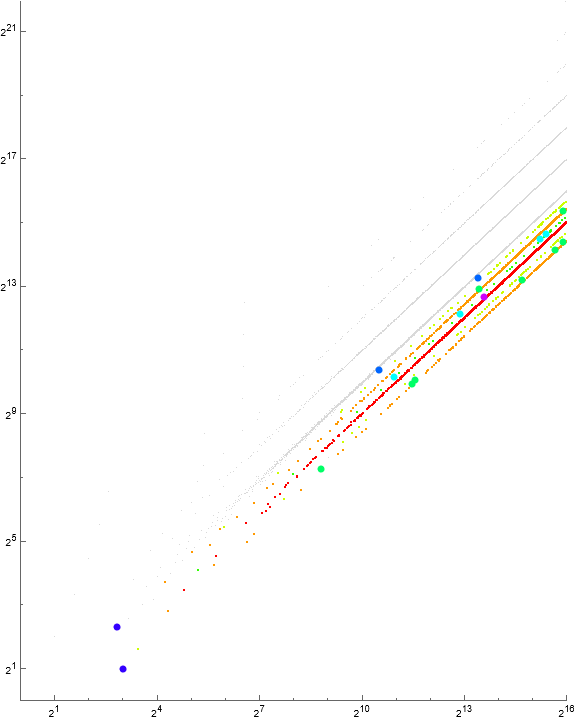
Figure 4.3 is a scatterplot of a(n) for for 1 ≤ n ≤ 216 showing group α in red, group β in blue, and the central group γ in gray.

Figure 4.4 is a scatterplot of a(n) for for 1 ≤ n ≤ 216 showing group α in red, group β in blue, and the central group γ in gray. This figure highlights prime j in yellow and prime k in green. (See Code 10)
Subdivision of group α according to primality of j.
The preponderance of group α associates with prime j. All prime j yield f(j) = 2j in the “prime α” segment for n ≤ 219, and may precipitate the duplation cycle broken only when we obtain composite (k+1).
There are notable terms in the group that do not associate with prime j. The list of these “composite α” indices begins:
102, 1529, 2672, 6471, 7012, 14620, 19828, 22737, 27436, 31841, 37549, 39201, 52841, 59480, 68470, 72272, 72785, 73660, 82180, 83806, 91141, 92327, 92545, 93089, 99147, 102836, 114587, 121800, 125608, 125627, 128790, 131933, 141339, 147265, 152956, 154038, 157036, 158833, 162327, 166032, 169948, 175486, 175559, 191236, 194288, 195936, 206172, 210831, 214806, 220033, 220369, 221505, 224133, 237055, 242837, 248442, 260816, 285111, 288289, 295639, 301316, 312606, 318631, 318930, 322976, 343863, 348200, 357884, 363821, 368362, 374758, 374922, 376187, 383532, 383568, 386596, 389455, 393545, 406541, 417926, 418426, 439185, 445890, 454919, 456617, 459434, 461677, 467973, 469030, 472307, 489462, 490513, 503901, 505157, 518822, 519629, ...
The first case a(102) = 96 exemplifies the “composite α” phenomenon; f(32) = 96, with the lesser or equal powers of the power range of 2 appearing at n in {8, 2, 12, 21, 30, 69}. We have composite j → 3j in all cases listed above. The case a(102) only happens to involve a perfect prime power. Composite α terms are even and belong to 2 (mod 3), hence k = 3j to satisfy the condition k ◊ j. Terms j = a(i−1) + 1 for i listed immediately above begin:
32, 500, 878, 2132, 2312, 4832, 6548, 7508, 9068, 10532, 12422, 12968, 17492, 19688, 22670, 23930, 24098, 24392, 27212, 27752, 30188, 30578, 30650, 30830, 32840, 34058, 37958, 40352, 41612, 41618, 42668, 43712, 46820, 48782, 50672, 51032, 52028, 52628, 53792, 55010, 56312, 58148, 58172, 63368, 64382, 64928, 68330, 69878, 71192, 72932, 73040, 73418, 74288, 78572, 80492, 82352, 86468, 94532, 95582, 98018, 99908, 103652, 105650, 105752, 107090, 114032, 115472, 118688, 120662, 122168, 124298, 124352, 124772, 127208, 127220, 128222, 129170, 130532, 134852, 138638, 138800, 145688, 147920, 150908, 151472, 152408, 153152, 155252, 155600, 156692, 162392, 162740, 167198, 167612, 172148, 172412, ...
We observe for all j listed above, 2 | j.
Therefore, the terms in group α for which C = 3 (j | k, k ◊ j) either have prime j, f(j) = 2j, or composite j, f(j) = 3j, both cases strictly increasing by an integer factor. Hence we may distinguish prime-α from composite-α merely by the coefficient m. This is demonstrated by Figure 3.2, which shows group α in color and all other terms in gray. in Figure 3.2, prime-α appears in blue while composite-α appears in red. Furthermore, the duplation cycle phenomenon concerns consecutive prime-α terms.
Subdivision of group β according to primality of k.
Group β has only a single composite k result: a(33) = 25 for j = 75. For all remaining members of the group, k is prime. It is unclear if there are other composite k in group β for n > 219. Therefore, generally, we have strictly decreasing f(j) → k for composite j leading to prime k | j except in the case of a(33). The terms in this group exhibit “mediation” described in section 3.
Furthermore, throughout group β, ω( j) = 2 but for a(33), Ω( j) = 3 while for all other terms, Ω( j) = 2. Generally in this group we see squarefree semiprime j yield prime k. Though k | j does not necessitate prime k, it seems that such terminates decline. Does this hold for n > 219?
Bisections of central group γ.
The regular relationships C = 5 (j | k ∧ k || j), C = 8 (j || k ∧ k || j), and the rare C = 7 (j || k ∧ k | j) appear in the central group along with the most estranged symmetrically semicoprime C = 0 (j ◊ k ∧ k ◊ j) and the other mixed neutral states C = 2 (j ◊ k ∧ k || j) and C = 6 (j || k ∧ k ◊ j).
Completely Neutral States.
Completely neutral states C in {0, 2, 6, 8} prohibit prime j or k. For C in {0, 2, 6}, we see either j > k or k > j, therefore we call them ambidirectional. We may regard these cases as completely neutral constitutive states (cases that do not involve divisors). States {0, 2, 6} may be even or odd.
Table 4.5 summarizes qualities of completely neutral states.
Down Up Even Odd 2/3* 2/5* Other Total
-----------------------------------------------------------------------------
0 (j ◊ k ∧ k ◊ j) 184115 269453 236174 217394 144 - 453424 453568
2 (j ◊ k ∧ k || j) 160 159 26 293 81 - 238 319
6 (j || k ∧ k ◊ j) 31 215 224 22 - 42 204 246
8 (j || k ∧ k || j) - 14 14 - - 14 - 14
* ratios of increase only. Other ratios are ambidirectional.
State 0 represents the least order in a. Even state 0 terms may pertain to increase (193839 terms) or decrease (42335 terms), as odd pertains to increase (75614) or decrease (141780) as well. All 144 terms featuring j/k = 2/3 are odd and structurally represent increase. The first such term is a(16) = 15, for which j = 10.
Even terms in state 2 concern increase, while odd may pertain to increase (133) or decrease (160). Are there any even terms that concern decrease? All 81 terms featuring j/k = 2/3 are odd and structurally represent increase. The first such term is a(3271) = 3231, for which j = 2154.
Even state 6 terms concern increase (214) or decrease (10), while odd concern increase (1) or decrease (21) as well. All 42 terms featuring j/k = 2/5 are even and structurally represent increase. The first such term is a(703) = 680, for which j = 272.
For C = 8, the symmetrical semidivisor state, j || k ∧ k || j. The relation is completely neutral hence both j and k must be composite. Furthermore, j and k share the same distinct prime divisors; they have the same squarefree kernel. In the 219-term dataset of a, only 14 terms with state 8 exist. These terms are listed in Table 4.4 . Though nothing prevents gcd(j,k) > 2, the 14 terms in state 8 are even, furthermore, all terms have j and k congruent to 0 (mod 10). All exhibit j < k, though there is no prohibition against the contrary. The ratio j/k = 2/5 for all terms of state 8. Do terms with this state exist such that j > k? Short of this, are there mutually semidivisible terms j < k such that j/k = 2/3?
Regarding the first question, suppose we have 2 composite numbers m < n. If ω(n) = 1 and p | n, then there is no m < n such that m || n because gcd(m,n) = p, all n-regular m | n, and the only completely-semidivisible option for such m are perfect powers n = pem. For all other composite m, there is at least one n < m regular to m, however this m has the relation C = 5 (m || n ∧ n | m). Indeed, mutually semidivisible numbers m and n have the same squarefree kernel K, hence the smallest symmetrical semidivisors such that m > n are m = 18, n = 12. Therefore there is latitude to have j > k, however it seems that such k already appears in the sequence by the time it is called for by j.
The second question regards the ratio j/k. The ratio for the 14 terms of state 8 in the dataset is 2/5, a ratio that also pertains to 42 completely neutral and increasing terms with state 6 (j || k ∧ k ◊ j). We would perhaps surmise that the ratio 2/3 might appear for j || k ∧ k || j, j < k; instead, this ratio appears 225 times in the dataset and pertains to symmetrically semicoprime state 0 and state 2 (j ◊ k ∧ k || j). Together, these ratios are fairly rare, while ratios 2/7, 2/11, 2/13, etc. are never seen. Therefore, it seems that the ratio 2/3 forces state 8 to present ratio 2/5, and that nothing forces greater ratios.
States 6 and 8 remain distinct. The former (j || k ∧ k ◊ j) is ambidirectional and appears 246 times in a(n) for 1 ≤ n ≤ 219, only 28 of these instances share ratio 2/5 with completely semidivisible state 8, which appears to be a state of increase.
Completely regular states.
The completely regular states involve j and k that have the same squarefree kernel K. These include C = 5 (j | k ∧ k || j), C = 7 (j || k ∧ k | j), and C = 8 (j || k ∧ k || j). These states are strictly directional, have distinctive parity, and exhibit a consistent ratio j/k. The completely semidivisible state 8 is not structurally restricted to increase and evenness; all the completely regular states certainly could involve multiple ratios. Furthermore, prime j could pertain to state 5 and prime k to state 7, though these are not observed. Instead these seem to be limited only by the mechanics of A347113.
Table 4.6 summarizes qualities of completely regular states.
Down Up Parity Ratio
---------------------------------------------
5 (j | k ∧ k || j) - 1511 Even 1/2
7 (j || k ∧ k | j) 2 - Odd 3
8 (j || k ∧ k || j) - 14 Even 2/5
For C = 5, only j may be prime and therefore structurally, j < k. The bisection γ5 of group γ such that C(n) = 5 includes a(n) with n starting with the following:
2, 12, 21, 216, 397, 579, 889, 1678, 1755, 1916, 2168, 2349, 2896, 2914, 3141, 3254, 3803, 3925, 4051, 4227, 4569, 4652, 5247, 5329, 5406, 5977, 6084, 6111, 6732, 7008, 7255, 7899, 7927, 9006, 9179, 9258, 9372, 9380, 9401, 9902, ...
Only a(2) = 4 has prime j = 2. Therefore, for the bisection γ5, though it is possible to have prime j | k, only the first group γ term has prime j. In all cases, j/k = ½, a ratio shared with C = 3 (j | k ∧ k ◊ j), Perhaps we may see state 5 a special “perchance” completely regular case of state 3, where the fact j | k governs the ratio j/k = ½. The C = 5 bisection represents increase among composites j and k such that j | k and k || j, except for a(2) where j is prime.
For C = 7, only k may be prime, thus structurally, k < j. Bisection γ7 includes a(n) for n in {15, 27} for n < 219. We see a(15) has ( j, k) = (27, 9) and a(27) has (63, 21); both have j > k odd and neither have k prime. The ratio j/k = 3 in both cases, a ratio shared by state 1, hence pertaining to j ◊ k ∧ (k | j ∨ k || j). Because of this, perhaps C = 7 might be regarded as a perchance case of state 1. Are any more terms in this state possible? Are there any terms with prime k?
In general, the nondivisor regular bisections γ5, γ7, and γ8 appear unidirectional; γ5 and γ8 increase and γ7decreases. The semicoprime states that do not involve divisors, γ0, γ2, and γ6, are ambidirectional.
Structural composition of increasing and decreasing j → k.
We may summarise that j < k involves group α (C = 3), but also includes the regular states γ5 and γ8, and an undifferentiated bisection of the semicoprime-semidivisor states γ0, γ2, and γ6.
Setting aside states that do not involve j | k, we see some commonalities:
Table 4.7 summarizes qualities of k-divisor states.
Up 1/2 1/3
---------------------------------------
3 (j | k ∧ k ◊ j) 45544 45448 96
5 (j | k ∧ k || j) 1511 1511 -
Generally, state 3 and 5 enjoy evenness and increase with ratio j/k = ½, in state 3, consistent with prime j and Cunningham chains. Composite-α terms instead feature ratio j/k = 1/3, consistent with composite j, f(j) = 3j. All state-5 terms have composite j except a(2) = 4 for which j = 2.
The decreasing moves j > k involves group β (C = 1), but also includes the regular state γ7 (j || k and k | j), and an undifferentiated bisection of the semicoprime-semidivisor states γ0, γ2, and γ6.
Setting aside states that do not involve k | j, we see some commonalities:
Table 4.8 summarizes qualities of k-divisor states.
Down Parity Ratio
----------------------------------------
1 (j ◊ k ∧ k | j) 23083 Odd* Prime
7 (j || k ∧ k | j) 2 Odd 3
The states 1 and 7 feature odd, decreasing terms with ratios that are prime. State 7 is restricted to ratio 3, while there is a single even term with state 1 (i.e., a(8) = 2, j = 6). All but one state-1 term are prime (the exception being a(33) = 25 for which j = 75), while both state-7 terms are composite. As a consequence of state-1 terms such that a squarefree semiprime j = pq, p < q yields prime k, we have prime ratios j/k. We know, outside of a(7), a(8), and a(11) for which {j, k} = {95, 5}, {6, 2}, and {15, 3}, respectively, k = q, the greatest prime divisor of j, thus, j/k trends small. These prime ratios are listed in Table 4.9 below.
Table 4.9 summarizes prime ratios of a(n) of state 1 along with the number of such pertaining to a(n) for 1 ≤ n ≤ 219.
r. c.
-----------
2 17897
3 4422
5 542
7 158
11 40
13 9
17 4
19 2
23 1
29 3
31 2
37 1
41 1
43 -
47 1
The similarities shared between states 3 and 5, and states 1 and 7, may persuade us to consider these central group γ states γ5, γ7 adjunct to groups α and β, respectively. Therefore we say that we have affinity between α-γ5 which increase and involve ratios 1/2 and 1/3, and same for β-γ7 which decrease, are generally odd, and have prime ratios. There are notable differences, chiefly, the association of group α, i.e., state 3 with records and prime j (outside of the 96 composite-α terms) and the association of group β (state 1) with minima and prime k (outside of a(33) = 25).
Constitutive Signatures of Increase and Decrease.
We may assign a signature based on the concatenation of the C(n) in each increasing or decreasing run. The first such signatures are:
953333, 11, 33, 1, 563, 7, 0, 63, 11, 53, 00, 63, 71, 22, 0, 3, 1, 0, 33, 1, 00, 333, 000, 3, 1, 00, 6, 1, 0, 1, 000, 3, 1, 2, 0, 33, 1, 00, 63, 0, 2, 0, 3, 0000, 3, 000, 3, 1, 000, 6, 0, 2, 0, 333333, 0000, 1, 0, 1, 33, 00, 3, 00, 3, 0000, 3, 11, 000, 6, 0, 33, 00, 633, 00000, 3, 0, 1, 22, 00, 3, 00, 3, 21, 000, 3, 1, 0, 1, 000, 3, 0, 1, 0, 3, 000000, 3, 1, 0000, 6, 0, 1, 0000, 3, 0000, 33, 1, 2, 00, 33, 2, 00, 1, 00, 3, 2, ...
The increasing runs are:
953333, 33, 563, 0, 11, 00, 71, 0, 1, 33, 00, 000, 1, 6, 0, 000, 1, 0, 1, 63, 2, 3, 3, 3, 000, 0, 0, 0000, 0, 33, 3, 3, 3, 000, 0, 00, 00000, 0, 22, 3, 3, 000, 1, 1, 3, 1, 3, 3, 0000, 0, 0000, 0000, 1, 00, 2, 1, 3, ...
The decreasing runs are:
11, 1, 7, 63, 53, 63, 22, 3, 0, 1, 333, 3, 00, 1, 1, 3, 2, 33, 00, 0, 0, 0000, 000, 1, 6, 2, 333333, 1, 1, 00, 00, 0000, 11, 6, 33, 633, 3, 1, 00, 00, 21, 3, 0, 000, 0, 0, 000000, 1, 6, 1, 3, 33, 2, 33, 00, 00, 2, ...
From this we gather the notion that we might classify increasing and decreasing runs according to signatures.
Table A lists 111 distinct increasing-run signatures among 144729 found in the first 219 terms of a(n). The signatures consist of states {0, 2, 3, 5, 6, 8}, with {3, 5, 8} exclusive to increase.
Indeed, we read C = 3 found in 75 of the 117 distinct signatures as tantamount to group α (i.e., state 3) which comprises 45544 of the 316897 terms a(n) with n ≤ 219 such that j < k. Recall that state 3 fosters increase.
We find that many of the 75 signatures that host C = 3 might be divided into a head that does not contain 3, and a tail composed of 3s. These tails are the (prime) duplation cycles, therefore pertain to prime j.
There are 7 signatures that begin with C = 3 (j | k, k ◊ j), 5 of which (“30”, “300”, “3000”, “3003”, “303”) harbor composite-α in the first term, and 2 of which only harbor composite-α given certain circumstances. Signature “3” (a singleton increasing run) for instance, appears 5329 times for n ≤ 219, but only 15 of these signatures harbor composite-α. We recall that the signatures might append context, and find that indeed, of the signature “3”, only those preceded by “01” and followed by “0” (thus “0130”) harbor composite-α. Similarly, 22 of the 874 instances of signature “33”, those preceded by “01” and followed by “0” (thus “01330”) also generate composite-α.
Table B lists 30 distinct increasing-run signatures among 144729 found in the first 219 terms of a(n). The signatures consist of states {0, 1, 2, 6, 7}, with 1 and 7 exclusive to decrease. These signatures are markedly shorter than those of increase.
Group β concerns C = 1 (j ◊ k, k | j), which appears in 12 of the distinct signatures, inhabiting the last term of 11 of these. Only signature “11” has repeated instances of state 1. State 1 appears in 23083 of the 207391 terms a(n) with n ≤ 219 such that j > k. Recall that state 1 must have j > k, therefore foster decrease. State 1 also pertains to prime k for n ≤ 219, however (j ◊ k, k | j) does not forbid composite k. We have not yet seen an instance of composite k.
There are 16 signatures that may denote either increasing or decreasing runs. These are:
0, 00, 000, 0000, 00000, 000000, 002, 02, 020, 06, 2, 20, 6, 60, 600, 6000
These ambidirectional signatures are wholly composed of the symmetrically semicoprime C = 0 (j ◊ k ∧ k ◊ j) and the other mixed neutral states C = 2 (j ◊ k ∧ k || j) and C = 6 (j || k ∧ k ◊ j) that pertain to composite terms. Because of this, we conject that repeated “0”, any signature composed of a number of repeated “0” and terminates in “2”, and any signature that begins with “6” and is followed by repeated “0” are also ambidirectional.
The ambidirectional signatures present challenge to any attempt to generate a by means of constitutive analysis rather than the algorithm on hand.
Constitutive sources of local maxima and minima.
Records in a, outside of the trivial a(1) = 1 and the term a(2) = 4, are the fruit of at least 1 final term generated through certain prime duplation cycles. These are group α terms, that is, terms for which C = 3, i.e., (j | k ∧ k ◊ j). The term a(2) = 4 has relation C = 5 (j | k, k || j), which results from p = 2, f(2) = 2(2) having a different relation than p odd, f(p) = 2p. Clearly, repeated duplation gives the best chance for a(n+1) to set a record in A347113, even if the duplation factor (which certainly is an integer m > 1 via the constraint j | k) isn’t always 2.
Table 6.1. Increasing run signatures that harbor a record (a term in A347307), with i the index of the increasing run signature and a decimal point demarcating record-setting term signatures on the right from non-record setting terms on the left. The figure c is the number of records set in increasing run signature i, and the records are listed at the end of each row.
i Signature c Records
---------------------------------------------------
1 .953333 6 1, 4, 10, 22, 46, 94
8 03.3 1 118
9 003.33 2 166, 334
21 203.33333 5 358, 718, 1438, 2878, 5758
135 0333.3 1 8158
271 02033.3 1 8254
326 0033.33 2 9838, 19678
370 00333.3 1 22558
731 333.3 1 43198
959 0333.3 1 56638
1755 00333.3 1 103198
2886 333.3 1 169438
3151 333.3 1 184798
3250 333.3 1 190558
3306 333.3 1 193918
4689 0333.3 1 274558
5391 333.3 1 315358
5437 00333.3 1 318238
6122 0333.3 1 357598
7198 00333.3 1 419038
7554 00333.3 1 439678
8349 00333.3 1 486238
12035 00333.3 1 698398
14804 333.33 2 858238, 1716478
14857 03333.3 1 1723198
16903 00003333.3 1 1965118
17487 03333.33 2 2029438, 4058878
35240 03333.33 2 4068478, 8136958
74266 3333.3 1 8577598
82052 03333.3 1 9475198
94460 003333.3 1 10909438
112313 3333.33 2 12968638, 25937278
...
A similar table concerning decreasing run signatures could be produced for the 1311 local minima in a(n) for n ≤ 219. The decreasing run lengths are shorter since decrease is hampered by the rarification of available gaps in the range u ≤ k. Only one local minimum is set by any given decreasing run that sets minima. The minimum is set at the end of the decreasing run since immediately after setting a minimum, a(n+1) > a(n); there are no gaps below the least unused u(n).
The trivial minimum, a(1), is found starting the first increasing run and attributes to C = 9, which is merely a special code signifying that a(1) = 1 by definition. All the remaining 1310 minima attribute to C = 1, i.e., (j ◊ k, k | j), which guarantees k < j, therefore, decrease in a as n increases, since j-divisor k must not exceed j. Since all local minima outside of the trivial first one are the result of k | j, all signatures that produce local minima end with state 1. Seven of the 30 decreasing run signatures produce local minima in a(n) for n ≤ 218: {“0001”, “001”, “01”, “1”, “11”, “21”, “71”}. Only “71” “reliably” yields local minima, however, there is only 1 instance of signature “71” in a(n) for n ≤ 219, i.e., a(27..28) = {21,11}: (j,k) = {(63,21), (22,11)}, hence (j || k ∧ k | j) followed by (j ◊ k ∧ k | j). State 7 (j || k ∧ k | j) is the rarest state in in a(n) for n ≤ 219, appearing on only 2 early occasions.
Constitutive nature of fixed points.
Let’s examine the fixed points of a(n) for n ≤ 219, listed in A347314:
1, 24, 66, 70, 88, 156, 180, 476, 480, 484, 1292, 3182, 3440, 3444, 3604, 5724, 6486, 7470, 8466, 12426, ...
It is unclear if there are any others. These terms are even outside of 1, and are terms in increasing runs. Fixed points tend to have the constitutive state 0 outside of the first term (which is 1 by definition), excepting k = 66 for which j = 64. We see 64 || 66 yet 66 ◊ 64, hence state 6. The terms have ratio j/k such that the denominator is 1 more than the numerator.
Bisection of a according to certain constitutive signatures.
We identified certain constitutive signatures that pertain to directionality (increase or decrease) and those that are ambidirectional. Here we are not necessarily concerned with distinguishing increase or decrease, but rather among directionality or ambidirectionality, the latter term signifying signatures that may pertain either to increase or decrease.
In terms of the constitutive function C, increase includes states {0, 2, 3, 5, 6, 8}, with {3, 5, 8} exclusive to increase. In terms of the constitutive function C, decrease includes states {0, 1, 2, 6, 7}, with 1 and 7 exclusive to decrease. This leaves us with states {0, 2, 6} which may pertain to either increase or decrease. We recall that these states are fully neutral with respect to j and k, meaning the terms neither divide nor are coprime to either j or k. Therefore, they pertain only to composite numbers, since primes must either divide or be coprime to another number.
Ambidirectional terms, those that have C in {0, 2, 6}, are composite.
We partition the sequence a according to directionality-ambidirectionality, and derive the sequence as follows where even-indexed terms are ambidirectional and odd-indexed terms are directional:
{1, 4, 10, 22, 46, 94, 5, 2, 6, 14, 3, 8}, {12}, {26, 9}, {15, 18}, {38, 13, 7, 16, 34}, {20, 24, 30}, {62, 21, 11}, ...
Instead of the terms of a, we replace them with the constitutive signatures C and thus produce directional and ambidirectional signatures:
953333113315, 6, 37, 06, 31153, 006, 371, 220, 31, 0, 331, 00, 333, 000, 31, 006, 1, 0, 1, 000, 31, 20, 331, 006, 3, 020, 3, 0000, 3, 000, ...
Table C lists 33 distinct constitutive signatures of directional runs among 59160 seen in a(n) for n ≤ 219.
Among these distinct signatures, we see “15” followed by a number of “3s”, sometimes capped with a final “1”, for instance. This represents a single decline followed by an increasing run, capped at times with a final single-term fall. The most common signatures are the singleton “1” and the singleton “3”. We must remind the reader that it is possible that the adjacent ambidirectional run may sustain an increasing or decreasing run, therefore a singleton “3” may not translate into a complete increasing run (as “3” implies increase on account of j < k).
Since these signatures are directional, we can reliably say that signature “153331” implies a fall, then an increasing run of length 4, then a fall. We do not know whether the first fall is preceded by increase or decrease, and we do not know whether the last fall is followed by increase or decrease.
The first directional signature comprises the first dozen terms of a: “953333113315”. We recall that state 9 is assigned to the first term a(1) as it appears by definition.
The state C = 3 (j | k, k ◊ j), which implies j < k, thus, increase, is found in 31 of the 32 distinct directional signatures; the signatures “1” and “15” do not involve this state.
In this division of a into directional and ambidirectional runs, we find the composite-α instances of state “3” instead in those direction runs “13”, “133”. These signatures harbor a first state “3” involving f( j) = 3j.
The state C = 1 (j ◊ k, k | j), which implies k < j, thus, decrease, is found in 26 of the 32 distinct directional signatures; the signatures that consist of repeated states 3 and “37” do not involve this state. The signatures listed below contain repeated states 1.
311, 31153, 3333311, 953333113315
In contrast to the directional signatures, we have 321 distinct ambidirectional signatures among 19142 seen in a(n) for n ≤219.
Many of the most common ambidirectional signatures are simply repeated states “0”, that is, the symmetric semicoprime case, (j ◊ k ∧ k ◊ j), the case with the least ordering. We find that the other two ambidirectional states,“2” (j ◊ k ∧ k || j) and “6” (j || k ∧ k ◊ j), are quite rare. “6” is always a singleton, and there are instances of repeated “22”, but no further repetitions of the state “2”. There are 436 instances of the signature “26” but none of “62”amid the first 219 terms of a.
The most common and sustained state is that of the symmetric semicoprime case “0”, (j ◊ k, k ◊ j). Table D summarizes findings. In all the repeated state-0 signatures, rise and fall is unpredictable.
Relation of ambidirectional terms with central group γ.
Those terms that fall into ambidirectional signatures are contained within central group γ. This stands to reason, since we have defined group γ essentially as any term in a that does not have states 1 or 3, which imply decrease via k < j or increase via j < k, respectively. Hence we have directional group γ and ambidirectional group γ. The preponderance of group γ is ambidirectional; only 1528 terms in group γ for n < 219 are directional. The indices of the first terms of a that have directional states are:
2, 12, 15, 21, 27, 216, 397, 579, 889, 1127, 1678, 1755, 1916, 2168, 2349, 2896, 2914, 3141, 3254, 3803, 3925, 4051, 4227, 4461, 4569, 4652, 5247, 5329, 5406, 5977, 6084, 6111, ...
It is clear that all a(n) for n in the above sequence are composite, as all central group terms are composite.
Figure 7.1 is a log-log scatterplot of a(n) for 1 ≤ n ≤ 212 showing terms not in the central group γ in blue, ambidirectional terms in central group γ in green, and directional terms in central group γ in red.
Quasilinear features in the scatterplot.
The final investigation we undertake regards the striations in the log-log scatterplot that appear to be evenly separated and parallel.
Alpha striations.
We surmise that the striations in alpha, that is, distinctly above the line a(n) = n in the log-log scatterplot, are echos of central group γ terms brought about through constitutive state 3 duplation. More specifically, we strictly construct the condition to include a(1..2), since these are special cases as already described, but preclude composite-α terms which we know appear amid the central group.
We should thus regard the alpha stripes as 2γ, 4γ, 8γ, 16γ, etc. stripes [5] for those that are respectively the first, second, third, fourth, etc. distinctly above the line a(n) = n.
Therefore we may take the runs of a(1..2) and prime-α terms so as to construct a list of indices of terms in Cunningham chains:
1, 2, 3, 4, 5, 6, 9, 10, 14, 18, 22, 26, 32, 35, 36, 40, 41, 42, 46, 57, 61, 62, 67, 71, 76, 80, 89, 90, 91, 92, 93, 94, 103, 106, 109, 114, 122, 123, 127, 128, 134, 141, 144, 150, ...
Thereafter, we contrive to number the n above instead as (n − i + 1), where i is the index of the most recent initial term of a run of terms in Cunningham chains; for any other n, we set the function to 0 to obtain the mapping upon indices below:
1, 2, 3, 4, 5, 6, 0, 0, 1, 2, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 2, 0, 0, 0, 1, 2, 3, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 2, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, ...
By this, we may obtain the indices L of terms in the various alpha stripes αL = 2Lγ [5].
Indices of the first alpha stripe α1 = 2γ begin:
1, 9, 14, 18, 22, 26, 32, 35, 40, 46, 57, 61, 67, 71, 76, 80, 89, 103, 106, 109, 114, 122, 127, 134, 141, 144, 150, 157, 161, 168, 181, 186, 192, 200, 204, 209, 212, 232, 236, 241, 246, 253, 265, 269, 278, 281, 286, 289, ...
Indices of the alpha stripe α2 = 4γ begin:
2, 10, 36, 41, 62, 90, 123, 128, 187, 193, 242, 254, 266, 290, 312, 424, 439, 463, 500, 517, 602, 655, 670, 675, 687, 765, 776, 823, 927, 976, 1009, 1043, 1072, 1103, 1250, 1260, ...
Indices of the alpha stripe α3 = 8γ begin:
3, 42, 91, 518, 1044, 1251, 1421, 1475, 1507, 1536, 1843, 1922, 1941, 1971, 2747, 3491, 3540, 3590, 3870, 3940, 5145, 5499, 5919, 6166, 6195, 6527, 7224, 7418, 7992, 9054, 9313, ...
It is clear we might go on this way. Hence the striations in the alpha zone where it is clear terms k > n are easily explained. Figure 8.1 plots the alpha striations as identified above.
Figure 8.1 is a log-log scatterplot of a(n) for 1 ≤ n ≤ 216 showing the 2γ striation in red, 4γ in orange, 8γ in gold, 16γ in green, 32γ in blue, and 64γ in purple, accentuating the more rarified striations so as to redner these visible. Central group γ appears immediately below the red 2γ striation, grayed out along with the beta striations below it.
We say these are quasilinear since they reflect the ordering of terms near the central group (which here we lump the composite-α terms along with group γ). The terms in the central group approximate a(n) = n, selecting terms per directive, hence we avoid k coprime to j and k = j. As n increases, the quasilinear features become more refined, as deviation from a(n) = n is increasingly relatively less pronounced.
Beta striations.
We cannot apply the same logic to the beta striations, since the “mediation” cycles (the runs of states 1 or β terms) is never greater than 2 (given 219 terms). Instead, the striations appear as “crashes” from other terms. In examining the indices (n − 1) where a(n) is in state 1, i.e., in group β, we see that the crashes precipitate from terms in the central group.
Let us consider further terms with state 1 (j ◊ k ∧ k | j). These terms have j = pq, p < q, f(pq) = q in cases except the first 3 instances where we have f(pq) = p. The first-mentioned are the greater-prime-β terms, while the lesser-prime-β includes a(7) = 5, a(8) = 2, and a(11) = 3. We know that the ratio j/k for group β terms are prime, and given 219 of the least terms in a, the distinct prime ratios are {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 47}. We know that given 219 of the least terms in a, state 1 is usually found in singleton runs, but sparingly in duplexes.
In fact, the indices of duplexed beta terms with the ratios {3, 2} are:
19, 115, 637, 911, 1030, 2197, 4637, 6891, 7677, 9182, 9254, 12819, 15760, 16887, 19201, 22952, 23279, 24269, 24721, 34009, 37676, 39738, 40535, 40856, 41184, 42904, 43875, 45683, 48586, 49146, 54587, 55723, 56651, 64628, 65801, 68786, 72042, 74997, 78631, 80205, 82491, 83620, 83952, 85728, 91685, 96484, 97376, 100499, 102258, 104905, 106424, 112773, 113472, 120394, 120548, 121066, 123983, 125222, 127975, 129928, 132771, 136008, 137907, 140196, 141741, 145149, 146361, 149301, 152880, 153924, 154502, 156620, 159373, 161155, 162611, 163414, 163818, 166349, 169390, 173823, 174262, 175202, 178396, 179054, 186250, 187075, 197718, 199977, 204584, 205714, 211164, 211814, 211928, 215548, 221107, 221580, 224621, 235647, 236390, 240401, 249850, 254779, 256308, 257110, 259373, 264463, 265786, 266393, 267658, 267675, 271210, 271463, 274005, 277733, 279243, 287874, 288739, 291987, 294880, 301450, 317111, 321013, 321740, 330101, 339618, 341877, 343592, 350369, 350496, 353720, 354960, 356239, 358633, 363107, 365918, 367796, 370761, 371203, 373915, 375205, 375476, 380139, 380282, 381262, 381985, 382153, 384954, 385164, 388456, 401513, 401726, 402001, 407887, 411600, 423451, 423996, 425537, 428940, 434213, 440577, 440792, 444296, 452622, 456768, 466064, 468791, 474017, 476291, 485203, 485407, 490727, 496369, 505230, 509154, 513281, 514042, 517057, ...
There is 1 instance of {19, 3} at a(7) = 5, and 1 instance of {47, 2} at a(144506) = 97777. These constitute all the instances of duplex beta runs. There doesn’t seem to be anything to rule out further duplexes of species other than {2, 3}, and even triplicate, etc. beta runs, though the latter would seem unlikely. The beta runs are of course limited by the rarification of gaps k ≥ u(n) in a(1..n − 1) as n increases, with all 1 ≤ k < u(n) already in a.
An example of a duplexed beta process: a(18) = 38, which becomes j = 39 with gcf(39) = k = a(19) = 13, which in turn becomes j = 14 with gcf(14) = k = a(20) = 7. Thus, we have the succession of ratios {3, 2}. What is necessary is that a squarefree semiprime pq yields q such that q + 1 = p'q', a second squarefree semiprime.
Figure 8.2 demonstrates that beta striations are organized according to prime j/k, but in a way that is non-intuitive. For example, there are two striations that pertain to j/k = 3, spaced a magnitude near 2 apart. a(47) = 29 and a(51) = 19, but both have j/k = 3. For j/k = 5 there appear to be 3 striations, and for j/k = 7, there seem to be at least 2.
We conject (wildly) that there are (q − 1) striations for j/k = q prime, centered about the striation β-2 that pertains to q = 2, but many of these have not yet appeared given 219 terms of a. We put forward this wild conjecture observing the 2 striations pertaining to q = 3, the lower β-32 a bit further from striation β-2 than the higher β-31. For q = 5, we see β-51, β-52, and β-53, but not β-54 (if it exists). Regarding q = 7, perhaps we see β-72 and β-75.
Figure 8.2 is a log-log scatterplot of a(n) for 1 ≤ n ≤ 216 showing beta runs color coded according to the ratio j/k, which is always prime. Red = 2, orange = 3, chartreuse = 5, small green = 7, large green = 11, large cyan = 13, large blue = 17, large indigo = 19, large purple = 29, large magenta = 41.
“Mechanics of the sequence”.
The apparent seeking of the central group for a(n) = k = n is remarkable but unexplained, due to the mechanics of the sequence. The reason why this is remarkable is that numbers k such that gcd( j,k) > 1 presents many terms k < j for highly composite numbers, but for prime j, the least k = 2j; there is nothing structural that prevents, say, 3j, except that 2j is certainly not yet in the sequence and thereby appears after prime j. This is what we mean by “mechanics of the sequence”.
If there is a way to prove that terms k in the central group, meaning any term with states {0, 2, 5, 6, 7, 8} and composite-α, seek to approximate n, then we might also show that indeed, prime j necessitates f( j) = 2j and thus truly, all records pertain to Cunningham chains, the ratio 2/5 pertaining to state 8, the finiteness of terms in state 7, etc.
Conclusion.
Subdivision of A347113.
We can subdivide A347113 into several mutually-exclusive groups of data based on the eight permitted constitutive relations between j and k and primality. State 4 (symmetric divisorship, j | k ∧ k | j) is forbidden, since it implies j = k, which is forbidden by sequence definition. The statistics pertain to a 219 = 524288-term dataset. There are 4 major groups, with central group γ comprising the largest share of terms for n > 16. Primes in the sequence are confined to group β. By far, most of A347113 comprises state 0 (j ◊ k ∧ k ◊ j), the symmetric semicoprime state that is ambidirectional and pertains to j and k both composite.
- a(1) = 1 by definition and pertains to state 9.
- Group α includes all terms in state 3 (j | k ∧ k ◊ j), which implies j < k, therefore generally, k > n. There are 45544 alpha terms.
- Prime-α comprises the lion’s share of this group. We have prime j, thus f( j) = 2j.
- So long as (k+1) is prime, we have a Cunningham chain. Is it possible to have composite j such that f( j) = 2j? Of the 45544 alpha terms, 45448 have prime j, exhibiting ratio j/k = ½.
- Consecutive prime-α terms represents a duplation run (Cunningham chain building).
- All maxima derive from prime-α except a(1) = 1 and a(2) = 4. Therefore, primes j in {2, 5} do not appear in prime-α.
- Composite-α involves even composite j yielding f( j) = 3j, thus f(2m) = 6m and ratio j/k = 1/3. There are 96 such terms. The smallest case is a(102) = 96 from j = 32. These α terms appear among central group γ in scatterplots.
- Prime-α comprises the lion’s share of this group. We have prime j, thus f( j) = 2j.
- Group β includes all terms in state 1 ( j ◊ k ∧ k | j), which implies j > k, therefore generally, k < n. There are 23083 beta terms, all but 1 are prime, and all but 1 (a(8) = 2) are odd.
- Prime-β includes all primes k in a and all local minima aside from a(1). Squarefree semiprime j = pq, p < q, yields f( j) = k prime. The ratio j/k is therefore prime: see Table 4.9 for a breakdown of primes. In this paper we have called this “mediation”.
- Lesser-prime-β includes a(7) = 5, a(8) = 2, and a(11) = 3 for which squarefree semiprime pq yields f(pq) = p. Are there any more terms?
- Greater-prime-β includes 23079 primes a(n), n > 11, for which squarefree semiprime pq yields f(pq) = q. Are all the beta primes a(n), n > 219 in this category?
- Composite-β pertains to the single term a(33) = 25, with j = 75. Are there any others?
- Prime-β includes all primes k in a and all local minima aside from a(1). Squarefree semiprime j = pq, p < q, yields f( j) = k prime. The ratio j/k is therefore prime: see Table 4.9 for a breakdown of primes. In this paper we have called this “mediation”.
- Central group γ includes all remaining 455661 terms; all terms are composite. These terms cluster around a(n) = n in a scatterplot.
- “Divisor-ful”-γ includes 1513 terms m that have an asymmetric divisor relation. For m in this group, gcd( j, k) = min( j, k). Terms in state 5 are even and have j/k = 1/2, a ratio shared with group α.
- γ5 contains 1511 terms that have state 5 (j | k ∧ k || j) that implies j < k.
- Prime-γ5 pertains to the single term a(2) = 4, since j = 2. This is a technicality, since 2 is the least prime p and, via Cunningham chains, 2p || 2. Therefore it could be that a(2) is the only prime of γ5, unless we might have prime j such that f(j) = mj with m = j. It seems highly unlikely, given the size of the dataset.
- Composite-γ5 contains all γ5 terms a(n) for n > 2. The smallest of these 1510 terms is a(12) = 8 for which j = 4.
- γ7 harbors 2 terms with state 7 (j || k ∧ k | j) that implies j > k. These terms are a(15) = 9 for which j = 27, and a(27) = 21 for which j = 63. Both have j > k, are odd, have j/k = 3, and neither have k prime. This is the least common state outside of 9 which only concerns a(1). Are any more terms in this state possible? Are there any terms with prime k?
- γ5 contains 1511 terms that have state 5 (j | k ∧ k || j) that implies j < k.
- Completely neutral γ (or divisor-free γ) includes states that are ambidirectional and restricted to completely composite (j, k).
- γ8 is the symmetrical semidivisor state 8 (j || k ∧ k || j) and includes 14 terms. All terms have j and k congruent to 0 (mod 10), with ratio j/k = 2/5; what would be the reason? All exhibit j < k, though there is no prohibition against the contrary. These terms are listed in Table 4.4 . Do terms with this state exist such that j > k?
- γ2 concerns state 2 (j ◊ k ∧ k || j) and has 319 terms, the least of which is a(29) = 27, with j = 12. These terms occur as singletons or duplexes; duplexes are found in increasing runs; a(28..30) = {11, 27, 32}, which is the least case of duplex. a(145) = 121 has j = 275, a singleton in a decreasing run. Of the 319 terms in this state, 160 are decreasing, 159 increasing, 26 are even and 293 are odd, 81 of the odd have ratio j/k = 2/3, the rest, even or odd, have an assortment of offset ratios. Even terms concern increase, while odd terms are ambidirectional.
- γ6 concerns state 6 (j || k ∧ k ◊ j) and has 246 terms, the least of which is a(13) = 12, with j = 9. Of the 246, 31 represent decline and 215 increase, 224 are even and 22 odd. Even state 6 terms concern increase (214) or decrease (10), while odd concern increase (1) or decrease (21) as well. 42 of the even terms have ratio j/k = 2/5 therefore increase, while the rest, even or odd, have an assortment of offset ratios. This state appears in singleton runs, though there is no prohibition against recurrence. Is there a duplex state 6 in a? Furthermore, we have state 2 followed by state 6 in certain ambidirectional runs, but never 6 followed by 2. Why is this?
- γ0 concerns the symmetrical semicoprime state 0 (j ◊ k ∧ k ◊ j), which represents the least “relatedness” and order in the sequence. State 0 is the most common state in a with 453568 terms; most of A347113 lies in state 0. Of the terms in state 0, 184115 move down and 269453 up; 236174 are even and 217394 odd. Even state 0 terms may pertain to increase (193839 terms) or decrease (42335 terms), as odd pertains to increase (75614) or decrease (141780) as well. All 144 terms featuring j/k = 2/3 are odd and structurally represent increase. There are runs of length 1..82 of terms with state 0 (see Table D)
- Completely regular γ is comprised of γ5, γ7, and γ8, and is directional, with γ5 and γ8 increasing, and γ7 decreasing. (It is possible that γ8 may also decrease.)
- Ambidirectional γ is comprised of γ0, γ2, and γ6, with possible addition of γ8.
- “Divisor-ful”-γ includes 1513 terms m that have an asymmetric divisor relation. For m in this group, gcd( j, k) = min( j, k). Terms in state 5 are even and have j/k = 1/2, a ratio shared with group α.
Following is a recapitulation of interesting facts about A347113. These are simplified in the summary that appeared in the beginning of the paper.
- The sequence scatterplot shows arrangement about a central group (group γ) that approximates a(n) = n. The central group γ contains a(n) such that a(n+1) does not involve j | k or k | j and is the densest part of a for n > 16.
- Group α contains a(n) generally larger than n such that (j | k, k ◊ j), predominated by prime j. Group α has the same number of terms in the interval [2e..2(e+1)) as group γ for e = 3, but by e = 18, the ratio of the number of terms in group γ and in group α is about 10/1. Composite-α terms (those with composite j) appear in the central group.
- Group β contains a(n) generally smaller than n such that (j ◊ k, k | j), harboring prime k in all but one case, a(33) = 25 in a(n) for n ≤ 219. Group α has generally twice the number of terms in the interval [2e..2(e+1)) than those in group β.
- “Towers” appear in the scatterplot, which are Cunningham chains that appear in many increasing runs. These are associated with prime j = p, f(p) = 2p, with the constitutive relation (j | k, k ◊ j). There seems to be a chance that the chains may include poorly divisible composite numbers, however this has not been observed for n ≤219.
- Increase in a represented by j < k involves group α (j | k but k ◊ j, i.e., C = 3), but also includes the regular states γ5 and γ8, and an undifferentiated bisection of the semicoprime-nondivisor states γ0, γ2, and γ6. In terms of the constitutive function C, increase includes states {0, 2, 3, 5, 6, 8}, with {3, 5, 8} exclusive to increase.
- The constitutive signatures of 144729 increasing runs for n ≤ 219 fall into 117 distinct signatures, 75 of which include group α.
- Prime a(n−1)+1 = j is associated with increase in a, since j | k implies j < k because j = k is forbidden by definition of the sequence a. Primes j must either divide or be coprime to k; gcd( j,k) = 1 is forbidden by definition of the sequence a. Hence prime j induces increase and pertains to state 3. Primes predominate group α.
- We can disambiguate prime-α from composite-α through the use of constitutive signatures. Prime-α recurs and comprises the end of certain increasing runs, broken by composite j. Composite-α appears in certain signatures that have the cycle (j ◊ k, k ◊ j) → (j ◊ k, k | j) → (j | k, k ◊ j)* → (j ◊ k, k ◊ j), where the asterisked term appears singly or doubled.
- “Towers” (i.e., Cunningham chains) are instances of repeated state 3 that form the tails of many of the 75 increasing run signatures that contain group α. None of the towers incorporate composite-α, therefore the towers are wholly produced by recurrent mappings f( j) = mj, integer m ≥ 2, (only m = 2 observed) so long as j remains prime.
- Records in A347307 are set at the end of Cunningham chains in all cases except a(1) and a(2). Some increasing runs set multiple records, notably those with indices i in {1, 9, 21, 326, ...}. Increasing run 21 is conspicuous in scatterplots for records set by a(n) for n in {90, 91, 92, 93, 94}.
- Decrease in a represented by j > k involves group β (j ◊ k but k | j, i.e., C = 1), but also includes the regular state γ7 (j || k and k | j), and an undifferentiated bisection of the semicoprime-nondivisor states γ0, γ2, and γ6. In terms of the constitutive function C, decrease includes states {0, 1, 2, 6, 7}, with 1 and 7 exclusive to decrease.
- Prime a(n) = k is associated with decrease in a, since k | j implies j > k because j = k is forbidden by definition of the sequence a. Primes k must either divide or be coprime to j; gcd( j,k) = 1 is forbidden by definition of the sequence a. Hence prime k is the fruit of decrease and pertains to state 1. These primes appear in group β outside of a single composite k: a(33) = 25 for j = 75. (See A347313.)
- The constitutive signatures of 144729 decreasing runs for n ≤ 219 fall into 30 distinct signatures, 12 of which include group β.
- Local minima are set one at a time since k < u and j = k are not allowed by definition of least unused u. Therefore, A347757(k) > A347757(k−1)+1.
- There are ambidirectional constitutive signatures that include the neutral states {0, 2, 6, (8)} and thus concern terms wherein j and k are composite.
Here is a list of the most interesting open questions about A347113:
- Is the sequence a permutation of the positive integers?
- Regarding “towers” and Cunningham chains: it possible to have composite j such that f( j) = 2j? Is it possible that prime j have f( j) = mj for m > 2? It is true that almost all prime j > n, hence 2j would be absent from a(1..n), but we have not proved such.
- Why do composite-α terms, that is, even composite j yielding f( j) = mj, have m = 3?
- We have not proved squarefree semiprime j is the means by which prime k enters the sequence.
- Are there any more lesser-prime-β terms, or is the phenomenon confined to 3 instances?
- Is a(33) = 25, with j = 75, the sole composite-β term?
- Are there any more γ7 terms? Are there any terms with prime k?
- Are there any γ8 terms such that j > k?
- Is there a duplex γ6 term in a?
- Does the constitutive signature “62” appear in a?
- What is the organization of the beta-striations? Are there (r − 1) striations asso ciated with prime ratio r?
This concludes our examination.
Appendix:
References
[1] Michael De Vlieger, The Constitutive Arithmetic Functions, 2019.
[2] Michael De Vlieger, Neutral Numbers, 2011.
[3] Ore 1948, Chapter 4, “Prime Numbers”, page 50, specifically: “Lemma 4-1. A prime p is either relatively prime to a number or divides it” and ensuing proof.
[4] Ronald Graham, Donald Knuth, and Oren Patashnik; Concrete Mathematics: A Foundation for Computer Science, 2nd Ed. (1994) Addison-Wesley Professional, ISBN-13 978-0201558029, see page 115.
“When gcd(m, n) = 1, the integers m and n have no prime factors in common and we say that they’re relatively prime.
This concept is so important in practice, we ought to have a special notation for it; but alas, number theorists haven’t agreed on a very good one yet. Therefore we cry: Hear us, O Mathematicians of the World! Let us not wait any longer! We can make many formulas clearer by adopting a new notation now! Let us agree to write ‘m ⊥ n ’, and to say “m is prime to n,” if m and n are relatively prime.”
[5] N. J. A. Sloane, personal correspondence, 2021 1115-1116. Corrections to the notion of alpha striations with multipliers that are perfect powers of 2 rather than even numbers.
Table A: a lexically sorted list of constitutive signatures for increasing runs. There are 117 distinct increase signatures among 144729 complete signatures found in the first 219 terms of a(n). The column i is the table index, “sig.” = signature, n represents the least index in a that starts an increasing run of signature i, c represents the number of signatures i for a(n) with n ≤ 219 as a measure of the rarity of a given signature, and a(n) is the first term of the first signature i seen in a.
Repeated 3 represents duplation, f(p) = 2p, which sometimes sets records in a. In terms of the constitutive function C, increase includes states {0, 2, 3, 5, 6, 8}, with {3, 5, 8} exclusive to increase. Asterisked signatures containing “3” involve f( j) = 3j.
i sig. n c a(n)
-------------------------------------
1 0 12 39107 52
2 00 19 35474 82
3 000 56 19891 226
4 0000 78 6572 303
5 00000 185 1485 708
6 000000 3447 218 12757
7 0000000 9995 35 36551
8 00000000 31852 3 115700
9 000000003 116033 1 420706
10 00000003 11410 3 41675
11 00000006 46325 1 168246
12 0000003 948 38 3545
13 00000033 120188 1 435813
14 000003 118 278 449
15 0000033 5621 7 20750
16 000006 1214 3 4520
17 00003 41 1423 177
18 000033 179 34 682
19 0000333 21005 7 76531
20 000033333 16903 1 61695
21 00006 40 15 170
22 000063 444 1 1698
23 0003 13 5163 54
24 00033 632 207 2387
25 000333 1667 50 6190
26 0003333 15889 5 58005
27 0006 28 35 117
28 00063 941 5 3518
29 002 49056 1 178214
30 003 10 11213 44
31 0033 111 816 421
32 00333 9 168 38
33 003333 326 24 1247
34 0033333 18406 2 67190
35 006 11 37 48
36 0060 49058 2 178221
37 00603 354 2 1351
38 0063 15 4 64
39 02 16295 1 59456
40 020 588 3 2221
41 0200 85 1 331
42 02006 136 1 521
43 0203 9036 2 33026
44 020333 271 1 1039
45 03 25 12577 105
46 033 8 1395 34
47 0333 520 233 1968
48 03333 135 26 515
49 033333 14857 6 54224
50 0333333 17487 2 63857
51 06 593 20 2246
52 060 62 3 248
53 063 4 9 16
54 0633 30 1 125
55 2 534 40 2016
56 20 514 16 1947
57 200 876 32 3271
58 2000 555 18 2093
59 20000 63290 1 229789
60 20003 80033 2 290331
61 200033333 51464 1 186918
62 2003 1110 12 4138
63 20033 44 1 189
64 203 16 14 69
65 2033 14 2 59
66 20333333 21 1 87
67 22 2230 1 8282
68 22003 32 1 137
69 2203 7 1 29
70 23 68 3 268
71 3 †15 26 5329 109
72 30 * 398 42 1529
73 300 * 16302 8 59480
74 3000 * 19960 1 72785
75 3003 * 10732 2 39201
76 303 * 6170 6 22737
77 33 †22 2 874 9
78 333 512 94 1939
79 3333 731 14 2745
80 33333 14804 2 54013
81 333333 112313 1 407263
82 5 51 165 216
83 50 777 588 2914
84 500 1406 145 5247
85 5000 3745 18 13889
86 50000 127023 1 460466
87 50003 70365 3 255485
88 5003 1131 27 4227
89 50033 44236 1 160643
90 503 233 177 889
91 5033 5837 15 21537
92 50333 92058 1 334107
93 5063 4684 1 17305
94 53 5 315 21
95 533 575 39 2168
96 5333 10096 9 36896
97 53333 20803 2 75831
98 533333 57164 1 207552
99 56 65699 1 238504
100 563 3 1 12
101 6 20 21 85
102 60 204 14 781
103 600 184 11 703
104 6000 207 11 792
105 600003 14045 2 51233
106 6003 1902 2 7060
107 603 274 4 1053
108 63 71 7 277
109 633 19027 1 69397
110 8 293 3 1127
111 80 10775 2 39353
112 800 45338 3 164689
113 8000 30328 2 110105
114 80000 3164 1 11711
115 80003 1197 2 4461
116 8003 48901 1 177668
117 953333 1 1 1
Table B: a lexically sorted list of constitutive signatures for decreasing runs. There are 31 distinct decrease signatures among 144729 found in the first 219 terms of a(n). The column i is the table index, “sig.” = signature, n represents the least index in a that starts a decreasing run of signature i, c represents the number of signatures i for a(n) with n ≤ 219 as a measure of the rarity of a given signature, and a(n) is the first term of the first signature i seen in a. Daggers denote decreasing run signatures that sometimes produce minima, with the number of signatures that generate a minimum. Asterisks denote signatures that (hitherto) have produced minima whenever the signatures occur in a. Minima may not occur adjacently, and associate with the state 1 that terminates the decreasing run.
1 0 5 81017 23
2 00 16 34574 72
3 000 75 5407 291
4 0000 218 617 838
5 00000 4190 37 15544
6 000000 76689 2 278237
7 000001 24147 2 87862
8 00001 6689 35 24587
9 00002 15837 1 57803
10 0001 †5 151 394 581
11 0002 37439 3 135892
12 00021 46475 1 168815
13 001 †70 122 2206 470
14 002 3513 14 13002
15 0021 39936 3 144992
16 01 †204 22 9170 98
17 02 83 62 324
18 020 21983 1 80130
19 021 1391 5 5198
20 06 788 3 2952
21 1 †861 2 10896 11
22 11 †167 1 179 7
23 2 44 50 194
24 20 46 8 201
25 21 †1 33 12 145
26 6 66 12 264
27 60 162 13 619
28 600 285 2 1097
29 6000 59921 1 217564
30 7 3 1 15
31 71 * 6 1 27
Table C: a lexically sorted list of constitutive signatures for directional runs. There are 33 distinct directional signatures among 59160 found in the first 219 terms of a(n). The column i is the table index, “sig.” = signature, n represents the least index in a that starts a directional run of signature i, c represents the number of signatures i for a(n) with n ≤ 219 as a measure of the rarity of a given signature, and k is the index of the list of directional runs that corresponds to the first instance of directional signature i seen in a. Asterisked signatures harbor composite-α, i.e., the first state “3” involving f( j) = 3j.
i sig k c n
--------------------------------------
1 1 9 17285 32
2 13 * 278 72 720
3 133 * 19 21 53
4 1331 47994 1 197541
5 15 45 1143 122
6 153 82 292 201
7 1531 1421 22 4212
8 1533 2128 35 6540
9 15331 385 4 1008
10 15333 5141 7 17279
11 153331 7919 2 27757
12 153333 9926 2 35515
13 1533333 25093 1 97789
14 3 13 32805 40
15 31 5 3303 18
16 311 22 176 59
17 31153 3 1 14
18 318 746 11 2102
19 3181 211 1 533
20 31813 16164 2 60630
21 33 23 2877 61
22 331 6 455 23
23 333 7 534 26
24 3331 347 20 901
25 3333 232 58 587
26 33331 104 11 256
27 33333 7271 10 25263
28 333331 31936 1 127032
29 3333311 17987 1 68184
30 333333 17 4 51
31 37 2 1 13
32 371 4 1 16
33 953333113315 1 1 1
Table D: constitutive signatures of repeated “0”, that is, the symmetric semicoprime case, (j ◊ k, k ◊ j), an ambidirectional signature that represents the least order in a. The first column i represents the number of consecutive states “0”, while k represents the index of the partition of a into contiguous terms with state-0 and those with non-state 0. The column n represents the least index in a where we find a run of states-0 with consecutive length i. The last column c represents the number of instances of states-0 repeated i times in a for n ≤ 219, as a measure of the commonness of the signature.
i k n c
--------------------------
1 1 16 5887
2 2 23 6128
3 6 43 6638
4 14 72 5545
5 27 129 4667
6 36 162 4123
7 124 569 3586
8 57 256 3227
9 93 410 2886
10 249 1226 2337
11 193 929 1992
12 156 733 1782
13 95 425 1486
14 128 587 1251
15 105 475 1166
16 419 2206 994
17 245 1196 799
18 237 1154 710
19 913 5258 591
20 587 3187 511
21 488 2605 456
22 258 1275 382
23 748 4169 363
24 1305 7809 284
25 1451 8843 248
26 1289 7703 202
27 2444 15840 165
28 1743 10878 155
29 1206 7149 138
30 3027 20080 116
31 777 4352 98
32 2229 14331 90
33 1878 11836 66
34 2322 14983 52
35 7539 55390 48
36 8151 60228 47
37 8640 64314 34
38 8085 59686 25
39 4135 28471 29
40 19982 160532 16
41 8861 66184 14
42 11613 88842 15
43 20415 164236 11
44 8559 63662 8
45 4554 31670 13
46 13412 103900 4
47 23171 188406 7
48 3538 23899 9
49 36431 308604 5
50 13353 103361 6
51 24105 196791 8
52 33612 282937 3
53 11602 88708 1
54 35335 298765 3
55 33393 280942 1
56 30622 255496 2
58 25968 213533 2
59 20163 162034 1
60 41828 358646 1
65 54214 474725 2
76 34217 288427 1
82 31461 263226 1
a347113 = Block[{a = {1}, c, k, m, u = 2},
Monitor[Do[Set[k, u]; If[PrimeQ[#], m = 2;
While[IntegerQ[c[m #]], m++]; k = m #,
While[Or[IntegerQ[c[k]], k == #, GCD[k, #] == 1], k++]] &[a[[-1]] + 1];
AppendTo[a, k]; Set[c[k], i];
If[k == u, While[IntegerQ[c[u]], u++]], {i, 2^16}], i]; a]
Code 2: Generate maxima r in A347307 and their indices in a stored in A347308:
Set[{a347307, a347308},
With[{s = Union@ FoldList[Max, a347113]}, {s,
Map[FirstPosition[a347113, #][[1]] &, s]}]
Code 3: Generate least unused u in A347755, local minima s in A347756, and their indices in a stored in A347757:
a347755 = Block[{nn = Length@ a347113, a, u = {1}, v = 1},
a = a347113[[1 ;; nn]];
Monitor[
Do[If[a[[i]] == v, While[! FreeQ[a[[1 ;; i]], v], v++],
AppendTo[u, v]], {i, nn}], i]; u];
a347756 = Union@ a347755
a347757 = Map[FirstPosition[a347113, #][[1]] &, a347756]
Code 4: Generate characteristic functions for prime j (here called q) and prime k (here called p)
a347113p = Map[Boole@ PrimeQ@ # &, a347113] (* k-prime characteristic *);
a347113q = Map[Boole@ PrimeQ@ # &, 1 + a347113] (* j-prime characteristic *);
Code 5: Generate first differences of a, increasing run starts and lengths, decreasing run starts and lengths, and indices of inflexion in a:
a347113d = Differences@ a347113;
Set[{a347113ii, a347113il},
Transpose@ Map[{First[#], Length[#]} &,
SplitBy[Prepend[Range[2, # + 1]*Sign@ a347113d[[1 ;; #]], 1], Sign] &[
Length[a347113] - 1][[1 ;; -1 ;; 2]]]]
(* increasing run starts and length *);
Set[{a347113di, a347113dl},
Transpose@ Map[{First[#], Length[#]} &,
-SplitBy[Prepend[Range[2, # + 1]*Sign@ a347113d[[1 ;; #]], 1], Sign] &[
Length[a347113] - 1][[2 ;; -1 ;; 2]]]]
(* decreasing run starts and length *);
a347113inf = Accumulate[Length /@
SplitBy[Prepend[a347113[[2 ;; # + 1]]*Sign@ a347113d[[1 ;; #]], 1], Sign] &[
Length@ a347113d - 1]] (* inflexions *);
Code 6: Generate constitutive analysis of j → k and k → j, and produce reflexive constitutive state codes for each term:
a347113c = With[{s = Partition[a347113, 2, 1]},
Map[Which[Mod[#2, #1] == 0, 0, PowerMod[#2, #2, #1] == 0, 1, True, -1] & @@
{#1 + 1, #2} & @@ # &, s]] (* constitutive j->k *);
a347113cc = With[{s = Partition[a347113, 2, 1]},
Map[Which[Mod[#1, #2] == 0, 0, PowerMod[#1, #1, #2] == 0, 1, True, -1] & @@
{#1 + 1, #2} & @@ # &, s]] (* constitutive k->j *);
a347113ccc = {9}~Join~Array[3*(1 + a347113c[[#]]) + (1 + a347113cc[[#]]) &,
Length[a347113] - 1] (* reflexive constitutive analysis *);
Code 7: Bisect the sequence into groups alpha, beta, and gamma:
a347113ga = Select[Range@ Length[a347113], a347113ccc[[#]] == 3 &]
(* group \[Alpha] *);
a347113gb = Select[Range@ Length[a347113], a347113ccc[[#]] == 1 &]
(* group \[Beta] *);
a347113gc = Select[Range@ Length[a347113], FreeQ[{1, 3}, a347113ccc[[#]]] &]
(* group \[Gamma] *);
Block[{nn = 2^16, a, b, r, s, u, out = -120},
a = a347113[[1 ;; nn]];
b = Map[#2 - (#1 + 1) & @@ # &,
Partition[a347113[[1 ;; nn + 1]], 2, 1]];
r = Array[If[FreeQ[a347308, #], out, a[[#]]] &, nn];
s = Array[If[FreeQ[a347757, #], out, a[[#]]] &, nn];
u = a347755[[1 ;; nn]];
ListPlot[{u, a, r, s}, ImageSize -> Large,
ScalingFunctions -> {"Log2", "Log2"},
PlotRange -> {{1, nn}, {1, Max[a]}}, AspectRatio -> Full,
Joined -> {True, False, False, False}, Mesh -> Full,
PlotStyle -> {Directive[Hue[1/7], PointSize[Medium]],
Directive[Black, PointSize[Small]],
Directive[Red, PointSize[Medium]],
Directive[Blue, PointSize[Medium]]}]]
Block[{nn = 2^16, a, b, c, c0, c1, c2, c3, c5, c6, c7, c8, q, qq, out = -120},
a = a347113[[1 ;; nn]];
c = {-1}~Join~a347113ccc[[1 ;; nn - 1]];
c0 = Array[If[c[[#]] == 0, a[[#]], out] &, nn];
c1 = Array[If[c[[#]] == 1, a[[#]], out] &, nn];
c2 = Array[If[c[[#]] == 2, a[[#]], out] &, nn];
c3 = Array[If[c[[#]] == 3, a[[#]], out] &, nn];
c5 = Array[If[c[[#]] == 5, a[[#]], out] &, nn];
c6 = Array[If[c[[#]] == 6, a[[#]], out] &, nn];
c7 = Array[If[c[[#]] == 7, a[[#]], out] &, nn];
c8 = Array[If[c[[#]] == 8, a[[#]], out] &, nn];
ListPlot[{c0, c1, c2, c3, c5, c6, c7, c8}, ImageSize -> Large,
ScalingFunctions -> {"Log2", "Log2"},
PlotRange -> {{1, nn}, {1, Max[a]}}, AspectRatio -> Full,
PlotStyle -> {
Directive[Blue, PointSize[Small]],
Directive[Purple, PointSize[Small]],
Directive[Darker[Cyan], PointSize[Medium]],
Directive[Magenta, PointSize[Small]],
Directive[Hue[1/7, 1, .875], PointSize[Large]],
Directive[Cyan, PointSize[Medium]],
Directive[Orange, PointSize[Large]],
Directive[Green, PointSize[Large]]}]]
Block[{nn = 2^16, a, ga, gb, gc, p, pp, q, qq, out = -120},
a = a347113[[1 ;; nn]];
ga = Array[If[FreeQ[a347113ga, #], out, a[[#]]] &, nn];
gb = Array[If[FreeQ[a347113gb, #], out, a[[#]]] &, nn];
gc = Array[If[FreeQ[a347113gc, #], out, a[[#]]] &, nn];
q = {0}~Join~a347113q[[1 ;; nn - 1]];
qq = Array[If[q[[#]] == 1, a[[#]], out] &, nn];
p = a347113p[[1 ;; nn]];
pp = Array[If[p[[#]] == 1, a[[#]], out] &, nn];
ListPlot[{qq, pp, a, ga, gb}, ImageSize -> Large,
ScalingFunctions -> {"Log2", "Log2"},
PlotRange -> {{1, nn}, {1, Max[a]}}, AspectRatio -> Full,
PlotStyle -> {
Directive[Yellow, PointSize[Medium]],
Directive[Green, PointSize[Medium]],
Directive[LightGray, PointSize[Tiny]],
Directive[Red, PointSize[Small]],
Directive[Blue, PointSize[Small]]}]] (* Groups *)
Concerns OEIS sequences:
A000005: The divisor counting function τ(n).
A001055: Number of multiplicative partitions of n.
A347113: a(1) = 1, j = a(n−1)+1, a(n) = least unused k such that ( j,k)≠1, j ≠ k.
A347306: Inverse of A347113.
A347307: Maxima of A347113.
A347308: A347307(n) is found at A347113(a(n)).
A347309: gcd( j, k) as defined in this paper.
A347312: Parity of A347113(n).
A347313: Prime(n) is found at A347313(a(n)). Indices of primes k in group β.
A347314: Fixed points of a(n).
A347755: Least unused number u (or least gap u) in A347113(1..n).
A347756: Local minima of A347113.
A347757: A347756(n) is found at A347113(a(n)).
Outline:
- Introduction
- General properties of A347113.
- Maxima and minima.
- Parity.
- Ratio j/k.
- Towers.
- Prime j as the engine behind tower cycles.
- Composite j as an obstacle to tower cycles.
- Increase and Decrease.
- Duplation phases.
- Mediation phases.
- Inflexion points.
- Group γ and the second term of directional runs.
- Constitutive analysis of {j, k}.
- Divisibility and Directionality.
- Constitutive bisection of a.
- Division of a into 3 groups based on divisibility.
- Subdivision of group α according to primality of j.
- Subdivision of group β according to primality of k.
- Bisections of central group γ.
- Completely neutral states.
- Completely regular states.
- Structural composition of increasing and decreasing j → k.
- Constitutive Signatures of Increase and Decrease.
- Constitutive sources of local maxima and minima.
- Constitutive nature of fixed points.
- Bisection of a according to certain constitutive signatures.
- Relation of ambidirectional terms with central group γ.
- Quasilinear features in the scatterplot.
- Alpha striations.
- Beta striations.
- “Mechanics of the sequence”.
- Conclusion.
- Subdivision of A347113.
- Appendix
- References.
- Tables.
- Code.
- Concerns OEIS Sequences.
Document Revision Record.
2021 0903 2200 Draft.
2021 0914 2200 Publication.
2021 0927 1600 Expanded observation based on 524288 terms.
2021 1116 2100 Some corrections and notes attributable to NJA Sloane.