Cardinality of Cardinalities Sequence.

A sequence by David J. Sycamore of Mevagissey, England, UK.
(Originally designated S20220113)
written by Michael De Vlieger 15 January 2022.

Introduction.

Consider a conditional self-referential sequence a that counts the number of appearances of m > 0 in a(1..n). Sycamore’s definition appears below:

a(1)=1. Thereafter, if a(n) is a term that has appeared exactly k times prior to and including itself then a(n+1) is the number of terms prior to and including a(n) which have appeared exactly k times.

Let c(m) represent the cardinality k of m in a(1..n) and q(k) the cardinality of c(m) = k. Therefore the sequence may be defined alternatively as follows:

a(1) = 1; a(n) = q(c(a(n))) × c(a(n)).

The sequence a begins as follows:

1, 1, 2, 1, 3, 2, 5, 2, 6, 3, 8, 3, 9, 4, 5, 11, 5, 12, 6, 14, 6, 15, 7, 8, 17, 8, 18, 9, 20, 9, 21, 10, 11, 23, 11, 24, 12, 26, 12, 27, 13, 14, 29, 14, 30, 15, 32, 15, 33, 16, 17, 35, 17, 36, 18, 38, 18, 39, 19, 20, 41, 20, 42, 21, 44, 21, 45, 22, 23, 47, 23, 48, 24, 50, 24, 51, 25, 26, 53, 26, 54, 27, 56, 27, 57, 28, 29, 59, 29, 60, 30, 62, 30, 63, 31, 32, 65, 32, 66, 33, 68, 33, 69, 34, 35, 71, 35, 72, 36, 74, 36, 75, 37, 38, 77, 38, 78, 39, 80, 39, ...

As a sequence of cardinalities, we can produce 2²⁴ terms using Code 1 in 2 minutes and it is about as easy to generate the terms as it is to store them.

Figure 1.1: Log-log scatterplot of a(n), 1 ≤ n ≤ 2¹⁰, annotating records in red, the first occasion of m highlighted in green, the last occasion of m annotated in blue. The first 64 terms are annotated in black if not already in other categories, and joined by a gray line. Click here for an enlarged plot of 2¹² terms.

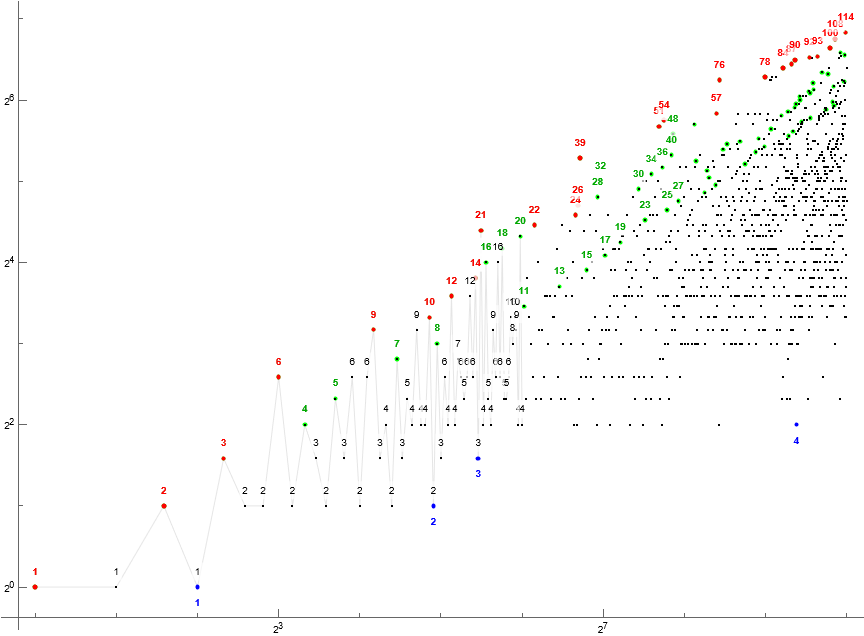
The sequence presents a definite first appearance F(m) of a given term m, where some locally low F(m) set records r in a. It appears that certain largely even numbers first appear early, while largely odd numbers m first appear late. There appear to be trajectories of these late first appearances that conflate with a trajectory of second appearances of some numbers. Most strikingly, there appears to be a last appearance L(m) for m, meaning that there is a finite total number t(m) of appearances of m in a.

What would be the circumstance of a final appearance of m?

Figure 1.2: Scatterplot of a(n), 1 ≤ n ≤ 2²⁰. Click here for an enlarged plot.

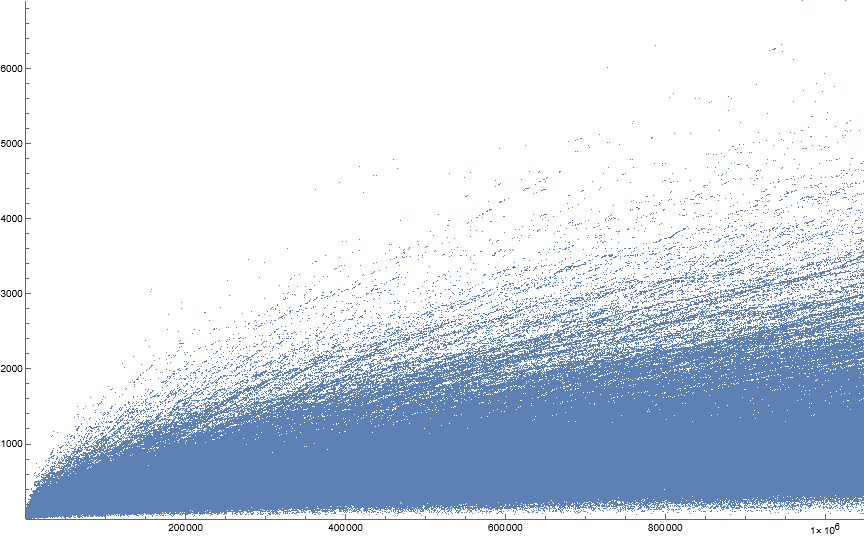
In aggregate the sequence has the appearance of a particularly hairy comet. What is the cause of the filaments in the scalar scatterplot of Figure 1.2?

Auxiliary sequences.

We can track C(n), meaning the value of c(k) for k = a(n−1). This sequence begins as follows:

1, 2, 1, 3, 1, 2, 3, 1, 4, 1, 2, 5, 1, 3, 2, 6, 3, 1, 4, 2, 7, 1, 5, 2, 3, 2, 4, 5, 1, 8, 1, 6, 4, 6, 1, 7, 2, 5, 3, 6, 2, 7, 1, 7, 1, 8, 1, 4, 9, 3, 8, 2, 9, 1, 5, 6, 10, 2, 2, 3, 4, 10, 1, 11, 1, 7, 2, 4, 3, 11, 1, 8, 3, 5, 9, 6, 12, 3, 4, 4, 5, 10, 5, 6, 6, 2, 13, 1, 11, 2, 5, 12, 7, 3, 7, 2, 6, 8, 4, 12, 1, 13, 1, 13, 1, 14, 4, 7, 3, 15, 1, 3, 8, 2, 16, 5, 14, 5, 7, 4, ...

Likewise, we can track Q(n), meaning the value of q(m) at n. This sequence begins as follows:

1, 1, 1, 1, 2, 1, 2, 2, 1, 3, 1, 1, 3, 2, 1, 1, 3, 3, 1, 1, 1, 3, 1, 2, 3, 2, 1, 2, 2, 1, 3, 1, 1, 2, 4, 1, 3, 1, 2, 2, 3, 2, 3, 3, 4, 2, 5, 1, 1, 2, 2, 3, 2, 5, 1, 1, 1, 4, 5, 3, 1, 2, 4, 1, 5, 2, 5, 2, 2, 2, 5, 2, 3, 1, 1, 1, 1, 4, 2, 3, 1, 1, 2, 2, 3, 3, 1, 5, 2, 4, 1, 1, 2, 3, 3, 4, 2, 2, 1, 2, 4, 2, 5, 3, 6, 1, 2, 3, 2, 1, 7, 3, 3, 3, 1, 1, 1, 2, 3, 1, ...

These sequences C and Q are “snapshots” of the cardinalities seen at n, without regard to the numbers to which they pertain. These inputs can be rebuilt, but C and Q are useful as analytical insights. With these, we may produce a table as follows:

n  a(n) c(k) q(m)
------------------
1
2    1    2    1
3    2    1    1
4    1    3    1
5    3    1    2
6    2    2    1
7    2    3    2
8    6    1    2
9    2    4    1
10    4    1    3
11    3    2    1
12    2    5    1
13    5    1    3
14    3    3    2
15    6    2    1
16    2    6    1
17    6    3    3
18    9    1    3
19    3    4    1
20    4    2    1
21    2    7    1
22    7    1    3
23    3    5    1
24    5    2    2
...

This table shows that a(n+1) = c(k) × q(m), where m = c(k), hence c(k) × q(c(k)). For example, for n = 12, we have k = 2, c(k) = m = 5, and q(m) = 1, furnishing m × q(m) = 5 × q(5) = 5 × 1 = 5, thus, a(13) = 5. This means that, given input of 2, we see that there are 5 instances of 2 in a(1..12), and since we have found m = 5 instances, we see that the number of cardinalities 5 in the sequence at n is just 1; only k = 2 appears 5 times. Therefore we multiply the cardinality times the number of cardinalities that have the same value as the currently-reported cardinality to furnish the next term.

Records r appear as follows in a list of such amid the first 2²⁴ terms:

1, 2, 3, 6, 9, 10, 12, 14, 21, 22, 24, 26, 39, 51, 54, 57, 76, 78, 84, 87, 90, 92, 93, 100, 108, 114, 152, 166, 168, 210, 212, 264, 308, 309, 324, 327, 396, 405, 408, 440, 460, 464, 580, 605, 615, 741, 780, 783, 804, 810, 819, 860, 872, 880, 1100, 1105, 1170, 1345, 1386, 1500, 1616, 1625, 1626, 1765, 2073, 2168, 2370, 3033, 3054, 3180, 3456, 3600, 4386, 4484, 4689, 4692, 4788, 4926, 4977, 5022, 5040, 5049, 5070, 5120, 6006, 6304, 6315, 6896, 7056, 7476, 8202, 8244, 8365, 8924, 9416, 10576, 10866, 11780, 13468, 13480, 16176, 16179, 17405, 18822, 20200, 20204, 20308, 20808, 21387, 22785, 22985, 22990, 23504, 23508, 25017, 25023, 26328, 27936, 27978, 28119, 31704, 32263, ...

These appear at the following indices s:

1, 3, 5, 8, 18, 29, 35, 43, 45, 71, 101, 103, 105, 206, 215, 336, 345, 509, 594, 639, 658, 745, 798, 888, 928, 1015, 1042, 1819, 1909, 2460, 2811, 3648, 5131, 5777, 6100, 6122, 7008, 7084, 7181, 10789, 11084, 11126, 11141, 11618, 12698, 14097, 24373, 24468, 28858, 29986, 30820, 31518, 32286, 32779, 32803, 33219, 34928, 60783, 65303, 65432, 81540, 97245, 97656, 103161, 120802, 135353, 150132, 156756, 158131, 252156, 279001, 327252, 362449, 392397, 417377, 417615, 459961, 593227, 625549, 679232, 688063, 689906, 694582, 718181, 727328, 787377, 945337, 971491, 1209277, 1323989, 1339240, 1486205, 1554522, 1655522, 1795463, 1824567, 2315770, 2379077, 2624779, 2733297, 2733382, 3619347, 4740236, 4871555, 6806252, 6807437, 6947660, 6948568, 7450597, 7451097, 9035971, 9038862, 9077900, 9079972, 9217108, 9222487, 9473555, 11861424, 11907983, 12078446, 13624532, 16283858, ...

Records r are those x that appear before all r' < x' < x, that is ahead of numbers since the last record.

Let F(x) be the sequence of indices of the first appearance of x.

1, 3, 5, 10, 13, 8, 22, 31, 18, 29, 65, 35, 88, 43, 111, 47, 130, 54, 148, 63, 45, 71, 183, 101, 221, 103, 243, 122, 304, 173, 334, 125, 316, 193, 311, 212, 429, 283, 105, 229, 470, 356, 507, 369, 412, 482, 624, 232, 648, 537, 206, 279, 696, 215, 751, 586, 336, 620, 858, 656, 917, 663, 908, 687, 1051, 685, 1132, 749, 739, 771, 1261, 915, 1287, 767, 999, 345, 1477, 509, 1558, 873, 828, 1172, 1660, 594, 1358, 1289, 639, 1658, 2053, 658, 2117, 745, 798, 1005, 2247, 970, 2294, 1083, 1146, 888, 2433, 1122, 2465, 2007, 1614, 2261, 2554, 928, 2578, 2627, 1452, 1860, 2793, 1015, 2859, 2874, 1074, 1727, 2235, 1778, ...

Of course s represents the local minima of F.

More interesting is L(x), the last (observed) position of x in a:

4, 30, 44, 666, 2032, 5760, 621, 924, 15696, 24259, 3232, 11255, 3915, 22591, 48181, 25050, 25556, 33223, 56617, 24361, 70993, 61021, 15177, 56025, 67729, 66042, 30244, 129147, 8484, 49271, 10493, 159180, 81961, 74629, 210411, 183709, 15298, 56625, 118265, 169266, 165053, 72007, 464927, 195096, 211632, 139386, 158425, ...

This opens up the question of extinction of x after its last appearance at a(L(x)). For example, it appears that x = 1 appears for the last time at a(4), x = 2 appears last at a(30), and a(44) = 3 is the last time we see x = 3. Those numbers M with particular “longevity”, that is, L(x) sets a record above, include the following:

1, 2, 3, 4, 5, 6, 9, 10, 15, 19, 21, 28, 32, 35, 43, 49, 53, 58, 71, 77, 98, 99, 114, 115, 135, 154, ...

Let t(x) be the total number of times x appears in a:

3, 8, 7, 20, 27, 30, 7, 38, 37, 54, 27, 104, 31, 59, 67, 91, 29, 132, 48, 128, 76, 94, 42, 208, 57, 80, 108, 137, 29, 269, 8, 221, 104, 134, 149, 309, 52, 65, 122, 287, 62, 246, 68, 207, 276, 128, 65, 406, 109, 244, ...

If these numbers represent true totals, then the numbers that appear especially often seem to tend toward numbers that are multiples of 6, at least at small scale. We are not sure of x beyond which t(x) is not reliable, but it seems safe to presume the first dozen or so terms represent true totals.

1, 2, 4, 5, 6, 8, 10, 12, 18, 24, 30, 36, 48, 60, 72, 84, 90, 96, 120, ...

A great amount of terms can be generated, but a proof is required to show that indeed, the number of times t(x) that x appears is indeed finite, and that the last appearance is L(x).

Aggregate behavior of C and Q.

It is easy to see that c(x) is nondecreasing as n increases, since c(x) increments upon the appearance of x as n increases.

*** Work in progress ***

Figure 1.3: Log-log scatterplot of a(n), 1 ≤ n ≤ 2¹², using a color code to indicate the value c(m) = k where red indicates k = 1, and magenta the highest k. Click here for an enlarged plot.

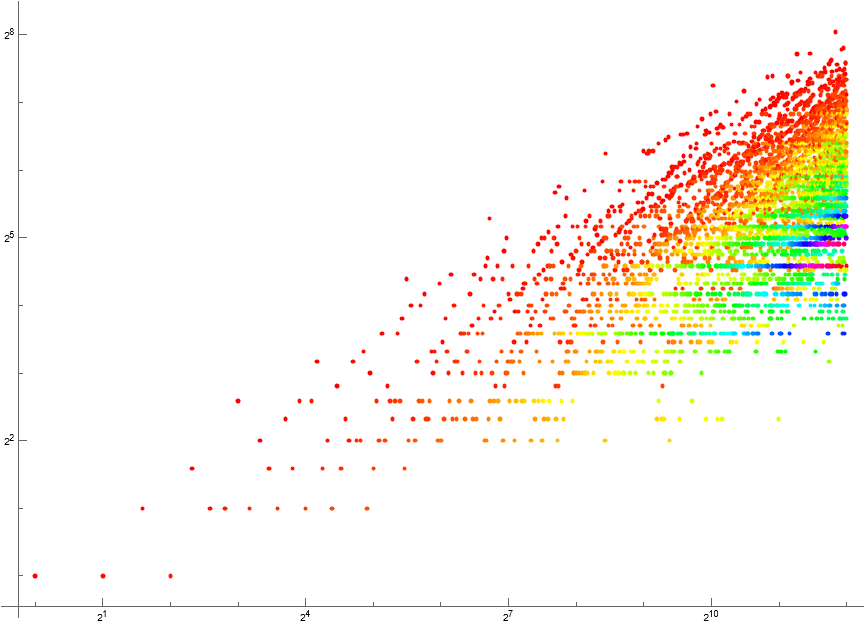
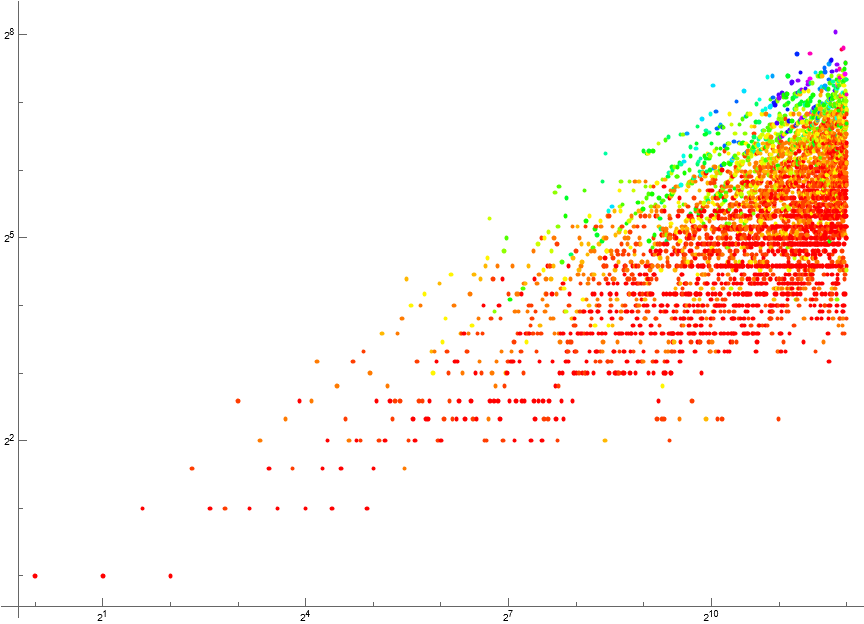
Figure 1.4: Log-log scatterplot of a(n), 1 ≤ n ≤ 2¹², using a color code to indicate the value q(k) = w where red indicates w = 1, and magenta the highest w. Click here for an enlarged plot.

***Work in progress ***

Figure 1.5: Log-log scatterplot of a(n), 1 ≤ n ≤ 2¹², annotating records in red, the last occasions of m in blue. We color code the first appearance of m in gold, second in green, and third in cyan. Click here for an enlarged plot.

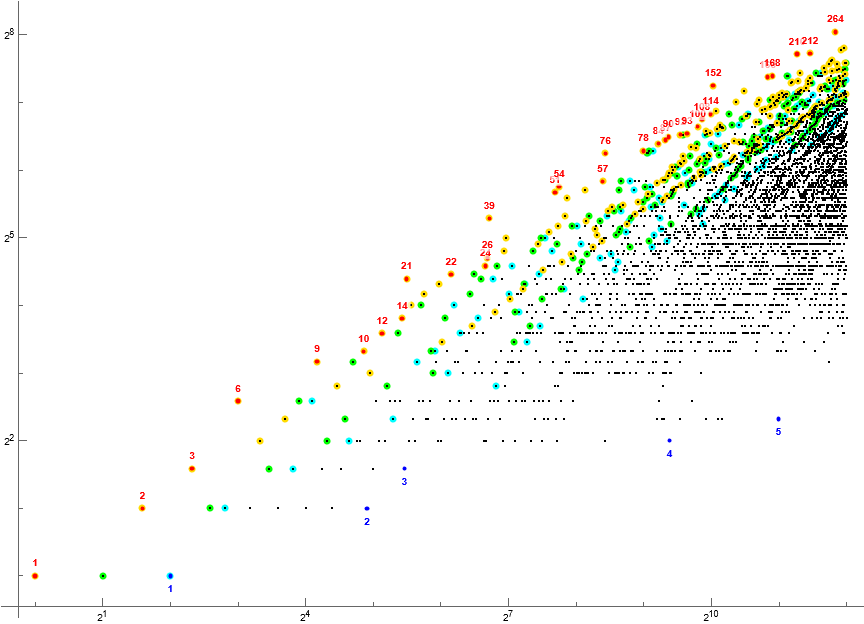
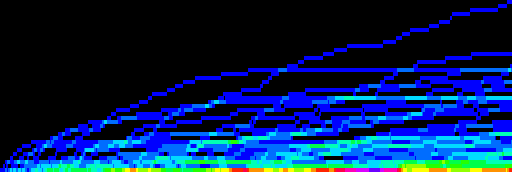
Figure 1.6: Plot of q_n(k), 1 ≤ n ≤ 2⁸, color coded such that black represents w = 0, blue for w = 1, through cyan, green, yellow, orange, red, magenta, and violet as the highest w. Vertical exaggeration 2×. Click here for an enlarged plot of 2¹³ terms with same color scheme, but no vertical exaggeration.

Variant sensitive to appearance rather than quantity.

Let T(1) = 1, and, if T(n) appears more than once in the sequence T, then T(n+1) is the number of terms in the sequence T that have appeared once, else T(n+1) is the number of terms that have appeared more than once. This sequence, S20201216, was studied in depth in another paper.

This sequence T begins as follows:

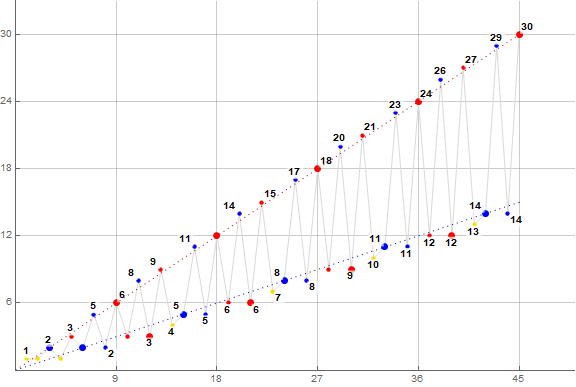
The sequence manifests bifurcation into two trajectories, evident in scatterplot shown by Figure 1.1.

Figure 1.1 is a plot of (n, s(n)) for 1 ≤ n ≤ 45 color coded to show m ≡ 0 (mod 3) in large red, m ≡ 1 (mod 3) in medium gold, and n ≡ 2 (mod 3) in medium blue dots, joining the dots. Aside from m = 1, m ≡ 1 (mod 3) (which appear in medium gold) show only once in the sequence; the red and blue terms m appear thrice each.

Constructing the sequence from counting functions.

Let K represent the set of numbers m that appear just once in the sequence, instantiated at index n and let P represent the multiset of numbers m that have appeared more than once in the sequence, counting multiplicity. We may produce two counting functions κ(n) and π(n), the first counting terms that appear once (κάποτε) in the sequence, instantiated at index n, and the second (πολλοί) counting terms that have appeared more than once (the cardinality of the multiset of m appearing in n with multiplicity). Therefore, κ(n) = cardinality of the set K, and π(n) = cardinality of the multiset P.

We may define sequence s thus:

s(1) = 1, thereafter,
if s(n) appears once in s,
then s(n + 1) = κ(n),
else s(n + 1) = π(n).

(Formula 1)

Conditional congruence relation for n > 5.

One thing to note is the occasion of numbers s(k) = 2k/3 for k ≡ 0 (mod 9). These terms are found in the upper (red) ray and define a line from origin of slope 2/3. Similarly, we find s(k) = k/3 for k ≡ 6 (mod 9), terms found in the lower (blue) ray. These hint at a congruence relation that we might use to describe the rays. Indeed we can write a conditional formula that produces the sequence for n > 5:

Formula 2:

s = {1, 1, 2, 1, 3} for 1 ≤ n ≤ 5;

For n > 5, if n mod 9 ∈ {0, 2, 4, 7}
then s(n) = 2n/3 + (n mod 3)/3
else s(n) = n/3 − (n mod 3)/3 − [n ≡ 3 (mod 9)]
(Iverson brackets)

Clearly, outside of the first five terms (i.e., a(n)), we may calculate s(n) using the conditional congruence relation in Formula 1.

This concludes our examination.

Appendix:

Code 1: Generate a(n); yields 2²⁰ terms in 10 s:

a350768 = Block[{j = 1, k, c, q, m},
  c[_] = q[_] = 0; c[j] = 1;
  {j}~Join~Reap[Monitor[Do[
    Set[k, c[j]]; q[k]++; q[k - 1]--;
    k = k*q[k]; Sow[k]; c[k]++; j = k, {i, 2, 2^20}], i]][[-1, -1]]]

Code 2: Generate s(n) via formula 2 (much faster):

s = {1, 1, 2, 1, 3}~Join~Array[
  If[FreeQ[{0, 2, 4, 7}, #3],
    (#1/3) - #2/3 - Boole[#3 == 3],
    2 (#1/3) + #2/3
  ] & @@ {#, Mod[#, 3], Mod[#, 9]} &, 10^6, 6]

Code 3: Generate s(n) but report κ(n) at points when it changes:

Block[{a = {1}, k = {0}, kk = {}, kw = {0}, p = {0}, pp = {0}, pw = {0}},
  Do[If[Count[a, a[[-1]] ] == 1,
    (AppendTo[a, Total@ #[[All, -1]]];
    AppendTo[k, Total@ #[[All, -1]]];
    AppendTo[kk, i];
    AppendTo[kw,
      StringJoin@
        Riffle[Map[ToString, Union@ #[[All, 1]]], "."]]) &@
        Select[#, Last[#] == 1 &],
    (AppendTo[a, Total@ #[[All, -1]]];
    AppendTo[p, Total@ #[[All, -1]]];
    AppendTo[pp, i];
    AppendTo[pw,
      StringJoin@
        Riffle[Map[ToString,
        Sort@ Flatten[ConstantArray[#1, #2] & @@ # & /@ #]],
          "."]]) &@ Select[#, Last[#] > 1 &]
    ] &@ Tally[a], {i, 60}];
  Array[{kk[[#]] - 1, Mod[kk[[#]] - 1, 9], k[[#]], kw[[#]]} &,
    Length@ k - 1]] // TableForm

Code 4: Generate s(n) but report π(n) at points when it changes:

Block[{a = {1}, k = {0}, kk = {}, kw = {0}, p = {0}, pp = {0}, pw = {0}},
  Do[If[Count[a, a[[-1]] ] == 1,
    (AppendTo[a, Total@ #[[All, -1]]];
    AppendTo[k, Total@ #[[All, -1]]];
    AppendTo[kk, i];
    AppendTo[kw,
      StringJoin@
        Riffle[Map[ToString, Union@ #[[All, 1]]], "."]]) &@
        Select[#, Last[#] == 1 &],
    (AppendTo[a, Total@ #[[All, -1]]];
    AppendTo[p, Total@ #[[All, -1]]];
    AppendTo[pp, i];
    AppendTo[pw,
      StringJoin@
        Riffle[Map[ToString,
        Sort@ Flatten[ConstantArray[#1, #2] & @@ # & /@ #]],
          "."]]) &@ Select[#, Last[#] > 1 &]
    ] &@ Tally[a], {i, 60}];
  Array[{pp[[#]] - 1, Mod[pp[[#]] - 1, 9], p[[#]], pw[[#]]} &,
    Length@ p - 1]] // TableForm

Document Revision Record.

2022 0114 2230 Created.
2022 0119 2200 Draft.