A self-referential internal divisor-sum sequence.
A sequence of David Sycamore.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0318.
Introduction.
We examine a self-referential sequence a that employs an internal divisor sum function, defined as follows:
a(1) = 1; a(n+1) = Σ_{d | a(n)} d cd, where cd is the number of instances of d | a(k) for 1 ≤ k < n.
The sequence a begins:
1, 1, 2, 5, 9, 17, 23, 30, 89, 98, 184, 399, 664, 1292, 2587, 2814, 6619, 6636, 18120, 54896, 110193, 153492, 358310, 645055, 774115, 928993, 1054187, 1116276, 3029874, 6151929, 9505403, 9635864, 20648677, 23744657, 23744691, 35510476, 63144245, 76468986, 182228133, ...
a(2) = 1 since we have 1 instance of 1 | a(k) for 1 ≤ k < n (which we shall abbreviate hereinafter as a count 1(1)).
a(3) = 2 since 2(1) = 2.
a(4) = 5 since 3(1) + 1(2) = 5.
a(5) = 9 since 4(1) + 1(5) = 9.
a(6) = 17 since 5(1) + 1(3) + 1(9) = 17.
a(7) = 23 since 6(1) + 1(17) = 23.
etc.
This sequence can be generated by Code 1; the numbers m become fairly large and the determination of the divisors of m begin to require quite some time to generate as we move past n = 300. We have generated 321 terms.
Let m = a(n), the progenitor of a(n + 1).
The sequence accelerates when m is highly divisible, and stalls when m is prime. In any case, the sequence strictly increases, since 1 | m for all m. Therefore a(n + 1) ≥ n + m for n > 3. We see that for m = p prime, a(n + 1) = n + m = n + p.
Furthermore it seems that smaller d might accrue instances in a granular way at the beginning of the sequence, but given enough iterations of the function, we might see a distribution that favors smaller highly divisible d over large prime d. This situation is likely akin to what is seen at the divisor-counting version of this sequence, A342616.
Figure 1 is an annotated log-log scatterplot of a(n) for 1 ≤ n ≤ 24. We color a(n+1) red if a(n) is prime.
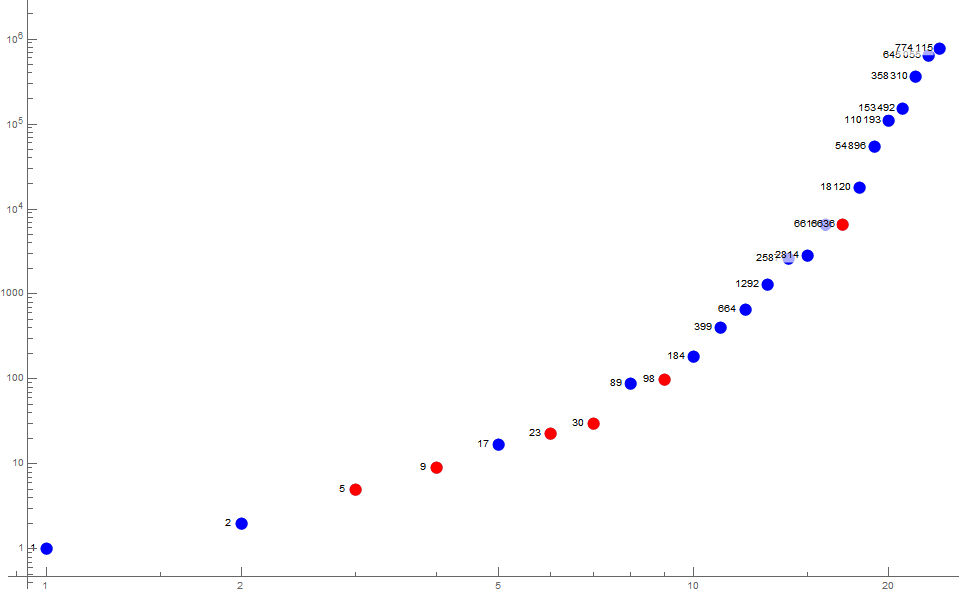
Figure 1 illustrates the acceleration of the sequence given highly divisible m, and its retirement to a(n+1) = n + a(n).
Primes rarely appear in the sequence. For 1 ≤ n ≤ 321, we have the following primes:
2, 5, 17, 23, 89, 6619, 23744657, 922682749, 70964542696933, 11282319824706191924527, 2033275159493211496365849751
The paucity of primes in the sequence is likely due to their increasing rarity as m increases. It seems unlikely that there would be a point after which all terms in a are composite, mainly on account of the additive nature of Σ_{d | a(n)} d cd.
Figure 2 is an annotated log-log scatterplot of a(n) for 1 ≤ n ≤ 321. We color a(n+1) red if a(n) is prime.
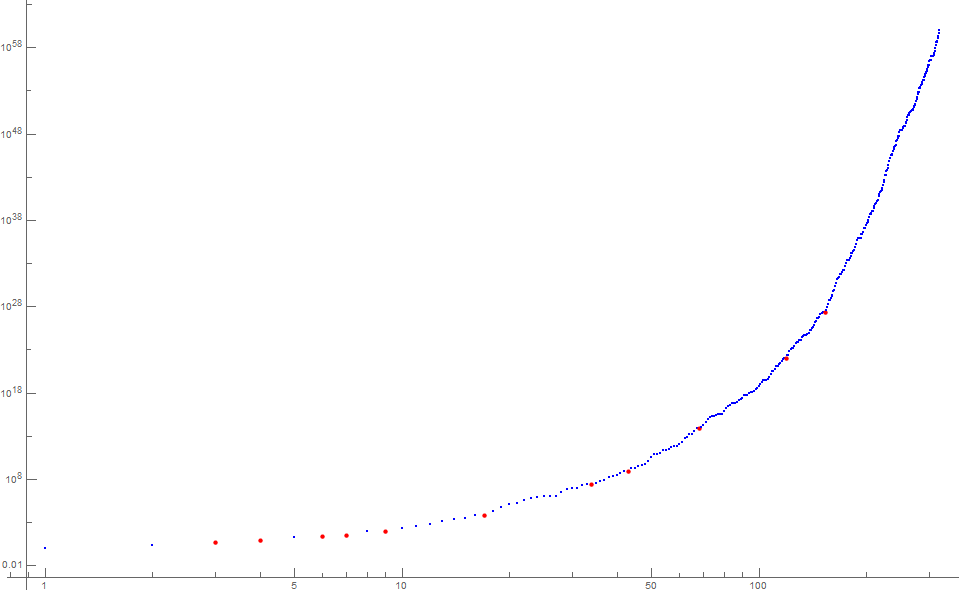
Consider the divisor sum function σ(n). We observe that a(n+1) ≥ σ(m), remaining close to σ(m).
Figure 3 is an annotated log-log scatterplot of a(n) for 1 ≤ n ≤ 64. We use a color function to indicate the number of divisors τ(m) for m = a(n − 1).
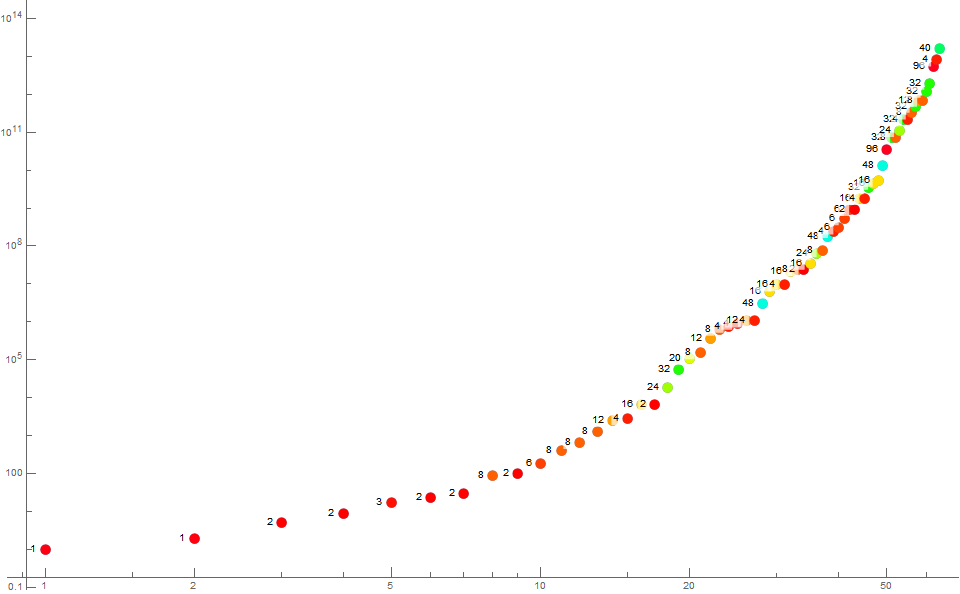
Figure 4 is an annotated log-log scatterplot of a(n) for 1 ≤ n ≤ 64. We use a color function to indicate the index i of the least number b of same prime signature as m = a(n − 1) as a means to understand the prime decomposition of m.
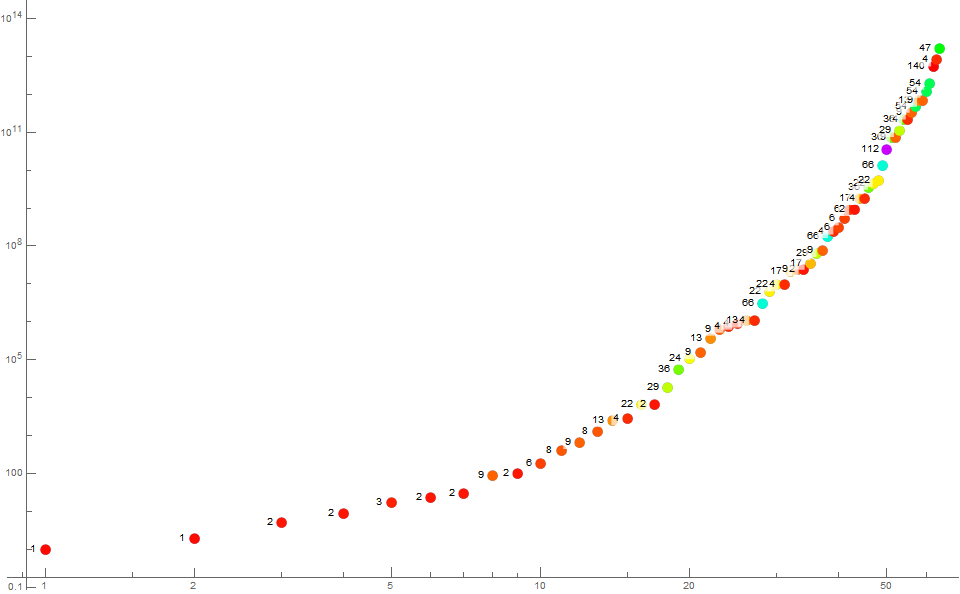
Figure 5 is a list of primitive prime signatures A025487(i) found in the first 321 terms of a. The dot diagrams function as a histogram of multiplicities of primes, sorted greatest to least. The bold numbers are the indices i and the italic numbers are A025487(i).

This concludes our examination.
Appendix:
Table A lists the first 100 terms of sequence a. The column asterisked places "1" for the empty product, "p" for prime a(n), and "*" for squarefree semiprimes. Column i is the index in A025487 that corresponds to the prime decomposition of a(n), and the column following that is A025487(i), the smallest number that has the same prime signature as a(n). The last column attempts to succinctly compactify the prime power decomposition of a(n) via row a(n) of A287352 (π-code).
n a(n) * i A25487(i) A287352(a(n))
------------------------------------------------------------
1 1 1 1 1 0
2 2 p 2 2 1
3 5 p 2 2 3
4 9 3 4 2.0
5 17 p 2 2 7
6 23 p 2 2 9
7 30 * 9 30 1.1.1
8 89 p 2 2 24
9 98 6 12 1.3.0
10 184 8 24 1.0.0.8
11 399 * 9 30 2.2.4
12 664 8 24 1.0.0.22
13 1292 13 60 1.0.6.1
14 2587 * 4 6 6.40
15 2814 * 22 210 1.1.2.15
16 6619 p 2 2 855
17 6636 29 420 1.0.1.2.18
18 18120 36 840 1.0.0.1.1.33
19 54896 24 240 1.0.0.0.14.6
20 110193 * 9 30 2.7.242
21 153492 13 60 1.0.1.1523
22 358310 * 9 30 1.2.3803
23 645055 * 4 6 3.12075
24 774115 * 4 6 3.14256
25 928993 13 60 6.0.3.43
26 1054187 * 4 6 7.6227
27 1116276 66 4620 1.0.1.2.21.8
28 3029874 * 22 210 1.1.17.936
29 6151929 * 22 210 2.2.17.533
30 9505403 * 4 6 21.12157
31 9635864 17 120 1.0.0.3.15668
32 20648677 * 9 30 4.34.2036
33 23744657 p 2 2 1492085
34 23744691 17 120 2.0.0.26.1002
35 35510476 29 420 1.0.29.24.11
36 63144245 * 9 30 3.26.10922
37 76468986 66 4620 1.1.0.3.26.405
38 182228133 * 4 6 2.3603587
39 242970925 6 12 3.0.647204
40 301284052 6 12 1.0.4412061
41 527247212 6 12 1.0.7475182
42 922682749 p 2 2 47109485
43 922682792 17 120 1.0.0.9.281669
44 1789687069 * 4 6 312.68405
45 1790554184 36 840 1.0.0.16.24.2343
46 3433428185 * 22 210 3.2.31.34837
47 4524447595 * 22 210 3.98.86.47
48 5447808380 66 4620 1.0.2.1.239.2539
49 13083732936 112 27720 1.0.0.1.0.43.29.292
50 35724906776 36 840 1.0.0.5.19.252814
51 72880531169 * 9 30 63.123.18950
52 73184200371 29 420 2.0.5.483.12195
53 111961478488 36 840 1.0.0.12.62.71247
54 215615610241 * 4 6 1139.1474811
55 215639089126 * 9 30 1.223.4436548
56 323685945609 * 54 2310 2.4.3.62.80073
57 486362016603 13 60 2.0.367.1355406
58 702801614161 * 9 30 172.539.11241
59 703625918242 * 54 2310 1.5.4.3.1434109
60 1204499102079 * 54 2310 2.2.2.2828.12781
61 1976702232450 140 60060 1.1.1.0.2.44.366414
62 5371437992314 * 4 6 1.97380324841
63 8057156988592 47 1680 1.0.0.0.12.1279.88674
64 15993014320099 * 4 6 22576.3668578
65 15993076891064 83 9240 1.0.0.3.2.452.460736
66 36918458520028 29 420 1.0.7.1.929390290
67 70964542696933 p 2 2 2299682202677
68 70964542697001 * 9 30 2.2486.54027766
69 94623654599168 135 53760 1.0.0.0.0.0.0.0.0.71.519.10623
70 189634543148505 * 246 510510 2.1.1.2.10.354.80740
71 380630800651340 29 420 1.0.2.7.25078491044
72 826887601416910 * 246 510510 1.2.2.16.9.827.11899
73 1660776753512567 * 22 210 9.55.711.2403134
74 1738852402360531 * 4 6 21.800255166674
75 1762672298283718 * 4 6 1.26402734874534
76 2644008447425725 6 12 3.0.3383476881293
77 3278570474808131 * 4 6 83222.147891573
78 3278573552832629 * 4 6 14.2465088761164
79 3354819449410254 * 54 2310 1.1.2.26922.13977079
80 7668183374333148 140 60060 1.0.1.30.133.420.90305
81 18051715638367929 140 60060 2.0.2.12.30.1427.161434
82 30516976556354361 * 4 6 2.283914755574938
83 40689302075139309 * 54 2310 2.10.81.10225.462356
84 55833618657613217 6 12 17.0.546131076714
85 56795990711468321 * 9 30 36.31856.50976764
86 57172275665472387 * 9 30 2.2.78891085094111
87 87119658156910790 * 9 30 1.2.244212627560152
88 156815384682439753 * 9 30 16.114.144225089321
89 159992138466234122 * 22 210 1.23.2263.1892959251
90 242696700105595456 74 6720 1.0.0.0.0.0.3.474.6454087427
91 550563757314232279 * 4 6 1457.1488592721323
92 550609022771558867 * 4 6 22569723.42523836
93 550609024493197652 29 420 1.0.347.52.941038525
94 964328032845270515 * 9 30 3.444402.1286981732
95 1157193817632780899 * 4 6 33432379.55457969
96 1157193820076048495 * 22 210 3.3.4.18592485425051
97 1547017732939866724 29 420 1.0.9.168803.271563147
98 2800636774575386847 * 9 30 2.205.21990476959740
99 3737101977020068022 * 54 2310 1.24.47.85471.2852813
100 5679224100788214644 13 60 1.0.182484.21896351080
...
Block[{a = {1}, c},
c[1] = 1;
Do[(Map[If[! IntegerQ[c[#] ], Set[c[#], 1], c[#]++] &, #];
AppendTo[a, Total[Map[# c[#] &, #]] ] ) &@ Divisors[a[[-1]] ], 100]; a]]
Concerns OEIS sequences:
A000005: Divisor counting function τ(n).
A007497: a(1) = 2, a(n) = σ(a(n−1)).
A025487: Products of primorials; numbers that are the least instance of a given prime signature.
A027750: Row n contains the divisors d | n.
A046523: Numbers m that are the least number of the same prime signature as n.
A342616: a(1) = 1; a(n+1) = Σ_{d | a(n)} cd, where cd is the number of instances of d | a(k) for 1 ≤ k < n.
Document Revision Record.
2021 0318 2215 Draft.
2021 0406 2100 Publish.