Study of the Ratio of Divisor and Totient Functions for SHCNs

Study of the Ratio of Divisor and Totient Functions for SHCNs

Examination of the ratio σ0(r) / r, with σ0 the divisor counting function, and the totient ratio φ(r) / r, with φ(r) the Euler totient function.

The top chart, “Ratio of Divisor and Totient Function and Superior Highly Composite Number”, plots (σ0(r) / r) / (φ(r) / r) for the smallest superior highly composite numbers. From this, we see there is a breakpoint between 12 and 60, left of which divisors dominate, and right of which, totatives dominate. This illustration indicates to me that bases larger than some point between 12 and 60 would be dominated by resistance via totatives, regardless of how highly divisible they are.

The next chart, “Ratio of Totient Function and Superior Highly Composite Number”, plots φ(r) / r for the smallest superior highly composite numbers. This illustrates that the distinct prime divisors of a number r govern the totient ratio φ(r) / r. At the time the notion was new to me; I’d seen a set of “totient regimes” linked with the smoothness of the SCHN and noted it on the chart. Clearly, each successive distinct prime appended to the set of distinct prime divisors of a SHCN reduces the totient ratio.

The sexagesimal figures at the bottom of the page in the table “Divisor and Totient Functions for the Superabundant Numbers” explore the ability of successively larger SHCNs to minimize the totient ratio. This chart is continued on the next page.

In spring 2018 (tayya a140), I revisited the subject of highly composite and superabundant numbers, resulting in several sequences in the OEIS (A301414, A304234, A304235) that derive from the chart below. This chart derives from plotting highly composite (blue) or superabundant (red) m at (x, y) where the ordered pair represents the largest primorial that divides m, A002110(y) × A301414(x) = m. (The chart has y increasing downward, x increasing rightward).

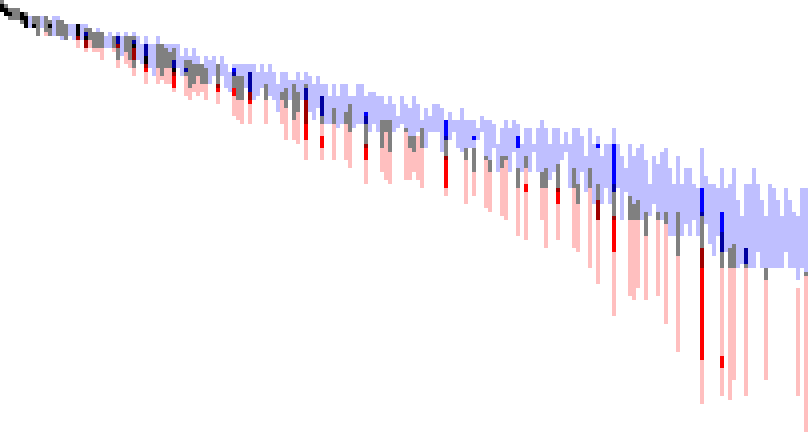
Writ large, this sort of plot illustrates the differences between the highly composite and superabundant numbers:

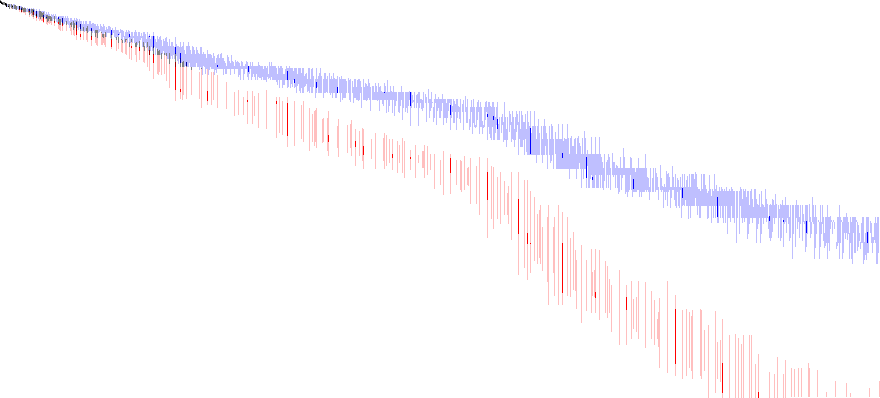
Read more about further examinations of the highly composite and superabundant numbers here.

Written 12 January 2008, tayya 7b25 (Salcyra Lectajinal, “Life Phase of Virtual Solid Order”), St. Louis.

This page last modified Tuesday 15 May 2018.