Study of Totient Ratios and the Diminishing Return of Ever Larger Primorials

Study of Totient Ratios and the Diminishing Return of Ever Larger Primorials

Examination of the ratio of the totient ratio φ(r) / #p, with φ(r) the Euler totient function and #p the primorial with p its largest divisor.

The top left table “Sexagesimal φ/r for Totative Regimes” shows the ratio φ(r) / #p expressed as a sexagesimal digital fraction. This chart shows that the multiplication of #p with ever larger p yields a diminishing effect in the reduction of the totient ratio. This table was studied the day before at s7836b09.

The next table, “Prime Factor Diversity vs. φ/r Ratio” explores the effect of the diversity of prime factors (i.e., the quantity of distinct prime divisors) versus the totient ratio. This table seems to project fields of values that are later illustrated at right.

To the right of the last table, the table “Sexagesimal φ/r for Totative Regimes” compares totient ratios for values of r that have identical sets of distinct prime divisors, showing that they have the same totient ratios.

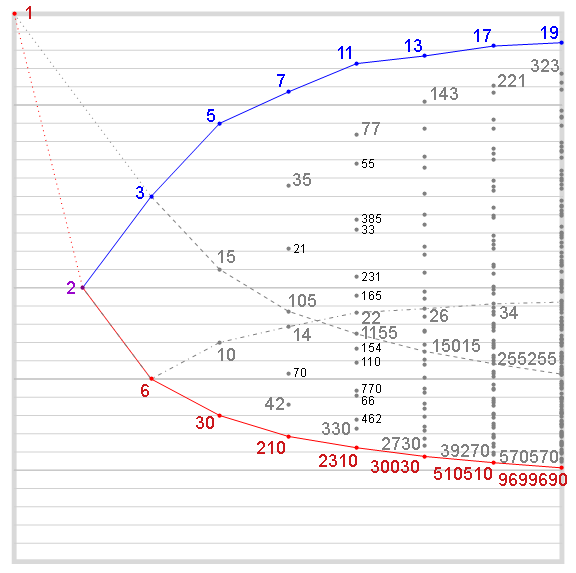
The chart at right, “Prime Factor Diversity vs. φ/r Ratio”, plots the value of φ(r) / r for combinations of products whose largest prime divisor p does not exceed that of the primorial #p. This chart had a great impact on my perception of number bases as tools to minimize resistance caused by totatives. It developed into more refined charts dn34, dn36, and figured into the duodecimal paper “Dozenal FAQs”, d8907.

Written 12 January 2008, tayya 7b25 (Salcyra Lectajinal, “Life Phase of Virtual Solid Order”), St. Louis.

Development into OEIS sequences.

In April 2019 I revisited the totient ratio beyond the 2011 charts. Using Mathematica code I wrote to explore the subject, the chart below corrects some of the errors in the hand-drawn chart. A technical analysis of the totient ratio chart relates it with the three constitutive relationships. The chart developed into the irregular number triangle OEIS A307540 and a binary-coded multiplicity notation version OEIS A307544.



This page last modified Sunday 16 October 2022.