The Marlin Sequence.
Variant of David Sycamore’s “Sailboat Sequence”.
Written by Michael Thomas De Vlieger, St. Louis, Missouri, 2021 0704.
Abstract.
We examine a sequence based on a previous one by David Sycamore that recalls term s(m) for m new to the sequence s, otherwise we write the cardinality of m in s before the introduction of the latest copy of m. This sequence differs from the sailboat sequence principally in that it does not contain the initial term m = 0. Since the records are the natural numbers, the indices of records function as indices of the occasion of recalled s(m) and we may partition s into subsequences t(i) that begin with record m and end with 1. The scatterplot has an interesting bifurcated appearance within the subsequences that inspires us to bisect the subsequences to find interplay between the recursive cardinality functions. We find the occasion of a duplicated term m = h and see that the indices of the subsequences t(i) are the indices k2 of the second appearance of m in s. Therefore we might partition the sequence s into supersequences T(K) where the first subsequence in the supersequence contains a duplicated term h. We also consider a secondary subsequence based on partition of s by k2. There are interesting connections between subsequence lengths in a supersequence and the terms in the corresponding secondary subsequence. This seems to explain a “marlin” or “sailboat” shaped void in the large-scale scatterplot of s, depending on the aspect ratio of the plot.
Review the summary: click here.
Introduction.
Let s(1) = 1; If s(n) = s(k) for 1 ≤ k < n , then s(n+1) = c(s(n)) where c(m) is the cardinality of m in s(1..n − 1), else s(n+1) = s(s(n)).
Sycamore’s original concept used offset 0, and set s(0) = 0. See The Sailboat Sequence for more on this concept, however, in that paper we used an offset of 1 rather than 0.
The sequence s begins:
1, 1, 1, 2, 1, 3, 1, 4, 2, 1, 5, 1, 6, 3, 1, 7, 1, 8, 4, 1, 9, 2, 2, 3, 2, 4, 2, 5, 1, 10, 1, 11, 5, 2, 6, 1, 12, 1, 13, 6, 2, 7, 1, 14, 3, 3, 4, 3, 5, 3, 6, 3, 7, 2, 8, 1, 15, 1, 16, 7, 3, 8, 2, 9, 1, 17, 1, 18, 8, 3, 9, 2, 10, 1, 19, 4, 4, 5, 4, 6, 4, 7, 4, 8, 4, 9, 3, 10, 2, 11, 1, 20, 1, 21, 9, 4, 10, 3, 11, 2, 12, 1, 22, 2, 13, 1, 23, 2, 14, 1, 24, 3, 12, 2, 15, 1, 25, 2, 16, 1, ...
s(2) = 1 since s(1) = 1 sets a record in s (hence is new) therefore we recall s(s(1)) = s(1) = 1.
s(3) = 1 since s(2) = s(1) = 1; m = 1 appears once in s(1..1).
s(4) = 2 since s(3) = s(1) = s(2) = 1; m = 1 appears twice in s(1..2).
s(5) = 1 since s(4) = 1 sets a record in s (hence is new) therefore we recall s(s(4)) = s(2) = 1.
s(6) = 3 since m = 1 appears thrice in s(1..4).
s(7) = 1 since s(6) = 3 sets a record in s (hence is new) therefore we recall s(s(6)) = s(3) = 1.
s(8) = 4 since there are 4 copies of m = 1 in s(1..6).
s(9) = 2 since s(8) = 4 sets a record in s (hence is new) therefore we recall s(s(8)) = s(4) = 2.
s(10) = 1 since s(9) = s(4) = 2; m = 2 appears once before s(9).
etc.
This sequence can be generated by Code 1. We have generated 220 terms.
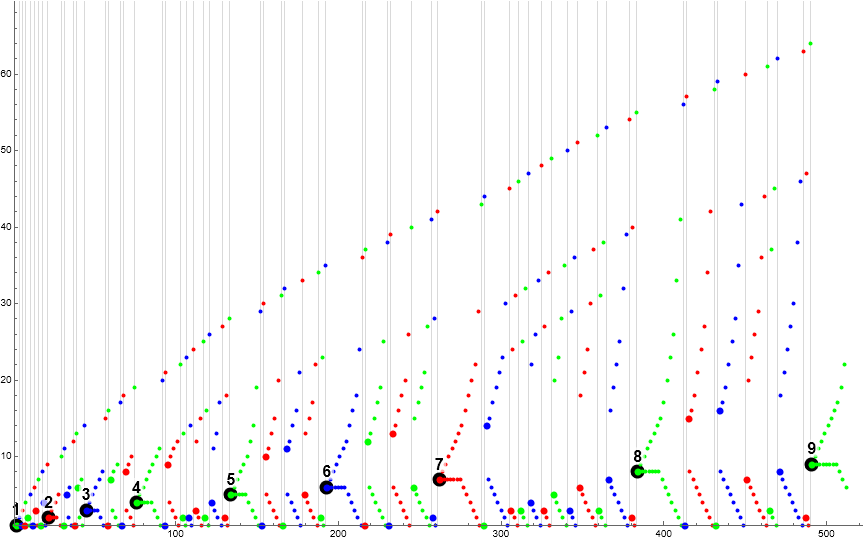
Figure 1.1 is a scatterplot of s(n) for 1 ≤ n ≤ 28. Red points are records, large gold points are the result of Condition 0, green are fruits of Condition 1. Click for a scatterplot of s(n) for 1 ≤ n ≤ 220.
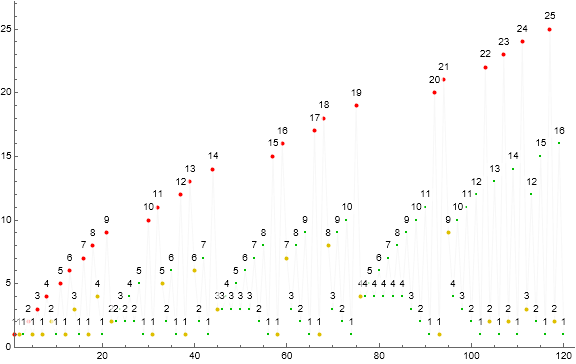
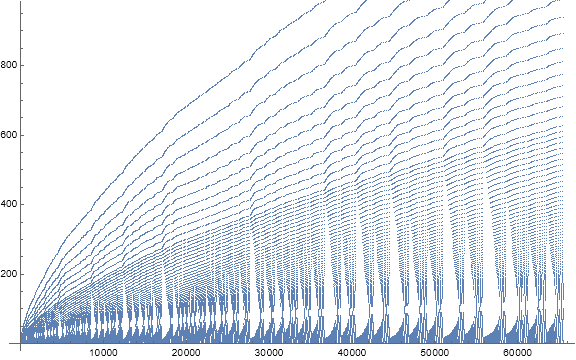
Figure 1.2 is a scatterplot of s(n) for 1 ≤ n ≤ 216.
Let b(n) = 1 if s(n) = s(k) for k < n else let b(n) = 0. Hence we have a characteristic function of the occasion of m in s at a smaller index. The sequence b begins:
0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, ...
It is evident that we have many runs of 1s but 0 is singleton. Taking the indices k0 of 0 in b, we have:
1, 4, 6, 8, 11, 13, 16, 18, 21, 30, 32, 37, 39, 44, 57, 59, 66, 68, 75, 92, 94, 103, 107, 111, 117, 121, 129, 133, 152, 154, 165, 167, 178, 188, 192, 215, 217, 230, 232, 245, 257, 261, 288, 290, 305, 311, 317, 325, 331, 341, 347, 359, 365, 379, 383, 412, 414, 431, 433, 450, ...
The first differences ℓ are:
3, 2, 2, 3, 2, 3, 2, 3, 9, 2, 5, 2, 5, 13, 2, 7, 2, 7, 17, 2, 9, 4, 4, 6, 4, 8, 4, 19, 2, 11, 2, 11, 10, 4, 23, 2, 13, 2, 13, 12, 4, 27, 2, 15, 6, 6, 8, 6, 10, 6, 12, 6, 14, 4, 29, 2, 17, 2, 17, 14, 6, 16, 4, 33, 2, 19, 2, 19, 16, 6, 18, 4, 37, 2, 21, 8, 8, 10, 8, 12, 8, 14, 8, 16, 8, 18, 6, 20, 4, 39, 2, 23, 2, 23, 18, 8, 20, 6, 22, 4, 43, 2, 25, 4, 45, 2, 27, 4, 47, 2, 29, 6, 24, 4, 49, 2, 31, 4, 51, ...
We shall consider partitioning s into subsequences t(i) = s(k…k+ℓ−1) where s(k) is new to s and the remaining terms are already in s.
Maxima and minima.
Records R are common and the list of records is that of the natural numbers. The indices of records Ri are:
1, 4, 6, 8, 11, 13, 16, 18, 21, 30, 32, 37, 39, 44, 57, 59, 66, 68, 75, 92, 94, 103, 107, 111, 117, 121, 129, 133, 152, 154, 165, 167, 178, 188, 192, 215, 217, 230, 232, 245, 257, 261, 288, 290, 305, 311, 317, 325, 331, 341, 347, 359, 365, 379, 383, 412, 414, 431, 433, 450, 464, 470, 486, 490, 523, 525, 544, 546, 565, 581, 587, 605, 609, 646, 648, 669, 677, 685, 695, 703, 715, 723, 737, 745, 761, 769, 787, 793, 813, 817, 856, 858, 881, 883, 906, 924, 932, 952, 958, 980, 984, 1027, 1029, 1054, 1058, 1103, 1105, 1132, 1136, 1183, 1185, 1214, 1220, 1244, 1248, 1297, 1299, 1330, 1334, 1385, ...
Hence the records represent the sole manifestation of novel m. In other words, if s(n) ≠ s(k), then s(n) has set a record, the previous record is s(n) − 1, and the next s(n) + 1. The numbers in bold are in Rh and shall be described below.
We see that Ri ≡ k0, since records m represent the only novel m in s. Hence (ℓ − 1) represents the run lengths of Condition 1 in s. We might partition s into subsequences t(i) = s(k…k+ℓ), where k is an index of a zero in b, i.e., k ∈ k0.
We know that there cannot be adjacent records m, since records are novel, thus trigger Condition 0 which reports s(m). Once we have adjacent identical m < 1, Condition 0 yields s(m) ≤ m. As a consequence, we cannot have adjacent records, and s(n) < n for n > 1.
The minimum of s is 1. The triplicated 1 that starts the sequence is the only occasion of three consecutive identical m in s. This is because 1 → s(1) = 1 ⇒ s(2) = c(1) = 1.
The most common term M = 1 in s. This is because 1 represents the ultimate end of the recursion of Condition 1 that follows a single instance of Condition 0.
There are two sources of m' in the sequence, of course, those novel m → s(m) = m', and those extant m ⇒ c(m) = m', where “→” represents Condition 0 and “⇒” Condition 1. Since the novel m must be records, we may restate Condition 1 as record R = m → s(m) = m', or even, the first instance of m → s(m) = m'. By the last statement it is clear that all terms m in s are restated at least once as n increases.
Thus, there are 1s that result from new m and are thus Condition 0 reflections of s(m), and there are 1s that derive from extant m that report the total number of instances of m that have come before m in s. Since every m appears at least once in the sequence, and since the first appearance must be a record, the s(n) such that s(n) → 1 strictly increase as n increases; these are reflections of previous 1s. When s(n) = s(k) for k < n, we have s(n) ⇒ 1 for the second appearance of s(n).
We note record R' = R + 1, where R' is the record that replaces R. The appearance of commonest term M = 1 ⇒ c(M) = R → s(R). Hence the action of Condition 0 that applies only to records R recreates s(n) at s(k) for k > n. Let M = s(i); then s(i−1) = R and generally, s(i−1) for 1 ≤ i recreates the natural numbers, and the sequence s(i+1) for 1 ≤ i recreates s(n) for 1 ≤ n. This is equivalent to saying s(Ri+1) = s(i) and the sequence of fruits of Condition 0, s(Ri+2) = s(n).
Subsequences t(i).
Since we have a single instance of Condition 0 followed by (ℓ−1) ≥ 1 of iterations of Condition 1, we can partition the sequence into subsequences t(i) = s(k…k+ℓ−1) according to condition. Such subsequences begin with a reflected term s(s(k)), followed by iterations of cardinalities m ⇒ c(m).
Subsequence t(i) begins with s(k) = R = i → s(k+1) = s(i). In other words, the first term in subsequence t(i) is i itself, since the i-th record is indeed i itself, and since Condition 0 reports the term s(m) and m = i, we have the i-th term in s appear again at s(k+1). Subsequence t(i) ends with s(k+ℓ−1) = 1, which is the commonest M in s, hence has the greatest cardinality c(M) and exceeds that set by 1 in the previous subsequence t(i−1) by 1, therefore sets a record R' = R + 1, that is the first term of subsequence t(i+1).
For R = 1, s(R) = 1 and then c(R) = 1, hence t(1) = {1, 1, 1}. For i > 1, R > s(R) by definition of “record”. The second appearance of s(n) occurs in subsequence t(n) = {n, s(n), 1} with length ℓ = 3, since in t(n), c(s(n)) = 1.
The first subsequences are:
1 → 1 ⇒ 1 ⇒
2 → 1 ⇒
3 → 1 ⇒
4 → 2 ⇒ 1 ⇒
5 → 1 ⇒
6 → 3 ⇒ 1 ⇒
7 → 1 ⇒
8 → 4 ⇒ 1 ⇒
9 → 2 ⇒ 2 ⇒ 3 ⇒ 2 ⇒ 4 ⇒ 2 ⇒ 5 ⇒ 1 ⇒
10 → 1 ⇒
11 → 5 ⇒ 2 ⇒ 6 ⇒ 1 ⇒
12 → 1 ⇒
13 → 6 ⇒ 2 ⇒ 7 ⇒ 1 ⇒
14 → 3 ⇒ 3 ⇒ 4 ⇒ 3 ⇒ 5 ⇒ 3 ⇒ 6 ⇒ 3 ⇒ 7 ⇒ 2 ⇒ 8 ⇒ 1 ⇒
15 → 1 ⇒
16 → 7 ⇒ 3 ⇒ 8 ⇒ 2 ⇒ 9 ⇒ 1 ⇒
...
We see that if R → s(R) = 1, then the subsequence terminates with ℓ = 2.
Figure 3.1 is a scatterplot of s(n) for 1 ≤ n ≤ 216, showing the subsequences in a color function i (mod 5). The labels are not s(n) but s(n−1) so as to illustrate the Condition 1 trajectories. The large colored dots indicate the fruits of Condition 0, i.e., record m → s(m), a recalled value. The large black dots accentuate the first term is an occasion of a duplicated m.
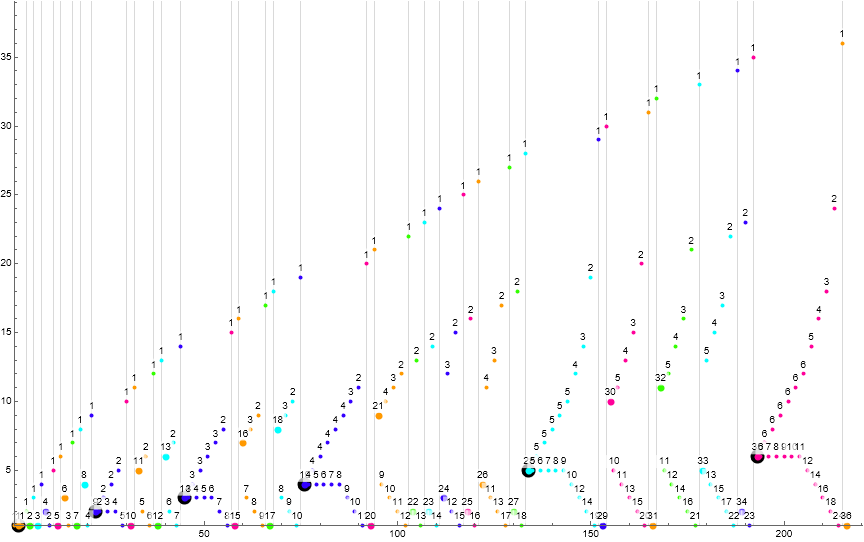
The scatterplot Figure 3.1, seen in the light of subsequences t(i), reveals 4 principal features of the sequence s.
- Arrangement of s into subsequences t(i). The novel instigator s(k) → s(k+1) may be rewritten R → s(R) or further i → s(i). Thus the number s(k) = i initiates a subsequence t(i) followed by s(k+1) < i for i > 1. Thereafter, within the subsequence t(i) = s(k…k+ℓ−1), Condition 1 m ⇒ c(m) iterates recursively until we have s(k+ℓ−1) = 1. If i → s(i) = 1, ℓ = 2, or if s(i) ⇒ c(s(i)) = 2, ℓ = 3, else, ℓ > 3.
- Trajectories c(m). Since s(k+1) < s(k), the subsequent c(m) increment with the reiteration of small m. Hence we have the trajectories c(m) resulting from the recursion of Condition 1 in subsequence t(i). The trajectories c(m) for m ≥ 1 are plain to see as n increases. In a large scatterplot they take on a scalloped shape as n increases. Consider the j-th appearance of c(m) = v. The (j + 1)-th appearance of c(m) = v + 1. Therefore the commonest M sets records R = c(M), and the union of s(1..k) where s(k) = c(m) represents the natural numbers [1 … R].
- “Herringbone” numbers h. There is a pattern in certain subsequences t(i) wherein s(k+1) = s(k+2) = s(k+4) = … = s(k + 2(L−1)). This situation has c(s(k)) increment L times including s(k+1) = c(s(k+1)). We shall refer to such numbers as herringbone numbers hi = c(hi) in subsequence t(i) with repetition length L and instigator m → hi.
- Bisection of subsequences t(i) reveals a “preferential reverse indexing” of m ≤ h subsequence position s(k + ℓ − 2m + 1). We find that m = 1 appears in t(i) at s(k+ℓ−1), i.e., the last term of subsequence t(i). Additionally, for sufficiently large i, we find m = 2 appears at s(k + ℓ − 3), i.e., the 3rd from last term in t(i), and m = 3 at s(k + ℓ − 5), 5th from last, etc. Hence, we have m ⇒ c(m) intercalated between these odd negative-indexed terms. This is responsible for the “butterflying” effect, where negatively-indexed even terms appear on the large end, and negatively-indexed odd terms appear on the small end of the range m (i.e., the y-axis in the scatterplot).
Infinite restatement of m in s.
Condition 0 triggers the algorithm novel m → s(m), a recall algorithm. Since the only novel m in s are its records R, the index (m + 1) increases as n increases, such that we have progressively later terms recalled into s. Furthermore, every term s(m) is reverberated later in the sequence through induction on account of R.
Therefore, for sequence s, we have the transformation of the sequence Ri → R = k0 → N1. Certainly, the indices of records map to records, therefore the indices of Condition 0, i.e., novel m, map to the nonnegative numbers. Ultimately, Ri → N1.
A consequence of the inverse of this transformation is s(k) reappears at s(n) for n in Ri. We can reconstruct s using the terms s(n) for n in Ri. This is tantamount to s(n) = s(k+1) in t(n), that is, s(n) is reiterated in the second term of subsequence t(n).
Let us for the moment assume the recursion of Condition 1 between Condition 0 is finite, hence 1 < ℓ < ∞.
The reproduction of m = s(k) at s(n) for n in Ri implies that m ≥ 1 will appear an infinite number of times in s on account of induction on R and the fact Ri > R. The effect of Condition 1 merely places additional instances of m ≥ 1 in s to be reverberated later in the sequence.
The sequence s would prove infinite since all terms are reflected at some later point following records that are the nonnegative integers. The reappearance of extant m = 1 ⇒ c(1) = R, which is 1 greater than the last record R and by definition new to s, recalling the next term in s.
If Condition 1 or ℓ is infinite after a certain k, then we will see no further records R. However, Condition 1 involves the report of the cardinality c(m) of m in s(1..n−1). Therefore, suppose we have an infinite identical m in s. The report of m necessitates c(m) between instances, therefore adjacent m cannot be sustained. We would have m ⇒ m ⇒ m + 1. Ignoring this, at some point, c(m) > R and thereby triggers Condition 0, ending the run of Condition 1, a contradiction. Suppose we never repeat m in subsequence t(i). We know that 1 ≤ m ≤ R, therefore we know that such a prohibition entails 1 < ℓ ≤ R + 1, contradicting an infinite run of Condition 1. Finally, suppose that we may repeat any 1 ≤ m ≤ R infinitely. If we repeat any m in a finite range infinitely, we report the cardinality c(m), which obviously increments for each appearance of m, therefore some of the m in the run must be cardinalities of other m. However, at a certain point c(m) > R for some m, triggering Condition 0 and ending the run, a contradiction. Hence, Condition 1 cannot be repeated after Condition 0 in subsequence t(i) indefinitely, and ℓ is in fact finite.
Therefore s is infinite and contains an infinite number of copies of any distinct term m; the records R are the natural numbers. All m have trajectories in s, all cardinalities c(m) increase to infinity, and there are an infinite number of subsequences that begin with Condition 0 on account of the occasion of a final 1 in the previous subsequence for i > 1, etc.
It is interesting to find the indices k2 of the second occurrence of m in s, as these relate to the occasion of the herringbone numbers h:
2, 9, 14, 19, 28, 35, 42, 55, 64, 73, 90, 101, 105, 109, 115, 119, 127, 131, 150, 163, 176, 186, 190, 213, 228, 243, 255, 259, 286, 303, 309, 315, 323, 329, 339, 345, 357, 363, 377, 381, 410, 429, 448, 462, 468, 484, 488, 521, 542, 563, 579, 585, 603, 607, 644, 667, 675, 683, 693, 701, 713, 721, 735, 743, 759, 767, 785, ...
We might partition s into “secondary subsequences” according to the indices k2 and derive a series of lengths ℓ2:
1, 7, 5, 5, 9, 7, 7, 13, 9, 9, 17, 11, 4, 4, 6, 4, 8, 4, 19, 13, 13, 10, 4, 23, 15, 15, 12, 4, 27, 17, 6, 6, 8, 6, 10, 6, 12, 6, 14, 4, 29, 19, 19, 14, 6, 16, 4, 33, 21, 21, 16, 6, 18, 4, 37, 23, 8, 8, 10, 8, 12, 8, 14, 8, 16, 8, 18, 6, 20, 4, 39, 25, 25, 18, 8, 20, 6, 22, 4, 43, 27, 4, 45, 29, 4, 47, 31, 6, 24, 4, 49, 33, 4, 51, 35, 8, 22, 6, 26, 4, 53, 37, 4, 55, 39, 10, 10, 12, 10, 14, 10, 16, 10, 18, 10, 20, 8, 24, 6, 28, ...
Of course we might find indices of the third (k3), fourth (k4), etc. m in s. This is a brief list of indices k3 of the third m in s:
3, 22, 24, 26, 33, 40, 53, 62, 71, 88, 99, 113, 125, 148, 161, 174, 184, 211, 226, 241, 253, 284, 301, 307, 313, 321, 327, 337, 343, 355, 361, 375, 408, 427, 446, 460, 466, 482, 519, 540, 561, 577, 583, 601, 642, 665, 673, 681, 691, 699, 711, 719, 733, 741, 757, 765, 783, 789, 809, 852, ...
Trajectories of c(m).
The prominent striations that appear to emanate in an irregular way from origin are a manifestation of the trajectories of c(m) for m > 0, attributable to the predominant Condition 1 provenance of most of the terms in the sequence.
We speak of trajectories since we report m ⇒ c(m), and obviously for each new occasion of m in s, c(m) increments. If the reporting of a particular m ⇒ c(m) occurs frequently enough, to the eye, it seems to produce a stream in the scatterplot..
The cardinality of a particular m is not always reported into s; at times m enters s via Condition 0. This introduces imperfections in an otherwise orderly progression of any striation attributable to c(m). Indeed, m enters s through Condition 0 an infinite number of times, only much less frequently for small m than through Condition 1.
Since s is infinite and contains infinite copies of m in the nonnegative integers, we may trace the cardinality of any 0 ≤ m < R in s(1..n) as n increases.
Figure 5.1 is a scatterplot of s(n) for 1 ≤ n ≤ 28, labeling s(n) instead with s(n−1) = m, the progenitor of s(n). We apply a color function m (mod 8) to represent the fruits of Condition 1 m ⇒ c(m) with small dots. The fruits of Condition 0, m → s(m) appear in large black dots, rehashing s in order of appearance and delimiting the subsequences t(i). Evident in the scatterplot are the trajectories of 1 through 5, with larger m less visually apparent at this range.
We could expect the crossing of trajectories as the cardinality of c(m) overtakes c(m') for m ≠ m'. The large scale scatterplot seems to suggest that the trajectories do not cross, hence, the cardinality c(m) > c(m') for 1 < m < m'. What makes the trajectories for m ≥ 1 stay in their lanes?
The records R in s increment as n increases, albeit in an irregular, discontinuous fashion. This suggests that the numbers m in s are introduced in order. A second appearance through either condition certainly happens by definition after the first, hence c(1) ≥ c(2). Hence the trajectories must roughly remain in their lanes, but certainly so as n increases.
Herringbone numbers h.
In fact, the situation of greater cardinality for smaller m ≥ 1 intensifies as n increases.
Suppose we begin a subsequence t(i), i ≥ 2, with s(k) = i such that s(k+1) = s(i) = 1. We have s(k+1) = 1 ⇒ ci(1) > c(i−1)(1), and thus a record in s(k+2), hence novel s(k+2) and the subsequence ends via s(ci(1)) = s(i + 1) via Condition 0. We know that 1 terminates the subsequence t(i) because it is commonest term M and thus its cardinality sets a record (by definition).
Now suppose that we have s(k+1) = s(i) = m “low”. Since m is small, it is more common and a “high” number c(m) will follow. But this “high” m is not common so it is followed by a low c(m). The low and high numbers may alternate.
Alternating low and high numbers eventually set a record when the low m = 1, triggering Condition 0 and ending the subsequence t(i).
Suppose that we have s(k+1) = s(i) = h such that c(h) = h. Then we have h ⇒ h ⇒ (h+1), that is, 2 consecutive identical terms h. From this point, perhaps since (h+1) > h, c(h+1) < h, and hence we have alternating low and high numbers. It is also likely that we might have h ⇒ h ⇒ (h+1) ⇒ h ⇒ (h+2), etc. At a certain point, the intervening high m will trigger interleaved progressively lower m until m = 1. Indeed that certain point is the (h+1)-th appearance of h in s.
Because each m appears infinite times in s, and because smaller m appear before larger m, all m will be duplicated as h, and smaller m will be duplicated before larger m are duplicated.
Let h(K) be the K-th herringbone number, so named for the appearance of the term in the scatterplot. The indices Rh for herringbone numbers are:
1, 21, 44, 75, 133, 192, 261, 383, 490, 609, 817, 984, 1058, 1136, 1248, 1334, 1486, 1580, 1884, 2149, 2430, 2658, 2776, 3216, 3581, 3964, 4282, 4424, 5024, 5503, 5713, 5929, 6203, 6431, 6769, 7009, 7411, 7663, 8129, 8321, 9101, 9762, 10445, 10975, 11271, ...
The indices H of the subsequences t(H) that harbor a herringbone number h(K):
1, 9, 14, 19, 28, 35, 42, 55, 64, 73, 90, 101, 105, 109, 115, 119, 127, 131, 150, 163, 176, 186, 190, 213, 228, 243, 255, 259, 286, 303, 309, 315, 323, 329, 339, 345, 357, 363, 377, 381, 410, 429, 448, 462, 468, ...
It is evident that H > 1 correspond with the indices k2 of the second occasion of m in s.
The 2 terms that follow the first term of t(Rh) in s are the herringbone numbers h(K).
R(Rh) → h ⇒ h ⇒ …
Like the records R, the herringbone numbers are identical to the natural numbers. Hence, every m ≥ 1 seems to be a herringbone number h(K) at s(H+1) = s(Hk+2) = s(H+4) = … = s(H + 2(L−1)). This implies that the artifact of h occurs as a result of the occasion of h = s(k) < s(H+1) via c(m) for m < h. At some point we have s(k+1) = s(k+2) = c(h(K)), that for s(k+1) > h(K), s(k+2) = c(s(k+1)) < h(K), and for s(k+1) < h(K), s(k+2) = c(s(k+1)) > h(K). It is only when s(k+1) = h(K+1) = s(k+2) = c(s(k+1)).
Figure 6.1 is a scatterplot of s(n) for 1 ≤ n ≤ 29, with a color function that highlights subsequence i (mod 3). The large black circles show the instance of a pattern {h, h}, i.e., adjacent duplicated terms h.
There is one triplicated h = 1 in t(1) = {1, 1, 1}, via novel 1 → s(1) = 1 ⇒ c(1) = 1. No further triple h are possible.
The first duplicated h appears in t(2) = s(21…29), where we have Q = 4 reiterations of s(k+1) = 1 following the first.
Table 6.1 is a list of the first 8 cases of duplicated h. The term h = s(k+1).
H k Q c(i) = s(k..(k+ℓ−1))
---------------------------------
1 1 3 {1, 1, 1}
9 21 4 {9, 2, 2, 3, 2, 4, 2, 5, 1}
14 44 5 {14, 3, 3, 4, 3, 5, 3, 6, 3, 7, 2, 8, 1}
19 75 6 {19, 4, 4, 5, 4, 6, 4, 7, 4, 8, 4, 9, 3, 10, 2, 11, 1}
28 133 6 {28, 5, 5, 6, 5, 7, 5, 8, 5, 9, 5, 10, 4, 12, 3, 14, 2, 19, 1}
35 192 7 {35, 6, 6, 7, 6, 8, 6, 9, 6, 10, 6, 11, 6, 12, 5, 14, 4, 16, 3, 18, 2, 24, 1}
42 261 8 {42, 7, 7, 8, 7, 9, 7, 10, 7, 11, 7, 12, 7, 13, 7, 14, 6, 16, 5, 18, 4, 20, 3, 22, 2, 29, 1}
...
The greatest Q = 57 for 1 ≤ n ≤ 220, starting with s(1047574) = 8867 followed by h = 346.
An example of a subsequence with repeating h is t(73):
73 ⇒ 10 ⇒ 10 ⇒ 11 ⇒ 10 ⇒ 12 ⇒ 10 ⇒ 13 ⇒ 10 ⇒ 14 ⇒ 10 ⇒ 15 ⇒ 10 ⇒ 16 ⇒ 10 ⇒ 17 ⇒ 10 ⇒
18 ⇒ 10 ⇒ 19 ⇒ 9 ⇒ 21 ⇒ 8 ⇒ 24 ⇒ 7 ⇒ 27 ⇒ 6 ⇒ 30 ⇒ 5 ⇒ 33 ⇒ 4 ⇒ 36 ⇒ 3 ⇒ 45 ⇒ 2 ⇒ 55 ⇒ 1 →
In this subsequence h = 10 is repeated Q = 10 times at s(k…s(k + 2(L−1))). Furthermore, we have m with identical c(m) in a range has identical cardinalities. The action of such a subsequence is to build a “cliff” c(h) and a “plain” c(m) for m in {(h+1)…(h+L−1)}. Observations show that Q is nondecreasing as k increases.
We may take a snapshot of the values of cardinalities c(m) for 1 ≤ m ≤ R at the subsequence where we have h = 10, i.e., t(73) = s(609..645) = {73, 10, 10, 11, 10, …, 1}, we list such cardinalities:
74, 55, 45, 36, 33, 30, 27, 24, 21, 10, 10, 10, 10, 10, 10, 10, 10, 10, 9, 9, 8, 8, 8, 7, 7, 7, 6, 6, 6, 5, 5, 5, 4, 4, 4, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
Figure 6.2 is an annotated scatterplot of the cardinalities c(m) for 1 ≤ m ≤ R at s(609).
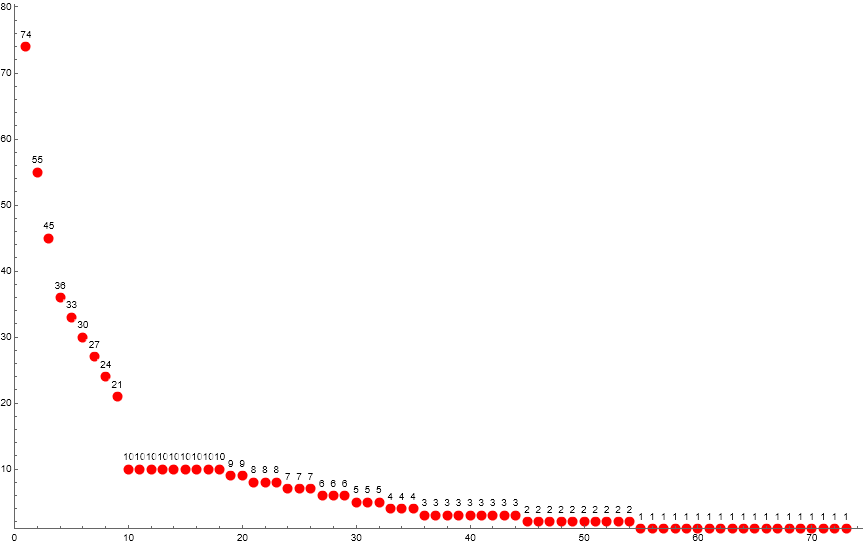
The cardinalities generally grade down as m increases, however we see c(10..18) = 10. The cardinalities feature a “gutter” that includes the “cliff” c(9) = 21 followed by the “plain” c(10..18).
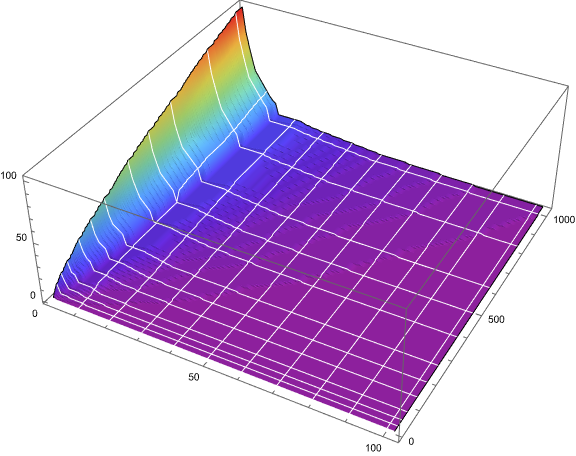
Figure 6.2 is a 3-dimensional plot of s(n) for 1 ≤ n ≤ 210, on the y-axis at right, 1 ≤ m ≤ 101 on the x-axis at bottom, and the color function and height representing c(m) at left. The white gridlines that move left to right “down” the slope correspond to s(k) that start t(i) with duplicated h; t(73) appears just beyond the tick corresponding to n = 600 on the right (y) axis. The “gutter” is a prominent feature of the snapshots of the range of cardinalities.
Bisection of subsequences t(i).
We can examine other patterns in the series of subsequences, among terms justified in reverse to the end of the subsequence. When we see the patterns laid out in this way, many things make sense about the scatterplot. We shall use a reverse index j that counts down from (k+ℓ−1) toward k.
Let subsequence bisection a1 include terms s(k+ℓ−j) in subsequence t(i) with odd 1 ≤ j ≤ ℓ and let subsequence bisection a2 have even j. We note that s(k+0) = i, s(k+1) = s(i), s(k+2) = c(s(i)), etc., and for i ≥ 1, s(k+ℓ−1) = 1.
The terms a1(j/2) begin with 1 and usually increase to 2, 3, 4, etc., while the terms a2((j−1)/2) are much larger, falling from a record a2(0) = s(k) that is the first term of the subsequence t(i+1). As j increases, a1 and a2 approach one another. The pattern is plainer to see in the table below.
Table 7.1. A list of terms in subsequence t(i) presented in reverse, starting with term j = 1, meaning s(k+ℓ−1), the last term which is 1 for i > 2, and proceeding backward toward term j = ℓ, meaning s(k) = i, the first term. The penultimate term j = (ℓ− 1) in the reversed subsequence, s(k+1) = s(i). We bold terms in the odd bisection a1 (which are on the “low” end) and those in the even bisection a2 (which are figures on the “high” end). We place in parentheses repeated h, and the record R = (i − 1) that starts the subsequence t(i).
k i 1 2 3
------------------
1 1 1 1 [1]
4 2 1 [2]
6 3 1 [3]
8 4 1 2 [4]
11 5 1 [5]
13 6 1 3 [6]
16 7 1 [7]
18 8 1 4 [8]
21 9 1 5 2 4 2 3 2 2 [9]
30 10 1 [10]
32 11 1 6 2 5 [11]
37 12 1 [12]
39 13 1 7 2 6 [13]
44 14 1 8 2 7 3 6 3 5 3 4 3 3 [14]
57 15 1 [15]
59 16 1 9 2 8 3 7 [16]
66 17 1 [17]
68 18 1 10 2 9 3 8 [18]
75 19 1 11 2 10 3 9 4 8 4 7 4 6 4 5 4 4 [19]
92 20 1 [20]
94 21 1 12 2 11 3 10 4 9 [21]
103 22 1 13 2 [22]
107 23 1 14 2 [23]
111 24 1 15 2 12 3 [24]
117 25 1 16 2 [25]
121 26 1 17 2 13 3 11 4 [26]
129 27 1 18 2 [27]
133 28 1 19 2 14 3 12 4 10 5 9 5 8 5 7 5 6 5 5 [28]
152 29 1 [29]
154 30 1 20 2 15 3 13 4 11 5 10 [30]
165 31 1 [31]
167 32 1 21 2 16 3 14 4 12 5 11 [32]
178 33 1 22 2 17 3 15 4 13 5 [33]
188 34 1 23 2 [34]
----------------------------------------------------------------------------------
k i 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Let us ignore the bracketed term that appears last in Table 7.1, for it is clear that s(k) = i.
Firstly, we see that a1 contains m in order as j increases, but that m must be introduced by repetition as h. Furthermore, the increasing, ordered portion of a1 lengthens by 1 whenever h appears.
Secondly, we see that if s(i) = 1 for i > 3, then we have the shortest possible subsequence t(i) with length ℓ = 2. Plainly, R → 1 ⇒ R', thus the subsequence ends. There is a relationship of the magnitude of s(i) (for sufficiently large i) and ℓ, but locally longest subsequences pertain to those with h.
Thirdly, quite naturally, for the ordered portion of a1 = s(k+ℓ−(2j−1)) that features incrementing m, we seem to have “reverse-cardinalities” that follow in a2 = s(k+ℓ−2j) that increment as i increments so long as s(k+ℓ−2j) ≠ i, or, rather,ℓ ≠ 2j. Therefore, both s(k+ℓ−(2j−1)) and s(k+ℓ−2j) must not equal i in order for the reverse-cardinality to “count” or “qualify”.
It seems that any given m appears such that c(m) = m hence we have repeated m = h. This would imply that m appears m times by the time we have repeated h. This makes sense since such repetition as {h, h} cannot otherwise occur. We observe that there are occasions of m with c(m) = (m − 1) in preceding subsequences that have the progression out of focus and the bisections immediately diverge.
Therefore we have R → s(i) that happens to resonate with a range of m that have identical c(m); the c(m) increase as n increases, but more markedly for small m, and each m see duplication as {h, h}. The situation propagates as n increases, with L nondecreasing as h increases. If it weren’t for the duplication of h, we would see the latest R in a run of intercalated records set a record for ℓ.
We can employ h as the index of an occasion of duplicated h in subsequence t(Rh). Outside of t(Rh), for Rh < i < Rh', the longest possible subsequence t(i) has length ℓ = 2h + 1. This subsequence is t(Rh + 2), possibly followed in certain Rh by t(Rh + 4) with the same length.
In a strange way, given s(k+ℓ−j) with j odd, after m having been duplicated, C(m) =s(k+ℓ−(2j−1)) functions as the cardinality of m = s(k+ℓ−2j) in s that haven’t immediately followed the first term s(k) = i of the subsequence t(i). Suppose we have h ⇒ c(h) = h at subsequence t(i), i.e., duplicated h. If we have J subsequences between the h-th occasion and the (h+1)-th occasion of duplicated h that have the maximum ℓ = 2h + 1, then when h' = (h+1) arises, we find that the “reverse cardinality” of h = h + J, and hence L' = J + 3.
The development of the “cliff” and “plain” that creates a “gutter” among the cardinalities at n seems to arise when we have h appear. The multiple copies of h send that m into a cliff (markedly increasing cardinality) and broaden the plain of identical cardinalities. We see that m < h appear in every subsequence with ℓ = 2m − 1, while not all h > m ≥ R appear in t(i).
Supersequences T(K).
We shall use a separate index K to denote the instances of duplicated h to eliminate confusion. In this way, we build “supersequences” of subsequences delimited by the “herringbone” record Rh that generates duplicated h.
T(K) contains subsequences t(N) for Rh(K) ≤ N < Rh(K+1).
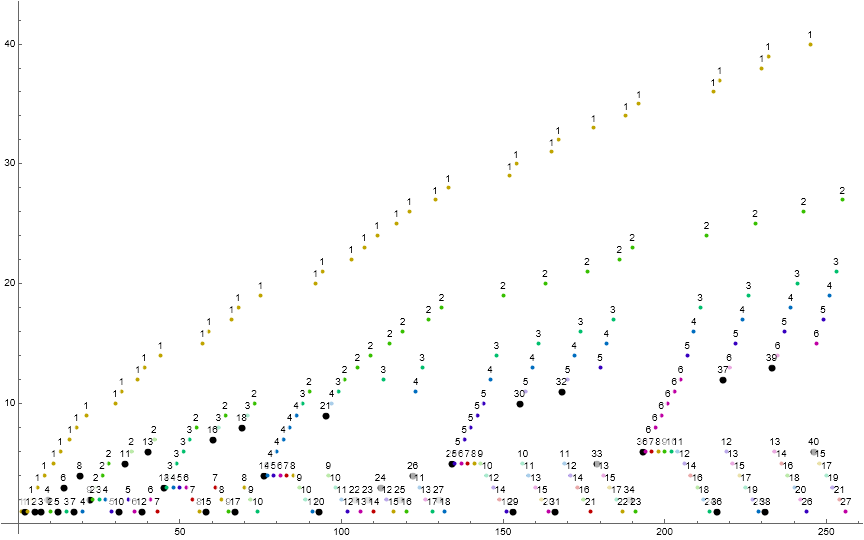
Figure 8.1: Scatterplot of supersequence T(10) = t(73..89) = s(609..816). Red indicates records 73 ≤ R ≤ 89, green the terms that result from Condition 0 recall, i.e. R → s(R), gold indicating h = 10, and blue indicating m = 1. The gray gridlines are struck at each record, thus the t(N) in supersequence T(10).
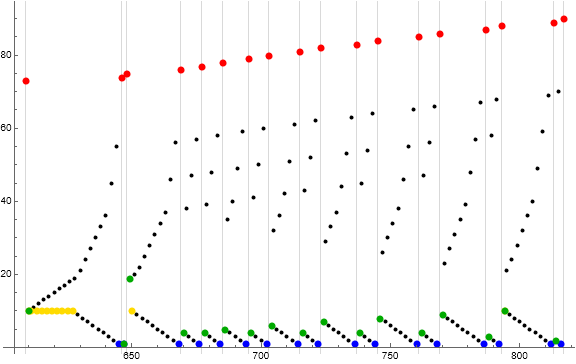
The m plotted include all the following:
73, 10, 10, 11, 10, 12, 10, 13, 10, 14, 10, 15, 10, 16, 10, 17, 10, 18, 10, 19, 9, 21, 8, 24, 7, 27, 6, 30, 5, 33, 4, 36, 3, 45, 2, 55, 1, 74, 1, 75, 19, 10, 20, 9, 22, 8, 25, 7, 28, 6, 31, 5, 34, 4, 37, 3, 46, 2, 56, 1, 76, 4, 38, 3, 47, 2, 57, 1, 77, 4, 39, 3, 48, 2, 58, 1, 78, 5, 35, 4, 40, 3, 49, 2, 59, 1, 79, 4, 41, 3, 50, 2, 60, 1, 80, 6, 32, 5, 36, 4, 42, 3, 51, 2, 61, 1, 81, 4, 43, 3, 52, 2, 62, 1, 82, 7, 29, 6, 33, 5, 37, 4, 44, 3, 53, 2, 63, 1, 83, 4, 45, 3, 54, 2, 64, 1, 84, 8, 26, 7, 30, 6, 34, 5, 38, 4, 46, 3, 55, 2, 65, 1, 85, 4, 47, 3, 56, 2, 66, 1, 86, 9, 23, 8, 27, 7, 31, 6, 35, 5, 39, 4, 48, 3, 57, 2, 67, 1, 87, 3, 58, 2, 68, 1, 88, 10, 21, 9, 24, 8, 28, 7, 32, 6, 36, 5, 40, 4, 49, 3, 59, 2, 69, 1, 89, 2, 70, 1.
This data describes a conspicuous void that in Figure 8.1 resembles a marlin, but when shown compressed horizontally in a large-scale plot, resembles sailboats.
The lengths ℓ pertaining to the subsequences t(N) for 73 ≤ N ≤ 89 are as follows:
37, 2, 21, 8, 8, 10, 8, 12, 8, 14, 8, 16, 8, 18, 6, 20, 4
We recall s(k2..(k2+1)−1) = s(73..89):
10, 1, 19, 4, 4, 5, 4, 6, 4, 7, 4, 8, 4, 9, 3, 10, 2
We compare 2 × s(73..89) to ℓ(73..89) above:
20, 2, 38, 8, 8, 10, 8, 12, 8, 14, 8, 16, 8, 18, 6, 20, 4
Therefore, it seems that the subsequence lengths ℓ(N) = 2 × s(N..(N+1)−1) for Rh(K) + 3 ≤ N < Rh(K+1) and N = Rh(K) + 1. The first subsequence of supersequence K has length ℓ(Rh(K)) = 2 × s(Rh(K)+2) + 1, while ℓ(Rh(K)+2) = 2 × s(Rh(K)) + 1. This is true for 1 ≤ K ≤ 345, given 220 terms of s. If true, then the lengths of subsequences and supersequences can be determined by the terms in the partition of s by indices k2 of second appearances of m, that is, the secondary subsequences of s. The notion is supported by other relationships between second appearances of m and the supersequences and herringbone numbers.
Figure 8.1 manifests the occasion of duplicated h = 10 after t(k2(10)) = t(73). We see two odd ℓ, ℓ(73) = 37, and ℓ(75) = 21 = 2h + 1, separated by ℓ(74) = 2. After we see the last manifestation of the smaller odd length, in t(N) with 76 ≤ N ≤ 89, we have a wide gulf between the “high” and “low” m after the records that start each subsequence. These M approach one another as N increases by 2, separated by increasingly brief subsequences, until we have the beginning of new supersequence.
Table 8.1 lists the index K of the duplicated h = K, followed by index H of subsequence t(H) in which h(K) is found. Rh(K) is the index of the first term s(Rh(K)) of the particular t(i) whose terms are {K, h(K), h(K), …, 1}. Q represents the number of instances of h(K) that appear in t(i). For the entire table click here.
K H R_h Q
--------------------
1 1 1 3
2 9 21 4
3 14 44 5
4 19 75 6
5 28 133 6
6 35 192 7
7 42 261 8
8 55 383 8
9 64 490 9
10 73 609 10
11 90 817 10
12 101 984 11
13 105 1058 11
14 109 1136 11
15 115 1248 11
16 119 1334 11
...
Let h(K) be the K-th instance of duplicated h = K, and let Rh(K) be the index Ri(i) that is the first term of subsequence t(i) such that s(k) = i, s(k+1) = c(i) = h. Example: h(2) = 2 and appears in t(9) starting with s(21) = 9. We see that in t(9) = {9, 2, 2, 3, 2, 4, 2, 5, 1}, we have Q = 4 copies of h(2) = 2.
Subsequence t(Rh(K)) has s(k, k+1, k+2) = {K, h(K), h(K)} where s(k+1) = h(K) corresponds to extant m ⇒ c(m) = 1. In other words, the appearance of h(K) is indeed a consequence of the reflection of the second appearance of record R(K) via Condition 0.
Table 8.2 represents the first differences ℓ of indices of records Ri in s, which are tantamount to the lengths of subsequences t(i), partitioned by those i that harbor herringbone numbers h(K):
J
K 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
--------------------------------------------------------------
1 3 2 2 3 2 3 2 3
2 9 2 5 2 5
3 13 2 7 2 7
4 17 2 9 4 4 6 4 8 4
5 19 2 11 2 11 10 4
6 23 2 13 2 13 12 4
7 27 2 15 6 6 8 6 10 6 12 6 14 4
8 29 2 17 2 17 14 6 16 4
9 33 2 19 2 19 16 6 18 4
10 37 2 21 8 8 10 8 12 8 14 8 16 8 18 6 20 4
11 39 2 23 2 23 18 8 20 6 22 4
12 43 2 25 4
...
The herringbone subsequence t(Rh(K)) is followed by L−1 subsequences t(Rh(K) + J) before the next herringbone subsequence t(Rh(K+1)). Therefore we may speak of a length L of a supersequence T(K), that is, the first differences of the sequence of subsequence indices Rh(K) that denote the presence of a herringbone number h(K). Table A1 contains the first 345 terms of the sequence L, that is, the numbers by which we partition first differences ℓ of indices of records Ri in s. It is evident that apart from the first 2 terms, L = ℓ2, the lengths of s partitioned by the indices k2 of the second occasion of m.
Odd subsequence lengths within supersequences.
We see subsequence t(Rh(K)+1) has ℓ = 2, since t(Rh(K)+1) has s(k, k+1) = {K+1, 1} where s(k+1) = 1, as 1 follows the second occasion of record R, and s(k+1) = 1 is the fruit of Condition 1 and is recalled from an earlier m.
Further, t(Rh(K)+2) has ℓ = (2K + 1) for K > 1, while odd ℓ(Rh(K)) > ℓ(Rh(K)+2). For K > 1, subsequences t(Rh(K) …Rh(K+1)−1) have 2 distinct odd ℓ, the rest are even (there is 1 odd ℓ for K = 1). At times, ℓ(Rh(K)+4) = ℓ(Rh(K)+2) = (2K + 1).
The K < 346 that have ℓ(Rh(K)+4) = ℓ(Rh(K)+2) = (2K + 1) are as follows:
1, 2, 3, 5, 6, 8, 9, 11, 19, 20, 24, 25, 29, 41, 42, 48, 49, 55, 71, 72, 80, 83, 86, 91, 94, 101, 104, 122, 123, 133, 134, 144, 153, 156, 178, 179, 191, 192, 204, 215, 218, 244, 245, 259, 264, 269, 276, 281, 290, 295, 306, 311, 324, 327, ...
Figure 9.1: Scatterplot of supersequence T(42) = t(429..447) = s(9762..10444). This supersequences has two occasions of ℓ = (2K + 1).
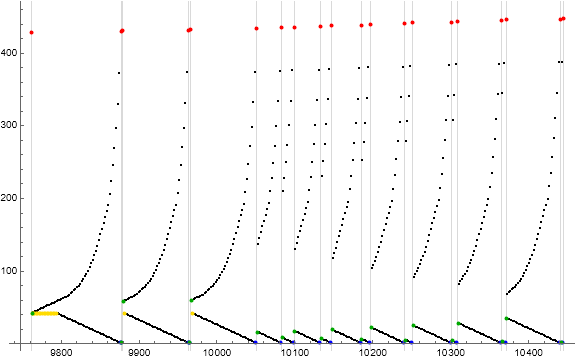
The subsequence lengths ℓ(429..447) are as follows:
115, 2, 85, 2, 85, 32, 16, 34, 14, 38, 12, 44, 10, 50, 8, 56, 6, 70, 4
Compare this to 2 × s(429..447) to ℓ(429..447) above:
84, 2, 116, 2, 118, 32, 16, 34, 14, 38, 12, 44, 10, 50, 8, 56, 6, 70, 4
Therefore if the assertion relating ℓ(n) with 2 s(n) above is correct, then we might also predict the occasion of duplicated smaller odd lengths in supersequences.
Now since h = K, we may also rewrite ℓ(Rh(K)+4) = ℓ(Rh(K)+2) = (2K + 1) as ℓ(Rh(h)+4) = ℓ(Rh(h)+2) = (2h + 1). This means that the above is a list of duplicated h at t(i) that have t(i+2) and t(i+4) with the same odd length.
Table 9.1 regarding supersequence T(K), showing the number of subsequences t(i) in T(K), the number “Dℓ” of distinct lengths ℓ, and the number “Oℓ” of distinct odd lengths. “B” represents (odd) ℓ of the first subsequence t(K, 0) in T(K), while “A” represents a second odd ℓ of t(K, 2) and for the K in the list above, also at t(K, 4). See the full table here.
K R_h(K) Dl Ol A B C D C/D
-----------------------------------------------
1 20 2 1 3 - 1
2 23 3 2 5 9 2 4 0.5
3 31 3 2 7 13 3 6 0.5
4 58 6 2 9 17 4 8 0.5
5 59 5 2 11 19 5 9 0.555556
6 69 5 2 13 23 6 11 0.545455
7 122 9 2 15 27 7 13 0.538462
8 107 7 2 17 29 8 14 0.571429
9 119 7 2 19 33 9 16 0.5625
10 208 12 2 21 37 10 18 0.555556
11 167 9 2 23 39 11 19 0.578947
12 74 4 2 25 43 12 21 0.571429
...
The occasion of {h, h} delimits the “upper end” of a sail shape in the scatterplot, where the bisections of the subsequences converge until the next herringbone number h' = (h+1) duplicates in s. Therefore the action of cardinalities and the arising of herringbone numbers h in their turn produce the characteristic “sailboat” shape of voids in the scatterplot.
Summary.
- The sequence s is infinite; all nonnegative integers m are repeated infinitely.
- The cardinalities of m ≥ 1 grade from 1 down to h in a “hyperbolic” manner, then from h down to R in a gentle manner.
- Records are the natural numberss. Let R < R' be adjacent records: R' = R + 1 for all R, since records R > 0 are the result of Condition 1, a cardinality function. The only novel m in the sequence are its records.
- The minimum of the sequence is 1.
- The appearance of the commonest term M instigates a record in s: 1 ⇒ c(1) = R.
- Occasions of the Condition 0 algorithm m → s(m) report all terms m in s in order, later in the sequence. Hence all terms m are restated in s. Since the restatements or reflections of m = s(k) appear at s(n) for n > k, there are infinite reflections of m in s.
- The sequence s can be divided into finite subsequences t(i) with at least 1 instance of Condition 1 follows Condition 0.
- Subsequences begin with s(k) = i and end with the commonest M = 1.
- The Condition 1 recursion in the coda of the subsequence proceeds from some value m toward 1 and toward a record in a manner that intercalates terms in these bifurcated processes. Hence the run of Condition 1 is finite and the subsequence t(i) has length 2 ≤ ℓ < ∞. As a consequence, there are infinite occasions of Condition 0 through the reporting of c(M) = R, and infinite records that recreate the sequence of nonnegative integers.
- If s(i) = 1, ℓi = 2.
- The scatterplot exhibits trajectories associated with m ⇒ c(m) such that m > 0 have cardinalities that are nonincreasing as m increases toward the record r. Therefore the scatterplot has trajectories that do not cross.
- Let a1 be terms s(k+ℓ−j) in subsequence t(i) with odd 1 ≤ j ≤ ℓ and let a2 have even j. We note that s(k+0) = (i − 1), s(k+1) = s(i), s(k+2) = c(s(i)), etc., and for i > 2, s(k+ℓ−1) = 1. The terms a1(j/2) begin with 1 and usually increase to 2, 3, 4, etc., while the terms a2((j−1)/2) are much larger, falling from a record a2(0) = s(k) that is the first term of the subsequence t(i+1).
- There are cases of duplicated terms h that derive from the Condition 0 recall triggered by the second appearance of m in s. In this case, we have the subsequence R → s(R) ⇒ h ⇒ h ⇒ (h + 1) ⇒ … with Q copies of h. This pattern has h nondecreasing as i increases, but h ≠ 2 and h ≠ 3, and Q nondecreasing at a slower rate. The term h can be repeated only twice adjacently. This is the extreme case of No. 9 above.
- The “sailboat” sequence is so-named for the conspicuous voids that open up at a particular subsequence t(i) then gradually narrow as i increases to a subsequence that has duplicated h. The voids affect the trajectories, causing them to increase and moderate to produce a “scallop” over each sailboat.
- The sequence can be partitioned into subsequences t(i) based on the occasion of records (and Condition 0), and supersequences T(K) based on the occasion of duplicated h = K.
- There are interesting and possibly self-referential resonant lengths of t(i) within the supersequences.
- Odd ℓ are limited to two distinct terms, the smaller, ℓ = 2h + 1, appears in t(i+2) in supersequence T(K).
- Compare this sequence to The Sailboat Sequence.
This concludes our examination.
Appendix:
Table A1: List of lengths L of supersequences T(K):
8, 5, 5, 9, 7, 7, 13, 9, 9, 17, 11, 4, 4, 6, 4, 8, 4, 19, 13, 13, 10, 4, 23, 15, 15, 12, 4, 27, 17, 6, 6, 8, 6, 10, 6, 12, 6, 14, 4, 29, 19, 19, 14, 6, 16, 4, 33, 21, 21, 16, 6, 18, 4, 37, 23, 8, 8, 10, 8, 12, 8, 14, 8, 16, 8, 18, 6, 20, 4, 39, 25, 25, 18, 8, 20, 6, 22, 4, 43, 27, 4, 45, 29, 4, 47, 31, 6, 24, 4, 49, 33, 4, 51, 35, 8, 22, 6, 26, 4, 53, 37, 4, 55, 39, 10, 10, 12, 10, 14, 10, 16, 10, 18, 10, 20, 8, 24, 6, 28, 4, 57, 41, 41, 20, 10, 22, 8, 26, 6, 30, 4, 61, 43, 43, 22, 10, 24, 8, 28, 6, 32, 4, 65, 45, 10, 26, 8, 30, 6, 34, 4, 67, 47, 4, 69, 49, 12, 12, 14, 12, 16, 12, 18, 12, 20, 12, 22, 12, 24, 10, 28, 8, 32, 6, 36, 4, 71, 51, 51, 24, 12, 26, 10, 30, 8, 34, 6, 38, 4, 75, 53, 53, 26, 12, 28, 10, 32, 8, 36, 6, 40, 4, 79, 55, 12, 30, 10, 34, 8, 38, 6, 42, 4, 81, 57, 4, 83, 59, 14, 14, 16, 14, 18, 14, 20, 14, 22, 14, 24, 14, 26, 14, 28, 12, 32, 10, 36, 8, 40, 6, 44, 4, 85, 61, 61, 28, 14, 30, 12, 34, 10, 38, 8, 42, 6, 46, 4, 89, 63, 6, 48, 4, 91, 65, 6, 50, 4, 93, 67, 8, 44, 6, 52, 4, 95, 69, 6, 54, 4, 97, 71, 10, 40, 8, 46, 6, 56, 4, 99, 73, 6, 58, 4, 101, 75, 12, 36, 10, 42, 8, 48, 6, 60, 4, 103, 77, 6, 62, 4, 105, 79, 14, 32, 12, 38, 10, 44, 8, 50, 6, 64, 4, 107, 81, 4, 109, 83, 16, 16, 18, 16, 20, 16, 22, 16, 24, 16, 26, 16, 28, 16, 30, 14, 34, ...
Block[{a = {1}, c, s = {}},
Do[If[IntegerQ@ c[#],
AppendTo[a, c[#]]; c[#]++; Set[s, Rest@ s],
AppendTo[a, a[[#]]]; Set[c[#], 1]] &@ a[[-1]];
Set[s, Insert[s, a[[-2]], LengthWhile[s, # < a[[-2]] &] + 1]], 120]; a]
Document Revision Record.
2021 0706 1645 Final.